Omnidirectional photonic band gap based on nonlinear periodic and quasi-periodic photonic crystals

Abstract

In this paper, we report the effect of the nonlinearity independently of the incident angle $\theta _{0}$ on the reflection properties of 1D periodic and quasi-periodic photonic crystals of type H(LH)${}^{15\ }$and “F${}_{6}$F${}_{6}$F${}_{4}$”, respectively. Which is composed of linear (H layers) and nonlinear (L layers) materials. The linear and nonlinear reflection spectra for both TE and TM polarizations are graphically illustrated using a numerical approach based on the Transfer Matrix Method (TMM). It is shown that the position and the width of the PBG can be controlled by the variation of the electric field intensity (Kerr effect), independently of $\theta _{0}$. Those systems exhibit an Omnidirectional Photonic Band Gap OPBG for any polarization for a common limit $\theta _{0} \in \left[ 0,64{}^\circ \right]$. The most suitable system to have a larger OPBG is the system “F${}_{6}$F${}_{6}$F${}_{4}$” using ZnSe as H layers and Poly-9BCMU as L layers. Our nonlinear models are suitable to be used as good reflectors as well in designing nonlinear optical devices as optical limiting and all-optical switching.

1 Introduction

Propagation of electromagnetic waves through the photonic crystals (PCs) is not restricted to periodic structure, but also includes quasi-periodic structures, such as Fibonacci [1], Thue-Morse [2], Cantor [3], and Octonacci [4, 5] multilayers. This type of PCs can be considered by a simple deterministic generation. Quasi-Periodic Crystals (QPCs) can generate various Photonic Band Gaps (PBGs) in which the propagation of electromagnetic waves is prohibited and corresponds to 100% of reflection similar to the periodic photonic systems. The simplest form of photonic crystal is the one-dimensional photonic crystal (1DPC). For the reason of the properties of PBGs, PCs can be used to develop many optoelectronic devices (optical filters, omnidirectional mirrors, optical diode, optical switches, sensors, etc.) [6,7,8,9], which are utilized in various industries [10, 11], including optical communication and telecommunication networks, where data are transmitted quickly with minimal losses. At any incident angle, the PBGs can be generated in the arbitrary polarization mode (TE and TM) which are called the Omnidirectional Photonic Band Gap (OPBG) [12, 13]. The OPBG has broad applications such as antenna substrates [14] waveguides [15] omnidirectional filters [16], and omnidirectional reflectors [17], etc. For those devices, better performance can be obtained by a wider OBG. Recently, employing nonlinear materials, such as semiconductors, glasses, metals, and polymers, etc. [18], in a PBG material has attracted a big consideration because of particular optical properties. When nonlinearity is integrated into a PC, the light propagation can be controlled dynamically [19, 20], due to the dependence of the refractive index on the intensity (Kerr effect). Kerr nonlinearity holds great importance due to its efficiency in ultra-fast devices. In this regard, 1D nonlinear photonic crystals (1D-NLPCs) which consist of Kerr nonlinear materials have been of specific interest to researchers. They are used in promising applications such as integrated optical devices, optical Schmitt trigger [21], all-optical switching [22, 23], and all-optical diodes [24, 25], etc. The purpose of this paper is to investigate the effect of the nonlinearity (Kerr effect) independently of the incident angle on the optical properties of periodic and quasi-periodic nonlinear PC, which constituted by linear and nonlinear materials. Thus, we will search to find the preeminent OPBG between those structures. Transfer matrix method (TMM) is used to calculate the optical response of the proposed devices. Our paper is organized as follows: We present, in Sect.2, the theoretical formalism employed in this study. Section 3 is devoted to interpret and discuss the obtained results. Conclusions are summarized in the last section.

2 Theoretical model

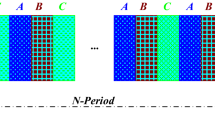
The method used for calculating the optical response (reflectivity) of the different proposed 1D periodic and QPPCs, is the well-known simple and powerful Transfer Matrix Method (TMM). As it is explained in references [26,27,28] and [29] the parameters $r_\mathrm{TE} (r_\mathrm{S})$ and $r_\mathrm{TM} (r_\mathrm{p})$ in TMM that depends on the refractive index for the two polarization TM and TE and for each layer (m) is given by: $r_{\left. m\right| \text {TM}} =\frac{n_{m-1} \cos \theta _{m}-n_{m} \cos \theta _{m-1} }{n_{m-1} \cos \theta _{m} +n_{m} \cos \theta _{m-1} }$, $r_{\left. m\right| \text {TE}} =\frac{n_{m-1} \cos \theta _{m-1} -n_{m} \cos \theta _{m} }{n_{m-1} \cos \theta _{m-1} +n_{m} \cos \theta _{m}}$. In the linear regime, we use the linear refractive index of the material ($n =n^\mathrm{L}$), while in the nonlinear regime ( $n=n^\mathrm{NL}$), we use the expression of the nonlinear refractive index $n^\mathrm{NL} =n^\mathrm{L} \times (1+\mathrm{\chi }^{\left( 3\right) } \times I/2)$ with $I\equiv \left| E\right| ^{2}$ is the intensity of the electric field and $\mathrm{\chi }^{\left( 3\right) }$ being the susceptibility or the Kerr coefficient. The studied periodic 1D-PC under consideration is indicated by H(LH)$^{15}$, and H and L represent, respectively, the layers with high and low refractive index. While, the quasi-periodic 1D-PC is arranged according to the Fibonacci sequence: $F_{n} =F_{n-1} F_{n-2}$ for $F_{1} = \text {L}$ and $F_{2} =\text {LH}$ where $F_{n}$ is the nth generation of Fibonacci structure [30]. Figure 1 shows a schematic of the fourth Fibonacci structure (F${}_{4}$) surrounded by air.

Fig. 1

Structure of the fourth-order 1D-Fibonacci PC

On the one hand, we choose, the TiO$_{2}$ for the linear layers (H layers) and the organic material polydiacetylene 9-BCMU (Poly-9BCMU) for the nonlinear layers (L layers). Their linear refractive indices are, respectively, $n_\mathrm{H} =2.3$ and $n_\mathrm{L} =1.55$. On the other hand, to improve the QP structure, we replace the H layers by the ZnSe with linear refractive index $n_\mathrm{H} =2.63$ and we keep the Poly-9BCMU as the L layers. In the nonlinear regime, it should be noted that for the L layers, we use the expression of the nonlinear refractive index ($n^\mathrm{NL}$). The optical thicknesses of H and L layers were taken by the quarter wavelength condition, i.e., $n_\mathrm{H} d_\mathrm{H} =n_\mathrm{L} d_\mathrm{L} ={\lambda _{0} / 4}$ with $\lambda _{0}$ is the reference wavelength and is taken to be $\lambda _{0} =572~\text {nm}$.

3 Results and discussion

In this work, we try to clarify the following suggestions: What is the most suitable system to have a wider omnidirectional mirror? Up to what limit can we have an omnidirectional mirror with nonlinear systems? And in which field we can use these systems and what are their advantages?

3.1 Structure F$_{6}$F$_{6}$F$_{4}$ using TiO$_{2\ }$and poly-9BCMU materials

The studied structure is a 1D QP multilayered structure built according a combination of blocks of Fibonacci. The system under consideration is “F$_{6}$F$_{6}$F$_{4}$” Where the sixth generation of Fibonacci structure is given by F$_{6}=$“LHLLHLHLLHLLH” and the fourth one is given by F$_{4}=$“LHLLH”. In the next section, we investigate the effect of the incident angle $\theta _{0}$ on the PBG of the structure in linear and nonlinear regime.

3.1.1 Effect of $\theta _{0}$ on PBG in linear regime ($I=0$ MW/cm$^{2}$)

First, it should be noted that all the layers are linear. We start by studying the influence of the incident angle on the reflection in linear regime. In Fig. 2, we represent the 3D reflection spectrum through the structure as a function of the wavelength and the incidence angle for both polarization modes TM and TE.

Fig. 2

Reflection spectrum through the structure F$_{6}$F$_{6}$F$_{4}$ as a function of $\lambda$ and $\theta _{0}$ for both modes TM and TE

Fig. 3

a Width of PBG and b PBG center position, versus $\theta _{0}$ for TE and TM modes

As results, we notice the TE-reflection bandwidth is broader than at normal incidence, whereas the TM-reflection bandwidth is narrower. It is clear that the increase of $\theta _{0}$ induced the shift of the PBG towards shorter wavelengths for the two polarization modes. These results are shown in Fig. 3.

Fig. 4

Variation of the two edges of the PBG as a function of $\theta _{0}$ for the both modes TE and TM

To interpret these results, we represent in Fig. 4 the variation of the edges of the PBG as a function of $\theta _{0}$ for both modes TM and TE. From this figure, we notice that in linear regime, an Omnidirectional Photonic Band Gap (OPBG) is obtained for $\theta _{0} \in \left[ 0,64^\circ \right]$ with a width $\Delta \lambda _\mathrm{OPBG} \; =23.2\times 10^{-3} \mu \text {m}$ covering the wavelength range $[0.67,\mathrm{\; }0.70\mu \text {m}]$. Our aim is to study a nonlinear structure, so we will study the effect of the nonlinearity on the optical response for this structure.

3.1.2 Effect of $\theta _{0}$ on the PBG in nonlinear regime

Before proceeding to the effect of the polarization, we will study the effect of the nonlinearity at normal incident angle.

Effect of electric field intensity on reflection at normal incidence We examine the impact of the electric field intensity on the optical properties of the structure precisely on the PBG. We assume that a Kerr nonlinearity with $\chi ^{\left( 3\right) }\;=\;2.5\;\times \;10^{-5}\text {cm}^{2}/\text {MW}$ is present in all low refractive index layers.

Fig. 5

Linear (solid curve) and nonlinear (dashed curve) reflection spectrum for different input intensities

Fig. 6

Width at middle high of the PBG versus I at normal incidence

We represent in Fig. 5 the reflection spectrum in the linear regime (LR) (solid curve) and in the nonlinear regime (NLR) (dashed curve) for different intensities I. From Fig. 5, we note a displacement of the PBG to the high wavelength by increasing the intensity. In Fig.  6, we represent the variation of the width at middle high of the PBG. By analyzing this figure, we note that by increasing the intensity, the width of the PBG ($\Delta \lambda _\mathrm{PBG}$) decreases exponentially following the equation:

$$\begin{aligned}\Delta \lambda _\mathrm{PBG} \approx 176.7\times 10^{-3} -6.4\; \times 10^{-3} \times \; \exp \left( 18.2\times 10^{-3} \times I\right) .\end{aligned}$$

This result is very important, because we can control the width of the PBG by choosing the intensity of the incident field at normal incident. After this, we will study the effect of the polarization to estimate its effect in nonlinear regime. Effect of the polarization for different intensities We note that the center position of the PBG can be controlled by the variation of the intensity. In Fig. 7, we represent the PBG center position $\lambda _\mathrm{centerPBG}$ versus I for different $\theta _{0}$.

Fig. 7

PBG center position versus I and $\theta _{0}$

The shift of the center of the PBG can be explained using Scalora et al.’s approach [31]. Indeed, for an NLPC with a material exhibiting Kerr nonlinearity, the refractive index value varies by increasing the electric field intensity resulting in a dynamic shift of the band gap. This process is the basis for optical limiting and all-optical switching. In this condition, the optical limiting is reached by changing the incident intensity, while the all-optical switching requires an additional strong pump beam to control the switching of a weak probe signal tuned to the band-gap region [32]. Several researchers [32,33,34] have studied the effect of I in normal incident, but the benefit of the present work is the study of the effect of I independently of $\theta _{0}$. Indeed, we show that the polarization is affected by I.

Fig. 8

Reflection spectrum through the structure F$_{6}$F$_{6}$F$_{4}$ as a function of $\lambda$ and I, for both modes TM and TE and $\theta _{0} =64^\circ$

In fact, the central wavelength $\lambda _{0}$ of the PBGs will blue-shift with the increase of the incident angle $\theta _{0}$. However, the nonlinear effects into the photonic crystal effectively can suppress this blue-shifting. Likewise, to prevent the PBG from moving towards high wavelengths, we can act on $\theta _{0}$ to get this PBG back to its initial position. Now, we study the effect of the intensity on the width of the PBG. For this, we represent in Fig. 8 the reflection spectrum through the structure as a function of the wavelength and the intensity for $\theta _{0} =64^\circ$ and for both polarization modes TM and TE. It is clear that the width of the PBG ($\Delta \lambda _\mathrm{PBG}$) depends upon the intensity. Indeed, it is reduced exponentially for the both modes, as shown in Fig. 9, and may be controlled by the variation of I. Thus, the following expressions were obtained:

In Mode TM:$\Delta \lambda _\mathrm{PBG} \approx 114.1\times 10^{-3} -15.9\; \times 10^{-3} \times \exp \left( 25.8\times 10^{-3} \times I\right)$. In Mode TE:$\Delta \lambda _\mathrm{PBG} \approx 202.1\times 10^{-3} -9.9\; \times 10^{-3} \times \exp \left( 15.8\times 10^{-3} \times I\right)$.

Fig. 9

Width at half-maximum of the PBG versus I, for $\theta _{0} =64^\circ$, for both polarization modes

Fig. 10

Variation of the two edges of the PBG as a function of $\theta _{0}$, for the both modes TE and TM and $I=50$ MW/cm$^{2}$

Then, we note that for the same condition, and for the same range of the incident angle $\theta _{0} =\left[ 0,64^\circ \right]$, the width of the OPBG decreases and it moves from $\Delta \lambda _\mathrm{OPBG} \; =23.2\times 10^{-3} \mu \text {m}$ for the linear regime to $\Delta \lambda _\mathrm{OPBG} \; =21.2\times 10^{-3} \mu \text {m}$ for the nonlinear regime ($I=50$ MW/cm$^{2}$), as shown in Fig. 10. This allows us to say that this decrease in the width of the PBG is due to the increase in the field intensity. Although the nonlinearity has an undesirable effect, we were able to find an OPBG. This result is very important, because in the experimental field, we come across constraints in the choice, of the incident angle of the material which can be nonlinear and the polarization. Our structure shows that we can have an omnidirectional mirror even with a nonlinear material. The OPBG is obtained for low intensities and for different polarization. In the aim to optimize a convenient structure that gives a large OPBG in nonlinear regime, we will study the periodic structure to compare the obtained results to the one last study.

3.2 Periodic structure

To enhance the results, we will modify the structure and we will take a periodic one of type H(LH)$^{15}$ which contains the same number of layers (31 layers). We will study the effect of $\theta _{0}$ in linear and nonlinear regime on the optical properties of this structure. In fact, in linear regime ($I=0$), we represent in Fig. 11 the 3D reflection spectrum through the structure as function of $\lambda$ and $\theta _{0}$ for TM and TE modes.

Fig. 11

The 3D reflection spectrum of H(LH)$^{15}$ structure as a function of $\lambda$ and $\theta _{0}$ for both polarization modes

Fig. 12

Variation of the two edges of the PBG as a function of $\theta _{0}$ for TE and TM modes

As a results, we notice that at normal incidence, we obtain a PBG for the two polarization when $\theta _{0}$ increases. To better interpret these results, we represent the variation of the two edges for the two modes as function as $\theta _{0}$ (Fig. 12).

Now, we proceed to the variation of the electric field intensity (I) to evaluate the effect of the nonlinearity at normal incidence and we consider $\theta _{0} =0$. For this, we represent in Fig. 13 the reflection spectrum through the studied system for different intensities. It has been shown that by increasing of the electric field intensity leads to the shift of the PBG with a switching mechanism occurs. In the same way, the width of the PBG decreases exponentially (Fig. 14).

Fig. 13

Linear (solid curve) and nonlinear (dashed curve) reflection spectrum with different input intensities

Compared to the precedent structure, we can note that the obtained PBG is narrower when I increases such as the previous structure and the PBGs shifts towards higher wavelength when I increases and the opposite for $\theta _{0}$.

Fig. 14

Width at half-maximum of the PBG versus I at normal incidence

Fig. 15

Reflection spectrum of H(LH)$^{15}$ structure as a function of $\lambda$ and I, for TE and TM modes and $\theta _{0} =64^\circ$

To study the effect of the intensity on the width of the PBG, we represent in Fig. 15 the reflection spectrum through the structure as a function of $\lambda$ and I for $\theta _{0} =64^\circ$ and for both polarization modes TM and TE.

Even for this system, $\Delta \lambda _{PBG}$ depends on the intensity independently of $\theta _{0}$ as shown in Fig. 16. Therefore, we can control this width through a determined I using the following equations:

Fig. 16

Width at half-maximum of the PBG versus I, for both polarization modes and $\theta _{0} =64^\circ$

In Mode TM: $\Delta \lambda _\mathrm{PBG} \approx 101.8\times 10^{-3} -0.9\; \times 10^{-3} \times \exp \left( 26.9\times 10^{-3} \times I\right)$. In Mode TE: $\Delta \lambda _{PBG} \approx 180.7\times 10^{-3} -5.5\; \times 10^{-3} \times \exp \left( 21.4\times 10^{-3} \times I\right)$.

Fig. 17

Variation of the two edges of the PBG as a function of $\theta _{0}$, for the both modes TE and TM and $I=50$ MW/cm$^{2}$

Furthermore, for a fixed intensity ($I=50$ MW/cm$^{2}$), we obtain an OPBG for $\theta _{0} \in \left[ 0,64{}^\circ \right]$, as Fig. 17 illustrates, and its width is $\Delta \lambda _\mathrm{OPBG} \; =45.1\times 10^{-3} \mu \text {m}$. It is wider than that of the previous structure. In fact, for the periodic structure, we have the same effect on the group (HL), while for the quasi-periodic structure, we do not have the same group, so the effect changes, i.e., the field in the layers is influenced by the polarization and the refractive index which affects on the multiple reflections inside the system. In the next section, we try to improve the OPBG even more. Therefore, we try to act on the QP structure F$_{6}$F$_{6}$F$_{4}$ by changing the H layers by a material with higher refractive index and keeping the L layers.

3.3 Structure F$_{6}$F$_{6}$F$_{4}$ with the materials ZnSe and poly-9BCMU

In this part, the system under consideration is a Fibonacci structure F$_{6}$F$_{6}$F$_{4}$ using the Zinc Selenide ZnSe for the H layers with a refractive index $n_\mathrm{H} =2.63$ and we keep the Poly-9BCMU for the L layers. In linear regime, we illustrate in Fig. 18 the variation of the two boards of the PBG for both polarization modes.

Fig. 18

Variation of the two edges of the PBG as a function of $\theta _{0}$, for the both modes TE and TM using ZnSe

As results, we notice that at normal incidence, we obtain an OPBG larger than that of the other structures. Its width is equal to: $\Delta \lambda _\mathrm{OPBG} \; =65.6\times 10^{-3} \mu \text {m}$ for $\theta _{0} \in \left[ 0,64{}^\circ \right]$.

Fig. 19

Linear (solid curve) and nonlinear (dashed curve) reflection spectrum with different input intensities

In normal incidence, we represent in Fig. 19 the variation of the reflection for different intensities. As it has been shown, this system presents a wider width of the PBG and it follows this equation: $\; \Delta \lambda _\mathrm{PBG} \approx 221.8\times 10^{-3} -6.7\times 10^{-3} \times \; \exp \left( 18.1\times 10^{-3} \times I\right)$. In nonlinear regime, this system presents an OPBG for $\theta _{0} \in \left[ 0,64^\circ \right]$ (Fig. 20) with a width $\Delta \lambda _\mathrm{OPBG} \; =83.5\times 10^{-3} \mu \text {m}$, which is larger than all the considered previous structures. Therefore, the considered material ZnSe is a good choice to enlarge the OPBG. Given all of the above, the system F${}_{6}$F${}_{6}$F${}_{4}$ using ZnSe as high index layers is the most suitable system to have a larger omnidirectional mirror. The obtained OPBG with nonlinearity systems is for $\theta _{0} \in \left[ 0,64{}^\circ \right]$. These systems have the potential to be used as excellent reflectors for designing nonlinear optical devices like optical limiting and optical switches which can be achieved by a dynamic shift of the PBG through the variation of the intensity. The benefit of this work is the study of the effect of the intensity of the electric field independently of the polarization.

Fig. 20

Variation of the two edges of the PBG as a function of $\theta _{0}$, for the both modes TE and TM and $I=50$ MW/cm$^{2}$

4 Conclusion

In summary, we have studied the effect of nonlinearity and the incident angle on the reflection properties of a periodic and QP-1D PCs using TMM method for the TE and TM polarization. For all the structures, we have noted a dynamically shift in the location of the PBG towards higher wavelengths. This shifting is due to the Kerr effect which leads to the variation of the refractive index of the material in response to the applied electric field intensity. The position and the width of the PBG can be controlled by the variation of I; thus, we can shift the PBG to the desired region independently of the incidence angle. Then, the structure may behave like a switch working in the optical region. In addition, we have shown that those systems present an OPBG for any polarization, which is limited in $\theta _{0} \in \left[ 0,64{}^\circ \right]$. The most suitable system to have a larger omnidirectional mirror is the QP system F${}_{6}$F${}_{6}$F${}_{4}$ using ZnSe as high index layers and Poly-9BCMU as low index layers. This system behaves like a reflector at low or high intensity of controlling wave, at a particular wavelength. In this study as interesting results, we find that our proposed nonlinear models provide many possible applications as good reflectors, as well for designing nonlinear optical devices as all-optical switching and optical limiting devices.