1 Introduction

Femtosecond fiber lasers have gained great research interest due to their low cost, flexibility, and good reliability [1, 2]. For the generation of femtosecond pulses, soliton mode-locking is one of the most frequently used techniques [3,4,5]. Employing soliton mode-locking has certain advantages. First, soliton mode-locking allows for significantly stronger nonlinear phase shift arising from the Kerr nonlinearity, which would otherwise make the pulses unstable. Second, there is no temporal broadening of the pulses nor any change of their spectrum when solitons propagate in fibers due to the balance between dispersions and nonlinearity [6, 7]. Recently, femtosecond fiber lasers also find significant applications in rapidly expanding photon-science facilities, where an ultra-low noise optical master oscillator provides multiple optical signals to be distributed to various clients [8, 9], time distribution through fiber links [10], seedings for coherent beam combining fiber amplifiers [11], and also in multicolor spectroscopy [12, 13]. Feeding synchronized soliton pulses into different channels holds the potential to broaden these applications further.

However, boosting the soliton energy is not easy. For a soliton laser, the pulse energy is essentially fixed or quantized, and therefore, it is incapable to increase soliton energy continuously with stronger pumping [5]. Additional pulses appear within the laser resonator as the pump is increased above a certain level, and the laser output is typically a randomly spaced group of pulses, repeating with a period equal to the resonator round-trip time. This phenomenon is called soliton fission, in which a soliton with high energy (high-order soliton) breaks into several fundamental solitons. Meanwhile, the circulating soliton pulse can shred substantial energies into Kelly sidebands in the spectrum [5, 7, 14]. For these reasons, 100 pJ used to be regarded as the energy limitation of soliton pulses in fiber lasers [15].

To overcome this energy limitation, a series of methods have been developed, including engineering either the dispersion or the gain in the laser resonator to generate the so-called similaritons, dispersion-managed solitons, and dissipative solitons [16,17,18]. By employing the nonlinear polarization evolution (NPE) mode-locking combined with a saturable absorber, it is also possible to generate high-order solitons [19]. All of these methods can push the pulse energy up to the nJ level but also drive the pulse shape away from the hyperbolic secant pulse shape-soliton, as well. However, in applications of synchronization distribution, fundamental solitons have neglectable degradation after long-distance fiber propagation, and an unstretched pulse can also keep the signal-to-noise ratio high [20]. Lasers constructed with polarization-maintaining (PM) fibers are preferred in these applications thanks to their robustness.

In this paper, we propose and implement an all-PM-fiber laser to generate robust higher energy (high-order) solitons free of soliton fission.

2 Laser configuration

As is known, both fundamental solitons and high-order solitons are solutions of the nonlinear Schr\(\ddot{o}\)dinger equation [21]

$$\begin{aligned} \frac{\partial A}{\partial z}+\frac{1}{2}i\beta _2\frac{\partial ^2 A}{\partial t^2}=i\gamma |A|^2A, \end{aligned}$$
(1)

where A is the amplitude of the soliton, \(\beta _2\) is the group velocity dispersion, \(\gamma\) is the nonlinear coefficient, and z and t are coordinates of the retarded frame. A fundamental soliton can propagate in a dispersive medium with a constant shape of the temporal intensity profile, and can be expressed as \(A=A_0sech(t/T_0)e^{-i\beta _2/{2T_0^2}z}\), where \(T_0\) is the pulse duration. A higher order soliton is a soliton pulse with the energy of N times that of a fundamental soliton, and N is called the order of the soliton, which can be introduced using [22]

$$\begin{aligned} N^2=\frac{L_D}{L_{NL}}\equiv \frac{\gamma P_0 {T_0}^2}{|\beta _2|}, \end{aligned}$$
(2)

where \(L_D\) is the dispersion length, \(L_{NL}\) is the nonlinear length, and \(P_0\) is peak power. We can clearly recognize that the order of soliton depends not only on the parameters of the pulse itself, but also on the characteristics of the fibers. In addition to this, the temporal shape of such high-order soliton is different from the fundamental soliton and varies periodically during propagation.

The length of a soliton cycle, also called soliton period, is defined as \(L_{soliton} = \frac{\pi }{2}\frac{T_0^2}{\vert \beta _2 \vert }=\frac{\pi }{2} L_D\). During a soliton period, a high-order soliton will evolve from one peak to multiple peaks and then back into one peak in the time domain. For example, the evolution of a seventh-order soliton within a soliton period is presented in Fig. 1. In reality, the multiple peaks would walk away (soliton fission) due to high-order effects and other perturbations, such as high-order dispersions, intra-pulse Raman effects, and two-photon absorptions [23].

Because of this walking away of soliton fission, they are not suitable for applications mentioned above. However, if one can build a fiber laser oscillator with a short resonator length in which the high-order soliton cannot evolve into multiple peaks, then soliton fissions, caused by these unquenchable perturbations,can be avoided. High-order solitons, fission free, then can be split into multiple fundamental solitons to be used for time synchronization and so on. The fission lengths for solitons are different for different soliton orders. The shortest length that leads to soliton fission, \(L_{fiss}\), and the order of soliton, N, are related as [22]

$$\begin{aligned} L_{fiss}=L_D/N. \end{aligned}$$
(3)

For example, for a seventh-order soliton, \(L_{fiss}=0.09L_{soliton}\). If the length of the laser resonator is shorter than \(L_{fiss}\), shown with a dashed red line in Fig. 1, this soliton can be delivered from the laser before evolving into several peaks and soliton fission will be avoided.

Fig. 1
figure 1

Simulation of the evolution of a seventh-order soliton in one \(L_{soliton}\) only considering group velocity dispersion and self-phase modulation. White dashed line shows the length of the effective laser resonator. Red dashed line shows the \(L_{fiss}\)

Full size image

Although a short resonator can help to prevent soliton fission, the gain is not enough for generating high-order soliton (the gain fiber length will be too short). To resolve this dilemma, we build an effective short resonator laser with a nonlinear amplifying loop mirror (NALM). Like a nonlinear loop mirror, NALM works as an effective end mirror with high reflectance, R, yet with gain fiber in the loop to introduce sufficient gain. Combined with the other end mirror and some other elements, a fiber laser with an effective short resonator length and high gain can be constructed.

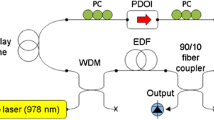
The schematic layout of the proposed laser is shown in Fig. 2, and the fiber length of the linear arm is 28.90 cm. This is the effective evolution length of the high-order soliton, and it is kept smaller than \(L_{fiss}\). Thanks to the high output ratio and the split of the pulse energy at the coupler, the energy of two replicas in the NALM is not high enough to lead to soliton fission. All fibers and fiber components employed here are PM ones. Moreover, both WDMs and couplers are coated types with fast axis blocked too. The total dispersion of the resonator is \(-77280\)fs\(^2\). Different from most NALM lasers, two segments of 0.70 m-long erbium-doped fiber (EDF) (Nufern, PM-ESF-7/125, \(\beta _2 = -23\)fs\(^2\)/mm) are placed symmetrically in the loop for two main purposes. First and foremost, the symmetry of the loop will provide the highest reflectance, which can be expressed as

$$\begin{aligned} R=2\alpha (1-\alpha )(1+cos\Delta \Phi _{NL}), \end{aligned}$$
(4)

where \(\alpha\) is the ratio of the coupler and \(\Delta \Phi _{NL}\) is the nonlinear phase shift difference in the loop between the clockwise and counter-clockwise propagating pulses. Here, \(\alpha\) is chosen to be 0.5 and \(\Delta \Phi _{NL}\) is kept small to reach the maximum of R, which means low loss from the effective NALM and helps to generate high-energy solitons. Employing two segments of gain fiber also provides freedom to further balance \(\Delta \Phi _{NL}\) caused by nonuniform gain distribution in the EDF, subtle differences of fiber components symmetrically inserted inside the loop, and inevitable fiber length mismatch in practice. Besides, small \(\Delta \Phi _{NL}\) is also desirable to maintain the soliton structure of the pulses. In addition, two segments of gain fiber also provide more gain for high-energy solitons.

Fig. 2
figure 2

Schematic of the all-PM-fiber laser. LD laser diode, WDM wavelength division multiplexer, EDF erbium-doped fiber, HWP half-wave plate, PBS polarization beam splitter, SESAM semiconductor saturable absorption mirror

Full size image

3 Results and discussion

The characteristics of the output at the maximum output power are shown in Fig. 3. The spectrum is measured by an optical spectral analyzer (Yokogawa,AQ6370D), which shows a center wavelength at 1554.8 nm with a 3 dB bandwidth of 6.1 nm, shown in Fig. 3a. The spectrum can be fitted very well by a hyperbolic secant pulse with parameters above, confirming a typical soliton mode-locking operation. The autocorrelation (AC) trace of the soliton pulses measured by a commercial autocorrelator (APE,Pulsecheck) is shown in Fig. 3b. The estimated hyperbolic secant pulse duration (full width at half maximum) is 436 fs, and the time–bandwidth product (TBP) is 0.331, close to the transform limited value.

We examined carefully that there is no additional pulse showing up in a scanning range of 15 ps. The oscilloscope trace (Tektronix, DPO70404C) and the RF spectra (Rigol, DSA815) are shown in Fig. 3c and d, where a 50.35 MHz repetition rate is consistent with the real resonator length of \(\sim\) 4.05 m. The RF spectrum over a wide span of 1.5 GHz is also recorded as shown in the top left corner of this figure. All these show clearly the pattern of soliton mode-locking without fissions, even at the highest output pulse energy. To further prove this result, we used the Split-Step Fourier Method (SSFM) to simulate the evolution of the high-order soliton output from NALM in linear arm numerically, and the spectra of the initial evolving pulse are determined by the spectra detected from the taps in the loop mirror. The validity of the simulation is confirmed by comparing the spectra at all these spots of taps, and there is no fission found in our simulation either.

Fig. 3
figure 3

Features of output soliton. a The spectrum of the soliton (red solid line) and \(\hbox {sech}^2\) fitting curve (blue dashed line). b AC trace (red solid line) an \(\hbox {sech}^2\) fitting curve (blue dashed line). c A pulse train of the soliton is measured by an oscilloscope. d RF spectrum of output pulses with a resolution bandwidth (RBW) of 5 kHz and a bandwidth of 2.0 MHz. The inset is the RF spectrum measured with an RBW of 2.5 MHz and a bandwidth of 1.5 GHz

Full size image

To find the optimal output ratio, free space elements including a half-wave plate (HWP) and a polarization beam splitter (PBS) are placed in the laser resonator instead of PM-fiber components. The solitons output from output 1 and output 2 are obtained by incomplete reflection of s-polarized solitons caused by the slight tilt of the PBS to prevent end reflection.

Because two long gain fibers are employed and extra losses are introduced by the reflection of HWP and PBS in the resonator, the pump power threshold of mode-locking is higher than that of a usual laser. The transmittance (T) of the effective end mirror (NALM) reaches the minimum when the pump powers of the two LDs are close to each other. It leads to R at the maximum and \(\Delta \Phi _{NL}\) close to 0, which is consistent with the design idea.

If the HWP is set to a proper angle, the laser will maintain a single-pulse mode-locking operation when the pump powers are above 300 mW. When the pump powers of both LDs are at the maximum (\(\sim\) 750mW), we get maximum output 1 (\(P_{o1}\)) and output 2 (\(P_{o2}\)) at 60.10 mW and 13.54 mW, respectively. The corresponding single pulse energies are 1.19 nJ and 0.27 nJ, respectively. Notably, even the lower energy of this laser is over two times of conventional soliton laser energy. Linear relationships between output powers and pump powers are illustrated in Fig. 4, for both output 1 and output 2. It shows a large power tuning range.

With the maximum pump power, the maximum intracavity pulse energy is 4.47 nJ, which is calculated from the output power of the taps in the loop. Meanwhile, in our experiment, \(T_0\) = 436fs/1.543 = 282.57fs (\(\hbox {Sech}^2\) Fitting), \(\gamma\) = 0.002\(\hbox {W}^{-1}\hbox {m}^{-1}\), and \(P_0\) = \(E_0\)/\((2T_0)\) = 7.91kW, so we can calculate that the order of soliton N = 7.41 \(\approx\) 7, according to Eq.(2). With a higher pump power, the soliton energy can be further increased. For our laser, \(L_{soliton}\) = 4.18 m and \(L_D\) = 2.66 m. The effective resonator length is 28.9 cm, about 0.07\(L_{soliton}\) (shown with the white dashed line in Fig. 1). Ideally, the laser resonator can support up to the ninth-order soliton without fission, corresponding to a soliton with an energy of 7.39 nJ and almost 1.5 times more than the output energy obtained here.

Fig. 4
figure 4

Continuously varying pump power of LD1 at three different fixed pump power of LD2 (462 mW, 525 mW, and 584 mW correspond to yellow, red, and blue marks, respectively) to investigate laser output characteristics. The fittings of \(P_{o1}\) are represented by solid lines, and those of \(P_{o2}\) are represented by dashed lines

Full size image

The working conditions of this laser are sensitive and greatly influenced by the energy output efficiency from the resonator, which is directly controlled by HWP here. Therefore, choosing an appropriate ratio of the fiber coupler is important for integration. The effect of output coupling efficiency on the laser operation statuses is studied by angle-tuning the HWP relative to the horizontal polarization axis with angle \(\theta\), which is shown in Fig. 5. For different ranges of the coupling efficiency, the ratio between laser powers outputted from output 1 and from the loop mirror, \(\frac{P_{o1}}{P_1}\), the laser works in three different statuses: single-pulse mode-locking, unstable mode-locking (soliton fission or multiple-pulse operation), and non-mode-locking operation. For single-pulse mode-locking, the HWP angle is constrained by \(\delta\), the ratio between \(P_2\) and \(P_1\), where \(P_2\) is the pulse power injecting into loop mirror (P1 and P2 can be calculated from the output of two 2x2 tap couplers with known transmission ratios in the loop), and the laser intensity on the SESAM, \(16^\circ<\theta <20^\circ\). Those two parameters limit the maximum and the minimum coupling efficiency, respectively. Higher output coupling efficiency than this range contributes to smaller power reflected back to the loop mirror, making the laser unable to oscillate. And lower output coupling efficiency leads to higher laser intensity on the SESAM, making the laser fall into multiple-pulse operation. Besides, the range of HWP angle for single-pulse mode-locking is wider under lower pump power conditions. Only the minimum coupling efficiency decreases, while the maximum holds, since lower pump power leads to reduced laser intensity on the SESAM. Therefore, people can enhance the robustness against the output coupling efficiency by sacrifying the output pulse energy. To enhance the stability, one can replace the spatial ’coupler’ (the HWP and the PBS) with a fiber coupler. The coupling ratios can be determined with the restriction on \(\delta =\frac{P_2}{P_1}>3\%\), to shift away from non-mode-locking operation. Therefore, a fiber coupler with a coupling ratio of 80:20 \(2 \times 2\) can be chosen to build a more robust all-fiber-structure laser.

Fig. 5
figure 5

The working conditions’ transformation with the change of the HWP angle \(\theta\). Single-pulse mode-locking, non-mode-locking, and unstable mode-locking (soliton fission or harmonic mode-locking) are marked by blue square, yellow circle, and green triangle marks, respectively. The condition range of single-pulse mode-locking is \(\pm 2^{\circ }\) around optimum working points (\(18^{\circ },-27^{\circ }\) and \(63^{\circ }\)). The \(cos^2\) fitting (red dashed line) reflects Malus law. Because of the slight tilt of the PBS, the maximum of the fitting line is much less than 1

Full size image

4 Conclusion

In conclusion, by employing an NALM and an end mirror (SESAM, in our case) to make an effective short laser resonator, we realize a self-starting, stably operating high-energy soliton laser, free of soliton fission. To obtain a high reflection from the NALM and high gain, we have two segments gain fibers placed symmetrically in the NALM, which also provides more freedom to balance the gain in the loop. Notably, This method does not depend on the doping type of gain fibers. In the reported laser based on EDF, a seventh-order soliton with an estimated energy of 4.47 nJ is able to stably oscillate in the laser resonator without fission, and output solitons with energy up to 1.19 nJ are obtained. The high-order soliton without fission of the reported laser is in good agreement with the theoretical prediction. Ideally, the reported laser resonator can tolerate up to ninth-order soliton without fission and will provide an output soliton energy exceeding 1.97 nJ.

Even though the operating condition of the laser is sensitive to the output ratio, stable mode-locking with a large power tuning range still can be obtained once the output ratio is set properly. A more robust and more convenient all-fiber structure will be possible by replacing the HWP and PBS with a fiber coupler to maximize the advantages of all-PM-fiber lasers. It may also further increase the output energy due to the reduced loss in the resonator. In addition, \(2 \times 2\) couplers are preferable to make full use of the energy of the laser. Based on such a universal method, a laser capable of outputting high-order soliton, adjustable output energy, and with multiple output ports will have great application prospects in the field where multiple synchronized soliton pulses are desired, including multichannel synchronization signal distributions.