1 Introduction

With the arrival of the era of big data, a large amount of data needs to be stored for a long time. The holography is regarded as a good candidate, because it has the advantages of high speed, high density, low cost, and long storage time [1,2,3]. The conventional holography only records the amplitude and phase of optical wave, and yet the polarization is not employed. Hence, the polarization holography that records all the information of optical wave is proposed, and its data storage density is larger than the conventional holography [4,5,6]. Moreover, the polarization holography may be applied in another field besides the data storage. Since the polarization state of reconstructed wave can be controlled in polarization holography, it may be used as micro nano processing technology [7]. For example, the polarizer that generates the circularly polarized wave with arbitrary polarized incident wave may be fabricated by polarization holography [8]. In addition, the polarization holography can produce the vector beam and vortex beam conveniently [9,10,11]. Thus, the key advantage of polarization holography over conventional holography is that it can manipulate the polarization state of reconstructed wave freely.

Under the paraxial condition, the theory based on Jones matrix can well describe the polarization state of reconstructed wave in polarization holography [12, 13]. However, the paraxial condition means that the angle between the signal and reference waves is less than 10°, and it limits the application of polarization holography, because the aforementioned angle in conventional holography is arbitrary. To break through the limitation of paraxial approximation, a new polarization holography theory based on the tensor method is proposed, which could explain the experimental result with arbitrary angle between the signal and reference waves [14].

In general, the polarization state of reconstructed wave can be expressed as

$${\mathbf{G}}_{{\mathbf{F}}} \propto \alpha {\mathbf{G}}_{ + } + \beta {\mathbf{G}}_{ + }^{\prime } ,$$
(1)

where GF represents the reconstructed wave, G+ represents the signal wave, G+′ is the orthogonal polarization state of signal wave, α and β are the corresponding coefficients. Equation (1) implies that the polarization state of reconstructed wave can be manipulated by taking different values of α and β. When β is 0, it means that the faithful reconstruction is achieved [15]. The faithful reconstruction, the polarization state of reconstructed wave being identical to that of signal wave, is the basis of data storage and image display [16, 17]. When α and β are equal to 0 simultaneously, the reconstructed wave would vanish, and it is the null reconstruction [18,19,20]. α being 0 implies that the polarization state of reconstructed wave is orthogonal to that of signal wave, and it is called the orthogonal reconstruction that will be studied in this work. So far, there are few reports about the case α = 0. In contrast, there have been many reports on the other two cases [21]. The lack of orthogonal reconstruction may be a flaw of tensor polarization holography theory.

Thus, in this work, we deduce the conditions for achieving the orthogonal reconstruction in polarization holography, where the polarization state of signal wave is orthogonal to that of reference wave. Under the circumstances, the reconstruction character of polarization holography can be exhibited fully. To get a universal result, we choose the elliptically polarized wave in the experiment, because both linearly polarized wave and circularly polarized wave may be regarded as its special cases. Then, we design the experiment and observe the orthogonal reconstruction when the angle between the signal and reference waves is obtuse. The experimental results are consistent with our expectations. The experimental results prove the correctness of theoretical analysis. In addition, it may be concluded that the angle between the signal and reference waves is the key to observe the orthogonal reconstruction.

2 Theory

Figure 1 shows the recording and reconstructing stages of polarization holography, where G– represents the reference wave, F is the reading wave, θ+ and θ- are the incident angles of signal and reference waves. The reconstructed wave based on the tensor polarization holography theory and coupled wave theory can be expressed as [14]

$${\mathbf{G}}_{{\mathbf{F}}} \propto B{\mathbf{(G}}_{ - }^{{\mathbf{*}}} \cdot {\mathbf{F)G}}_{ + } + A{\mathbf{(G}}_{ + } \cdot {\mathbf{G}}_{ - }^{{\mathbf{*}}} {\mathbf{)F}} + B{\mathbf{(G}}_{ + } \cdot {\mathbf{F)G}}_{ - }^{{\mathbf{*}}} - \left\{ {[A{\mathbf{(G}}_{ + } \cdot {\mathbf{G}}_{ - }^{{\mathbf{*}}} {\mathbf{)F}} + B{\mathbf{(G}}_{ + } \cdot {\mathbf{F)G}}_{ - }^{{\mathbf{*}}} ] \cdot {\mathbf{k}}_{ + } } \right\}{\mathbf{k}}_{ + } ,$$
(2)
$${\mathbf{k}}_{ + } = \left( {\begin{array}{*{20}c} { - \sin \theta_{ + } } \\ 0 \\ {\cos \theta_{ + } } \\ \end{array} } \right).$$
(3)
Fig. 1
figure 1

Schematic diagram of polarization holography. a Recording stage; b reconstructing stage

Full size image

In Eq. (2), A and B are coefficients of the scalar and tensor components of the photo-induced change in the dielectric tensor, and referred to the coefficients for intensity and polarization holograms, respectively. k+ is the wave vector of signal wave, and the superscript * indicates conjugate. In general case, the signal, reference, and reading waves can be expressed as

$${\mathbf{G}}_{ + } \propto a{\mathbf{s}} + be^{i\varphi } {\mathbf{p}}_{ + } ,$$
(4)
$${\mathbf{G}}_{ - } \propto c{\mathbf{s}} + de^{i\delta } {\mathbf{p}}_{ - } ,$$
(5)
$${\mathbf{F}} \propto m{\mathbf{s}} + ne^{i\psi } {\mathbf{p}}_{ - } ,$$
(6)
$${\mathbf{s}}{ = }\left( {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right),{\mathbf{p}}_{j} { = }\left( {\begin{array}{*{20}c} {\cos \theta_{j} } \\ 0 \\ {\sin \theta_{j} } \\ \end{array} } \right),$$
(7)

where s and pj are the unit vector of the s- component and p- component, respectively. The subscripts j =  + or  −represent the signal wave and the reference wave, respectively. a, b, c, d, m, and n represent the amplitude of s-component and p-component of corresponding waves. φ, δ, and ψ denote the phase difference between s- and p-components. Inserting Eqs. (3)–(7) into Eq. (2) gives

$$\begin{gathered} {\mathbf{G}}_{{\mathbf{F}}} \propto {\mathbf{G}}_{ + } \left\{ {B\left( {a^{2} + b^{2} } \right)\left[ {cm + dne^{{i\left( {\psi - \delta } \right)}} } \right] + A\left[ {ac + bde^{{i\left( {\varphi - \delta } \right)}} \cos \theta } \right]\left[ {am + bne^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right]} \right. \hfill \\ \left. {\quad \quad + B\left[ {am + bne^{{i\left( {\varphi + \psi } \right)}} \cos \theta } \right]\left[ {ac + bde^{{ - i\left( {\varphi + \delta } \right)}} \cos \theta } \right]} \right\} \hfill \\ \quad \quad + {\mathbf{G}}_{ + }^{\prime } \left\{ {A\left[ {ac + bde^{{i\left( {\varphi - \delta } \right)}} \cos \theta } \right]\left[ {bm - ane^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right] + B\left[ {am + bne^{{i\left( {\varphi + \psi } \right)}} \cos \theta } \right]\left[ {bc - ade^{{ - i\left( {\varphi + \delta } \right)}} \cos \theta } \right]} \right\}, \hfill \\ \end{gathered}$$
(8)

where θ = θ+  + θ–, which is the angle between the signal and reference waves inside the recording material.

When two arbitrarily polarized waves are orthogonal, they can be expressed as

$${\mathbf{G}}_{1} \propto v{\mathbf{s}} + ue^{{i\gamma_{1} }} {\mathbf{p}},$$
(9)
$${\mathbf{G}}_{2} \propto u{\mathbf{s}} + ve^{{i(\gamma_{1} + \pi/2)}} {\mathbf{p}},$$
(10)

Obviously, Equation G1·G2* = 0 is the sufficient and necessary condition about the two orthogonal polarization states. In Fig. 2, we plot the polarization state of G1 and G2, where γ1 represents the phase difference between p- component and s- component of the wave G1. Thus, for the wave G2, the aforementioned angle is γ1 + π/2. As shown in Fig. 2, G1 and G2 have the different rotation direction.

Fig. 2
figure 2

Schematic diagram of orthogonal polarization state

Full size image

In the experiment, what we consider is the case that the polarization state of signal wave is orthogonal to that of reference wave in the recording stage. It means d = a, c = b, δ = φ + π. Then, Eqs. (5) and (8) can be expressed as

$${\mathbf{G}}_{ - } \propto b{\mathbf{s}} - ae^{i\varphi } {\mathbf{p}}_{ - } ,$$
(11)
$$\begin{gathered} {\mathbf{G}}_{{\mathbf{F}}} \propto {\mathbf{G}}_{ + } \left\{ {B\left( {a^{2} + b^{2} } \right)\left[ {bm - ane^{{i\left( {\psi - \varphi } \right)}} } \right] + Aab\left( {1 - \cos \theta } \right)\left[ {am + bne^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right] + Bab\left[ {am + bne^{{i\left( {\varphi + \psi } \right)}} \cos \theta } \right]\left( {1 - e^{ - 2i\varphi } \cos \theta } \right)} \right\} \hfill \\ \quad \quad + {\mathbf{G}}_{ + }^{\prime } \left\{ {Aab\left( {1 - \cos \theta } \right)\left[ {bm - ane^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right] + B\left[ {am + bne^{{i\left( {\varphi + \psi } \right)}} \cos \theta } \right]\left( {b^{2} + a^{2} e^{ - 2i\varphi } \cos \theta } \right)} \right\}. \hfill \\ \end{gathered}$$
(12)

Obviously, Eq. (12) confirms the validity of Eq. (1), because the polarization states of signal, reference, and reading waves are assumed to the elliptically polarized and the result is universal. In Eq. (12), the orthogonal reconstruction will be achieved when the coefficient of G+ equals zero. This condition yields

$$\frac{A}{B}{ = } - \frac{{\left( {a^{2} + b^{2} } \right)\left[ {bm - ane^{{i\left( {\psi - \varphi } \right)}} } \right]}}{{ab\left( {1 - \cos \theta } \right)\left[ {am + bne^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right]}} - \frac{{\left( {1 - e^{ - 2i\varphi } \cos \theta } \right)\left[ {am + bne^{{i\left( {\varphi + \psi } \right)}} \cos \theta } \right]}}{{\left( {1 - \cos \theta } \right)\left[ {am + bne^{{i\left( {\psi - \varphi } \right)}} \cos \theta } \right]}},$$
(13)

where the ratio of A to B changes with the exposure time [22]. Since the signal and reference waves are given, we may choose the suitable m, n, and ψ to satisfy Eq. (13).

In the experiment, the phenanthrenequinone-doped polymethyl methacrylate (PQ/PMMA) is used as the recording material. The previous study shows that the initial A/B value is around 8 [23]. For orthogonal reconstruction, we may calculate m, n, and ψ from Eq. (13). Then, by these calculated m, n, and ψ values, we may get the coefficient of G+′ from Eq. (8). In Fig. 3, we plot the coefficient of G+′ as well as m/n value varying with the angle between the signal and reference waves, where A/B = 8, a = 20.5, b = 1, and φ = ψ = π/2. We would like to note that φ = ψ = π/2 means the major or minor axis of ellipse describing the electrical field of signal, reference, and reading waves is along the horizontal direction.

Fig. 3
figure 3

Coefficient of G+′ and m/n value varying with recording angle

Full size image

From Fig. 3, we can see that when the recording angle is less than 90°, the coefficients are close to or even less than 0. When the coefficient is close to 0, it means that the power of the reconstructed wave is very low and can be treated as the null reconstruction [19]. When the coefficient is less than 0, it may indicate a π phase shift. However, in the experiment, the measured parameter is power, thus the amplitude coefficient being less than 0 will not affect our experimental result. In contrast, when the recording angle is greater than 90°, the coefficient increases with the recording angle. Obviously, the large angle is good for the observation of orthogonal reconstruction. For the given recording angle, the value of m/n could be calculated from Eq. (13), which determines the polarization state of reading wave.

In general, when the required recording angle is less than 90°, the signal and reference waves may enter the recording material from the same surface. In the above case, if the incident angles of signal and reference waves are equal, that is the symmetrical geometry is adopted, the recording angle inside the material can be calculated accurately. This geometry is suitable for the case, where the recording angle is acute.

In view of the previous analysis, we choose two obtuse angles, 120° and 150°, as the recording angles in the experiment. Since the refractive index of PQ/PMMA is about 1.51 at 532 nm, the optical waves should enter the material from different plane. To prevent the reading wave reflected by the material from entering the optical path of reconstructed wave, the asymmetrical geometry is adopted. It means that θ+ and θ– in Fig. 1 are not equal. When the reading wave illuminates the hologram, in addition to generating the reconstructed wave, the reading waves will also be reflected by the surface of the material. These two waves can be distinguished, because θ+ and θ– are not equal.

3 Experiments and Results

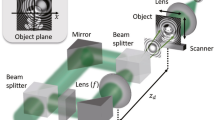
Based on the above analysis, we design the experiment shown in Fig. 4, where the angle between the signal and reference waves is 120° or 150° inside the recording material.

Fig. 4
figure 4

Schematic diagram of experiment. M mirror, HWP Half Wave Plate, QWP Quarter Wave Plate, P Polarizer, PBS Polarization Beam Splitter, BS Beam Splitter, SH Shutter, PM Power Meter, PQ/PMMA recording material

Full size image

The laser emits 532 nm linearly polarized wave. The polarization beam splitter 1 (PBS1) splits the laser into s and p polarized waves. Half wave plate 1 (HWP1) is to make the power of s-component and p-component equal. In the experiment, their powers are 52 mW. The s-polarized wave becomes the elliptically polarized wave after it passes through HWP3 and QWP1, which is used as the signal wave. The p-polarized wave becomes the elliptically polarized wave after it passes through HWP2 and QWP2, which is used as the reference wave and/or reading wave. When the reading wave illuminates the hologram, the reconstructed wave is divided into two beams by BS to check its polarization state. The transmitted part is used to detect the rotation direction, and the reflected part is used to detect the power of s- and p-components of reconstructed wave.

The recording stage lasts for 5 s and the reconstructing stage is 0.5 s. In the recording stage, SH1 and SH2 are opened, and SH3 is closed. After that, all the shutters are closed. During that time, HWP2 and QWP2 are rotated to the angle corresponding to the reading wave. During the reconstructing stage, SH2 is closed, and SH1 and SH3 are opened. The reading and reference waves are different, so HWP2 and QWP2 are placed on the electronic displacement table (KPRM1E/M, THORLABS Inc.). We have written a LabVIEW program that combines the rotation of HWP2 and QWP2 with the opening and closing of shutters to auto change the recording and reconstructing stages. In Table 1, we summarize the polarization states of signal, reference, and reading waves. Correspondingly, the azimuthal angle of fast axis of HWP2-3 and QWP1-2 are given, too. As shown in Table 1, the signal and reference waves are right- and left- handed elliptically polarized, respectively. Thus, if the orthogonal reconstruction is obtained, the reconstructed wave may be expressed as s-20.5ip+, which is left- handed elliptically polarized wave, and the ratio of s- to p- component corresponding to power is 1:2 in ideal case.

Table 1 Parameters in experiment
Full size table

Based on the experimental setup shown in Fig. 4, we get the experimental result shown in Fig. 5.

Fig. 5
figure 5

Experimental results of orthogonal reconstruction for a θ = 120° and b θ = 150°

Full size image

In Fig. 5a, when the recording angle is 120°, the powers of s- and p- components of reconstructed wave varying with the exposure time are given. In addition, the calculated ratio of s-component to p-component varying with the exposure time is given. In the experiment, the power of the ambient light is only 50 nW. Although the power of the reconstructed wave is only several microwatts, the experimental results are reliable. We could see when the exposure time is about 5.8 s, as point M indicates in Fig. 5a, the ratio is about 0.56. Theoretically, in ideal case, the power ratio of s- to p- component of reconstructed wave should be 0.5, which is not equal to that of point M. However, we still believe that the orthogonal reconstruction is reached at point M due to the anisotropic of recording material resulted from exposure. In the experiment, when the material is not placed, Ps:Pp of signal wave is 2:1. However, after the exposed material is placed, the above value becomes 1.8. Therefore, we think that the ratio of s- component to p- component of reconstructed wave should be 1/1.8 ≈ 0.56 when the orthogonal reconstruction is reached. Similarly, in Fig. 5b, we give the experimental results when the recording angle is 150°. After the exposed material is placed, the Ps:Pp of signal wave becomes 1.9. Thus, we think that the ratio of s- component to p-component of reconstructed wave should be 1/1.9 ≈ 0.53 when the orthogonal reconstruction is reached. We can see that when the exposure time is about 6.6 s, as indicated by point N, the power ratio is 0.53. By the powers of reconstructed and reading waves, it can be seen that the diffraction efficiency is about 0.2%. The short exposure time may account for the low diffraction efficiency. In addition, in this work, we focus on the polarization state of reconstructed wave rather than pursuing high diffraction efficiency. However, changing the technology of preparing material may improve the diffraction. For example, some new doping ion may be good for the improvement of diffraction efficiency [24].

Then, we check the rotation direction of reconstructed wave at points M and N. We convert rotation direction into the change of power. If the orthogonal reconstruction is reached, the rotation direction of reconstructed wave should be left- handed. In the experiment, the azimuthal angle of fast axis of QWP3 is vertical. Once the reconstructed wave passes through QWP3, it will become a linearly polarized wave vibrated in the first and third quadrants. At the beginning, the azimuthal angle of polarizer is horizontal. When the polarizer is rotated clockwise, the power would decrease to a minimum value and then increase. The experimental result is in good agreement with the prediction. Thus, we may claim that the orthogonal reconstruction is achieved. In addition, we find that the main difference between these two recording angles is the power of reconstructed wave corresponding to 150° is higher than that corresponding to 120°, which agrees with the curve shown in Fig. 3.

Now, we may explain why there is no report about orthogonal reconstruction before. Due to the limitation of Jones matrix, the angle between the signal and reference waves should be very small, which is not good for the observation of orthogonal reconstruction from Fig. 3. With the help of tensor polarization holography theory, we know that the coefficient of orthogonal reconstruction varies with the angle between the signal and reference waves. The obtuse angle is the key for orthogonal reconstruction, which may be the reason why it is difficult to achieve orthogonal reconstruction.

4 Discussion

Though we observe the orthogonal reconstruction when the signal, reference, and reading waves are elliptically polarized, we would like to give some conditions to observe the orthogonal reconstruction under different circumstances. When the signal and reference waves are orthogonal linearly polarized waves, it means that a = d = φ = ψ = δ = 0 and b = c = 1 in Eq. (8). Equation (8) becomes

$${\mathbf{G}}_{{\mathbf{F}}} \propto Bm{\mathbf{G}}_{ + } + Bn\cos \theta {\mathbf{G}}_{ + }^{^{\prime}} .$$
(14)

Obviously, to achieve orthogonal reconstruction, m = 0 and θ ≠ 90° are required, which indicates that reading wave should be p- polarized wave [25]. If the signal and reference waves are circularly polarized, we should take a = b = c = d = 1, φ = π/2, and δ =—π/2 in Eq. (8). Then, Eq. (8) may be rewritten as

$$\begin{gathered} {\mathbf{G}}_{{\mathbf{F}}} \propto {\mathbf{G}}_{ + } \left\{ {A\left( {1 - \cos \theta } \right)\left( {m - ine^{i\psi } \cos \theta } \right) + B\left[ {2\left( {m + ine^{i\psi } } \right) + \left( {m + ine^{i\psi } \cos \theta } \right)\left( {1 + \cos \theta } \right)} \right]} \right\} \hfill \\ \quad \quad + {\mathbf{G}}_{ + }^{^{\prime}} \left[ {A\left( {1 - \cos \theta } \right)\left( {m + ine^{i\psi } \cos \theta } \right) + B\left( {m + ine^{i\psi } \cos \theta } \right)\left( {1 - \cos \theta } \right)} \right], \hfill \\ \end{gathered}$$
(15)

Equation (15) also indicates that the obtuse angle is good for orthogonal reconstruction if the signal and reference waves are circularly polarized.

5 Conclusions

Based on the above analysis, we believe that the orthogonal reconstruction, like the faithful reconstruction and the null reconstruction, is a universal character in polarization holography.

In this work, we observe the orthogonal reconstruction in polarization holography, where the signal and reference waves are orthogonal elliptically polarized waves. The orthogonal reconstruction is not only a common phenomenon in polarization holography, but also very important to verify that the polarization holography may manipulate the polarization state of reconstructed wave freely. In the work, we find the key to observe the orthogonal reconstruction is the angle between the signal and reference waves should be obtuse.