Numerical analysis on the impact of optical feedback and nonlinear gain on the dynamics and intensity noise of semiconductor laser

Abstract

We demonstrate numerical analysis of the dynamics and noise of semiconductor laser (SL) with optical feedback (OFB) and nonlinear gain (NLG). The simulations are based on an improved time-delay rate equations model that takes into account the multiple round-trips of the lasing field in the external cavity. The temporal trajectory of the photon number, bifurcation diagrams, and relative intensity noise (RIN) is used to perform this analysis. The results show that when NLG included the Hopf bifurcation point moved towards the direction of increasing OFB strength. Period doubling, or sub-harmonics operation, is the route to chaos of SL depending on whether NLG is included or not. In the periodic oscillation (PO) and route to chaos regimes, including the NLG causes a significant frequency shift relative to the frequency in the case without NLG. Under strong OFB, the inclusion of NLG changes chaotic dynamics to continuous wave operation or PO depending on the OFB strength and characterized by RIN near to or higher than the RIN of the solitary laser. At high-frequency regime, the RIN is characterized by the compound cavity frequency or the external cavity frequency depending on the NLG whether included or not.

1 Introduction

Long-wavelength semiconductor laser (SLs), such as InGaAs/InP lasers, are of particular interest as radiation sources in optical communication systems [1]. The dynamics and noise of such lasers are strongly modified by optical feedback (OFB) from an external reflector. The variations in the dynamics of the SLs depend on various factors such as OFB strength, external cavity length, and injection current. While weak OFB levels result in line-width narrowing and improved frequency stability, moderate OFB levels might induce the laser to switch to a coherence collapsed state, which is characterized by spectral broadening and complex dynamics [1,2,3,4,5]. Strong OFB may cause dynamical complexity or stability depending on the strength of OFB and many other conditions [6].

The states or route to chaos is one of the interesting nonlinear phenomena associated with OFB; it may include dynamics with period doubling (PD), sub-harmonics (SH), or quasi-periodicity (QP) [7,8,9,10,11,12,13]. PD is observed in the short-external cavity [7, 9,10,11]; it follows a region of PO and is characterized by the PO frequency and its half harmonic. Kao et al. predicted that this frequency should correspond to the Hopf bifurcation (HB) point (the onset of PO) [9]. By increasing the external-cavity length, SH route to chaos was predicted as an intermediate state from PD to QP state, which is characterized by the HB frequency and one of its rational SH [9]. Ahmed et al. showed that the route to chaos is PD when the ratio of the relaxation frequency to the external cavity resonance frequency is less than unity [13]. Then the route to chaos becomes SH when the ratio is slightly higher than unity and less than 2.25. Abdulrhmann showed that laser operation changes from chaos or unstable operation to stable operation at higher values of injection current and NLG [14].

However, the dynamics and noise characteristics of the SLs are influenced by the NLG parameter, which is the origin of many complicated nonlinear phenomena such as mode competition phenomena, feedback noise, and gain suppression [15,16,17]. The upper limit of the modulation frequency of the laser is also controlled by the NLG coefficient [18,19,20,21].

Abdulrhmann et al. investigated numerically the effect of NLG on the quantum noise level in 1550-nm InGaAsP/InP SL without OFB [22]. The results show that by counting the NLG in the rate equations the RIN around the relaxation frequency is suppressed [22]. Recently, Al-Otaibi et al. used small-signal modeling to investigate the influence of NLG on the frequency characteristics of the RIN of solitary laser [23]. They showed that variation of damping rate and resonance frequency cause variation of the level of RIN with the form of NLG in the high-frequency regime (regime of resonance frequency) [23]. To the author’s knowledge, the influence of OFB (especially under a strong OFB regime) and NLG on the dynamics, operation states, route to chaos, and the associated RIN of SL have not yet been covered and are not fully understood because of its complexity.

In this article, we apply the time-delay rate equation model in [13, 14, 22] of OFB in SL to study the influence of OFB and NLG on laser dynamics, operation states, route to chaos and RIN. In such a model, OFB is treated as time delay of the SL radiation due to multiple round trips between the laser front facet and the external mirror. Intensive computer simulations were run to investigate the operation states, dynamics, and RIN of 1550-nm InGaAsP/InP SL with a short external cavity with and without NLG using a wide range of OFB strength. The bifurcation diagrams of the photon number versus feedback strength and with and without NLG are used to classify the route to chaos and laser operations.

In the next section, the time-delay rate equation model of OFB in SL is introduced. The procedures of numerical solution of rate equations are presented in Sect. 3. In Sect. 4, the bifurcation diagrams of the peak value of the photon number of SL over wide ranges of OFB strength and with and without NLG, and the corresponding variations of the RIN at low-frequency region are introduced. The simulation dynamics such as time variations and RIN under different operation states with and without NLG are also presented. In Sect. 5, the conclusion is presented.

2 Model of simulation

In the investigation of the influence of a wide range of OFB and NLG on the dynamics, operation states, and RIN of InGaAsP/InP laser emitting at 1550 nm the model in [13, 14, 22] was used. The time-delay rate equations of the carrier number N(t), photon number S(t), and optical phase θ(t) when counting the NLG and which describe the SL dynamics are formulated as

$$ \frac{{{\text{d}}N}}{{{\text{d}}t}} = - GS - N\left( {\frac{1}{{\tau_{{\text{s}}} }}} \right) + \frac{I}{e} + F_{N} (t), $$

(1)

$$ \frac{{{\text{d}}S}}{{{\text{d}}t}} = \left\{ {G - BS - G_{{{\text{th0}}}} + \frac{c}{{n_{r1} L}}\ln \left| T \right|} \right\}S \, + \frac{a\xi }{V}N + F_{{\text{S}}} (t), $$

(2)

$$ \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{\alpha a\xi }{{2V}}(N - \overline{N}) - \frac{c}{{2n_{{\text{r}}} L}}(\varphi - \overline{\varphi }) + F_{\theta } (t), $$

(3)

$$ G = \frac{a\xi }{V}(N - N_{{\text{g}}} ), $$

(4)

where G is the linear gain coefficient with a and N_g as material constants, τ_s is the electron lifetime due to spontaneous emission and ξ the confinement factor of the optical field into the active region of volume V. α is the line-width enhancement factor, I is the injection current and $\overline{N}$ is the corresponding time averaged carrier number. G_th0 is the threshold gain level and is determined by:

$$ G_{{{\text{th}}0}} = \frac{c}{{n_{{\text{r}}} }}\left\{ {k + \frac{1}{2L}\ln \frac{1}{{R_{{\text{f}}} R_{{\text{b}}} }}} \right\}, $$

(5)

where k is the loss coefficient of the laser and R_f and R_b are the reflectivity of the front and back facet, respectively.

Based on the density-matrix theory the gain nonlinearity has been presented in various models [24,25,26,27,28]. In this paper, the NLG is included in the rate equations in terms of coefficient B, which is given in the third-order perturbation theory of gain by [24, 25].

$$ B = \frac{{9\hbar \omega_{o} }}{{4\varepsilon_{o} n_{D}^{2} }}\left( {\frac{{\tau_{{{\text{in}}}} }}{\hbar }} \right)^{2} \left( {\frac{\xi }{V}} \right)^{2} a\left| {R_{{{\text{cv}}}} } \right|^{2} \left( {N - N_{{\text{s}}} } \right), $$

(6)

where R_cv is the dipole moment, τ_in is the intra-band relaxation time and N_s is an injection level characterizing the NLG. The influence of OFB on the threshold conditions is given by the complex coefficient T [6]:

$$ \begin{aligned} T & = 1 - \sum\limits_{m = 1} {\left( {K_{{{\text{ex}}}} } \right)^{m} \left( {\frac{{R_{{\text{f}}} }}{{1 - R_{{\text{f}}} }}} \right)}^{m - 1} \exp \left\{ { - jm\psi } \right\}\frac{S(t - m\tau )}{{S(t)}} \\ & = \left| T \right|\exp \left\{ { - j\phi } \right\}{\text{ and }}\phi = - \tan^{ - 1} \left\{ {{{{\text{Im}} \left[ T \right]} \mathord{\left/ {\vphantom {{{\text{Im}} \left[ T \right]} {{\text{Re}} \left[ T \right]}}} \right. \kern-\nulldelimiterspace} {{\text{Re}} \left[ T \right]}}} \right\} + \ell \pi , \\ \end{aligned} $$

(7)

where $\ell$ is an integer. The combined phase ψ_ex = ϕ_f + ϕ_f + ωτ where ψ_ex, ϕ_f, and ωτ are the phase retarded due to reflection by the external mirror, front facet, and round-trip in the external cavity, respectively. ω is the emission circular frequency and $\tau = {{2n_{{{\text{ex}}}} L_{{{\text{ex}}}} } \mathord{\left/ {\vphantom {{2n_{{{\text{ex}}}} L_{{{\text{ex}}}} } c}} \right. \kern-\nulldelimiterspace} c}$ is the round-trip time. m, R_ex, n_ex, and L_ex are an index for the round-trip in the external cavity, the reflectivity of the external mirror, refractive index, and the external cavity length, respectively.

The OFB strength is introduced by the coefficient K_ex, which is given by:

$$ K_{{{\text{ex}}}} = (1 - R_{{\text{f}}} )\sqrt {\eta \frac{{R_{ex} }}{{R_{{\text{f}}} }}} , $$

(8)

where $\ell$ is the coupling ratio of the injected light into the laser cavity.

The terms F_S(t), F_N(t), and F_θ(t) are Langevin noise sources with zero mean values, $\left\langle {F_{{\text{S}}} (t)} \right\rangle = \left\langle {F_{{\text{N}}} (t)} \right\rangle = \left\langle {F_{\theta } (t)} \right\rangle = 0$, and are assumed to have Gaussian probability distributions with their correlation functions defined as:

$$ \left\langle {F_{x} (t) \, F_{y} (t^{\prime})} \right\rangle = V_{xy} \delta (t - t^{\prime})\quad x,y = S,N{\text{ or }}\theta {,} $$

(9)

where $\delta (t - t^{\prime})$ is Dirac’s $\delta$ function and the quantities V_xy are the variances of the correlations and are determined by the mean values of S and N at each electron transition process of Eqs. (1)–(3) [22]. In the following section, we describe the method in which the variances and the noise sources are computed toward integrating the rate equations.

3 Procedures of numerical calculations

Equations (1)–(3) are solved numerically with the fourth-order Runge Kutta method. The simulation model is applied to InGaAsP/InP lasers emitting at the wavelength of 1550 nm. The threshold current of the solitary SL, I_th0 = 10.8 mA. The time step of integration is set as Δt = 5 ps, which is so short that the cutoff frequency of the Fourier transform of the laser signal is much higher than both the relaxation oscillation frequency, f_ro = 4.213 GHz, and the external cavity resonance frequency, f_ex = 2.5 GHz. The procedures of numerical calculations are clarified in Ref. [14]. The applied numerical values of InGaAsP/InP laser used in numerical simulation are given in Table 1 [14].

Table 1 Values of the parameters of 1550- nm InGaAsP/InP laser used in numerical simulation

A fundamental problem in treating the noise sources F_S(t), F_θ(t), and F_N(t) in the integration is that their mutual cross-correlations should be satisfied when generating the sources in each integration step. A systematic technique to overcome this difficulty is reported in [22]. The noise sources were generated at each sampling time t_i using three independent Gaussian random numbers g_S, g_θ, and g_N with zero means and variances of unity as,

$$ F_{{\text{S}}} (t_{i} ) = \sqrt {{{V_{{{\text{SS}}}} (t_{i} )} \mathord{\left/ {\vphantom {{V_{{{\text{SS}}}} (t_{i} )} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}} g_{{\text{S}}} , $$

(10)

$$ F_{\theta } (t_{i} ) = {1 \mathord{\left/ {\vphantom {1 {\left( {2\left[ {S(t_{i - 1} ) + 1} \right]} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\left[ {S(t_{i - 1} ) + 1} \right]} \right)}} \, \sqrt {{{V_{{{\text{SS}}}} (t_{i} )} \mathord{\left/ {\vphantom {{V_{{{\text{SS}}}} (t_{i} )} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}} g_{\theta } , $$

(11)

$$ F_{{\text{N}}} (t_{i} ) = \sqrt {{{V_{{{\text{NN}}}} (t_{i} ) + 2k(t_{i} )V_{{{\text{SN}}}} (t_{i} )} \mathord{\left/ {\vphantom {{V_{{{\text{NN}}}} (t_{i} ) + 2k(t_{i} )V_{{{\text{SN}}}} (t_{i} )} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}} g_{{\text{N}}} - k(t_{i} ) \, F_{S} (t_{i} ) - m(t_{i} ) \, F_{\theta } (t_{i} ) $$

(12)

with

$$ k(t_{i} ) = - {{V_{{{\text{SN}}}} (t_{i} )} \mathord{\left/ {\vphantom {{V_{{{\text{SN}}}} (t_{i} )} {V_{{{\text{SS}}}} (t_{i} )}}} \right. \kern-\nulldelimiterspace} {V_{{{\text{SS}}}} (t_{i} )}}, $$

(13)

$$ m(t_{i} ) = {{ - V_{{{\text{N}}\theta }} (t_{i} ) \, } \mathord{\left/ {\vphantom {{ - V_{{{\text{N}}\theta }} (t_{i} ) \, } { \, V_{\theta \theta } (t_{i} )}}} \right. \kern-\nulldelimiterspace} { \, V_{\theta \theta } (t_{i} )}} = 2k(t_{i} )\left[ {S(t_{i} ) + 1} \right]. $$

(14)

The variances V_xy(t_i) at time t_i were determined by the dc-values of S and N at the preceding time t_i−1 assuming quasi-steady states (${{{\text{d}}S} \mathord{\left/ {\vphantom {{{\text{d}}S} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} \approx {{{\text{d}}N} \mathord{\left/ {\vphantom {{{\text{d}}N} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} \approx 0$) during the interval $\Delta t = t_{i} - t_{i - 1}$ as,

$$ V_{{{\text{SS}}}} (t_{i} ) = {{2a\xi } \mathord{\left/ {\vphantom {{2a\xi } V}} \right. \kern-\nulldelimiterspace} V}\left( {S(t_{i - 1} ) + 1} \right)N(t_{i - 1} ), $$

(15)

$$ V_{{{\text{NN}}}} (t_{i} ) = \left( {{{2N(t_{i - 1} )} \mathord{\left/ {\vphantom {{2N(t_{i - 1} )} {\tau_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {\tau_{{\text{s}}} }}} \right) \, \left( {1 + {{a\xi \tau_{{\text{s}}} } \mathord{\left/ {\vphantom {{a\xi \tau_{{\text{s}}} } V}} \right. \kern-\nulldelimiterspace} V} \, S(t_{i - 1} )} \right), $$

(16)

$$ V_{{{\text{SN}}}} (t_{i} ) = G_{{{\text{th}}}} S(t_{i - 1} ) - 2{{a\xi \tau_{{\text{s}}} } \mathord{\left/ {\vphantom {{a\xi \tau_{{\text{s}}} } V}} \right. \kern-\nulldelimiterspace} V} \, N(t_{i - 1} )\left( {S(t_{i - 1} ) + 1} \right) $$

(17)

with the relations

$$ V_{\theta \theta } (t_{i} ) = {{V_{{{\text{SS}}}} (t_{i} ) \, } \mathord{\left/ {\vphantom {{V_{{{\text{SS}}}} (t_{i} ) \, } { \, \left[ {4\left( {S(t_{i - 1} ) + 1} \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} { \, \left[ {4\left( {S(t_{i - 1} ) + 1} \right)^{2} } \right]}}, $$

(18)

$$ V_{{{\text{N}}\theta }} (t_{i} ) = {{V_{{{\text{NS}}}} (t_{i} )} \mathord{\left/ {\vphantom {{V_{{{\text{NS}}}} (t_{i} )} { \, \left[ {2\left( {S(t_{i - 1} ) + 1} \right)} \right]}}} \right. \kern-\nulldelimiterspace} { \, \left[ {2\left( {S(t_{i - 1} ) + 1} \right)} \right]}}. $$

(19)

The Gaussian random numbers g_S, g_N, and g_θ were generated at each time step by applying the Box-Mueller approximation to a set of uniformly distributed random numbers generated by the computer [29].

Analyses of the intensity fluctuations in the frequency domain are given in terms of the RIN, which was calculated as the power density function of the fluctuations in the output photon number δS(t) = S(t) − $\overline{S}$ as

$$ {\text{RIN}} = \frac{1}{{\overline{S}^{2} }}\left\{ {\frac{1}{T}\int\limits_{0}^{T} {\left[ {\int\limits_{0}^{\infty } {\delta S(t)\delta S(t + \tau )e^{j\omega \tau } {\text{d}}\tau } } \right]{\text{d}}t} } \right\} = \frac{1}{{\overline{S}^{2} }}\left\{ {\frac{1}{T}\left| {\int\limits_{0}^{T} {\delta S(\tau )e^{ - j\omega \tau } {\text{d}}\tau } } \right|^{2} } \right\}{,} $$

(20)

where $\overline{S}$ is the dc-value of S(t). The value of $\overline{S}$ is timely averaged values of the photon number which are also examined by numerical calculations. The calculations of RIN were carried out when the steady-state operation is attained (t ≈ 4–6 µs).

4 Results and discussions

We simulate the variations of laser dynamics and noise over a wide range of the OFB strength (in terms of K_ex), and with and without NLG.

4.1 Influence of OFB and NLG on the dynamics and operation states of InGaAsP/InP SL

Investigation of the effects of OFB and NLG on laser dynamics and operation states is done by simulating the bifurcation diagram of the photon numbers S(t) in terms of the OFB strength K_ex. To characterize operation states of SL the OFB strength K_ex is varied over a wide range (from very weak to very strong OFB). The bifurcation diagrams with ignoring noise sources in the rate Eqs. (1–3), and with and without NLG are plotted in Fig. 1, respectively, when the injection current ratio is I/I_th0 = 2.0. In this figure, we are interested in exploring an overview of the impact of OFB strength and NLG on the operation states of SL.

Fig. 1

Bifurcation diagrams of a SL with OFB strength K_ex at I/I_th0 = 2.0, without noise sources, red empty circle and black solid circle without and with NLG, respectively

Under very weak OFB, the solution of the rate equations is still stationary and the laser operates in continuous wave (CW) as shown in Fig. 1. By increasing OFB strength, K_ex, this stationary solution bifurcates first into a stable limiting cycle characterizing PO (un-damped relaxation oscillation with and without NLG). The starting point of the bifurcation is called a HB point, which is indicated in Fig. 1 by the arrow, is moved to higher values of the OFB strength K_ex by including NLG in the rate equations; from 0.004 to 0.008.

With further increase in OFB strength, when NLG is not included, shows that PO is followed by tours (multiple bifurcation points), which is called a SH route to chaos [9] and followed by a chaotic state, and then the laser is attracted again to CW and chaos operation depending on the strength of the OFB. When NLG is included, the SH tours changed to the PD route to chaos in which PO bifurcates first into two branches as shown in Fig. 1, where the trajectory of S(t) has two peaks of different heights in every two successive intervals. That is, the inclusion of NLG into the rate equations changes the route to chaos of the laser from the SH type to the PD type, which contributes to improving the stability of SL.

With the increase in strength of OFB, K_ex, the PO is multiplied more than twice and the laser is attracted to transition to chaos. The width of the chaotic region changed from (0.022–0.459) to (0.024–0.339) by including the NLG in the rate equations as shown in Fig. 1, which means that including the NLG in the rate equations narrowed the chaotic region and led to more stability in the laser.

By strengthening OFB beyond the chaotic region under strong OFB and when NLG is not included, we find that the laser operates in the CW region (0.46–1.4 and 1.42–2.198) then changed to the chaos region (2.198–2.2 and 2.2-end). By including the NLG and under strong OFB the laser oscillates in CW and pulsing region (0.339-end) depending on the OFB strength. Under strong OFB and by counting the NLG parameter in the rate equations the laser stability is improved and moves toward stable operations.

The starting point of the bifurcation is called a HB point and is characterized by frequency f_po(H), which is not necessarily equal to the relaxation oscillation frequency f_ro. Figure 2 plots the variation of the periodic oscillation frequency ratio f_po/f_ro with K_ex from HB point till route to chaos. The figure reveals that the frequency f_po decreases below f_po(H) with the increase in OFB strength in both cases with and without NLG. By including the NLG the PO region becomes narrower as shown in Fig. 1 and the values of f_po/f_ro becomes smaller as shown in Fig. 2.

Fig. 2

Variation of the periodic oscillation frequency ratio f_po/f_ro with K_ex from HB point till route to chaos

From Figs. 1 and 2, we found that the impacts of the wide range of OFB strength and NLG parameters on the operation states of the SL are opposite, which confirms Masoller’s results under weak OFB [20]. For example, we find that the width of the pulsing region under weak OFB and chaotic region under moderate OFB becomes narrower by including the NLG parameter in the rate equation, which leads to a more stable laser. Moreover, the route to chaos changed to a more stable route to chaos from SH to PD route to chaos. Under strong OFB the operation states become more stable by including NLG parameter the chaotic region changed to CW and pulsing operation. That is means that further increase of OFB strength causes the laser to lose stability. Contrarily including the NLG parameter in the rate equations reverses the route to chaos to be simple and the laser operation states recover their stability, especially under strong OFB.

4.2 Dynamis of SL in terms of time variation, and RIN of S(t) for various states

In this section, we examine the time variations and RIN of S(t) of SL with and without OFB, and with and without the NLG parameter. The examination is taken over a wide range of OFB strength from weak OFB to strong OFB and when injection current I/I_th0 = 2.0.

The simulated time variations of S(t)/$\overline{S}$ and corresponding RIN, with and without NLG and without OFB, K_ex = 0.0, are plotted in Fig. 3a, b, respectively. The fluctuations of S(t)/$\overline{S}$ are suppressed by the inclusion of the NLG as shown in Fig. 3a. The suppression of the fluctuations of S(t)/$\overline{S}$ is seen in Fig. 3b as suppression of RIN around the relaxation frequency. However, the gain saturation has no effect on the low-frequency components of RIN.

Fig. 3

a Time, and b RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 0.0 (solitary laser), with and without NLG

Under weak OFB, and at HB points when K_ex = 0.004 and 0.008, the simulated time variation of S(t)/$\overline{S}$, and corresponding RIN with and without NLG are shown in Fig. 4. The fluctuations of the S(t)/$\overline{S}$ are strongly suppressed by the inclusion of the NLG and OFB as shown in Fig. 4a, c. The suppression of the fluctuations of S(t) is seen in Fig. 4b, d as suppression of RIN around the periodic oscillation frequency f_po(H) at the HB point. We noticed that the laser changes its oscillation frequency from relaxation oscillation frequency f_ro in the case of solitary laser to periodic oscillation frequency f_po(H) at HB point and this is due to the OFB effect, which is strong enough to modulate the relaxation oscillation frequency f_ro of the laser to PO frequency f_po(H). Moreover, Fig. 4b, d, show that the low-frequency RIN suppressed more than half an order of magnitude and close to the solitary laser noise by including the NLG.

Fig. 4

a, c Time without noise sources, and b, d the corresponding RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 0.004 and 0.008 (HB), with and without NLG, respectively

By increasing the strength of the OFB and under a weak OFB regime when K_ex = 0.01, the simulated time variation of the photon number S(t)/$\overline{S}$(without noise sources) and corresponding RIN are shown in Fig. 5. The fluctuations of S(t)/$\overline{S}$ are strongly suppressed and phase-shifted on the inclusion of the NLG and OFB as shown in Fig. 5a. The suppression of the fluctuations of S(t) is seen in Fig. 5b as suppression of RIN around the periodic oscillation frequency f_po. The phase shift appeared in Fig. 5a by including NLG translated to a frequency shift in the RIN spectra in Fig. 5b and suppressed the low-frequency RIN by more than half an order of magnitude and close to the solitary laser noise. These results are in good agreement with the experimental and theoretical results reported in Refs. [30,31,32]. From the above results, under weak OFB and when the laser operated in the PO region we conclude that although the NLG works to reduce the laser instability and noise (i.e., improve the noise characteristics) as shown in Fig. 5, it causes significant shifts in the lasing wavelength and degrades the efficiency of the SL in applications [33].

Fig. 5

a Time without noise sources, and b the corresponding RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 0.01 (PO), with and without NLG, respectively

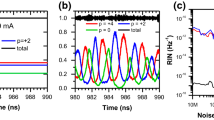
Under a weak to moderate OFB regime and by increasing the OFB strength to K_ex = 0.02, which represent the regions of the route to chaos, the laser operation becomes more complicated and the system nonlinearity increases the irregularities in S(t) attracting the laser oscillation into a kind of periodic variation operation such as SH and PD oscillations. These two types of the route to chaos appear in Fig. 6a by ignoring the noise sources in the rate equations. When NLG is not included, the SH route to chaos is indicated by the four different peaks, which change to two peaks by including NLG in the rate equations, these features represent the PD route to chaos as defined in Fig. 1. The suppression of the fluctuations of S(t) is confirmed in Fig. 6b, as suppression of RIN around the PO frequency f_po, and its harmonics. Still, the phase shift appeared in Fig. 6a by including NLG, which is translated to a frequency shift in the RIN spectra in Fig. 6b and suppressed the low-frequency RIN more than half an order of magnitude and close to the solitary laser level. In the periodic oscillation (PO) and route to chaos regimes, including the NLG causes a significant frequency shift induced phase shift relative to the frequency in the case without NLG. These obtained results, to the best of the authors' knowledge, are new contributions to the dependence of the lasing frequency shift on the OFB and NLG parameters of the SL.

Fig. 6

a Time without noise sources, and b the corresponding RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 0.02 (route to chaos), with and without NLG, respectively

Under higher OFB with K_ex = 0.1 (moderate OFB), which represented by chaotic operation. The time variations and RIN of the S(t) are plotted in Fig. 7. As found in Fig. 7a, chaos is indicated by random variations of S(t). Figure 7b, shows the RIN spectra characterizing the chaotic dynamics. Spectral peaks can be seen at frequencies higher and nearly equal to the relaxation frequency f_ro, with suppression in the power spectrum around it by including the NLG parameter. The RIN is enhanced here by increasing OFB strength to be higher than that represented by quantum noise level five orders of magnitude.

Fig. 7

a Time without noise sources, and b the corresponding RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 0.1 (chaotic operation (chaos) moderate feedback), with and without NLG, respectively

Under strong OFB and when K_ex = 3.0, the time variations and RIN of S(t) are plotted in Fig. 8. As found in Fig. 8a, the laser fluctuations changes from random variations of S(t) (chaotic state) to approximately constant variation with time (CW state) by counting the NLG in the rate equations. The corresponding frequency spectra of RIN are presented in Fig. 8b. The RIN spectra show that the low-frequency RIN of the chaos state (without NLG) is enhanced by increasing OFB strength to be higher than that represented RIN of the CW state and quantum noise level six orders of magnitude. In the chaotic state (without NLG) spectral peaks can be seen at frequencies nearly equal to the external cavity frequency f_ex, and its harmonics. By including NLG and in the CW state spectral peaks can be seen at frequencies nearly equal to the average of the external cavity frequency f_ex, and relaxation oscillation frequency f_ro, which we will call here the compound cavity frequency f_c = (f_ex + f_ro)/2.0, and its harmonics. Adding the NLG parameter to the rate equations and operating the SL under strong OFB leads to a change in operation state from an unstable state (chaotic state) to more stability (CW state) and oscillation frequency from eternal cavity frequency f_ex to compound cavity frequency f_c.

Fig. 8

a Time without noise sources, and b the corresponding RIN variations of photon number S(t) when I/I_th0 = 2.0, OFB strength K_ex = 2.0 (strong feedback), with and without NLG, respectively

4.3 Influence of OFB and NLG on the low-frequency RIN of InGaAsP/InP SL

The variation of the RIN averaged over low frequencies, when f < 10 MHz, with the OFB strength with and without NLG is plotted in Fig. 9. As shown in the figure, the average RIN under weak feedback is suppressed to the quantum noise level, which corresponds to the solitary laser in both cases with and without NLG. In the region from HB point to the route to chaos, the RIN is suppressed approximately to the solitary laser noise level (more than half order of magnitude) as shown in Figs. 4, 5 and 6. The disturbance characterizing the chaotic state under moderate OFB raises the RIN to much higher levels above the quantum level (more than 5 orders of magnitude). As shown in Fig. 9, the average RIN under strong OFB and by including NLG is suppressed approximately to the quantum noise level. Under strong OFB and when NLG has not included the instabilities characterizing the chaotic operation increases the level of the RIN to 6 orders of magnitude of the quantum level approximately. By accounting for the NLG in the rate equations the chaotic operation changed to the CW state as shown in Fig. 1 and the RIN is decreased approximately near to the quantum level.

Fig. 9

The RIN levels averaged over f < 10 MHz when I/I_th0 = 2.0, red circle (straight line) and black solid circle (dashed line) without and with NLG, respectively

5 Conclusions

We numerically investigate the influence of OFB and NLG on the dynamics, operation states, route to chaos, and RIN of SLs. The simulations were applied to 1550-nm InGaAsP/InP laser over a wide range of OFB with and without the inclusion of NLG in the rate equations. The dynamics, route to chaos, and operation states of SL are classified by the bifurcation diagrams of the photon number. The time variations of the fluctuations of the photon number and RIN spectrum as functions of NLG, through several operation states of SLs, are calculated. The simulation results showed that the inclusion of the NLG in the time delay rate equations of SL causes significant changes in the operation states, route to chaos, and RIN of the SL. We found that the values of the feedback strength at which the transitions from CW to PO, HB point, or coherence collapsed state (or chaos) occur increases with the inclusion of the NLG. Including NLG in the time delay rate equations was found to change the route to chaos of the short external cavity InGaAsP/InP SL from the SH type to the PD type. In the periodic oscillation (PO) and route to chaos regimes, including the NLG causes a significant frequency shift induced phase shift relative to the frequency in the case without NLG. These obtained results, to the best knowledge of the authors, are new contributions to the dependence of the lasing frequency shift on the OFB and NLG parameters of the laser. The RIN is suppressed near to quantum noise level when the laser is operated in CW or PO region, which occurs when the NLG is counted in the time delay rate equations. Adding the NLG parameter to the rate equations and operating SL under a strong OFB regime leads to improvements in the operation state of SL from an unstable state (chaotic state) to a more stable state (CW). Moreover, a frequency locked has been noted at external cavity frequency f_ex or compound cavity frequency f_c in the regime of strong OFB depending on whether NLG is included or not. We believe that the stability of SLs can be improved by taking into account the influences of OFB and NLG, which helps to design a high-performance SL.