1 Introduction

Measuring frequency ratios between different types of optical clocks are important for metrology and fundamental physics research, e.g. the redefinition of the unit second [1, 2] and the demonstration of the time constancy of the fine structure constant [3,4,5]. Currently, optical clocks are commonly at the level of \(10^{-18}\) for both systematic uncertainty and frequency instability [6,7,8,9], and the cutting edge is still better [10, 11]. They are hundred times better than the Caesium clocks, i.e. the definition of SI-second. It is not possible to measure the absolute frequencies of optical clocks to their limits under the current definition. However, the frequency ratios between different clock transitions are dimensionless and can be measured with higher precision. Moreover, measuring frequency ratios among different clocks at independent laboratories can be used to verify the agreement of optical frequency standards [2].

With optical frequency comb (OFC) linking RF and optical frequencies, methods for measuring optical frequency ratios (OFRs) are developed. For example, one method is to stabilize the repetition rate of the OFC by phase locking the beating signal of one stable laser and the comb to an RF reference, thus coherently linking two optical frequencies. Another is the transfer oscillator scheme (TOS) [12, 13] by generating a “virtual beat signal” of two optical fields through RF signal processing. Based on these methods, ratios of different optical clocks were measured to the level of \(10^{-16}\)–\(10^{-18}\) uncertainty [14,15,16,17,18,19]. There were also works on synthesizing lasers with OFC reaching the precision to \(10^{-21}\) level [20, 21], which were also used for optical frequency ratio measurement.

In this work, we built an RF processing system for high-precision OFR measurement. It was based on a self-reference direct-measuring scheme. The scheme was developed from the TOS and Yao’s method [20]. The mathematical construction of the RF processing scheme was described in detail to help understanding the scheme. To demonstrate the RF processing system, an OFR measuring experiment was carried out to measure the ratio between the second harmonic and fundamental frequencies of a 1560-nm ultrastable laser. In one day’s measurement, an offset of \(2+1.2\times 10^{-22}\pm 1.4\times 10^{-21}\), and fractional frequency instabilities of \(5\times 10^{-19}\) at the averaging time of 1 s and less than \(2\times 10^{-21}\) at 1000– 10,000 s were obtained. This result suggested that the scheme and the RF processing system were suitable for precision OFR measurement to the level \(10^{-21}\). This system was built for the comparison of \(\mathrm {^{40}Ca^{+}}\), \(\mathrm {^{27}Al^{+}}\) and \(\mathrm {^{171}Yb}\) optical clocks in the Innovation Academy for Precision Measurement Science and Technology, CAS [9, 22,23,24].

2 Mathematical construction of the OFR measuring scheme

Fig. 1
figure 1

The frequency relation between CW lasers and OFC when they beat with each other. The beat notes detected by photo detectors (PD) are the frequency differences between the CW laser and corresponding nearby comb modes

Full size image

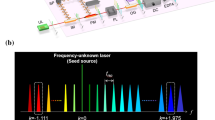
The mathematical construction of the OFR measuring scheme is described as follows. As illustrated in Fig. 1, the spectrum of an OFC can be written as

$$\begin{aligned} \nu _{\mathrm {OFC}} = \sum _n n f_{\mathrm {r}} + f_{\mathrm {CEO}}, \end{aligned}$$
(1)

where \(f_\mathrm {r}\) is the repetition rate, \(f_{\mathrm {CEO}}\) is the carrier envelope offset frequency, and n is the longitude mode number of the OFC, respectively. When a continuous wave (CW) laser with frequency \(\nu\) beats with the m-th mode of the OFC, their frequency relation can be written as

$$\begin{aligned} \nu =mf_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b}}, \end{aligned}$$
(2)

where \(f_{\mathrm {b}}\) is the beating frequency between the CW laser and the m-th mode of the OFC. When \(f_{\mathrm {r}}\) and \(f_{\mathrm {CEO}}\) are phase locked to RF references, the integer m can be calculated using a high-precision wavemeter with accuracy of 10’s MHz level to measure \(\nu\). According to Eq. (2), when two lasers \(\nu _1\) and \(\nu _2\) beat with an OFC simultaneously, their frequency ratio R can be written as

$$\begin{aligned} R=\frac{\nu _2}{\nu _1}=\frac{m_2f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b2}}}{m_1f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b1}}}=\frac{m_2+x}{m_1}, \end{aligned}$$
(3)

where

$$\begin{aligned} x=\frac{m_1\nu _2-m_2\nu _1}{\nu _1}=\frac{m_1\left( f_{\mathrm {CEO}}+f_{\mathrm {b2}}\right) -m_2\left( f_{\mathrm {CEO}}+f_{\mathrm {b1}}\right) }{m_1f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b1}}}\ . \end{aligned}$$
(4)

The ratio R is the function of two mode numbers \(m_1\), \(m_2\) and a decimal part x. x is the function of \(m_1\), \(m_2\), and the RF signals \(f_{\mathrm {r}}\), \(f_{\mathrm {CEO}}\), \(f_{\mathrm {b1}}\), and \(f_{\mathrm {b2}}\). Because \(m_1\) and \(m_2\) are known integers, the measurement of R is then turned to the obtaining of x with high precision. The repetition rates of OFCs used at visible and near infrared region are usually around 200 MHz. Therefore, \(m_1\) is at the order of around \(10^6\). The requirement on the accuracy of x is \(10^6 (m_1)\) times lower than that of R, i.e., a \(10^{-21}\) level precision of R measurement is changed to the RF processing and measuring procedures at the level of about \(10^{-15}\).

The value of x can be derived from measuring the frequencies of the RF signals in Eq. (4) directly. This is the method commonly used in TOS. They divided the numerator and denominator with \(m_1\), and then measured the virtual beat between the two lasers in the numerator and the absolute frequency of \(\nu _1\) in the denominator. In this work, we obtain the value of x directly, by using one single frequency measurement of an RF signal. The idea is to generate RF signals proportional to the numerator and denominator of Eq. (4), and measure their ratio using an RF instrument. To realize this purpose, the numerator and denominator of Eq. (4) are multiplied by a small factor k simultaneously, and noted as \(f_{\mathrm {diff}}\) and \(f_{\mathrm {ref}}\), as shown in Eq. (5),

$$\begin{aligned} \begin{aligned}&f_{\mathrm {diff}}=k\times m_1\left( f_{\mathrm {CEO}}+f_{\mathrm {b2}}\right) -k\times m_2\left( f_{\mathrm {CEO}}+f_{\mathrm {b1}}\right) ,\\&f_{\mathrm {ref}}=k\times \nu _1=k\times \left( m_1f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b1}}\right) . \end{aligned} \end{aligned}$$
(5)

Frequency counters can be used to measure the ratio between \(f_{\mathrm {diff}}\) and \(f_{\mathrm {ref}}\). It is realized as follows, a proper k is chosen to let \(f_{\mathrm {ref}}\) close to 10 MHz, then this \(f_{\mathrm {ref}}\) signal is used as the reference frequency of the frequency counter. The counter will take \(f_{\mathrm {ref}}\) as a precise 10 MHz and perform frequency measurement in the unit of 10 MHz/\(f_{\mathrm {ref}}\). \(f_{\mathrm {diff}}\) is scaled with the same factor and sent to the counter’s input. The counter will return a frequency value \(f_{\mathrm {dm}}\), which is the value of \(f_{\mathrm {diff}}\) in the unit of 10 MHz/\(f_{\mathrm {ref}}\), i.e., \(f_{\mathrm {dm}}=f_{\mathrm {diff}}/f_{\mathrm {ref}}\times 10\text { MHz}\). Therefore, \(x=f_{\mathrm {dm}}/(10^{7}\text { Hz})\). There is no external reference involved in this procedure, and therefore, no reference error is introduced in the measured result. The precision depends only on the RF processing procedure and the frequency counter.

Dividing \(\nu _1\) from a level of 2–\(4\times 10^{14}\) Hz to around 10 MHz, k is about 2.5–\(5\times 10^{-8}\) and \(k\cdot m_i\) is at the level of 0.01, which is a proper ratio for the processing of \((f_{\mathrm {CEO}}+f_{\mathrm {bi}})\) to generate \(f_{\mathrm {diff}}\). For the generation of \(f_{\mathrm {ref}}\), because \((f_{\mathrm {CEO}}+f_{\mathrm {b1}})\) is at the ppm level of \(m_1f_{\mathrm {r}}\), when \(f_{\mathrm {ref}}\approx 10\) MHz, \(k\times ( f_{\mathrm {CEO}}+f_{\mathrm {b1}})\) is at the level of 10 Hz, which is very difficult for RF processing. Therefore, \(f_{\mathrm {ref}}\) is reformed according to the method used in [20],

$$\begin{aligned} f_{\mathrm {ref}}= k\times m_1\left( f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b1}}\right) -k\times (m_1-1)\left( f_{\mathrm {CEO}}+f_{\mathrm {b1}}\right) . \end{aligned}$$
(6)

In this form, the frequency values of \(k\times m_1(f_{\mathrm {r}} + f_{\mathrm {CEO}}+f_{\mathrm {b1}})\) and \(k\times (m_1-1)( f_{\mathrm {CEO}}+f_{\mathrm {b1}})\) are comparable, and the processing of \(f_{\mathrm {ref}}\) is possible.

Fig. 2
figure 2

The schematic diagram of RF processing and OFR measuring procedure. The \(\oplus\), \(\ominus\), and \(\times k\times m_i\) denote the addition, subtraction and scaling of the corresponding RF signals’ frequencies. Filters and amplifiers are not shown in the diagram

Full size image

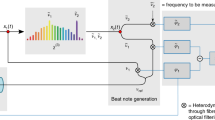
According to the above mathematical construction, the scheme for the RF signal processing and the OFR measuring procedure is shown in Fig. 2. Here \((f_{\mathrm {r}}+f_{\mathrm {b1}})\) can be directly obtained by the beat note between \(\nu _1\) and the \((m-1)\)-th comb tooth, as indicated in Fig. 1. The addition and subtraction of radio frequencies are realized using double balanced mixers (DBM) together with proper band-pass filters to pick up the target signals. Direct digital synthesizers (DDS) are used to execute the frequency scaling.

Comparing with previous relative works, there are several differences in this scheme. First, one single-channel frequency counter is introduced to measuring the x directly. Therefore, higher precision frequency counter can be chosen to do the measurement, e.g., the precision of single-channel frequency counter (e.g., Symmetricon 3120A) can reach the level of 17 digits, while multi-channel counter (e.g. K+K FXE) is at the level of 15 digits, and the requirement on the synchronization between channels does not exist either. Second, the frequencies of the RF signals are scaled with the factors proportional to \(m_i\)s, which meet the designed function of DDSs, whose output frequencies are scaled with factors of FTW\(/2^{N}\) (where FTW is the setting frequency tuning word and N is the maximum digits of the FTW, which depends on the DDS selected). Third, when adapting the scheme for optical frequency synthesizing, this scheme does not suggest additional RF synthesizer for setting offset frequency, as used in [20].

3 Experimental demonstration of the RF processing system

According to the scheme shown in Fig. 2, an RF processing system for OFR measurement was built. To demonstrate the precision of the system, an experiment on measuring the ratio between the second-harmonic and fundamental frequencies of a 1560-nm ultrastable laser was carried out. The ratio should be exactly 2 in theory. An erbium-fiber based OFC with repetition rate at 200 MHz, which was supplied by National Time Service Center (NTSC), CAS, was used in this test.

Fig. 3
figure 3

The optical setup of the test experiment. EDFA: erbium doped fiber amplifier. HNLF: highly nonlinear fiber

Full size image

The optical setup for the test is shown in Fig. 3. The output of the mode-locked femtosecond oscillator is split into several branches and amplified for different applications. One is used for generating and detecting the CEO frequency via an f-2f interferometer. The second branch is used to beat with the 1560-nm ultrastable laser \((\nu _1)\). The branch is combined with the laser using a beam splitter and then passes through a Periodically-Poled Lithium Niobate (PPLN) crystal. In the crystal, the second harmonic of the \(\nu _1\) and the OFC, together with their sum frequency, noted as \(\nu _2\), \(\nu '_{\mathrm {OFC}}\), and \(\nu _{1+\mathrm {OFC}}\) respectively, are generated. The output spectra of the lasers are as follows,

$$\begin{aligned} \begin{aligned} \nu _2&=2\nu _1\,,\\ \nu _{\mathrm {OFC}}'&=\sum _n n f_{\text {r}} + 2f_{\mathrm {CEO}},\\ \nu _{\mathrm {1+OFC}}&=\nu _1+\nu _{\mathrm {OFC}}=\sum _n n f_{\text {r}} + 2f_{\mathrm {CEO}}+f_{\mathrm {b1}},\\ ... \end{aligned} \end{aligned}$$
(7)

Equation (7) showed that the output of the photo detector (PD) in the second branch at visible light range includes the beat notes of the fundamental laser with OFC \((f_{\mathrm {b1}}=\nu _{1+\mathrm {OFC}}-\nu _{\mathrm {OFC}}'=\nu _1-\nu _{\mathrm {OFC}})\), and that of the second harmonic laser with the frequency doubled OFC \((f_{\mathrm {b2}}=\nu _2-\nu _{\mathrm {OFC}}')\). In this optical setup, the optical paths for the two beating signals are in common mode, and there is no optical path noise introduced. This setup demonstrates the limit of our RF processing system.

In the experiment, the signal-to-noise ratio (SNR) of the beating signals \(f_{\mathrm {CEO}}\), \(f_{\mathrm {b1}}\) and \((f_{\mathrm {r}}+f_{\mathrm {b1}})\) were about 40 dB at a resolution bandwidth (RBW) of 300 kHz, and of \(f_{\mathrm {b2}}\) was about 30 dB. The output of the PD in the second branch was split and filtered with different bandpass filters to pickup \(f_{\mathrm {b1}}\), \((f_{\mathrm {r}}+f_{\mathrm {b1}})\) and \(f_{\mathrm {b2}}\), and then added with \(f_{\mathrm {CEO}}\) (frequency-doubled \(f_{\mathrm {CEO}}\) for \(f_{\mathrm {b2}}\)) by using DBMs. Because the SNR of the mixers’ output signals were not high enough, which were at the level of about 30 dB, the same as the worst SNR of the input signals, and the amplitudes were too small, it was difficult for DDSs to track the signals directly. Therefore, tracking oscillators (TOs) were introduced to pick up, amplify, and normalize the amplitudes of the RF signals.

Fig. 4
figure 4

Results on testing the TOs. a is the spectrum of the beat signal pre-processed by a 20-MHz bandpass filter and an RF amplifier. b is the same signal filtered by a TO. c is the result of two TOs tracking one beat signal. The upper figure shows the original output frequencies and the lower shows their difference. d is the Allan deviation of the frequency difference in (c)

Full size image

The TOs were built by analog phase locking of voltage-controlled oscillators (VCO, Mini-Circuits JTOS series) to the input signals. The effects of the TOs were presented in Fig. 4. Figure 4a, b showed the spectra of the mixed-up signal \((f_{\mathrm {CEO}}+f_{\mathrm {b1}})\) before and after TO filtered. It showed that the amplitude of the RF signal was normalized to about 1 dBm, the SNR in the bandwidth of 1 MHz was maintained at the same level, while the noise outside the bandwidth of 15 MHz was suppressed to \(-70\) dBm. Figure 4c showed the frequency difference between two TOs tracking the same signal at about 303 MHz. The measurement was carried out using a K+K FXE multi-channel frequency counter (\(\Pi\)-type), which measured the outputs of the two TOs simultaneously with reporting interval of 1 s. In one day’s measurement, the frequency difference between the two TOs was 60 nHz ± 2.1 \(\upmu\)Hz, which was \(2\times 10^{-16} \pm 7\times 10^{-15}\) related to the carrier frequency. Figure 4d was the Allan deviation of the frequency difference shown in (c). This result suggested that precision of the TO was enough for OFR measurement at the level \(10^{-21}\).

The DDSs used to scale the frequencies of the RF signals were Analog Devices AD9956, which had 48 bits frequency tuning word (FTW). With the DDSs, the frequency scaling coefficients could be written as \(c\times m/2^{48}=k\times m\), where \(c\times m\) was the FTW written to the DDS. c was set as integers, which introduced no systematic offset to the system theoretically. \(m/2^{48}\) was about \(3.5\times 10^{-9}\) when \(m=10^6\). Therefore, when c was changed by step of 1, the frequency of the generated \(f_{\mathrm {ref}}\) changed in step of about 1 Hz, which was precise enough for using as the reference of the frequency counter. The precision of the DDS was tested by comparing the output of the DDS, whose FTW was set to \(2^{46}\), i.e., the output frequency was 1/4 of the input, with a divide-by-4 static divider Analog Devices HMC433 using the FXE counter. The input was the output of the TO tracking the signal in Fig. 4. The result was shown in Fig. 5. Figure 5a showed that the frequency difference between the two processing was 4.2 nHz ± 0.59 \(\mu\)Hz, which was \(1.6\times 10^{-17} \pm 2\times 10^{-15}\) related to the carrier frequency. The result suggested that using DDS to scale the frequency of the RF signal was also precise enough for the OFR measurement at the level \(10^{-21}\).

Fig. 5
figure 5

Results for testing the precision of DDS. a The frequency difference between the output of the DDS and the static frequency divider. b Allan deviation of the frequency differences of (a)

Full size image

In the experiment, \(f_{\mathrm {CEO}}\) and \(f_{\mathrm {r}}\) were phase locked to 244 MHz and 200.003979 MHz related to a H-maser, respectively. The corresponding comb modes beating with the laser were \(m_1=960542\) for the fundamental and \(m_2=1921085=2m_1+1\) for the second harmonic. The theoretical value of x was \(-1\). The beating frequencies between the lasers and the OFC were at the level of \(f_{b1}\sim 72\) MHz and \(f_{b2}\sim -56\) MHz.

Firstly, the \(f_{\mathrm {ref}}\) signal was generated and measured referred to the H-maser. A Symmetricom 3120A with 1-s sample interval (0.5 Hz measuring bandwidth, \(\Pi\) type filtering) was used to measure the frequency of \(f_{\mathrm {ref}}\). To examine the accuracy of the \(f_{\mathrm {ref}}\) generated, we measured the frequency of the 1560 nm laser by recording the frequencies of \(f_{\mathrm {CEO}}\), \(f_{\mathrm {r}}\) and \(f_{\mathrm {b1}}\) with the FXE counter at the same time. The measured \(f_{\mathrm {ref}}\) frequency and the numerically calculated value from beating frequencies were shown in Fig. 6a. The scaling factor k was \(14651567/2^{48}\) in this experiment. Linear fits were applied to the two data. The slopes of the data were \((1.158\pm 0.003)\times 10^{-9}\) Hz/s and \((1.16\pm 0.01)\times 10^{-9}\) Hz/s, and the offset frequencies were 9,999,999.864 565 07\(\pm 7\times 10^{-8}\) Hz and 9,999,999.864 565 05\(\pm 2.9\times 10^{-7}\) Hz, respectively. The Allan deviation of the \(f_{\mathrm {ref}}\)s were shown in Fig. 6b. These results showed that the \(f_{\mathrm {ref}}\) generated by RF processing and by numerical calculation met quite well. The main noise of the calculated \(f_{\mathrm {ref}}\) was limited by the precision of \(f_{\mathrm {r}}\) measurement. The drift of \(f_{\mathrm {ref}}\) was caused by the drift of the 1560 nm laser. The base line of the short term stability of the measured \(f_{\mathrm {ref}}\) was limited by the RF processing system, while the small bumps were caused by the H-Maser signal. The maser stood 6 floors higher than our lab and several RF distributors located in different rooms were cascadingly inserted between the maser and our system.

Fig. 6
figure 6

The frequency value of \(f_{\mathrm {ref}}\) referred to the H-maser. a \(f_{\mathrm {ref}}\) generated by RF processing (red), and numerically calculated from the reading of \(f_{\mathrm {r}}\), \(f_{\mathrm {CEO}}\) and \(f_{\mathrm {b1}}\) (blue). b The fractional Allan deviation of \(f_{\mathrm {ref}}\)s in (a)

Full size image
Fig. 7
figure 7

a The measured result of \(f_{\mathrm {diff}}\) referred to \(f_{\mathrm {ref}}\) (\(f_{\mathrm {dm}}\)). b The corresponding Allan deviation of R

Full size image

The \(f_{\mathrm {diff}}\) was generated according to the scheme shown in Fig. 2. The frequency of \(f_{\mathrm {diff}}\) was measured using the 3120A referred to \(f_{\mathrm {ref}}\). The measured frequency, i.e., the value of \(f_{\mathrm {dm}}\), was shown in Fig. 7a. This measurement lasted for 86400 s. The statistical result of \(f_{\mathrm {dm}}\) was

$$\begin{aligned} (10^7-1.1\times 10^{-9}) \pm 1.3\times 10^{-8}\text {~Hz}\,. \end{aligned}$$
(8)

Considering that the sign of x was negative, the corresponding ratio R was calculated to be

$$\begin{aligned} R=(2+1.2\times 10^{-22})\pm 1.4\times 10^{-21}\,. \end{aligned}$$
(9)

The Allan deviation of R was shown in Fig. 7b. The fractional instability of R was \(4.9\times 10^{-19}\) at averaging time of 1 s and \(1.9\times 10^{-21}\) at 1000 s. The dropping rate of the instability versus averaging time was \(1/\tau ^{0.8}\). After averaging time of 1000 s, the Allan deviation went flat, and reached \(1.4\times 10^{-21}\) at 10000 s. This was mainly due to the room temperature fluctuation. Similar phenomenon was observed in the TO test. This result suggested that the precision of the RF processing system might be further improved by stabilizing the temperature of the RF electronics.

Fig. 8
figure 8

The statistical values of \(R-2\) in different measurements

Full size image

To demonstrate the reliability of the RF processing system, several measurements were performed over one month. Each measurement lasted for half to one day. The obtained offset and corresponding statistical error were shown in Fig. 8. A weighted mean of \(-1.2\times 10^{-22}\) and weighted fractional uncertainty of \(2.4\times 10^{-21}\) were obtained. This result suggested that the RF processing system was reliable at the precision of \(10^{-21}\).

Because in this test the optical part of the system was in totally common mode, only performance of the RF system was tested, the precision would reduce when different branches of the OFC were used. To guarantee the precision of the OFR measurement, optical path stabilization could be introduced [25,26,27]. When the OFR measurement between optical clocks was carried out, the generated reference signal \(f_{\mathrm {ref}}\) could be used as the reference signal for the frequency shifting elements in the optical path to guarantee no additional frequency offset error was introduced.

4 Conclusion

In this work, we constructed a self-reference direct-measuring scheme for OFR measurement from the mathematical relation of laser frequencies and the OFC. According to the scheme, an RF processing system for OFR measurement was built. A precision of \(10^{-21}\) was obtained in a testing experiment, which was sufficient for OFR measurement of the state-of-the-art optical clocks. The scheme used only one single frequency counter in the final ratio measurement, which allowed more choice on frequency counters. This scheme could also be adapted for ultrastable laser generation by replacing the frequency counter in Fig. 2 with a phase locking loop to control the frequency of laser 2, thereby generating a stabilized laser with frequency equal to the frequency of the reference laser scaled by a preset ratio.