Numerical study of an efficient light focusing nano-coupler based on C-shaped waveguides

Abstract

We present an FDTD simulation study of a new design of light focusing nano-coupler consisting of a tapered succession of C-shaped silver waveguides. Its operation is based on the use of the fundamental guided mode $TE_{10}$. Thanks to the optimization of the structural design parameters, we have demonstrated numerically that this compact coupler enables a sub-wavelength light focusing with a transmission coefficient of 65% and a coupling efficiency of 77% that have higher values than the optimized designs reported in the literature. We also show that our structure is an efficient functional coupler at multiple wavelengths when used in a periodic grating as well as an isolated device. This could pave the way for the development of a new generation of metamaterials for guidance and detection applications.

1 Introduction

Photonic integrated circuits have greatly progressed in the last decade replacing the electronic ones, due to their unique ability to transport huge amounts of information over long distances. In this respect, they were developed to connect different optical devices achieving great improvements in rapidity, compactness and profitability [1, 2]. Studies show, however, that during the light transmission from an optical fiber at micrometer level to an integrated waveguide at nanometer level, very high losses occur because of the guiding properties mismatch existing between the two devices. Therefore, it turned out necessary to develop devices called couplers, which play the role of optical funnels. These are destined to concentrate the light coming from a large to a small area with minimum optical losses thus maximizing the performances of photonic devices such as detectors [3, 4], modulators [5, 6] and light emitting diodes [7, 8]. That is why there is a number of studies related to this topic [9, 10]. Depending on the employed physical approach, the developed nano-coupler devices could be divided in four major classes : direct couplers, tapered waveguides, lens couplers and scatterers. The simplest way is the direct coupling, in which the light is coupled first to a wide waveguide and then, with the help of a directional coupler, coupled into a smaller nano-waveguide. This kind of coupler which is based on end fire coupling [11, 12], resonant stub [13, 14] or arranging similar waveguides one next to or inside another [15,16,17], allows to achieve a large coupling efficiencies of about 70% but, since it requires preliminary coupler, the total coupling efficiency is reduced to 40%. The coupling phenomenon was also achieved using the tapered waveguides in which the light is compressed when propagating through the taper. The proposed optical funnel containing a metal-dielectric photonic crystal in [18] reaches only 13% of transmission and the tapered metallic wire proposed in [19] and experimentally fabricated in [20] shows a transmission of 20%. In addition, light could be tightly focused using dielectric lenses that achieve a maximal coupling efficiency of 45% [21] or plasmonic ones leading to a low transmission not exceeding 30% [22]. To achieve an effective coupling, other studies used scatterer couplers based on antennas or diffraction gratings. On the one hand, the antenna couplers exhibit a theoretical limit of 50% of the coupling efficiency due to the reradiation of the captured power back into free space [23]. Indeed, in the work [24], only a 10% coupling efficiency is reached at $\lambda =1550$ nm. On the other hand, the diffraction gratings exhibit high coupling efficiency up to 70% to the detriment of compactness because of their relatively large size [25, 26].

In this work, we propose a new design of a light focusing nano-coupler consisting of a tapered succession of silver C-shaped WaveGuides (CSWG$_s$). We start, in Section 2, by studying the influence of the different geometrical parameters of a CSWG on the cutoff wavelength of its $TE_{10}$ fundamental guided mode. In Section 3, we present the simulation results of the optimized coupler in the case of a periodic grating and as an isolated pattern.

2 Study of the $\mathbf {TE_{10}}$ fundamental mode of a CSWG

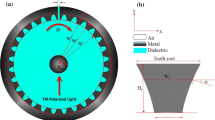
The scheme of a CSWG is shown in Fig. 1. It consists of a coaxial waveguide made of silver metal, having an outer radius $R_o$ and an inner radius $R_i$ with an additional metallic part controlled by the angle $\beta$. This structure was used for the conception of our couplers since the breaking of the revolution symmetry compared to the case of conventional coaxial waveguides enables the red shift of the cutoff wavelength allowing the realization of compact metamaterials exhibiting original properties such as negative refraction index [27] or artificial anisotropy [28]. Moreover, compared to other waveguide geometries, the C-shaped geometry allows the propagation of the optical signals over quite long distances of the order of several tens of micrometers without much attenuation via its $TE_{10}$ fundamental mode [29].

Fig. 1

Scheme of a silver CSWG having an inner radius $R_i$, an outer radius $R_o$ and a additional metallic part $\beta$

In this study, the numerical calculations were performed using the finite difference time domain (FDTD) algorithm previously developed [30]. FDTD is a numerical method to solve Maxwell’s equations, using spatial and temporal discretizations that allow determining the electromagnetic field [31]. Note that our homemade FDTD code was improved by integrating the Drude model to take better account of the metal dispersion [32,33,34]. Here, silver is preferred over other metals to reduce the propagation losses in the optical range. The structure eigen-modes and the corresponding eigen-values are then deduced from the resolution of the electromagnetic wave equation. First, as shown in [29], we confirmed that the fundamental guided mode of the CSWG is the $TE_{10}$ mode. This latter is similar to the fundamental mode of a rectangular-section waveguide and it is characterized by a lobe of E-field at its center. It is then perpendicularly polarized to the waveguide long sides (curved sides), therefore parallel to the axis of symmetry of the section. To do this, we calculated the spectral energy density of the structure [35, 36] depicted in Fig. 2, when $R_i = 140$ nm, $R_o = 240$ nm and $\beta = 177^{\circ }$. For these geometrical parameters, we get a cutoff wavelength of $\lambda _c=1550$ nm. The inset in Fig. 2 depicts the electric intensity distribution of the $TE_{10}$ mode at the cutoff. As it can be seen, the latter displays only one lobe of electric intensity which confirms the excitation of the $TE_{10}$ fundamental mode. It should be noted that, for the same radii, the CSWG handles guided mode with large value of wavelength compared to the conventional coaxial one. This opens the way for new perspectives in the device miniaturization and for enhanced transmission applications [29].

Fig. 2

Normalized energy density of a CSWG with $R_i = 140$ nm, $R_o = 240$ nm and $\beta = 177^{\circ }$. The inset shows the calculated electric intensity distribution (fifth root of the square modulus of the electric field) at the cutoff $\lambda _c=1550$ nm. The dashed lines underline the CSWG section

After that, we studied the influence of the geometrical parameters ($R_i, R_o$ and $\beta$) on the cutoff wavelength of the $TE_{10}$ fundamental mode. First, we vary the outer radius $R_o$ of a CSWG with fixed inner radius and additional metallic part ($R_i = 140$ nm and $\beta = 177^{\circ }$, respectively). When looking at Fig. 3a, one can see that, by varying $R_o$, the cutoff wavelength follows two different trends :

• Non-linear variation, when $R_o$ is close to $R_i$, due to the coupling between the two plasmonic metallic interface modes. This leads to an effective mode which penetrates more inside the metallic parts of the waveguide; thus, increasing the metallic losses.

• Linear variation, when $R_o$ is far from $R_i$, corresponding to the case in which the coupling between the two plasmonic metallic interfaces modes no longer happens.

Moreover, this behavior was already observed in the case of coaxial waveguides [37]. Then, the cutoff wavelength of the $TE_{10}$ mode was calculated as a function of $\beta$ when $R_i = 140$ nm and $R_o = 240$ nm. As illustrated in Fig. 3b, the cutoff wavelength decreases almost linearly with the increase of the additional metallic part size. Therefore, the cutoff wavelength of the $TE_{10}$ mode could be adjusted through the different geometrical parameters of the CSWG. This enables to control the cutoff of the different CSWG$_s$ that we will use to design our coupler device.

Fig. 3

Variation of the $TE_{10}$ cutoff wavelength as a function of : (a) The outer radius $R_o$ of a silver CSWG with $R_i = 140$ nm and $\beta = 177^{\circ }$. (b) The additional metallic part $\beta$ of a silver CSWG with $R_i = 140$ nm and $R_o = 240$ nm

3 Design of the light focusing coupler

Our sub-wavelength light focusing coupler, shown in Fig. 4, consists of a tapered succession of four CSWG$_s$ on which a gradual decrease on their radii is imposed leading to the following radii : CSWG$_1$ ($R_i=140$ nm, $R_o=240$ nm), CSWG$_2$ ($R_i=120$ nm, $R_o=220$ nm), CSWG$_3$($R_i=100$ nm, $R_o=200$ nm) and CSWG$_4$ ($R_i=80$ nm, $R_o=180$ nm). It should be noted that the different radii were picked to arrange the different metallic apertures one in front of another thus minimizing the reflections near the connection areas. Note that all the numerical calculations that will follow were performed by illuminating the coupler with a plane wave linearly polarized parallel to the CSWG’s axis-symmetry (here the x axis) and propagating along the z axis (see Fig. 4).

At the outset, to get all these CSWG$_s$ exhibiting the same cutoff wavelength at $\lambda =1550$nm, we proceeded to the optimization step using the following analytical formula [29] : $\lambda _c=2(\pi -\beta /2)(R_o+R_i)+\alpha$. This latter is only valid in the linear variation zone observed in Fig. 3a corresponding to outer radii far from the inner ones which is the case in our structures. $\alpha$ is the red-shift of the $TE_{10}$ fundamental mode cutoff due to the fact that our CSWG$_s$ are made of silver at which the light could penetrate unlike the case of a perfect electric conductor (PEC) at which the light is entirely reflected. The value of $\alpha =330$ nm is deduced from the previous formula using the geometrical parameters of the CSWG studied in Fig. 2 (with $R_i=140$ nm, $R_o=240$ nm and $\beta =177^{\circ }$ exhibiting a cutoff at $\lambda _c=1550$nm). After calculating the red-shift $\alpha$ and knowing the values of the different CSWG$_s$ radii, we calculate the size of the additional metallic part $\beta$ specific to each CSWG constituting the coupler. This optimization leads to the following geometrical parameters: CSWG$_1$ ($R_i=140$ nm, $R_o=240$ nm and $\beta =177^{\circ }$), CSWG$_2$ ($R_i=120$ nm, $R_o=220$ nm and $\beta =155^{\circ }$), CSWG$_3$($R_i=100$ nm, $R_o=200$ nm and $\beta =127^{\circ }$) and CSWG$_4$ ($R_i=80$ nm, $R_o=180$ nm and $\beta =90.2^{\circ }$). We confirmed the accuracy of these results, numerically, by calculating the cutoff corresponding to each CSWG taken separately which leads to equal cutoffs at $\lambda _c=1550$nm.

Fig. 4

Scheme of the proposed light focusing coupler having a height $h_{c} = 1000$ nm constituted by a tapered succession of four equal height CSWG$_s$

3.1 Study of the light focusing coupler as a periodic grating

First, we considered our coupler as a periodic grating of the pattern shown in Fig. 4 having a period $p=700$ nm along the x and y directions. This periodic arrangement enables the transmission enhancement since this latter is an individual effect (guided mode). The period of the grating is chosen so that the cutoff wavelength of the $TE_{10}$ fundamental mode is larger than the Rayleigh anomaly wavelength [38] given by : $\lambda _R= n\times p$ where n represents the substrate refractive index (in our case, $n=1$). To pick up the optimal coupler’s height ensuring the most efficient coupling, we fixed all the geometrical parameters of the grating coupler and we calculated the transmission coefficient (T) and the coupling efficiency (CE) corresponding to several coupler’s heights at $\lambda = 1550$ nm. The coupling efficiency is calculated by dividing the power flow calculated through the CSWG$_4$ section constituting the top of the coupler by the one calculated through the CSWG$_1$ section constituting the base of the coupler. Figs. 5a and b display the variation of the transmission coefficient (T) and the coupling efficiency (CE) respectively as a function of the grating coupler’s height ($h_c$). When looking to the latter, one can see that, from $h_c=500$ nm to $h_c=1500$ nm, the proposed grating coupler exhibits a good coupling performances reaching $T=65\%$ and $CE=77\%$. These original coupling properties come from the spatial compression of the $TE_{10}$ fundamental mode when propagating through the tapered succession of the CSWG$_s$ thanks to the appropriate proposed juxtaposition ensuring minimal losses. However, we can clearly notice that increasing the coupler’s height beyond $h_c=1500$ nm lowers the transmission coefficient and the coupling efficiency under 50% since the metallic losses increase when increasing the propagation length.

Fig. 5

(a) Transmission coefficient (T) and (b) coupling efficiency (CE) calculated as a function of the grating coupler’s height ($h_c$) having a period $p=700$ nm at $\lambda = 1550$ nm

In Fig. 6, we show the spectral variation of the power flows calculated considering a grating coupler with $p=700$ nm and $h_c=1000$ nm. $P_1$ is the power flow calculated through the CSWG$_1$ section constituting the base of the coupler and $P_4$ is the one calculated through the CSWG$_4$ section constituting the top of the coupler. These latters exhibit three different peaks at $\lambda =1550$ nm, $\lambda =1364$ nm and $\lambda =1050$ nm. So, in order to explain the origin of these three peaks, we mapped, in Fig. 7, the electric intensity distributions in the horizontal and vertical plans corresponding to each peak. On the one hand, we notice that the three xy electric intensity distributions (Figs. 7a,b and c) exhibit one lobe of electric intensity corresponding to the excitation of the $TE_{10}$ fundamental mode. On the other hand, the xz and the yz electric intensity distributions calculated at $\lambda = 1550$ nm show an uniform illumination due to the constant phase during the back and forth of the light propagation (See Figs. 7d and g). However, the xz and yz electric intensity distributions calculated at $\lambda = 1364$ nm and $\lambda = 1050$ nm depicted in Figs. 7(e, h) and (f, i), exhibit one and two intensity nodes corresponding to the first and the second harmonic of Fabry Perot resonances of the same $TE_{10}$ fundamental mode, respectively. Therefore, we are able to consider our proposed structure as an efficient coupler operating at various wavelength values which can be controlled by modifying the different geometrical parameters of the CSWG$_s$. In addition, Fig. 7 shows that the maximum electric intensity grows when propagating along the z axis which further emphasizes the efficiency of our coupler since it allows a quasi-conservation of the guided energy in each CSWG constituting the coupler.

Fig. 6

Spectral variation of the power flows calculated through the CSWG$_1$ section constituting the base ($P_1$) and through the CSWG$_4$ section constituting the top ($P_4$) of a grating coupler having $p=700$ nm and $h_c=1000nm$. The power flows depicted were normalized by the maximal value of $P_1$

Fig. 7

Electric intensity distributions (third root of the square modulus of the electric field) calculated in the horizontal plan xy (a, b and c) and the vertical plans xz (d, e and f) and yz (g, h and i) passing through the middle of the structure. The wavelength value is set to : $\lambda =1550$ nm in (a, d and g), $\lambda =1364$ nm in (b, e and h) and $\lambda =1050$ nm in (c, f and i). The grating coupler has the following geometrical parameters: $p=700$ nm and $h_c=1000$ nm

Fig. 8

(a) Transmission cross section ($T_c$) and (b) Coupling efficiency (CE) calculated as a function of the isolated coupler’s height ($h_c$) at $\lambda = 1553$ nm

Fig. 9

Spectral variation of the power flows calculated through the CSWG$_1$ section constituting the base ($P_1$) and through the CSWG$_4$ section constituting the top ($P_4$) of an isolated coupler having $h_c=1000$ nm. The power flows depicted were normalized by the maximal value of $P_1$

Fig. 10

Electric intensity distribution (third root of the square modulus of the electric field) of the isolated coupler having $h_c=1000$ nm calculated at $\lambda = 1553$ nm in the : (a) xy plan, (b) xz plan and (c) yz plan passing through the middle of the structure

3.2 Study of the light focusing coupler as an isolated pattern

In this part, to validate the efficiency of our coupler as an isolated structure, we consider only one coupler pattern (shown in Fig. 4) engraved into an infinite silver layer. Then, we calculated the variation of the coupling efficiency (CE) and the transmission cross section (T$_c$) as a function of the isolated coupler height ($h_c$) (See Fig. 8). The calculation of CE has been carried out following the same steps as in the periodic case. However, the transmission cross section has been calculated by dividing the power flow reaching the far field from the end of the coupler (in the z direction) by the one penetrating into the $CSWG_1$ section constituting the base of the coupler. It should be noted that instead of the transmission coefficient, the transmission cross section has been calculated in this part because, in the case of an isolated pattern, the transmission quantification is carried out, as is customary, by calculating its cross section. Moreover, considering the isolated coupler having ($h_c=1000$nm), we showed in Fig. 9 the power flows $P_1$ and $P_4$ (calculated through the CSWG$_1$ and CSWG$_4$ constituting the base and the top of the isolated coupler respectively) and we mapped in Fig. 10 the electric intensity distributions in horizontal and vertical plans at $\lambda = 1553$ nm. When comparing Fig. 5 with Fig. 8 and Fig. 6 with Fig. 9 and Figs. 7a, d and g with Figs. 10a, b and c, we can clearly notice that both the periodic grating coupler and the isolated one exhibit similar coupling behavior. All these results demonstrate that the proposed coupler operates at various wavelengths in both arrangements. The slight differences that might be noticed are due to the fact that in the periodic grating, we observe the coupling effect of several holes unlike the isolated pattern in which we see the effect of only one hole engraved in an infinite metallic layer [39, 40]. Moreover, as it is highlighted in Table 1, our proposed structure exhibits important coupling properties compared to the other coupling approaches previously reported in other studies.

Table 1 Comparison of the different coupling approaches with our proposed structure

4 Conclusion

In summary, we studied the excitation and the propagation of the $TE_{10}$ fundamental mode of a CSWG and showed, as expected, that its cutoff is highly sensitive to the different geometrical parameters. Then, we exploited the latter for designing an original optical coupler exhibiting a high sub-wavelength light focusing, at telecom wavelengths, with good transmission coefficient ($T=65\%$) and coupling efficiency ($CE=77\%$). Moreover, we demonstrated that in addition to being a functional structure, operating at several wavelengths, our proposed coupler shows efficient performances when arranged in a periodic grating as well as an isolated pattern. The future manufacturing of this type of structure will allow us to carry out a follow-up study to develop a novel generation of metamaterials for nano guiding, optical trapping and sensing applications.