1 Introduction

In 1998, Bender et al. [1, 2] discovered that non-Hermitian Hamiltonian with parity-time symmetry could have the real eigenvalue spectra. Further study of the non-Hermitian systems showed the existence of exceptional point (EP), where many interesting physical phenomena occur in classical optical systems [3,4,5,6,7,8,9,10,11,12,13], such as optical isolation [3], coherent perfect absorption [5], unidirectional reflectionlessness [8,9,10,11,12,13], electromagnetically induced transparency (EIT) [14], and so on.

Not only that, based on quantum systems of Hermitian [15,16,17,18,19] and non-Hermitian [20,21,22,23,24,25,26,27,28,29,30,31,32,33], transport properties of surface plasmon (SP) or photon in one-dimensional (1D) waveguide had been researched widely during the decade years. Especially, in non-Hermitian system, Chang et al. [20] studied the transport properties of SP based on the nanowire interacting with a two-level emitter. Chen et al. [23, 24] researched the transport properties of a single SP interacting with two quantum dots (QDs) coupled to a 1D waveguide. And Cheng et al. [25] analyzed the Fano-type transmission spectrum in a pair of semiconductor QDs coupled to a metal nanowire. In addition, Kim et al. [28] investigated the scattering properties of a SP by a two-level and a V-type three-level QDs coupling to a 1D waveguide. These studies mainly focused on the scattering properties for one direction. Recently, the non-Hermitian systems of plasmonic cavity coupled to the plasmonic waveguide (PW) have been employed to research on unidirectional reflectionlessness [34, 35]. Such as, based on the gain–loss [34] and loss–loss [35] plasmonic cavities coupled to a PW, Qiu et al. reported the single and dual-band unidirectional reflectionlessness, respectively. Besides, Wu et al. [36] investigated the dual-band unidirectional reflectionless phenomenon via the non-Hermitian system of three QDs coupled to a PW.

Motivated by the above ideas, we investigate the dual-frequency unidirectional reflectionless phenomenon at EPs in a non-Hermitian system, composed of a two-level and a V-type three-level QDs coupled to a PW, based on electromagnetically induced transparency-like effect. By appropriately adjusting the phase shift between two QDs, decay rates of the QDs, and coupling strengths between QDs and PW, the dual-frequency unidirectional reflectionlessness can be manipulated well.

2 Theoretical model

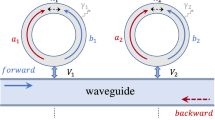
The non-Hermitian system composed of a two-level QD (denoted by \(\hbox {QD}_{{1}}\)) and a V-type three-level QD (denoted by \(\hbox {QD}_{{2}}\)) coupled to a PW is shown in Fig. 1. The effective non-Hermitian Hamiltonian can be given by (assuming \(\hbar\)=1)

$$\begin{aligned}&H=H_{W}+H_{Q}+H_{I}, \end{aligned}$$
(1)
$$\begin{aligned} H_{W}&=\int dx[ -iv_{g}c^{\dag }_{R}(x)\frac{\partial }{\partial x}c_{R}(x) \nonumber \\&\quad +iv_{g}c^{\dag }_{L}(x)\frac{\partial }{\partial x}c_{L}(x)], \end{aligned}$$
(2)
$$\begin{aligned} H_{Q}&=(\omega _{e}-\frac{i\Gamma _{1}}{2})\sigma _{ee}\nonumber \\&\quad +(\omega _{2}-\frac{i\Gamma _{2}}{2})\sigma _{22}\nonumber \\&\quad +(\omega _{3}-\frac{i\Gamma _{3}}{2})\sigma _{33}, \end{aligned}$$
(3)
$$\begin{aligned} H_{I}&=\int dx\delta (x)g_{1}\{[c^{\dag }_{R}(x)\nonumber \\&\quad +c^{\dag }_{L}(x)]\sigma _{ge}+[c_{R}(x)+c_{L}(x)]\sigma _{eg}\}\nonumber \\&\quad +\int dx\delta (x-d)g_{2}\{[c^{\dag }_{R}(x)\nonumber \\&\quad +c^{\dag }_{L}(x)]\sigma _{12}+[c_{R}(x)+c_{L}(x)]\sigma _{21}\}\nonumber \\&\quad +\int dx\delta (x-d)g_{3}\{[c^{\dag }_{R}(x)+c^{\dag }_{L}(x)]\sigma _{13}\nonumber \\&\quad +[c_{R}(x)+c_{L}(x)]\sigma _{31}\}, \end{aligned}$$
(4)

where \(H_{W}\), \(H_{Q}\) and \(H_{I}\) represent the Hamiltonians of SP propagation in PW, two QDs and interaction between two QDs and PW, respectively. Here, \(c^{\dag }_{R(L)}(x)\) and \(c_{R(L)}(x)\) denote the creation and annihilation operators of a right-going (left-going) SP in PW at x, respectively. \(\omega _{e}\) (\(\omega _{2}\), \(\omega _{3}\)) and \(\Gamma _{1} (\Gamma _{2}, \Gamma _{3})\) are the transition frequency and decay rate of \(\hbox {QD}_{1(2)}\), respectively. And \(g_{1}\) (\(g_{2}\), \(g_{3}\)) is the coupling strength between the PW and \(\hbox {QD}_{1(2)}\). In addition, \(\sigma _{ee}=|e\rangle \langle e|\), \(\sigma _{22}=|2\rangle \langle 2|\) and \(\sigma _{33}=|3\rangle \langle 3|\) represent the diagonal elements. \(\sigma _{eg}=|e\rangle \langle g|\) (\(\sigma _{ge}=|g\rangle \langle e|\)) is the raising (lowering) operator of \(\hbox {QD}_{{1}}\), and \(\sigma _{21}=|2\rangle \langle 1|, \sigma _{31}=|3\rangle \langle 1|\) (\(\sigma _{12}=|1\rangle \langle 2|\), \(\sigma _{13}=|1\rangle \langle 3|\)) are the raising (lowering) operators of \(\hbox {QD}_{{2}}\), respectively.

Fig. 1
figure 1

Schematic diagram of a PW coupled to a two-level QD and a V-type three-level QD with a separation distance d

Full size image

We assume that the energy of a SP incident from the left or right is given by \(E_{k}=v_{g}k\) with \(v_{g}\) as the group velocity of the incident SP of wave vector k. So, the eigenstate of the composite system can be expressed as

$$\begin{aligned} |E_{k}\rangle= & {} \int dx[\phi _{f}(x)c^{\dag }_{R}(x)\ +\phi _{b}(x)c^{\dag }_{L}(x)]|0,g,1\rangle \nonumber \\&+\varepsilon _{1}|0,e,1\rangle +\varepsilon _{2}|0,g,2\rangle +\varepsilon _{3}|0,g,3\rangle , \end{aligned}$$
(5)

where \(|0,g,1\rangle\) denotes no SP in PW and two QDs are in ground states. \(\varepsilon _{{1}}\) and \(\varepsilon _{{2}({3})}\) are the excitation amplitudes that the two-level QD and three-level QD absorb a SP and jump to the excited states \(|e\rangle\) and \(|2\rangle\) (\(|3\rangle\)), respectively. For a single SP incident from the forward and backward directions, the scattering amplitudes \(\phi _{f}(x)\) and \(\phi _{b}(x)\) can be written as \(\phi _{f}(x)=e^{ikx}[\theta (-x)+a\theta (x)\theta (x-d)+t\theta (x-d)]\) and \(\phi _{b}(x)=e^{-ikx}[r\theta (-x)+b\theta (x)\theta (d-x)]\), where \(\ t\) and r are the transmission and reflection coefficients, respectively. \(e^{ikx}[a\theta (x)\theta (x-d)]\) and \(e^{-ikx}[b\theta (x)\theta (d-x)]\) are wave functions of SP between two QDs. \(\theta (x)\) is the Heaviside step function. When \(x\ge 0\) and \(x<0\), \(\theta (x)\) is equal to 1 and 0, respectively.

3 Results and discussion

For simplicity, we choose the decay rates of two QDs as \(\Gamma _1\)=\(\Gamma _{{2}({3})}\)=\(\Gamma\) and the coupling strengths between QDs and PW as \(g_{1}\) = \(g_{{2}({3})}\) = g. So, by solving the eigenvalue equation \(H|E_{k}\rangle =E_{k}|E_{k}\rangle\), transmission and reflection coefficients for forward and backward directions can be expressed as

$$\begin{aligned} t&=t_{f}=t_{b}=\frac{(\Gamma -2i\delta _{1})(\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3}) }{P}, \end{aligned}$$
(6)
$$\begin{aligned} r_{f}&=-\frac{Q+4\eta [-(\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3})+2e^{2i\theta }(i\Gamma +2i\delta _{1})(i\Gamma +\delta _{2}+\delta _{3})]}{M}, \end{aligned}$$
(7)
$$\begin{aligned} r_{b}&=-\frac{Q-4\eta [2(\Gamma -2i\delta _{1})(\Gamma -i\delta _{2}-i\delta _{3})+e^{2i\theta }(\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3})]}{M}, \end{aligned}$$
(8)

where \(\delta _{1(2,3)}=\omega -\omega _{e(2,3)}\), \(\eta ={g^{2}}/{v_{g}}\), \(P={32\eta ^2(\Gamma -i\delta _{2}-i\delta _{3})+4\eta (\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3})}+8\eta (\Gamma -2i\delta _{1})(\Gamma -i\delta _{2}-i\delta _{3})+(\Gamma -2i\delta _{1})(\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3})+32i\eta ^2e^{2i\theta }(i\Gamma +\delta _{2}+\delta _{3})\nonumber ,\) \(Q=32\eta ^2(-1+e^{2i\theta })(\Gamma -i\delta _{2}-i\delta _{3})\), \(M=Q-(\Gamma -2i\delta _{1})(\Gamma -2i\delta _{2})(\Gamma -2i\delta _{3})+4\eta [-3\Gamma ^2+4i\Gamma (\delta _{1}+\delta _{2}+\delta _{3})+4(\delta _{1}\delta _{2}+\delta _{2}\delta _{3}+\delta _{1}\delta _{3})]\nonumber ,\) and \(\theta =kd\) is the phase shift between two QDs. Here, \(T=|t|^{2}\), \(R_{f}=|r_{f}|^{2}\) and \(R_{b}=|r_{b}|^{2}\) denote the transmission, forward and backward reflections, respectively.

Figure 2a and b show the transmission and reflection spectra versus frequency of the incident SP. The solid lines are the transmission and reflection spectra in the case of only a V-type three-level QD coupled to a PW versus frequency with different coupling strengths \(0.5\eta\), \(\eta\) and \(1.5\eta\). From Fig. 2a, the narrow transmission windows appear at around \(1.224\times 10^{15}~\mathrm {rad/s}\) and transmission increases with increasing the coupling strength. That is, EIT-like phenomenon occurs in the case of a three-level QD coupled to a PW, which induces two new resonance modes at around \(1.2393\times 10^{15}~\mathrm {rad/s}\) and \(1.2075\times 10^{15}~\mathrm {rad/s}\), respectively. And the dotted lines in Fig. 2 are the transmission and reflection spectra when only a two-level QD couples to a PW. The resonance frequency is around \(1.2280\times 10^{15}~\mathrm {rad/s}\) between two resonance modes of the EIT-like effect.

Fig. 2
figure 2

Transmission and reflection spectra versus frequency of incident SP when only one QD couples to the PW. Here, the decay rate is \(\Gamma =0.056~\eta\) with \(\eta =2.168\times 10^{13}\) rad/s

Full size image

Figure 3 shows the transmission and reflection spectra versus frequency of the incident SP when phase shift \(\theta =0.958\pi\) between two QDs. In Fig. 3, the black and red dash lines represent the reflection spectra for forward and backward directions, respectively. Clearly, reflections for forward (backward) direction are \(\sim\) 0 (\(\sim\) 0.93) and \(\sim\) 0.59 (\(\sim\) 0) at frequencies \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\), respectively. And the transmission spectra (blue solid line) for forward and backward directions are the same. That is, dual-frequency unidirectional reflectionless phenomenon occurs at frequencies \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\), when phase shift \(\theta =0.958~\pi\).

Fig. 3
figure 3

Transmission and reflection spectra for forward and backward directions versus frequency when phase shift \(\theta =0.958~\pi\). The decay rate is \(\Gamma =0.056~\eta\) with \(\eta =2.168\times 10^{13}\) rad/s

Full size image

Here, we assume that the phase shift of the two-level QD is denoted by \(\phi _{1}\) and that of the low (high)-energy mode of the EIT-like effect induced by V-type three-level QD is \(\phi _{2}\) (\(\phi '_{2}\)). Accordingly, the total phase differences \(\phi _{all}\) and \(\phi '_{all}\) for forward (backward) direction can be expressed [35,36,37,38] as \(\phi _{all}=\phi _{1 (2)} - \phi _{2(1)} + 2\theta\) and \(\phi '_{all}\) = \(\phi _{1}('_{2}) - \phi '_{2}(_{1}) + 2\theta\) with \(\theta\) the phase shift of SP propagation between two QDs. The phase difference \(\phi _{all}\) (\(\phi '_{all}\)) is close to 2\(\pi\) when \(\theta =0.958\pi\) for forward (backward) direction, which results in the reflection for forward (backward) direction approaching 0 based on Fabry–Perot resonance coupling. That is to say, dual-frequency unidirectional reflectionlessness is obtained in our system.

Then, we investigate the physical properties of the non-Hermitian quantum system using scattering matrix. According to Eqs. (6), (7) and (8), the scattering matrix S of the non-Hermitian system can be described by

$$\begin{aligned} S= \left( \begin{array}{cc} t &{} r_{b} \\ r_{f} &{} t \\ \end{array} \right) . \end{aligned}$$
(9)

From Eq. (9), the corresponding eigenvalues of scattering matrix S are

$$\begin{aligned} s_{\pm } = t \pm \sqrt{r_{f}r_{b}}. \end{aligned}$$
(10)

When \(\sqrt{r_{f}r_{b}}=0\) ( \(r_{b}=0\), \(r_{f}\ne 0\) or \(r_{f}=0\), \(r_{b}\ne 0\) ), two eigenvalues \(s_{\pm }\) coalesce and EPs occur. That is to say, unidirectional reflectionless phenomenon appears at EPs.

Next, based on Eq. (10), the real and imaginary parts curves of the eigenvalues \(s_{\pm }\) as a function of frequency when \(\theta =0.958\pi\) are depicted in Fig. 4a and b, respectively. From Fig. 4a and b, we find that two real parts of eigenvalues \(s_{\pm }\) coalesce with each other and two imaginary parts cross at two frequency points of \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\), respectively. The results indicate that the same complex eigenvalues \(s_{+}=s_{-}\) occur at \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\), respectively. In other word, EPs occur at \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\) when phase shift \(\theta =0.958\pi\). In this case, t is complex and \(\sqrt{r_{f} r_{b}}\) is zero. Hence, dual-frequency unidirectional reflectionlessness can be realized at two EPs when the phase shift \(\theta =0.958\pi\) between two QDs.

Fig. 4
figure 4

Real (a) and imaginary (b) parts of the eigenvalues \(s_{\pm }\) of the scattering matrix S as the function of frequency when phase shift \(\theta =0.958~\pi\)

Full size image

To research the effect of the phase shift \(\theta\) between two QDs on reflection, we plot the reflections for forward and backward directions versus phase shift and frequency in Fig. 5a and b, respectively. Obviously, the low reflection regions for forward direction around frequency ranges of \(1.2352\times 10^{15}~\mathrm {rad/s}\) \(\sim\) \(1.2401\times 10^{15}~\mathrm {rad/s}\) and \(1.2091\times 10^{15}~\mathrm {rad/s}\) \(\sim\) \(1.2161\times 10^{15}~\mathrm {rad/s}\) in Fig. 5a, respectively, correspond to high reflection regions for backward direction in Fig.  5b. And the low reflection region for backward direction (Fig.  5b) around frequency range of \(1.2138\times 10^{15}~\mathrm {rad/s}\) \(\sim\) \(1.2320\times 10^{15}~\mathrm {rad/s}\) corresponds to high reflection region for forward direction (Fig. 5a). As a consequence, dual-frequency unidirectional reflectionlessness can be realized in the wide frequency ranges.

Fig. 5
figure 5

Dependencies of reflections for forward (a) and backward (b) directions on phase shift \(\theta\) between two QDs and frequency. The decay rate is \(\Gamma =0.056~\eta\) with \(\eta =2.168\times 10^{13}\) rad/s

Full size image

Then we discuss the effects of decay rates of two QDs and frequency of the incident SP on reflections for forward and backward directions with phase shift \(\theta =0.958~\pi\). It’s worth nothing that the low reflection region for forward (backward) direction in Fig. 6(a) (6(b)) in the range of decay rates from \(\sim\) \(0.075\times 10^{13}\) rad/s to \(\sim\) \(0.562\times 10^{13}\) rad/s and frequency around \(1.2385\times 10^{15}~\mathrm {rad/s}\) (\(1.2171\times 10^{15}~\mathrm {rad/s}\)) corresponds to high reflection region for backward (forward) direction in Fig. 6(b) (6(a)). As a consequence, dual-frequency unidirectional reflectionlessness can be realized in the wide range of decay rate when phase shift \(\theta =0.958\pi\).

Fig. 6
figure 6

Dependencies of reflections for forward (a) and backward (b) directions on decay rates \(\Gamma\) of two QDs and frequency when phase shift \(\theta =0.958\pi\) and \(\eta =2.168\times 10^{13}\) rad/s

Full size image

Lastly, we analyze the effects of frequency and coupling strengths between the PW and two QDs on reflections for forward and backward directions when \(\theta =0.958~\pi\) and \(\Gamma =0.056~\eta\). According to Fig. 7, low reflection regions have the red shifts with increasing the coupling strengths \(\eta\). Morever, low reflection region for forward (backward) direction in Fig. 7(a) (7(b)) in range of coupling strengths from \(\sim\) 0.0296\(\times 10^{13}\) rad/s (\(\sim\) 0.01552\(\times 10^{13}\) rad/s) to \(\sim\) 0.1191\(\times 10^{13}\) rad/s (\(\sim\) 0.0515\(\times 10^{13}\) rad/s) around the frequency \(1.2385\times 10^{15}~\mathrm {rad/s}\) (\(1.2171\times 10^{15}~\mathrm {rad/s}\)) corresponds to high reflection region for backward (forward) direction in Fig. 7(b) (7(a)). Therefore, dual-frequency unidirectional reflectionlessness can be achieved in the wide range of coupling strengths. Besides, unidirectional reflectionless phenomenon will disappear if the coupling strengths between the PW and QDs are smaller than the critical value 0.01552\(\times 10^{13}\) rad/s.

Fig. 7
figure 7

Dependencies of reflections for forward (a) and backward (b) directions on the coupling strengths \(\eta\) and frequency when phase shift \(\theta =0.958\pi\) and decay rate \(\Gamma =0.056\eta\)

Full size image

4 Conclusion

We have demonstrated the dual-frequency unidirectional reflectionlessness in a non-Hermitian system of two different energy-level QDs coupled to a PW based on electromagnetically induced transparency-like effect. By appropriately adjusting the phase shift between two QDs, decay rates of two QDs, and coupling strengths between the QDs and PW, the dual-frequency unidirectional reflectionlessness can be realized at EPs with the frequency \(1.2385\times 10^{15}~\mathrm {rad/s}\) and \(1.2171\times 10^{15}~\mathrm {rad/s}\). Moreover, the dual-frequency unidirectional reflectionlessness can be implemented in a wide ranges of decay rates and coupling strengths. We believe that our research will have the potential applications in design of plasmonic quantum devices, single SP switching, and so on.