1 Introduction

Referring to the important and widespread role of entanglement in quantum mechanics [1], especially in quantum information theory [2,3,4,5,6,7,8,9], many attempts have been made to produce entangled states over the past decades. This phenomenon briefly indicates a kind of correlation between two or more sub-systems and it can also be produced by correlating different degrees of freedom of the system. Many researchers have introduced different types of entangled states of two or more modes and studied their properties by analyzing criteria, such as the quantum statistics, second-order correlation function, quadrature squeezing, photon statistics, polarization, entanglement, and so on. For instance, the entanglements of photons of two-mode coherent states [10,11,12,13,14,15,16], two-mode squeezed states [17,18,19,20], two-mode cat states [21, 22], two-mode pair-coherent states and Perelomov coherent states [23], two-mode nonlinear coherent states [24], entangled state involving linear momentum and polarization degrees of freedom [25, 26], entanglement generation of the orbital angular momentum as another degree of freedom of the radiation field [27,28,29,30,31,32,33,34], three mode even coherent states [35] were discussed and analyzed in more details.

Recently, Karimi et al. introduced new types of entangled coherent-squeezed states (ECSS), and studied some of their nonclassical properties [36]. They used a theoretical scheme based on the interaction between a \(\Lambda\)-type three-level atom and a two-mode quantized field to generate the entangled states. In continuation, to achieve new entangled states with different and controllable nonclassical features, they introduced two-mode photon-added ECSS and study some of their nonclassical properties [37]. They realized a feasible experimental setup to generate the superpositions of two mode photon-added ECSS, too. The authors showed how they can achieve rich non-classical states by adding photons to the coherent mode of the ECSS. The introduced ECSS can particularly be useful, for instance, to realize quantum metrology [38, 39] and quantum clock synchronization [40, 41]. On the one hand, we know that adding or subtracting photons is one of the ways to non-linearize coherent states, which mainly leads to increasing non-classical features [42, 43]. On the other hand, photon-added coherent states are a special category of nonlinear coherence states (NLCS), \(|\alpha ,f\rangle\) with a special nonlinear function, f, that have been introduced and studied in various literature. To gain insight into the effectiveness of the NLCS in quantum information theory, we introduced two-qutrit entangled NLCS with different selection of the nonlinearity function f [44]. We found that depending on the chosen nonlinearity function, one can observe different nonclassical effects. Also, the control role of the nonlinearity function on the entanglement and statistical properties of the system state was investigated. Hence, our main motivation is to examine the effect of different selection of nonlinearity functions in the ECSS, where the coherent state of which will be replaced by the NLCS, and expect to improve non-classical features by choosing an appropriate NLCS.

Obviously, \(|\alpha ,f\rangle\) becomes the canonical coherent state when f becomes unity. The Fock space representation of the NLCS is explicitly given by \(|\alpha ,f\rangle \equiv \sum _{n=0}^{\infty }\frac{\alpha ^{n}}{\sqrt{n!}[f(n)]!}|n\rangle\), where we set \([f(n)]!=f(1)f(2)\ldots f(n), [f(0)]!=1\). It is worth noting that among the many NLCS mentioned in Refs. [23, 45,46,47,48,49,50,51,52,53,54], we focus only on a special and limited number of the NLCS with specific nonlinearity functions that have been physically realized [55,56,57,58,59,60,61,62,63,64,65,66,67]. Here, we focus on a special nonlinear coherent states with the corresponding nonlinearity functions as follows:

  • \(f_\mathbf{h }=\frac{1}{\sqrt{n}}\), subscript ‘h’ refers to the states already discussed as the Harmonious states [55]. By choosing the parameter \(\alpha = 0\) and 1, the state \(|\alpha ,f\rangle _\mathbf{h }\) becomes the ground state of a simple harmonic oscillator and the number-phase state [56], respectively. Superpositions of two qubit-type entangled coherent states [24, 42], photon-added two-mode entangled harmonious states [68], photon-subtracted entangled harmonious states [43], and two-mode qutrit-like entangled coherent states [44] have been widely considered in the literature, where each subsystem is spanned by two linearly independent harmonious states.

  • \(f_\mathbf{v }=\frac{L^{1}_{n}(|\eta |^2)}{(n+1)L^{0}_{n}(|\eta |^2)}\), in which \(|\eta |^2\) being the Lamb–Dicke parameter, \(L^{m}_{n}\)’s are the associated Laguerre polynomials. Such states may appear as stationary states of the center-of-mass motion of a trapped and bi-chromatically laser-driven ion far from the Lamb–Dicke regime [47]. Several superpositions of two-mode qubit-like NLCSs of trapped ion were introduced in Ref. [68], and their nonclassical properties were studied.

  • \(f_\mathbf{y }=\sqrt{1-\frac{\chi }{\nu }(1-n^{k-1})}\): As another case of nonlinear system, one may consider a deformed oscillator described by \(f_\mathbf{y }(n)\) in which the parameter \(\chi\) is an anharmonicity parameter (\(0<\chi <\nu\)) and k is an integer such that \(k>1\). This system corresponds to the an-harmonic oscillator model studied by Yurke and Stoler [69], and has attracted many interests in quantum optics [70], as well as the quantum information theory [71]. For the particular case with \(k = 2\), the deformed Hamiltonian corresponds with the field becomes the Kerr Hamiltonian [72]. In this regard, enhancing entanglement of entangled coherent states via a f-deformed photon-addition operation, and choosing a particular deformation function \(f_\mathbf{y }(n)\) was well studied in Ref. [73].

  • \(f_\mathbf{a }=1-\frac{m}{1+n}\): As an interesting class of NLCS of light, the so-called photon-added coherent states (PACSs), they are introduced by Agarwal et al. [53], and Zavat et al. [74] reported the experimental generation of single-PACSs. These states can be approximately generated in the laboratory by conditional measurement in the Jaynes–Cummings dynamics, in a beam splitter output, or in the spontaneous parametric down-conversion [75, 76]. The addition of photons to the two-mode qubit(qutrit)-like entangled states to enhance their non-classical features has been introduced and discussed in various Refs. [24, 42, 43, 73, 77, 78].

  • \(f_\mathbf{w }=1+\lambda \left[ \frac{1-(-1)^n}{n}\right]\), with \(\lambda =\frac{p-1}{2}\) and p as the para-Bose order this implies the para-Bose systems [78]. The effects of parity-deformed fields on the quantum statistical properties [79,80,81,82,83,84], and the dynamics of entanglement transfer to distant noninteracting atomic qubits was discussed in Ref. [85]. The parity-deformation of the quantum harmonic oscillator is used to describe the generalized Jaynes–Cummings model, in which the maximally entangled states may emerge [86]. Quantum simulation of the para-Bose systems was proposed by Alderete et al. [87, 88] such that highly entangled vibrational and internal ion states are achieved.

This paper is organized as follows: in Sect. 2, we construct new normalized superposition of the two-mode ENCSS associated to the simple-harmonic oscillator. In Sect. 3, we study some of their non-classical properties such as the sub-Poissonian statistics, and quantum polarization in terms of different nonlinearity functions. In Sect. 4, we will measure the amount of entanglement of the introduced states using concurrence criterion, and finally in Sect. 5, we conclude the results.

2 An overview of the ENCSS

Following earlier works on entangled coherent-squeezed states [36, 37], we introduce the ENCSS in two different groups, consist of non-linear coherent states and even(odd)-squeezed states as follows

$$\begin{aligned}&|\Psi , f\rangle _{e}=A_{e}\left[ |\alpha , f\rangle |-\xi \rangle _{e}+|-\alpha , f\rangle |\xi \rangle _{e}\right] , \end{aligned}$$
(1a)
$$\begin{aligned}&|\Psi , f\rangle _{o}=A_{o}\left[ |\alpha , f\rangle |-\xi \rangle _{o}+|-\alpha , f\rangle |\xi \rangle _{o}\right] , \end{aligned}$$
(1b)

where the parameter \(\alpha\) and nonlinearity function f are assumed similar in the two modes of introduced states. The notations \(|\xi \rangle _{e(o)}\) and \(|\alpha , f\rangle\) used instead of even(odd) squeezed states and the NLCS:

$$\begin{aligned}&|\pm \xi \rangle _{e}=N_{e}\sum ^{\infty }_{k=0}{(\mp 1)^k\frac{\sqrt{(2k)!}}{2^{k}k!}\left( e^{i\theta }\tanh r\right) ^k}|2k\rangle , \end{aligned}$$
(2a)
$$\begin{aligned}&|\pm \xi \rangle _{o}=N_{o}\sum ^{\infty }_{k=0} (\mp )^k\frac{2^{k}k!}{\sqrt{(2k+1)!}} \nonumber \\&\qquad \left( e^{i\theta }\tanh r\right) ^k |2k+1\rangle , \end{aligned}$$
(2b)
$$\begin{aligned}&|\pm \alpha ,f\rangle =N_{f}\sum _{k=0}^{\infty }(\pm 1)^k\frac{\alpha ^{k}}{\sqrt{k!}[f(k)]!}|k\rangle , \end{aligned}$$
(2c)

where \(\xi =\alpha =re^{i\theta }\) are two complex parameters, such that \(|\alpha |\) and \(|\xi |\) have been considered the same and equal to r and their phase \(\theta\), has been supposed to be zero. The normalization coefficients \(A_{e(o)}\), \(N_{e(o)}\) and \(N_{f}\) are calculated as follows:

$$\begin{aligned} A_{e}&=\mathcal {N}^{-1}_{e}\mathcal {N}^{-1}_{f} \nonumber \\&\qquad \left( \sum ^{\infty }_{k=0}{\sum ^{\infty }_{k'=0}{\left( 2+2(-1)^{k+k'}\right) \frac{r^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^{2}}\frac{{(2k')!}}{2^{2k'}(k'!)^2}}}\right) ^{-1/2}, \end{aligned}$$
(3a)
$$\begin{aligned} A_{o}&=\mathcal {N}^{-1}_{o}\mathcal {N}^{-1}_{f} \nonumber \\&\qquad \left( \sum ^{\infty }_{k=0}{\sum ^{\infty }_{k'=0}{\left( 2+2(-1)^{k+k'}\right) \frac{r^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^{2}}\frac{{2^{2k'}(k'!)^2}}{(2k'+1)!}}}\right) ^{-1/2}, \end{aligned}$$
(3b)
$$\begin{aligned} \mathcal {N}_{e}&=\left( \sum ^{\infty }_{k=0}{\frac{(2k)!}{2^{2k}(k!)^2}\left( \tanh r\right) ^{2k}}\right) ^{-1/2}, \end{aligned}$$
(3c)
$$\begin{aligned} \mathcal {N}_{o}&=\left( \sum ^{\infty }_{k=0}{\frac{2^{2k}(k!)^2}{(2k+1)!}\left( \tanh r\right) ^{2k}}\right) ^{-1/2}, \end{aligned}$$
(3d)
$$\begin{aligned} \mathcal {N}_{f}&=\left( \sum _{k=0}^{\infty }\frac{r^{2k}}{k!([f(k)]!)^2}\right) ^{-1/2}. \end{aligned}$$
(3e)

According to the above assumptions, the ENCSS can be written as a series expansion of the Fock basis, i.e.

$$\begin{aligned}&|\Psi , f\rangle _{e}=A_{e}\mathcal {N}_{e}\mathcal {N}_{f}\sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( (-1)^k+(-1)^{k'}\right) \frac{r^{k}\left( \tanh r\right) ^{k'}}{\sqrt{k!}[f(k)]!}\frac{\sqrt{(2k')!}}{2^{k'}k'!}}|k\rangle \otimes |2k'\rangle , \end{aligned}$$
(4a)
$$\begin{aligned}&|\Psi , f\rangle _{o}=A_{o}\mathcal {N}_{o}\mathcal {N}_{f}\sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( (-1)^k+(-1)^{k'}\right) \frac{r^{k}\left( \tanh r\right) ^{k'}}{\sqrt{k!}[f(k)]!}\frac{2^{k'}k'!}{\sqrt{(2k'+1)!}}}|k\rangle \otimes |2k'+1\rangle , \end{aligned}$$
(4b)

which will be very useful for future calculations.

3 Statistical properties of the ENCSS

In this subsection, we shall proceed to investigate some of the nonclassical properties of the states \(|\Psi , f\rangle _{e(o)}\) given in Eqs. (1a, 1b). For this reason, we will calculate and analyze some quantities including photon statistics through Mandel’s parameter, quantum polarization using the Stokes parameters and study the amount of entanglement of the introduced ENCSS by evaluating concurrence. It is worth noting that due to the presence of nonlinearity function,f, calculation of the statistical quantities is too long and really complicated, which we will see in Eqs. 6a–d and 12a–c. For this reason, it is not possible to calculate statistical quantities analytically, and then we show here the results of numerical analysis by drawing some figures. Throughout this paper, we have assumed that the parameter \(|\alpha |\) is any positive value, exceptionally for the case of the harmonious state where we put \(|\alpha | \in (0, 1)\). For this reason, in some cases, we have drawn diagrams related to this mode separately from the others.

  • Sub-Poissonian Photon Statistics

Here we study the photon-number statistics of the ENCSS, by employing Mandel’s parameter defined as:

$$Q_{i}^{{|\psi ,f\rangle _{{e(o)}} }} : = \frac{{\langle N_{i}^{2} \rangle _{{f,e(o)}} - \langle N_{i} \rangle _{{f,e(o)}}^{2} }}{{\langle N_{i} \rangle _{{f,e(o)}} }} - 1,\quad i = 1,2.$$
(5)

The different values of Mandel’s parameter indicate a special type of deviation of the photon number distribution from the Poissonian statistics \(Q=0\). A field is included non-classical property if \(Q < 0 (> 0)\) which are related to sub(super)-Poissonian photon statistics, respectively. It is clear that, analysis of Mandel’s parameter of the first or the second modes is subject to calculate the expectation values of the number operator \(N_{i}(=a^{\dag }_{i}a_{i})\) and its square for the ENCSS, where we have

$$\begin{aligned}&\langle N_{1}\rangle _{f, e}=|A_{e}\mathcal {N}_{e}\mathcal {N}_{f}|^2\sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( 2+2(-1)^{k+k'}\right) \frac{kr^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^2}\frac{{(2k')!}}{2^{2k'}(k'!)^2}}, \end{aligned}$$
(6a)
$$\begin{aligned}&\langle N_{2}\rangle _{f, e}=|A_{e}\mathcal {N}_{e}\mathcal {N}_{f}|^2 \sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( 2+2(-1)^{k+k'}\right) \frac{r^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^2}\frac{{2k'(2k')!}}{2^{2k'}(k'!)^2}}, \end{aligned}$$
(6b)
$$\begin{aligned}&\langle N_{1}\rangle _{f, o}=|A_{e}\mathcal {N}_{o}\mathcal {N}_{f}|^2 \sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( 2+2(-1)^{k+k'}\right) \frac{kr^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^2}\frac{{2^{2k'}(k'!)^2}}{(2k'+1)!}}, \end{aligned}$$
(6c)
$$\begin{aligned}&\langle N_{2}\rangle _{f, o}=|A_{e}\mathcal {N}_{o}\mathcal {N}_{f}|^2 \sum ^{\infty }_{k=0} \sum ^{\infty }_{k'=0} \nonumber \\&\qquad {\left( 2+2(-1)^{k+k'}\right) \frac{r^{2k}\left( \tanh r\right) ^{2k'}}{k!([f(k)]!)^2}\frac{{2^{2k'}(2k'+1)(k'!)^2}}{(2k'+1)!}}. \end{aligned}$$
(6d)

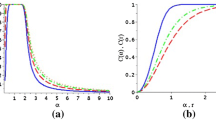
In Figs. 1 and 2, variations of Mandel’s parameter associated with these states as well as the first and the second modes have been presented and compared in terms of r and the nonlinearity functions f, respectively. As Fig. 1 shows, Mandel’s parameter of the first mode \(i=1\) displays same behavior for both of the states \(|\psi , f\rangle _{e(o)}\); however, the choice of nonlinearity function plays a very decisive role in the existence of the sub-Poissonian statistics. Comparing with the nonlinearity function of the photon-add coherent state, choosing nonclassical states with the nonlinearity functions of \(f_{\text {h}}\) and \(f_{\text {y}}\) results in the highest negative values for Mandel’s parameter. In other words, one can find some wide regions in which these states include fully sub-Poissonian statistics. Choosing the nonlinearity function \(f_{\text {v}}\) a result similar with the photon-added states is archived. Also, by preparing the field of the first mode in one of the standard coherent or the \(\lambda\)-deformed coherence states, we reach a fully super-Poissonian statistics for small values of r. Another point that Fig. 1 shows is related to the large values of r in which Mandel’s parameter of the photon-added and the \(\lambda\)-deformed coherent states tend to zero, while all the states with nonlinearity functions \(f_{\text {h,y,v}}\) remain non-classical with sub-Poissonian statistics. Calculating Mandel’s parameter of the even and odd states \(|\psi , f\rangle _{e(o)}\) of the second mode \(i=2\) emerges completely different results such that the odd state \(|\psi , f\rangle _{o}\) includes sub-Poisson statistics for small values of r, while the other one \(|\psi , f\rangle _{o}\) displays fully super-Poissonian. Finally, from the results shown for Mandel’s parameter in Figs. 1 and 2, it can be seen that the non-classical depth and width of the ENCSS strongly influenced by the choice of the nonlinearity function.

Fig. 1
figure 1

Plots of the Mandel’s parameter \(Q_{i=1}\) corresponding with the states \(|\psi ,f\rangle _{e(o)}\), as function of \(|\alpha |=r\), with assuming some various types of the nonlinearity functions, (Solid and Black line) \(f(n)=1\), (Solid and Gray line) \(f_{\text {w}}\), (Dotted and Blue line) \(f_{\text {h}}\), (DotDashed and Green line)\(f_{\text {y}}\), (Dashed and Red line)\(f_{\text {v}}\), and (Dashing[large] and Orange line)\(f_{pa}\). The other coefficients are as \(k=2\), \(\frac{\chi }{\upsilon }=\lambda =0.5\) and \(|\eta |^2=0.8\)

Full size image
Fig. 2
figure 2

Plots of the Mandel’s parameter \(Q_{i=2}\) corresponding with the states \(|\psi ,f\rangle _{e}\)[left] and \(|\psi ,f\rangle _{o}\)[right] as function of \(|\alpha |=r\), with assuming some various types of the nonlinearity functions, (Solid and Black line) \(f(n)=1\), (Solid and Gray line) \(f_{\text {w}}\), (Dotted and Blue line) \(f_{\text {h}}\), (DotDashed and Green line)\(f_{\text {y}}\), (Dashed and Red line)\(f_{\text {v}}\), and (Dashing[large] and Orange line)\(f_{\text{pa}}\). The other coefficients are as \(k=2\), \(\frac{\chi }{\upsilon }=\lambda =0.5\) and \(|\eta |^2=0.8\)

Full size image

  • Quantum Polarization

The polarization degree of an electro-magnetics field of states is of considerable interest in various domains of quantum information theory [89,90,91,92]. For this purpose, quantum polarization has been studied as one of the criteria for non-classicality of quantum states [24, 36, 37, 42, 43]. Also, the relation between polarization squeezing and other non classical properties such as entanglement and quadrature squeezing was analyzed [93]. The quantum polarizations of the ENCSS are given by:

$$\begin{aligned} P^{|\psi , f\rangle _{e(o)}}=\frac{\sqrt{\langle s_{x}\rangle ^2+\langle s_{y}\rangle ^2+\langle s_{z}\rangle ^2}}{\langle s_{0}\rangle }, \end{aligned}$$
(7)

where \(s_{i}\) denotes the Stokes operators in terms of the annihilation and creation operators of first (second) mode of the field:

$$\begin{aligned} s_{x}&=a_{1}a^{\dag }_{2}+a^{\dag }_{1}a_{2}, \end{aligned}$$
(8a)
$$\begin{aligned} s_{y}&=i(a_{1}a^{\dag }_{2}-a^{\dag }_{1}a_{2}), \end{aligned}$$
(8b)
$$\begin{aligned} s_{z}&=a^{\dag }_{1}a_{1}-a^{\dag }_{2}a_{2}, \end{aligned}$$
(8c)
$$\begin{aligned} s_{0}&=a^{\dag }_{1}a_{1}+a^{\dag }_{2}a_{2}. \end{aligned}$$
(8d)

By considering \(\langle a^{\dag }_{2}\rangle =\langle a_{2}\rangle =0\), the polarization degree of the ENCSS recasts into:

$$\begin{aligned} P^{|\psi , f\rangle _{e(o)}}& =\frac{\sqrt{\langle s_{z}\rangle ^2}}{\langle s_{0}\rangle } \nonumber \\ & = \frac{\sqrt{\left( \langle N_{1}\rangle _{f, e(o)}-\langle N_{2}\rangle _{f, e(o)}\right) ^2}}{\langle N_{1}\rangle _{f, e(o)}+\langle N_{2}\rangle _{f, e(o)}}. \end{aligned}$$
(9)

It is clear that the maximum value of the polarization, i.e. \(P=1\) attached to a complete polarized state, while \(P=0\) refers to an unpolarized one. To study the effect of choosing different type of nonlinearity functions, we depicted the quantum polarization of the ENCSS versus \(|\alpha |=r\) for different values of the nonlinearity functions in Fig. 3. As Fig. 3a shows, variations of the polarization function are influenced, rigorously, by the choice of the first mode field of initial state. For example, by selecting the first mode field of state as the standard coherent state, the polarization function of the even-ENCSS starts from 0.45 and oscillates until it reaches its maximum value of 0.6, then it has a downward trend to reach a depolarized state, it then grows again to finally stabilize at 0.2. Although choosing the NLCS instead of the standard coherent state complicates the behavior of the polarization function, it improves the degree of polarization of the even-ENCSS up to 0.95. By selecting other nonlinearity functions instead of the photon-added one, we may prevent from depolarization of the even-ENCSS, then the polarization remains for a wide range of the field parameter \(|\alpha |\), and for large values of \(\alpha\), it stabilizes at 0.2. Figure 3 (b) shows that the polarization of the odd-ENCSS represents a same behavior; however, they start from unity, then decrease slowly by increasing the field parameter \(|\alpha |\), and finally tends to 0.2.

Fig. 3
figure 3

Polarization degree versus \(|\alpha |=r\) for both states \(|\psi , f\rangle _{e}\)[left] and \(|\psi , f\rangle _{o}\)[right], with assuming some various types of the nonlinearity functions, (Solid and Black line) \(f(n)=1\), (Solid and Gray line) \(f_{\text {w}}\), (Dotted and Blue line) \(f_{\text {h}}\), (DotDashed and Green line)\(f_{\text {y}}\), (Dashed and Red line)\(f_{\text {v}}\), and (Dashing[large] and Orange line)\(f_{pa}\). The other coefficients are as \(k=2\), \(\frac{\chi }{\upsilon }=\lambda =0.5\) and \(|\eta |^2=0.8\)

Full size image
Fig. 4
figure 4

Concurrence for both the even(odd)-ENCSS as function of \(|\alpha |=r\) with assuming some various types of the nonlinearity functions, (Solid and Black line) \(f(n)=1\), (Solid and Gray line) \(f_{\text {w}}\), (Dotted and Blue line) \(f_{\text {h}}\), (DotDashed and Green line)\(f_{\text {y}}\), (Dashed and Red line)\(f_{\text {v}}\), and (Dashing[large] and Orange line)\(f_{pa}\). The other coefficients are as \(k=2\), \(\frac{\chi }{\upsilon }=\lambda =0.5\) and \(|\eta |^2=0.8\)

Full size image

4 Entanglement analysis of the ENCSS

Because of great importance of entanglement as a highly complex phenomenon in quantum theory as well as the quantum information processing, here, we evaluate the entanglement degree of the ENCSS using the concurrence measure. Based on this criterion, a state \(\psi\) is entangled if it satisfies the inequality

$$\begin{aligned} 0\le C(\psi )\le 1, \end{aligned}$$
(10)

where a state with \(C(\psi )=0\) is separable, but \(C(\psi )=1\) denotes a maximally entangled state. Since these two-qubit-like entangled states are written as linear superposition of continuous variable and non-orthogonal basis; then to examine their entanglement, we rewrite them in terms of orthogonal bases. For this reason, we introduce the orthogonal bases \(|0\rangle _{1(2)}\), \(|1\rangle _{1(2)}\) of each subsystem 1(2) [24, 94] and corresponding with the even(odd)-ENCSS as follows

$$|0\rangle _{1} = |\alpha ,f\rangle ;\quad |1\rangle _{1} = \frac{{| - \alpha ,f\rangle - \mu |\alpha ,f\rangle }}{{\sqrt {1 - |\mu |^{2} } }},{\text{ }}$$
(11a)
$$|0\rangle _{{2,e(o)}} = | - \xi \rangle _{{e(o)}} ;\quad |1\rangle _{{2,e(o)}} = \frac{{|\xi \rangle _{{e(o)}} - \nu _{{e(o)}} | - \xi \rangle _{{e(o)}} }}{{\sqrt {1 - |\nu |^{2} } }},$$
(11b)

where we have:

$$\begin{aligned} \mu&=\langle \alpha ,f|-\alpha ,f\rangle \nonumber \\&=|\mathcal {N}_{f}|^2\sum ^{\infty }_{k=0} {(-1)^k\frac{r^{2k}}{k![f(k)!]^2}}, \end{aligned}$$
(12a)
$$\begin{aligned} \nu _{e}&=_{e}\langle -\xi |\xi \rangle _{e} \nonumber \\&=|\mathcal {N}_{e}|^2\sum ^{\infty }_{k'=0} {(-1)^{k'}\frac{r^{2k'}(2k')!}{k'!2^{2k'}}}, \end{aligned}$$
(12b)
$$\begin{aligned} \nu _{o}&=_{o}\langle -\xi |\xi \rangle _{o} \nonumber \\&=|\mathcal {N}_{o}|^2\sum ^{\infty }_{k'=0} {(-1)^{k'}\frac{r^{2k'}k'!2^{2k'}}{(2k'+1)!}} \end{aligned}$$
(12c)

Based on the above preliminaries, one can easily obtain \(|\psi , f\rangle _{e(o)}\) in the following form composed of the orthogonal bases \(|0\rangle _{1}\), \(|1\rangle _{1}\), \(|0\rangle _{2,e(o)}\), and \(|1\rangle _{2,e(o)}\):

$$\begin{aligned} |\psi , f\rangle _{e}&= A_{e}\left[ (\mu +\nu _{e})|0\rangle _{1}|0\rangle _{2,e} +\sqrt{1-|\nu _{e}|^2}|0\rangle _{1}|1\rangle _{2,e} +\sqrt{1-|\mu |^2}|1\rangle _{1}|0\rangle _{2,e}\right] , \end{aligned}$$
(13a)
$$\begin{aligned} |\psi , f\rangle _{o}&= A_{e}\left[ (\mu +\nu _{o})|0\rangle _{1}|0\rangle _{2,o} +\sqrt{1-|\nu _{o}|^2}|0\rangle _{1}|1\rangle _{2,o} +\sqrt{1-|\mu |^2}|1\rangle _{1}|0\rangle _{2,o}\right] , \end{aligned}$$
(13b)

and then the concurrence for the considered states will take the form

$$\begin{aligned} C^{|\psi , f\rangle _{e(o)}}=2|A_{e}|^2\sqrt{(1-|\mu |^2)(1-|\nu _{e(o)}|^2)} \end{aligned}$$
(14)

Figure 4 shows the variations of concurrence measure for both the even(odd) ENCSS as functions of \(|\alpha |=r\) for different types of the nonlinearity functions f. It is worthwhile to note that the concurrence of both the states \(|\psi , f\rangle _{e}\) and \(|\psi , f\rangle _{o}\) have similar behavior in which the entangled states exist in any region of \(|\alpha |=r\) for any types of f. It starts from zero, increases monotonically with r, and finally gets its maximum value \(C=1\) for all of the considered nonlinearity functions f, except for \(f_{h}\). It is worth noting that by selecting the field state of the first mode \(|\alpha ,f_{v}\rangle\), the maximum value of entanglement is maintained forever. However, the others are maximally entangled for a small range of \(2<r<7\), then descend with a negative slope and become separable. Therefore, selecting an appropriate nonlinearity function will not only increase the amount of entanglement of the ENCSS but also maintain entanglement.

5 Generation of ENCSS

In this section, we follow the method previously used by Karimi et al. [37] to generate the ENCSS. Based on the generalized Jaynes–Cummings model was previously used in Ref. [37], we extend this model to a nonlinear Jaynes-Cummings model in such a way that a \(\Lambda\)-type three-level atom interacts with two strong classical fields in the presence of two-mode quantized cavity field where the first mode field of cavity is an intensity dependent field in terms of nonlinear operators. Here, the cavity modes and classical fields are in resonant with the corresponding atomic transitions. Also, the two allowed transitions of the \(\Lambda\)-type three-level atom (\(|1\rangle\) \(\Leftrightarrow\) \(|3\rangle\)) are supposed to be a one-photon transition, and another transition (\(|2\rangle\) \(\Leftrightarrow\) \(|3\rangle\)) is a two-photon transition. The interaction Hamiltonian of the atom-field system can be expressed as:

$$\begin{aligned} H&= \underbrace{\Omega _{a}\left( \sigma _{13}e^{i\phi _{a}} +\sigma _{31}e^{-i\phi _{a}}\right) +\Omega _{b}\left( \sigma _{23}e^{i\phi _{b}} +\sigma _{32}e^{-i\phi _{b}}\right) }_{H_{Cl.}} \nonumber \\&\quad +\underbrace{g_{a}\left( \sigma _{13}A^{\dag }+\sigma _{31}A\right) +\Omega _{b}\left( \sigma _{23}{b^{\dag }}^{2}+\sigma _{32}b^{2}\right) }_{H_{Cav.}}, \end{aligned}$$
(15)

where \(\sigma _{ij}=|i\rangle \langle j|\) with \(i, j = 1, 2, 3\) are the atomic operators and \(A=f(n)a, A^{\dag }=a^{\dag }f(n)\) and \(b, b^{\dag }\) are the annihilation and creation operators of the mode a and b. We, also, consider the case of strong laser pulses, i.e., \(\Omega _{a},\Omega _{b}\gg g_{a},g_{b}\). Using the eigenvalue equations of the Hamiltonian \(H_{Cl.}\):

$$\begin{aligned}&H_{Cl.}|0\rangle =0, \end{aligned}$$
(16a)
$$\begin{aligned}&H_{Cl.}|\pm \rangle =\pm \sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}|\pm \rangle , \end{aligned}$$
(16b)

we introduce the atomic dressed basis as:

$$\begin{aligned}&|0\rangle =\frac{\Omega _{b}e^{-i\phi _{b}}|1\rangle -\Omega _{a}e^{-i\phi _{a}}|2\rangle }{\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}, \end{aligned}$$
(17a)
$$\begin{aligned}&|\pm \rangle =\frac{1}{\sqrt{2}} \left( |3\rangle \pm \frac{\Omega _{a}e^{i\phi _{a}}|1\rangle +\Omega _{b}e^{i\phi _{b}}|2\rangle }{\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\right) . \end{aligned}$$
(17b)

Then, one can rewrite the interaction terms \(H_{Cl.}\) and \(H_{Cav.}\) are given in Eqs. (11a, 11b) in terms of the above addressed basis as follows

$$\begin{aligned}&H^{'}_{Cl.}=\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}\sigma _{z}, \end{aligned}$$
(18a)
$$\begin{aligned}&H^{'}_{Ca.}=g_{a}f(n)a \nonumber \\&\quad \left[ \frac{\Omega _{a}e^{i\phi _{a}} \left( \sigma _{z}+\sigma _{-}-\sigma _{+}\right) }{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}} +\frac{\Omega _{b}e^{-i\phi _{b}}\left( |+\rangle \langle 0|+|-\rangle \langle 0|\right) }{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\right] \nonumber \\&\quad +g_{b}b^{2} \nonumber \\&\quad \left[ \frac{\Omega _{b}e^{i\phi _{b}}\left( \sigma _{z}+\sigma _{-} -\sigma _{+}\right) }{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}} -\frac{\Omega _{a}e^{-i\phi _{a}}\left( |+\rangle \langle 0|+|-\rangle \langle 0|\right) }{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\right] +h.c, \end{aligned}$$
(18b)

where we have defined \(\sigma _{z}:=|+\rangle \langle +|-|-\rangle \langle -|\), \(\sigma _{\pm }:=|\pm \rangle \langle \mp |\). To simplify the dynamics of the system, the total Hamiltonian of the system \(H^{'}=H^{'}_{Cl.}+H^{'}_{Ca.}\) in the interaction picture becomes:

$$\begin{aligned}H^{''} & =R^{\dag }H^{'}R-iR^{\dag }\frac{d R}{dt}\nonumber \\&=\frac{\left( \Omega _{a}e^{i\phi _{a}}g_{a}f(n)a+\Omega _{b}e^{i\phi _{b}}g_{b}b^{2}\right) \left[ \sigma _{z}+e^{-2it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}_{\sigma _{-}} -e^{2it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\sigma _{+}\right] }{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}+h.c. \end{aligned}$$
(19)

where we applied the transformation \(R=e^{-it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\left( |+\rangle \langle +|-|-\rangle \langle -|\right)\). In the strong laser regime, one can eliminate the rapidly oscillatory terms from Eq. (19) and obtain the effective interaction Hamiltonian as well as the corresponding time evolution operator in the standard picture as follows:

$$\begin{aligned} H_{eff.}&=\frac{\left( \Omega _{a}e^{i\phi _{a}}g_{a}f(n)a +\Omega _{b}e^{i\phi _{b}}g_{b}b^{2}+h.c\right) \sigma _{z}}{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}, \end{aligned}$$
(20a)
$$\begin{aligned} U&=Re^{-itH_{eff.}} \nonumber \\&=e^{-it\sigma _{z}\left[ \sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}} +\frac{g_{a}\Omega _{a}}{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}(e^{i\phi _{a}}f(n)a +e^{-i\phi _{a}}a^{\dag }f(n))+\frac{g_{b}\Omega _{b}}{2\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}(e^{i\phi _{b}}b^2+e^{-i\phi _{b}}{b^{\dag }}^2)\right] }. \end{aligned}$$
(20b)

Along with assuming the two-mode cavity field modes and the three-level atom initially prepared in the vacuum state \(|0\rangle _{a}|0\rangle _{b}\) and in the excited state \(|3\rangle\), respectively, also by making use of the time evolution operator in (20b) and setting \(\alpha :=-it\frac{g_{a}\Omega _{a}e^{-i\phi _{a}}}{\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\) and \(\xi :=-it\frac{g_{b}\Omega _{b}e^{-i\phi _{b}}}{\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}\), the state of the system after the passage of the atom through the cavity evolves to:

$$\begin{aligned} U|0\rangle _{a}|0\rangle _{b}|3\rangle & = \frac{e^{-it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}}{\sqrt{2}}e^{\alpha a^{\dag }f(n)-\alpha ^{*}f(n)a}e^{\frac{\xi }{2} {b^{\dag }}^2-\frac{\xi ^{*}}{2}b^2}|0\rangle _{a}|0\rangle _{b}|+\rangle \nonumber \\& \quad +\frac{e^{it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}}{\sqrt{2}}e^{-\alpha a^{\dag }f(n)+\alpha ^{*}f(n)a}e^{-\frac{\xi }{2} {b^{\dag }}^2+\frac{\xi ^{*}}{2}b^2}|0\rangle _{a}|0\rangle _{b}|-\rangle . \end{aligned}$$
(21)

By acting the appeared displacement and squeezing operators in Eq. (21) on the two-mode vacuum state, the evolved state can be reformed in the following form:

$$\begin{aligned} U|0\rangle _{a}|0\rangle _{b}|3\rangle & = \frac{e^{-it\sqrt{\Omega ^{2}_{a} +\Omega ^{2}_{b}}}}{\sqrt{2}}|\alpha ,f\rangle _{a}|-\xi \rangle _{e,b}| +\rangle \nonumber \\&\quad +\frac{e^{it\sqrt{\Omega ^{2}_{a}+\Omega ^{2}_{b}}}}{\sqrt{2}}| -\alpha ,f\rangle _{a}|\xi \rangle _{e,b}|-\rangle . \end{aligned}$$
(22)

It can be readily observed that by detecting the atom in the excited state \(|3\rangle\), the state of the system is collapsed to the state \(|\Psi ,f\rangle _{e}\) is given in Eq. (1a). Considering a same method, one can easily generate the introduced odd-ENCSS in Eq. (1b) by assuming the two-mode cavity field initially in the state \(|0\rangle _{a}|1\rangle _{b}\).

It is worth mentioning that, to derive an action of the nonlinearized displacement operator \(e^{\alpha a^{\dag }f(n)-\alpha ^{*}f(n)a}\) on the vacuum state \(|0\rangle _{a}\) in Eq. (21), we applied the universal disentangling formula [95], associated to the nonlinear algebra \([af(n),f(n)a^{\dag }]=f(n+1)-f(n)\) is given by

$$\begin{aligned}&e^{\alpha a^{\dag }f(n)-\alpha ^{*}f(n)a}|0\rangle \nonumber \\&\quad =\sum ^{\infty }_{n=0} {\left[ \sum ^{\infty }_{j=0}{\frac{n!}{(n+2j)!}\triangle _{n+1,j}(-|\alpha |^{2})^j}\right] \frac{\left( \alpha a^{\dag }\right) ^n}{n!}}|0\rangle . \end{aligned}$$
(23)

where we have

$$\begin{aligned}&\triangle _{n+1,0}=1, \end{aligned}$$
(24a)
$$\begin{aligned}&\triangle _{n+1,j}=\sum ^{n+1}_{k_{1}=1}{f(k_{1})}\sum ^{k_{1}+1}_{k_{2}=1} {f(k_{2})}...\sum ^{k_{j-1}+1}_{k_{j}=1}{f(k_{j})}. \end{aligned}$$
(24b)

For instance, corresponding to the para-Bose system with a nonlinearity function as \(f_{w}\), through inductive reasoning, on can derive

$$\begin{aligned}&\triangle _{2n+1,j}=\frac{(n+j)!(2n+2j+2\lambda -1)!(n+\lambda )!}{2^{j-1}j!n!(2n+2\lambda )!(n+j+\lambda -1)!}, \end{aligned}$$
(25a)
$$\begin{aligned}&\triangle _{2n+2,j}=\frac{(n+j)!(2n+2j+2\lambda +1)!(n+\lambda +1)!}{2^{j-1}j!n!(2n+2\lambda +2)!(n+j+\lambda )!}. \end{aligned}$$
(25b)

Thus, we have

$$\begin{aligned} |\alpha ,f_{w}\rangle&=e^{-\frac{|\alpha |^2}{2}}\sum _{n=0}^{\infty } \frac{\sqrt{2}\alpha ^{2n}}{\sqrt{(2n)!}!\sqrt{n!(\lambda +\frac{1}{2})_{n}}}_{1} \nonumber \\&\qquad F_{1}\left( -\lambda ,n+\frac{1}{2};\frac{|\alpha |^2}{2}\right) |2n\rangle \nonumber \\&\quad +e^{-\frac{|\alpha |^2}{2}}\sum _{n=0}^{\infty }\frac{\sqrt{2}\alpha ^{2n+1}}{\sqrt{(2n+1)!}!\sqrt{n!(\lambda +\frac{1}{2})_{n+1}}}_{1} \nonumber \\&\qquad F_{1}\left( -\lambda ,n+\frac{3}{2};\frac{|\alpha |^2}{2}\right) |2n+1\rangle , \end{aligned}$$
(26)

where the notations \((x)_{j}\) and \(_{1}F_{1}(a; b; x)\) stand for the Pochhammer symbol and the confluent hypergeometric function of the first kind, respectively. It is worth mentioning that, Lara et al. [88] already derived an action of the nonlinearized displacement operator on the vacuum state which leads to the NLCS \(|\alpha , f_{w}\rangle\) and their Nonclassical properties were well discussed.

6 Conclusion

Here, we introduced two-mode ENCSS, and studied their non-classical properties, such as the photon statistics, entanglement and quantum polarization for the famous nonlinearity functions \(f_{h}, f_{v}, f_{y}, f_{w}\). We showed that a selection of a nonlinearity function plays a key role in non-classical features of the introduced ENCSS. For example, we have studied photon statistics of the introduced states, and observed that all of the states include sub-Poissonian photon statistics in some ranges of the coherent amplitude \(|\alpha |\), except by selecting \(f_{w}\). However, by selecting the non-linearity functions \(f_{h}\) and \(f_{y}\), the photon statistics will be fully sub-Poissonian. Also, we have studied the quantum polarization and entanglement properties of the ENCSS, and showed that a proper selection of the nonlinearity function can prevent depolarization and disentanglement of these states. In particular, preparing the first mode of state in a NLCS, \(|\alpha ,f_{v}\rangle\), leads to a maximally two-mode ENCSS. Furthermore, all nonclassical features including sub(super)-Poissonian photon statistics, quantum polarization, and entanglement are exhibited simultaneously for some of the states under consideration which provides them as the capable states to be used as a physical resource in quantum information processing. To analyze, compare and match the quantum polarization with other non-classical features, one can observe that by choosing some values of the system parameters (see figure 3), the polarization degree of all two modes becomes zero and results an unpolarized situation, which is in accordance with the maximum amount of entanglement for these states. Finally, a theoretical scheme based on a nonlinear Jaynes–Cummings model was applied to generate these kind of states.