1 Introduction

Fig. 1
figure 1

The structure of an MPC with two spherical mirrors

Full size image

Multipass cells (MPCs) have been widely used in tunable diode laser absorption spectroscopy (TDLAS) to detect the concentration of trace gases [1,2,3,4,5,6,7,8,9]. Based on the Beer–Lambert law, the detection sensitivity by spectroscopy can be enhanced by increasing effective optical path lengths (OPLs). Various MPCs have been developed for this property, such as White cell [10,11,12], Herriott cell [13] and astigmatism MPC [14,15,16]. The White cell consists of three mirrors and has a relatively large volume, which limits its application in miniaturized instruments. The Herriott cell, composed of two identical spherical mirrors, is widely used due to its simplicity and good stability. However, the utilization of mirror surfaces is relatively low, as only one circle or ellipse pattern is formed on the mirrors. The astigmatism MPC can create Lissajous patterns and improve the utilization efficiency of mirrors. However, an astigmatic mirror is difficult to manufacture, and the cost is relatively high.

The two-spherical-mirror-based MPCs with dense patterns are widely applied to detect trace gas concentrations using the TDLAS technique [17,18,19,20,21], due to their superior characteristics of compactness, a long effective OPL, and affordable cost. In 2013, Krzempek et al. [17] achieved sub-ppb level ethane concentration measurements using an ultra-compact multipass gas absorption cell with five-concentric-cycle patterns. In 2015, Liu et al. [18] reported a scheme for the highly sensitive detection of methane by using a compact dense-pattern multipass cell with seven circular spot patterns. In 2019, Shao et al. [19] utilized a special Herriott-type multipass absorption cell with concentric-arc patterns to detect atmospheric CO and CH4 simultaneously. In 2020, Cui et al. [20] designed and fabricated a mini-MPC with a seven-nonintersecting-circle spot pattern to achieve ppb-level methane detection. In 2021, Wei et al. [21] detected atmospheric CH4 concentration by implementing a mini-multi-pass cell with the pattern of seven nonintersecting circles.

Over the years, researchers have reported ray-tracing methods and studied calculation models of densely patterned MPCs with two spherical mirrors [22,23,24,25,26]. A large number of MPC configurations can be obtained by numerous different combinations of parameters, including the curvature radius of mirrors, the distance between mirrors, the incident angles and the position of the incident point. The conventional theoretical method can only calculate patterns accurately but cannot search design parameters automatically [25]. Due to the lack of strategies for determining the optimal parameters, the MPC design process is usually very difficult and time-consuming. Furthermore, to achieve the re-entrant condition, parameters are usually modified manually [27], which relies on experience and cannot guarantee precision.

In this paper, we utilize the random walk (RW) and gradient descent (GD) algorithms to automate and optimize the MPC design process. The RW algorithm is applied for global exploration to determine the design parameters of the target MPC configuration with dense patterns. It significantly conserves computational power and calculation time compared to the traditional grid search method. The GD algorithm is performed for local exploitation to further optimize the re-entrant condition of MPCs in a fast and accurate way. A combination of the RW and GD algorithms is applied to optimize two types of optical MPC designs with dense patterns, which consist of two and four identical spherical mirrors. In addition, we utilize a clustering method to identify the desired patterns automatically according to their specific features. The simulation and experimental results show that the spot patterns formed on the mirrors are consistent with the theoretical calculations. The implementation of the RW and GD algorithms is effective and efficient for MPC optimization and can be carried out for more complex optical configurations.

2 Optimizing MPC design with two spherical mirrors

2.1 Modeling of two-spherical-mirror-based MPC

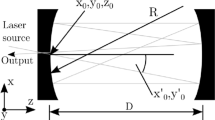
The structure of a two-spherical-mirror-based MPC is shown in Fig. 1. Two spherical mirrors with equal curvature radius R are separated by a distance d. An incident beam enters through the entrance hole with a diameter \({D}_{{\text{hole}}}\), reflects N times between the two mirrors, and forms dense patterns on each mirror surface before exiting through the same hole. The incident angles \(\theta\) and \(\phi\) can be written into the direction vector \(r^{(i)}\), where the subscript i denotes the ith reflection \((i=1,2,\ldots ,N)\). \(p_O^{(i)}\) and \(r_N^{(i)}\) are the coordinate values of the incident point and the normal vector of a point on a sphere, respectively. Because each reflective point and direction vector of the reflective beam can be considered as the incident point and the direction vector of the incident beam for the next reflection, the successive reflections between the mirrors follow iterative equations:

$$\begin{aligned}&\begin{aligned} t^{(i)}=&-r^{(i)} \cdot OC^{(i)}+\\&\sqrt{(r^{(i)} \cdot OC^{(i)})^2-OC^{(i)} \cdot OC^{(i)}+R^2}, \end{aligned} \end{aligned}$$
(1)
$$\begin{aligned}&P^{(i+1)}_O=P^{(i)}_O+t^{(i)}r^{(i)}, \end{aligned}$$
(2)
$$\begin{aligned}&r^{(i)}_N=(P^{(i+1)}_O-P_C^{(i)})/R, \end{aligned}$$
(3)
$$\begin{aligned}&r^{(i+1)}=r^{(i)}-(2r^{(i)} \cdot r^{(i)}_N)r^{(i)}_N, \end{aligned}$$
(4)
Fig. 2
figure 2

Four dense patterns selected and optimized by the combination of the RW and GD algorithms, where all patterns meet the re-entrant condition. a Sunflower-like petals, b four independent circles, c three inner petals with an outer circle of spots, and d two intersecting circles with an outer circle of spots

Full size image
Table 1 Parameters of the spot patterns depicted in Figs. 2a–d, including the y-coordinate and orientation angles \(\theta\) and \(\phi\) of the incident beam, the distance d between two mirrors, and number of reflections N under the re-entrant condition
Full size table

where \(OC^{(i)}=P^{(i)}_O-P^{(i)}_C\). Based on the modeling of the two-spherical-mirror-based MPC, a MATLAB software-based program was used to calculate ray tracing accurately. To simplify the calculations, we set the curvature radius R and the maximum reflection N to 100 mm and 300, respectively. The same spot patterns can be scaled up or down when the incident angles remain unchanged, and the curvature radius, mirror distance and incident position are multiplied by the same scaling factor simultaneously [23]. Considering the symmetry of the spherical mirrors, the x-coordinate value of the incident point is set to 0. Therefore, each set of design parameters contains four variables \((d, y, \theta , \phi )\). In addition, we set the minimum spot separation as 1 mm to avoid spot overlaps.

2.2 Global exploration to determine parameters by using RW algorithm

A variety of patterns are formed on mirror surfaces by changing the design parameters, including the curvature radius, the distance between mirrors, the position of the incident point and the incident angles. The traditional grid search method involves an exhaustive search through a defined parameter space. Using grid search to design MPCs is extremely slow and leads to a long execution time, as the search space contains all possible sets of parameters, providing numerous configurations [22]. The MPC design process can be greatly accelerated and improved by the usage of the RW algorithm, which has superiority in searching for the parameters of expected MPC designs automatically.

Fig. 3
figure 3

Four computed dense patterns selected by the clustering method: a two, b three, c four, and d five concentric circles. All patterns meet the re-entrant condition

Full size image

The RW algorithm encoded in MATLAB is applied for global exploration to determine the target MPC configurations. The walker, which represents a set of design parameters \((d, y, \theta , \phi )\), is generated randomly based on the following limitations: the distance between two mirrors is in the range of 0–200 mm; the y-coordinate value is within the boundary of the spherical mirrors; and the range of both incident angles \(\theta\) and \(\phi\) is 0–180\(^{\circ }\). We make the walker move K steps with a variable step size of \((\delta _d, \delta _y, \delta _{\theta }, \delta _{\phi })\). Here, \((\delta _d, \delta _y, \delta _{\theta }, \delta _{\phi })\) are independent variables, each having a Gaussian distribution [28] with a mean of 0 and different standard deviations \((\sigma _d, \sigma _y, \sigma _{\theta }, \sigma _{\phi })=(0.5, 0.5, 1, 1)\). For each movement, the parameters are updated within the limits above and follow the iterated process: \(d^{k+1}=d^{k}+\delta ^k_d\), \(y^{k+1}=y^{k}+\delta ^k_y\), \(\theta ^{k+1}=\theta ^{k}+\delta ^k_{\theta }\) and \(\phi ^{k+1}=\phi ^{k}+\delta ^k_{\phi }\) \((k=1,2,\ldots ,K)\). The requirements are predefined as follows: the distance between the incident spot and the final spot is smaller than \(D_{\text {hole}}\) = 3 mm, the number of reflections is larger than 100 and the OPL is longer than 10 m. The walker is stopped when the above design requirements are satisfied and the desired MPC is selected.

We generate M walkers and discard any walker that finds no target MPC after walking K steps. When M and K are set to 2000 and 100, respectively, approximately 1250 MPC configurations with dense patterns are found. Under the same boundaries of the design parameters and computational conditions, the average running time of the RW is approximately 2.9 h, while the traditional grid search method [22] takes   368.6 h. The RW method is almost 127 times faster than the traditional grid search method, resulting in efficient conservation of the calculation time and computational power. The above MPC configurations form many dense patterns, including sunflower-like petals, independent circles, a pattern of three inner petals with an outer circle of spots, and a pattern of two intersecting circles with an outer circle of spots, which are shown in Fig. 2.

Fig. 4
figure 4

Simulated patterns by using multi-ray tracing:  a two and b four concentric circles

Full size image

2.3 Local exploitation to optimize re-entrant condition by using GD algorithm

The GD algorithm is an efficient approach to optimize the re-entrant condition for the MPC configuration in a fully automated way. Starting from the initial set of design parameters calculated by the RW method, the GD algorithm exploits the optimal solution by updating the parameters in the negative gradient of the objective function. Under the re-entrant condition, the ray returns exactly to its incident point after N reflections and continues to retrace the same ray pattern again and again [27]. We define the distance between the Nth spot and the first spot as \(\varDelta _1\), which denotes the reentrancy of the incident point. The distance between the \((N+1\)th spot and the second spot is defined as \(\varDelta _2\), which represents the reentrancy of the incident direction.

To enable optimization toward the optimal result, the objective function is defined as \(J(d, y, \theta ,\phi )=\varDelta ^2_{1}(d,y,\theta ,\phi )+\varDelta ^2_{2}(d,y,\theta ,\phi )\) , and the optimization of the re-entrant condition is formulated as the minimization of the objective function. Here, \((d, y, \theta , \phi )\) are the design parameters. To demonstrate the process clearly, the design parameters are written in the form \(p_i(i=1,2,\ldots ,n)\). Minimizing \(J(p_i)\) with respect to the parameters by using the GD algorithm, the following iterative equations are obtained.

$$\begin{aligned} p_i^{(j+1)}=p_i^{j}-\eta (p_i) \cdot \frac{\partial }{\partial p_i^{j}}J^{j}(p_i^{j}). \end{aligned}$$
(5)

where j is the number of iterations and the learning rate \(\eta (p_i)\) determines the size of the steps we take to reach a minimum. \(\varDelta J^j\) is estimated by computing the difference between \(J^j\) and the last iteration \(J^{(j-1)}\), and the optimization process stops when \(\varDelta J^j\) is less than the given tolerance value \(\varepsilon\).

The process of automated optimization for the re-entrant condition of MPCs is presented by using the GD algorithm for local exploitation. To demonstrate the speed and accuracy of this approach, we apply it to optimize different patterns of MPC configurations with the initial parameters based on the calculated solutions of the RW method. The whole process takes only several minutes, and the magnitude of the deference \(\varDelta J\) for the last irritation is minimized below \(10^{-7}\). The spot patterns in Fig. 2 all meet the re-entrant conditions, which have been optimized automatically by performing the GD algorithm, and the corresponding parameters are listed in Table 1.

Fig. 5
figure 5

Two spot patterns observed on the mirror M2: a two and b four concentric circles

Full size image

2.4 Select target patterns by using clustering method

By varying the parameters, a large number of patterns can be obtained. Clustering analysis is an effective method for selecting the target patterns automatically according to the specific features, which can eliminate manual handling operations and reduce the computational cost efficiently. In this article, we focus on concentric-circle patterns, which have the following characteristics: (1) the spots pass through the concentric circles successively and are evenly distributed on each circle; (2) the center of the spots of each circle is near the center of the mirror.

Based on the results calculated by the RW algorithm, the clustering method is used to select the target patterns in an automated way. To analyze the concentric-circle patterns conveniently, we project the spots on the x–y plane and analyze the 2D coordinate value on mirror M2. The distance between the projected spot and the center of the mirror, that is, the radius r of the circle where it is located, is the criterion of classification. The steps for clustering are as follows.

Step 1: Initialization. We first determine the number of concentric circles m, choose the first m dots and calculate the radius \(r_n~(n=1,2,\ldots ,m)\) as the initial category set, where the subscript n denotes the spot located on the nth circle. Step 2: Classification. In this stage, spots are divided into m categories. We calculate the radius of each remaining spot and subtract \(r_n\) successively. The spot that has the minimum difference \(\vert \varDelta {\text {min}}_n\vert\) is placed in the nth category. To guarantee that the spots are accurately classified in relation to the circles to which they belong, \(\vert \varDelta {\text {min}}_n\vert\) should be smaller than the minimum spot interval limitation. Step 3: Update. The mean radius of each concentric circle is solved to update the category set \(r_n\). Step 4: Iteration. The second and third steps are repeated until the spot number in each circle remains unchanged. Step 5: Selection. The concentric-circle patterns are selected when the following criteria are met: the number of spots in each circle is equal, the difference between each \(r_n\) is larger than 0.5 mm to distinguish different circles, and the center of each circle is near the center of the mirror M2.

Fig. 6
figure 6

The structure of an MPC with four spherical mirrors; a 3D view and b top view

Full size image
Fig. 7
figure 7

Ellipse and Lissajous patterns of the four-spherical-mirror-based MPC. a, c Computed spot pattern on the mirror M1 and the red point represents the position of incident beam; b, d simulated results obtained by using TracePro and the black circle represents the entrance hole

Full size image

Based on the results of the clustering analysis, the representative patterns of two, three, four and five concentric circles are as shown in Fig. 3a–d. All corresponding parameters for the concentric-circle patterns are listed in Table 2, which have been optimized by the GD algorithm to satisfy the re-entrant condition. By extending chief-ray tracing to multi-ray tracing, we calculate both the position and the size of each spot, and optimize the quality of output beam. The incoming laser beam is simulated by multi rays, which are distributed evenly and placed on a circle outline. The diameter of incoming beam \(D_{\text {in}}\) is defined from 1 to 3 mm at the interval of 0.1 mm. The spots are deformed into ellipse shape due to the spherical aberration, and the ratio \(\beta\) is defined as the length of longer axis of ellipse to the diameter \(D_{\text {in}}\) [22, 26]. The quality of the output beam is optimized by adjusting the incoming beam to converge at one point \(P_f\) on the line \(P_O^{(1)}P_O^{(2)}\). Moreover, the above method is generalized for MPCs based on various configurations.

Table 2 Parameters of the spot patterns depicted in Fig. 3a–d, including the y-coordinate and orientation angles \(\theta\) and \(\phi\) of the incident beam, the distance d between two mirrors, and number of reflections N under the re-entrant condition
Full size table

It is worth noting that the size of spots depend on the diameter \(D_{\text {in}}\) and the point \(P_f\) on the line of chief ray. The deformation of spots is exhibited in Fig. 4a–b, which shows the output beam with optimal quality. MPCs with two and four concentric circles were built and tested experimentally, and the observed spot patterns are exhibited in Fig. 5a and b. The experimental results agree with the calculation simulations, which verifies the accuracy of the proposed approach. The ultra-compact MPCs with two and four concentric circle patterns achieve 49.77 m and 40.81 m OPL in the volume of 345.48 \({\text {cm}}^3\) and 279.48 \({\text {cm}}^3\), respectively, which have the great potential to develop more compact gas sensors and have a wide range of applications, such as respiratory diagnosis, industrial monitoring and safety inspection.

3 Optimizing MPC design with four spherical mirrors

The MPC with a long effective OPL in a small volume is considered as an important part of laser absorption spectroscopy due to its compactness and high sensitivity. These properties enhance the absorption spectroscopy signals and reduce the footprint of gas sensors. Huge amounts of MPC configurations can be obtained by varying design parameters, such as the curvature radius of mirrors, the distance between mirrors, the incident angles and the position of the incident point. Designing the desired MPC configuration becomes increasingly difficult and time-consuming when the dimension of the parameters grows. The RW algorithm is especially suitable for designing more complex configurations.

The configuration of an innovative MPC with four spherical mirrors is shown in Fig. 6. The two spherical mirrors in Fig. 1 are both cut in half, and the four mirrors are placed symmetrically along the z-axis with the rotation angle \(\alpha\). The incident beam enters the MPC through the entrance hole, reflects off M1, M2, M3 and M4 successively, and leaves through the same hole under the re-entrant condition. The ray tracing is simulated based on the recursion Eqs. (1)–(4). The design parameters contain six variables, including the rotation angle \(\alpha\), the distance d between two opposite mirrors M1 and M4 (or M2 and M3), the x and y values of the incident point, and the incident angles \(\theta\) and \(\phi\).

The combination of the RW and GD algorithms is applied to optimize the four-spherical MPC design in an automated way. When the distance between two opposite mirrors is 61.5 mm and \(\alpha\) is \(7.6^{\circ }\), independent ellipse patterns are formed, as shown in Fig. 7a. The OPL is 14.5 m after the 240 reflections of the laser. When the distance d and angle \(\alpha\) are adjusted to 70.8 mm and \(5.8^{\circ }\), respectively, the four-spherical-mirror-based MPC forms Lissajous patterns, which are similar to those of astigmatism MPCs. Figure 7c is a diagram of the calculated results for the MPC that includes 156 passes, leading to an effective OPL of 10.9 m. Figure 7b and d present the patterns simulated using TracePro, which agree well with the calculated results and illustrate the validity of the proposed approach.

The proposed method can be further developed to the optimize MPC configurations with more spherical mirrors. In addition, the algorithm can be extended to design MPCs with different curved mirrors, such as cylindrical mirrors and astigmatic mirrors. The combination of RW and GD algorithms is generalized to search parameters of various MPCs automatically and optimize the re-entrance condition intelligently.

4 Conclusions

In conclusion, we use the RW and GD algorithms to automate and optimize MPCs with dense patterns, which significantly reduces the computational power and calculation time required. The RW algorithm is generalized to select parameters of various MPCs automatically, and the GD algorithm is an effective method to optimize the re-entrant condition of MPCs. According to the specific features, the clustering method is used to identify target patterns; we focus on concentric-circle patterns in this paper. The ultra-compact MPCs with two and four concentric circle patterns achieve 49.77 m and 40.81 m OPL respectively, which is beneficial to the development of more compact and convenient gas sensors.

The proposed algorithms are tested in the optimization of two types of densely patterned MPC under the re-entrant condition. The two-spherical-mirror-based MPCs with two and four concentric circle patterns are built and designed, the observed patterns fit well with the theoretical calculations. The novel MPC with four spherical mirrors are designed and optimized based on the combination of RW and GD algorithms. The simulation and laboratory experiments show that the proposed approach is effective and efficient in optimizing the MPC automatically, which is promising for the design of more complex optical configurations and can open up the possibility to utilize optimization algorithms to guide parameter determination for MPC design.