Negative resonant modes in a hyperbolic metamaterial slot cavity

Abstract

We show that negative resonant modes with an inverse relationship between the wavelength and the cavity length can be excited in a hyperbolic metamaterial slot cavity (HMMSC) in addition to positive resonant modes. The observed negative resonant modes in an HMMSC are in sharp contrast to that observed in a metal slot cavity. We analyze the dynamics of the excited negative resonant modes in the visible spectrum regime as HMMSC parameters vary.

1 Introduction

Slot cavity resonators confine light in a nanoscale low-index material surrounded by high-index materials so that resonant modes with a very high field intensity can be excited [1]. In the beginning, slot cavity resonators have been realized using the index contrast between different dielectric materials [2]. Later, structures have been designed with thin dielectric layers between two metal slabs that support the excitation of surface plasmons, so that light can be confined in dimensions much smaller than the wavelength [3]. Therefore, the dimension of a metal slot cavity (MSC) can be significantly smaller than that of a dielectric slot cavity [3]. Additionally, the index of metal is much greater than that of dielectrics in optical regime, resulting in a significant enhancement of the confined light intensity within the dielectric material due to the continuity condition of the normal component of displacement vector at each metal–dielectric interface.

Very high index contrast can also be created between a hyperbolic metamaterial (HMM) and a dielectric so that the confined light intensity can be significantly increased in an HMM slot cavity (HMMSC) [4]. HMMs are artificial materials that are realized by alternating dielectric layers. In the visible spectrum regime, HMMs are designed with a metal in one of the alternating layers. The optical properties of HMMs can be greatly engineered as the indices are different and have opposite signs along in-plane ($\varepsilon _\bot$) and perpendicular-plane ($\varepsilon _\parallel$) directions so that the constant frequency surface becomes hyperbolic for 2D and hyperboloid for 3D analysis. The opposite signs of $\varepsilon _\perp$ and $\varepsilon _\parallel$ create two possible hyperbolic regimes: (1) $\varepsilon _\perp <0$ and $\varepsilon _\parallel >0$ make the medium positively refractive and (2) $\varepsilon _\parallel <0$ and $\varepsilon _\perp >0$ make the medium negatively refractive [5]. The first case can produce zeroth-order resonator due to the negative-phase accumulation by a traveling wave inside a cavity with dimension $\sim \lambda _0/20$, where $\lambda _0$ is the wavelength of the incident light [6]. In this work, we are particularly interested in the second case with the incident light in the visible spectrum.

Recently, Travkin et al. presented a hyperbolic metamaterial structure to control dispersion in a near-infrared subwavelength resonator [7]. They designed a hyperbolic metamaterial terminated by metal layers at two ends. Therefore, a vertical cavity is created between two metal layers, and this cavity can support Fabry–Pérot modes due to reflections from the two metal layers. Travkin et al. obtained a fixed dispersion relation for the zeroth-order mode and a degenerative behavior for the first-order mode.

In this work, we report the excitation of negative resonant modes in an HMMSC in the visible wavelength range. The wavelengths of the zeroth- and first-order resonant modes have an anomalous negative correlation with the length of the designed HMMSC. We show that the modes propagating along the anisotropy axis can be exploited as resonant modes and the resonances of these modes depend mainly on the dimensions of the cavity.

2 Theoretical modeling

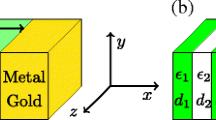
In Fig. 1a, we show a schematic illustration of the HMMSC that we have designed and analyzed in this work. In the designed HMMSC, germanium (Ge) and silver (Ag) layers are periodically interleaved in the y-direction with a periodicity $d = 10$ nm. We use effective medium theory to calculate the longitudinal ($\varepsilon _\perp = \varepsilon _x = \varepsilon _z$) and transverse ($\varepsilon _\parallel = \varepsilon _y$) dielectric constants of the designed HMMSC as [8]:

$$\begin{aligned} \begin{aligned} \left. \begin{array}{l} {\varepsilon _x} = {\varepsilon _z} = {f_m}{\varepsilon _m} + \left( {1 - {f_m}} \right) {\varepsilon _d}\\ {\varepsilon _y} = {\left[ {\frac{{{f_m}}}{{{\varepsilon _m}}} + \frac{{1 - {f_m}}}{{{\varepsilon _d}}}} \right] ^{ - 1}} \end{array} \right\} , \end{aligned} \end{aligned}$$

(1)

where $f_m$ is the metal fraction in HMM, and $\varepsilon _m$ and $\varepsilon _d$ are the dielectric constants of metal and dielectric, respectively. Since visible spectrum encompasses most of the vibrational and electronic resonances of a material, we set $f_m = 0.5$ so that the negative refractive index region of the HMM overlaps with the visible spectrum.

To simulate the interactions of the incident light with the designed HMMSC, we solve Maxwell’s equations using a full-field finite difference time domain (FDTD) technique. We assume that a transverse-magnetic polarized light is incident normally on the designed HMMSC in the x-direction. We vary the wavelength of the incident light from 300 to 800 nm and consider the materials dispersive, i.e., their optical properties vary with the light wavelength. The wavelength-dependent optical properties of Ge and Ag are taken from Ref. [9]. We have modeled Ge as a dielectric without loss and Ag as a lossy metal. While modeling Ag, we considered six resonances at 0, 1.52, 61.1, 136.6, 151.6, and 277 $\mu$m with oscillator strengths 0.845, 0.065, 5.646, 0.840, 0.011, and 0.124, respectively. The damping of the resonances in our simulations is 0.048, 3.886, 2.419, 0.916, 0.065, and 0.452 in unit of e/ℏ. Although Ge would be absorptive in practice, we believe that the difference in results would be merely quantitative.

In this work, FDTD simulations are performed using the commercial software Lumerical [10], while the effective medium theory and transfer matrix method are solved using home-written codes. The post-processing and data analysis of FDTD simulation results are also performed using home-written codes. In FDTD simulations, the mesh grids are automatically generated by the software based on local refractive indices and thicknesses of the materials. The convergence of time step is adjusted by the software. We monitored the conservation of total energy in the computational domain and ensured the absence of any instability during FDTD simulations.

Fig. 1

a Schematic illustration of HMMSC. Normalized electric field profiles of resonant modes at 525 nm in b HMMSC and c Ag slot cavity. d Cut-through of the electric field profiles in (b) and (c) along the vertical solid and dashed lines, respectively. We assume $w = 90$ nm, $g = 5$ nm, $t = 90$ nm, and the host material is air. For simulation purposes, each corner of the cavity has been rounded by 2 nm

3 Results

In Fig. 1b–d, we analyze the interactions of the incident light with slot cavities that are formed from HMM–dielectric–HMM and metal–dielectric–metal structures. The dielectric constant of HMM is calculated using the effective medium theory. In Fig. 1b, the incident light couples significantly to both the dielectric slot and the HMMs. By contrast, in Fig. 1c, the incident light couples only to the dielectric slot and decays sharply away from the metal-dielectric interface. In Fig. 1d, we find that the electric field of the confined light enhances more in the HMMSC slot cavity than in the MSC.

Fig. 2

a Scattering cross section ($\sigma$) for three different t when $w = 90$ nm and $g = 5$ nm. b $\sigma$ for three different g when $w = 90$ nm and $t = 90$ nm

In Fig. 2, we investigate the scattering cross section ($\sigma$) of the designed HMMSC at different wavelengths when the thickness (t) of the HMM and the gap (g) between HMMs vary. Here, the layered HMMs are solved using FDTD technique to determine resonances and sensitivities of resonances with dimensional parameters. In Fig. 2a, with $t=90$ nm, we note three distinct peaks for $\sigma$. The first peak at $\sim$ 352 nm is due to the excitation of the Fabry–Pérot cavity mode within the dielectric slot. The peaks at $\sim$ 525 nm and $\sim$ 632 nm are due to the excitation of resonant modes in HMMs. The resonant mode at $\sim$ 525 nm is in the hyperbolic regime, i.e., HMMs have $\varepsilon _y<0$ and $\varepsilon _x>0$ at this wavelength, and therefore, the excited mode is a negative mode [5]. The hyperbolic constant frequency surface $\omega (\overrightarrow{k})$ is shown in Fig. 3. Negative refraction occurs when $\overrightarrow{S} \cdot \overrightarrow{k} < 0$, where $\overrightarrow{S}$ and $\overrightarrow{k}$ are the Poynting vector and the wavevector, respectively. The index of the resonant modes has been solved using the approach described in “Appendix”. We note that the resonant mode at $\sim$ 632 nm is a positive index mode as both $\varepsilon _x>0$ and $\varepsilon _y>0$ at this wavelength.

In Fig. 2a, the excited modes in HMMs resonate with decreased strengths and shorter resonant wavelengths as t decreases to 60 nm from 90 nm. As t decreases further to 40 nm, the negative resonant mode no longer exists, as the anomalous mode cannot resonate with such a small t. These negative modes are in sharp contrast to the negative modes in an MSC as have been reported earlier [11]. Negative modes in an MSC arise since more field resides in metal than in dielectric, and the direction of Poynting vector in metal is opposite to that in dielectric due to the negative dielectric constant of metal. Hence, these modes have anti-parallel phase and group velocity, which yield negative mode index in an MSC [12]. However, in our designed HMMSC, the negative modes result from the material properties of HMM. We note that the phase and group velocity of the coupled light to our designed HMMSC are at an obtuse angle, and they are not necessarily anti-parallel in direction.

We show that resonant modes can be excited in an HMMSC in the y-direction—which is not the case for an MSC [13]. If g increases, the interaction between HMMs decreases, which results a blue shift in the resonance as shown in Fig. 2b. By contrast, as g decreases, the excited modes in HMMs interact and two spectrally separated modes are created. We note that the resonance at $\sim$ 352 nm remains unchanged as g changes since this mode is the Fabry–Pérot cavity mode. If $g\ll 5$ nm, the solutions of Maxwell’s equations may lead to a non-physical divergence of the field intensity. At such a small length-scale, quantum tunneling becomes important, hence a complete density functional analysis is required [14]. Therefore, we have limited our study to $g\gtrsim 5$ nm so that Maxwell’s equations describe the dynamics of the system with high accuracy.

Fig. 3

a Schematic illustration of constant frequency surface of hyperbolic media (for $\varepsilon _x>0$ and $\varepsilon _y<0$). The coordinates read as $A\equiv (\tilde{k}_x, \tilde{k}_y)$, $B\equiv (-\tilde{k}_x, \tilde{k}_y)$, $C\equiv (-\tilde{k}_x, -\tilde{k}_y)$, and $D\equiv (\tilde{k}_x, -\tilde{k}_y)$ with $\tilde{k}_x = \sqrt{(1-\epsilon _h/\epsilon _y)/(1/\epsilon _x - 1/\epsilon _y)}$ and $\tilde{k}_y = \sqrt{(\epsilon _h/\epsilon _x-1)/(1/\epsilon _x - 1/\epsilon _y)}$, where $\epsilon _h$ is the dielectric constant of the homogeneous medium (the dashed circle); $\epsilon _{x,y}$ are the dielectric constants along x and y axes, respectively, of the hyperbolic medium. Here, light is negatively refracted as is shown by the transmitted pointing vector $S_t$. b Schematic illustration of negative refraction in HMM for $\varepsilon _x>0, \varepsilon _y<0$

The relation between the width of the cavity w and the resonance wavelength $\lambda _0$ is given by:

$$\begin{aligned} w = \left( m \pi -\phi \right) \frac{\lambda _0}{2\pi } \frac{1}{n_{\mathrm {eff}}}, \end{aligned}$$

(2)

where m is the order of resonance, $\phi$ is the accumulated phase in a single round-trip propagation, and $n_{\mathrm {eff}}$ is the mode index of slot cavity. In Fig. 4a, we show the resonance peaks of the excited modes of Fig. 2a as a function of the cavity width (w). We find an anomalous trend for the two modes that are excited at shorter wavelengths. These two modes exhibit an inverse relationship with the cavity width in contrast to that found in a Fabry–Pérot cavity [13]. The resonance wavelength decreases since these modes exist in the hyperbolic regime where $\varepsilon _x>0$ and $\varepsilon _y<0$, and the refractive index is negative, as shown in the shaded region of Fig. 4b. This behavior is evident from Eq. (2) as $\mathrm {Re}[n_{\mathrm {eff}}]<0$ leads to a negative slope in $\lambda _0$ vs. w relationship when $\phi$ is positive. The positive sign of $\phi$ is confirmed from the direction of $k_t$ in Fig. 3a, since the y components of both $k_t$ and $k_0$ have the same sign.

Fig. 4

a Linear fit for the dynamic shift of resonance peaks of $\sigma$ in Fig. 2. The $\bullet$ and $+$ symbols denote negative modes as the resonance is blue-shifted with longer resonator. The positive mode is denoted by $\diamondsuit$. b The real parts of $\varepsilon _x$ and $\varepsilon _y$ of HMM. The hyperbolic region is shaded green. In the non-shaded region, the waveguide is elliptical since $\varepsilon _x$ and $\varepsilon _y$ have the same sign

We note that the transfer matrix and the FDTD calculations are performed assuming normally incident light in this work. For oblique incidence, we expect a quantitative shift of the resonance features for the designed HMMSC, however, without any qualitative change in the resonance spectrum. Therefore, the results obtained with the normally incident light will remain valid for a more general case.

4 Conclusion

In conclusion, we have investigated the negative index regime of HMM for applications in a slot cavity. We find that the propagating modes along the anisotropy axis can be exploited as resonant modes and the modes that fall within the hyperbolic regime show an inverse relation with the width of the cavity. The HMMSC with multiple resonant wavelengths in visible spectrum has promising applications in Raman sensing, enhanced light-matter interaction for laser cavity, and in cavity optomechanics.

Appendix

We derive the dispersion relation by calculating the transfer matrix for each of the interfaces of the layered HMMs. Transfer matrix for a dielectric–HMM interface is given by:

$$\begin{aligned} \begin{array}{l} {\mathrm {M} _{\mathrm{H},\mathrm{d}}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{\mathrm{M} _{11} }} & {} {{\mathrm{M} _{12} }}\\ {{\mathrm{M} _{21} }} & {} {{\mathrm{M} _{22}}} \end{array}} \right] ,\\ \\ {\mathrm {M} _{11}} = \frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }} - i\frac{{{\varepsilon} _{y} {k} _{y} }}{{{\varepsilon} _{x} {\kappa} _{d} }}, {\mathrm{M} _{11} = \mathrm{M} _{22}} ,\\ {\mathrm{M} _{12}} = \frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }} + i\frac{{{\varepsilon} _{y} {k} _{y} }}{{{\varepsilon} _{x} {\kappa} _{d} }}, {\mathrm{M} _{12} = \mathrm{M} _{21}} , \end{array} \end{aligned}$$

(3)

and for HMM–dielectric interface is given by

$$\begin{aligned} \begin{array}{l} { \mathrm{N} _{\mathrm{d},\mathrm{H}}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{ \mathrm{N} _{11} }} & {}{{ \mathrm{N} _{12} }}\\ {{ \mathrm{N} _{21} }} & {}{{ \mathrm{N} _{22} }} \end{array}} \right] ,\\ \\ { \mathrm {N} _{11}} = {\left( {\frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }}} \right) } ^{ - 1} + {i}\frac{{{\varepsilon} _{x} {\kappa} _{d} }}{{{\varepsilon} _{y} {k} _{y} }}, { \mathrm{N} _{11} = \mathrm{N} _{22} },\\ { \mathrm{N} _{12}} = {\left( {\frac{{{k} _{x}^{2} }}{{{k}_{0}^{2}}} + \frac{{{\varepsilon} _{y} {k} _{y}^{2} }}{{{\varepsilon} _{x} {k} _{0}^{2} }}} \right) } ^{ - 1} - {i}\frac{{{\varepsilon} _{x} {\kappa} _{d} }}{{{\varepsilon} _{y} {k} _{y} }}, { \mathrm{N} _{12} = \mathrm{N} _{21} }. \end{array} \end{aligned}$$

(4)

In Eqs. (3) and (4), ${k}_{y}$ is the y-component of wavevector inside HMM and ${\kappa} _{d}$ is the wavevector inside dielectric host, which are related by equations

$$\begin{aligned} \begin{array}{l} {\kappa} _{d} = \sqrt{{k} _{x}^{2} - {\varepsilon }_{dh} {k} _{0}^{2} } ,\\ \frac{{{k} _{x}^{2} }}{{{\varepsilon} _{y} }} + \frac{{{k} _{y}^{2} }}{{{\varepsilon} _{x} }} = {k} _{0}^{2} , \end{array} \end{aligned}$$

(5)

where ${\varepsilon }_{dh}$ is the dielectric constant of host matrix. Transfer matrices for propagation through an HMM and dielectric of lengths t and g, respectively, become

$$\begin{aligned} \begin{array}{l} {\mathrm {D} _\mathrm {H}} = \left[ {\begin{array}{*{20}{c}} {{e} ^{ - i{k} _{y} t} } & {}0\\ 0 & {}{{e} ^{i{k} _{y} t} } \end{array}} \right] ,~~~ {\mathrm {D} _\mathrm {d}} = \left[ {\begin{array}{*{20}{c}} {{e} ^{{\kappa} _{d} g} } & {}0\\ 0 & {}{{e} ^{ { - \kappa } _{d} g} } \end{array}} \right] . \end{array} \end{aligned}$$

(6)

Thus the overall transfer matrix for the HMM slot cavity shown in Fig. 1a is

$$\begin{aligned} \begin{array}{l} \mathrm {S }= \left[ {\begin{array}{*{20}{c}} {{\mathrm{S} _{11}} } & {}{{\mathrm{S} _{12} }}\\ {{\mathrm{S} _{21}} } & {}{{\mathrm{S} _{22} }} \end{array}} \right] ,\\ \quad = {\mathrm{N} _{\mathrm{d},\mathrm{H}} \mathrm{D} _\mathrm{H} \mathrm{M} _{\mathrm{H},\mathrm{d}} \mathrm{D} _\mathrm{d} \mathrm{N} _{\mathrm{d},\mathrm{H}} \mathrm{D} _\mathrm{H} \mathrm{M} _{\mathrm{H},\mathrm{d}}}. \end{array} \end{aligned}$$

(7)

The quantities M, N, and D are found from Eqs. (3), (4), and (6), respectively. Now, applying the boundary condition [13]

$$\begin{aligned} {\mathrm {S}_{11} = 0}, \end{aligned}$$

(8)

and solving for ${k}_{x}$ and ${k}_{y}$, the mode index is determined for particular set of parameter values, i.e., g, ${\varepsilon} _{x}$, ${\varepsilon} _{y}$, and ${\varepsilon} _{dh}$ at a desired wavelength.