Structuring a laser beam subject to optical Kerr effect for improving its focusing properties

Abstract

The use of laser beams made up of ultrafast pulses for the processing of materials can be bothered by the consequences of optical Kerr effect (OKE) cumulated by the propagation through optical devices (windows, laser crystal, prisms, lenses, …). The latter are mainly a reduction of the intensity in the focal plane accompanied by a distortion of the temporal and spatial pulse shape. We present a comparative study on such distortions for Gaussian, super-Gaussian and LG₁₀ (one central peak surrounded by a ring) beams. It is demonstrated that the LG₁₀ beam shows sensitivity to OKE which is smaller than that of the Gaussian LG₀₀, and super-Gaussian beams. As a result, the focusing performances of the LG₁₀ beam are quite superior to that observed with Gaussian or super-Gaussian beam: a higher on-axis intensity, a narrower intensity pattern, and a temporal shape and an energy fluence almost undistorted.

1 Introduction

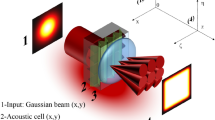
Innovations in applications of ultrafast lasers in materials processing has undergone a rapid development in the last few years. This is mainly due to the remarkable properties of ultrafast lasers output which is made up of pulses having a short duration in the femtosecond range, and possible high peak powers. In this case, the irradiated materials can be evaporated very quickly before any thermal effects could be induced. This is particularly relevant for laser material processing of small parts as 3D photonics crystals [1], micromachining on micro- or nanoscales [2,3,4], optical data storage [5], lab-on-a-chip photonics devices [6], and integrated photonics [7]. All these, and many other applications are based on the focusing of ultrashort pulses, and the focusing quality is of primary importance for the success of femtosecond laser processing technology. The wording “focusing quality” refers to the size of the focal spot and its intensity: ideally the first (second) has to be small (high). Among the possible phenomena that could reduce the “focusing quality”, let us look more closely to the Optical Kerr effect (OKE) which is a phenomenon playing an important role in the spatial and temporal degradation of the focal spot. The propagation of a high intensity laser beam in a Kerr medium is a very old subject started very early by considering the question of filamentation and beam breakup [8, 9]. In this paper, we will not consider these aspects of nonlinear propagation but we will be interested in the focusing of a laser beam having undergone OKE by passing through various optical devices (windows, amplifying crystals, prisms, lenses, …). More precisely, we will focus on the possibility of reducing the spatiotemporal distortion of the focal spot, due to OKE, by structuring spatially the laser beam to be focused. For sake of simplicity, we will consider the setup shown in Fig. 1 where the Kerr medium set against the focusing lens symbolises the OKE cumulated by the high intensity laser beam when crossing the various optical components which are present in the laser system, including the final focusing lens. The Kerr medium in Fig. 1 introduces a nonlinear phase shift $\Delta \varphi (\rho ,t)$, where $\rho$ is the radial coordinate and t the time, which has to be considered as an aberrated lensing effect.

Fig. 1

Set-up showing the geometry of the diffraction of a collimated Gaussian beam subject to optical Kerr effect (OKE) characterised by a Kerr phase shift $\Delta \varphi (\rho ,t)$

It is worthwhile to recall that the usual Gaussian beam subject to OKE shows at least two features when focused:

• 1. Since the Kerr effect can be view as a lensing effect, it results a longitudinal shift of the best focus position, as illustrated in Fig. 1, which leads to a reduction of the intensity in the focal plane.

• 2. In addition to the above focus shifting, one observes that the aberrations due to OKE distort the intensity beam profile in the focal plane which is no longer Gaussian in shape but is made up of a central peak surrounded by rings whose number is increasing with intensity.

It is important to note that taking OKE into account is not only necessary in large laser systems but also in a relatively smaller one as long as we are dealing with short pulses in the femtosecond range. A simple example will illustrate this: recently, it has been reported that the crossing of a 4-cm fused-silica sample by a laser pulse having a width W = 1 mm, a duration 700 fs and an energy equal to 220 µJ induces an OKE characterised by a nonlinear on-axis phase shift of $2\pi$ [10]. It will be shown later that such on-axis phase shift has several consequences to the focusing quality detriment. The spatiotemporal distortion of the focal intensity profile is difficult to be highlighted using a classical sensor such as CCD camera because of the stacking phenomenon which superposes the fast time evolution of distorted intensity profile, thus blurring the phenomena which are theoretically studied in this paper. Note that the right instrument for observing the spatiotemporal distortion of ultrashort pulses should be a streak camera which is a very expensive measurement device.

In Sect. 2, we will revisit the spatiotemporal distortions suffered by a focused Gaussian beam subject to OKE. It is important to note that relatively recently these distortions can be reduced using a technique [11] known as Simultaneous spatial and temporal focusing (SSTF). This technique, comparable to the CPA technique (chirped pulse amplification), involves the use of a pair of gratings having the role to disperse laterally the frequencies present in the incident short pulse. These frequencies are recombined by a focusing lens, and the various spectral components overlap. As a result, the shortest pulse duration together with the highest intensity are reached in the geometric focus of the focusing lens. We can note another recent technique known as dual-beam technique [12] having the capacity to mitigate the consequences of OKE. For our part, we wish to propose in Sect. 2 a new method for reducing the spatiotemporal distortion due to OKE. In this method, we show that the use of a LG₁₀ beam instead of the usual LG₀₀ (Gaussian) is beneficial for maintaining a high level of intensity for the focused beam subject to OKE. It is seen that using the LG₁₀ instead the LG₀₀ beam allows to strongly reduce the detrimental focal zoom phenomenon. In Sect. 3, we will examine the Kerr lensing effect associated to a super-Gaussian beam which has the reputation to be able to reduce the detrimental consequences of self-focusing.

2 Focusing a pulsed LG₀₀ and LG₁₀ beams subject to OKE

The focusing properties of a laser beam subject to optical Kerr effect (OKE) is a challenging subject matter having a great importance since it leads usually to a deterioration of the focusing performance. The latter can be summarised through the size of the focal spot and its intensity. Before getting to the hearth of the matter, it is worth noting to recall some basic elements about the OKE in a nonlinear medium. The latter can be the amplifying medium or any transparent optical element (lenses, glass plate, prism, …). The refractive index $n(\rho )$ of the nonlinear medium varies with the intensity $I(\rho )$ of the laser beam travelling down, and is written as follows

$$n(\rho ) = n_{1} + n_{2} \cdot I(\rho ),$$

(1)

where n₂ (n₁) is the nonlinear (linear) refractive index, and $\rho$ is the radial coordinate. The incident laser beam under consideration is the usual collimated Gaussian beam having an intensity profile $I(\rho )$ described by the following equation:

$$I(\rho ) = I_{0} \exp \left[ { - 2\rho^{2} /W^{2} } \right],$$

(2)

where $I_{0}$ is the on-axis intensity, and W = 1 mm the beam width. As a result, the incident beam is subject to a Kerr phase shift $\Delta \varphi (\rho )$ given by

$$\Delta \varphi (\rho ) = kn_{2} dI(\rho ),$$

(3)

where d is the Kerr thin medium thickness, and k = 2π/λ, with λ = 1064 nm the wavelength. Note that we have omitted in Eq. (3) the term $kn_{1}^{{}} d$ since it does not carry any aberration, and consequently does not contribute to the Kerr lensing effect. By taking into account the relationship, for the Gaussian beam, between its power P and on-axis intensity, namely $I_{0} = 2P/(\pi W^{2} )$, the Kerr phase shift is written as follows:

$$\Delta \varphi (\rho ) = \varphi_{0} \exp \left[ { - 2\rho^{2} /W^{2} } \right],$$

(4)

with $\varphi_{0} = \frac{{4n_{2} Pd}}{{\lambda W^{2} }}.$

In fact, Eq. (4) represents a phase aberration containing from one side a defocus term and high-order spherical aberrations as shown in [13], and summarised in Appendix. As a result, the phase shift $\Delta \varphi (\rho )$ is responsible to a Kerr lensing effect leading to a longitudinal shift of the best focus position toward the lens of focal length $f_{L} = 125\;{\text{mm}}$ as depicted in Fig. 1. The first consequence of this focus shifting is a reduction of the intensity in the focal plane $z = f_{L}$, and consequently a widening of the focal spot. In practice, Kerr lens are generated by OKE at high level of power in most cases which can only observed with short pulses. Since in this case $\varphi_{0}$ is necessarily time-dependent, it results that the position z_max of the best focus will change with time. This phenomenon gives rise to the so-called “focal zoom” which is well described in [14]. Such focal spot radius changes have been experimentally recorded using a streak camera [15, 16]. In addition to this focal zoom phenomenon, a supplementary widening of the spot in the reference plane $z = f_{L}$ could be occur due to the spherical aberration contained in $\Delta \varphi (\rho )$. Consequently, the Kerr lensing effect induced by laser pulses is responsible of spatio-temporal phenomena leading to a distortion of the temporal and spatial profiles. The objective of this paper is to demonstrate that the deformation of the temporal shape of the focused pulse as well as the phenomenon “focal zoom” observed with a Gaussian LG₀₀ beam can be strongly reduced using a LG₁₀ beam instead the usual LG₀₀ beam. It is important to note that the above time-dependent distortion mechanism is not observable only for large fusion laser system, but is expected to play a role for smaller laser systems. The latter are able to deliver high power pulses in the TW range thanks to the CPA technique (chirped pulse amplification). In addition, the impact of OKE occurring inside the focusing lens upon the field pattern in the plane $z = f_{L}$ has been reported for high-intensity Hermite–Gauss or Laguerre–Gauss beams [17].

The incident beam subject to OKE and focused by the lens of focal length $f_{L}$ is characterised by the diffracted intensity $I_{d} (r,z,t) = \left| {E_{d} (r,z,t)} \right|^{2}$, where $E_{d} (r,z,t)$ is given by the well known Fresnel–Kirchhoff integral

$$E_{d} (r,z,t) = \frac{2\pi }{{\lambda z}}\int\limits_{0}^{\infty } {E_{in} (\rho )\exp [ - i\Delta \varphi (\rho ,t)]} \exp \left[ {\frac{{i\pi \rho^{2} }}{\lambda }\left( {\frac{1}{{f_{L} }} - \frac{1}{z}} \right)} \right]J_{0} \left[ {\frac{2\pi }{{\lambda L}}r \cdot \rho } \right]\rho d\rho ,$$

(5)

where r ($\rho$) is the radial coordinate in plane z (lens plane), $J_{0}$ is the zero-order Bessel function of first order, $\lambda = 1064\;{\text{nm}}$ is the light wavelength. The integral given by Eq. (5) is calculated numerically using a FORTRAN routine based on the numerical integrator dqdag from the International Mathematics and Statistical Library (IMSL). In the next, all the transverse and longitudinal intensity distributions are given in arbitrary unit but remain comparable. It is important to note that the diffraction integral given in Eq. (5) is based on the assumption that the incident beam is monochromatic. We can then wonder about its validity for an ultrashort pulse having consequently a finite spectrum. This point is discussed in Appendix, and the conclusion is that Eq. (5) can be used if the pulse duration $\tau$ is not too small. In the following, we will assume that this condition is fulfilled.

To take into account the time dependence of the incident beam power, we will assume a Gaussian dependence with time. The incident collimated beam is either a LG₀₀ or LG₁₀ beam having an electrical field $E_{in} (\rho ,t)$ given by $E_{1} (\rho ,t)$ or $E_{2} (\rho ,t)$, respectively.

$$LG_{00} :E_{1} (\rho ,t) = E_{0} \times \exp \left[ { - \rho^{2} /W^{2} } \right] \times \exp \left[ { - t^{2} /\tau^{2} } \right],$$

(6)

$$LG_{10} :E_{2} (\rho ,t) = E_{0} \times \exp \left[ { - \rho^{2} /W^{2} } \right] \times \left[ {1 - 2\rho^{2} /W^{2} } \right] \times \exp \left[ { - t^{2} /\tau^{2} } \right],$$

(7)

where $\tau$ is the pulse duration.

The phase shift given by Eq. (4) is expressed as $\Delta \varphi_{1} (\rho ,t)$ ($\Delta \varphi_{2} (\rho ,t)$) for the LG₀₀ (LG₁₀) beam:

$$\Delta \varphi_{1} (\rho ,t) = \varphi_{0} \times \exp \left[ { - \frac{{2\rho^{2} }}{{W^{2} }}} \right] \times \exp \left[ { - \frac{{2t^{2} }}{{\tau^{2} }}} \right],$$

(8)

$$\Delta \varphi_{2} (\rho ,t) = \varphi_{0} \times \left( {1 - \frac{{2\rho^{2} }}{{W^{2} }}} \right)^{2} \exp \left[ { - \frac{{2\rho^{2} }}{{W^{2} }}} \right] \times \exp \left[ { - \frac{{2t^{2} }}{{\tau^{2} }}} \right].$$

(9)

Both beam LG₀₀ and LG₁₀ carry the same peak power $(\pi W^{2} E_{0}^{2} /2)$, and their transverse profiles are shown in Fig. 2. The LG₁₀ beam is made up of one central peak surrounded by a ring. The fraction of total power contained in the central peak is 26.3%.

Fig. 2

Transverse intensity distributions of the LG₀₀ (solid line) and LG₁₀ (dotted line) input beams for W = 1 mm

Before to address the problematic of temporal distortion of the pulse shape when subject to optical Kerr effect and focused, let us consider what can be considered as the source of the beam distortion. The latter is the phenomenon described above and called as “focal zoom” which will be characterised for both incidence (LG₀₀ and LG₁₀) at t = 0, namely at the pulse maximum. The first step is to calculate the diffracted on-axis intensity $I_{d} (0,z,t = 0)$ versus the longitudinal coordinate z, and the second step will consist to derive $z_{\max }$ the position of the best focus [maximum of $I_{d} (0,z,t = 0)$] as a function of the on-axis nonlinear phase shift $\varphi_{0}$. The results are shown in Fig. 3, and what is remarkable is the relative insensitivity of the LG₁₀ to the so-called “focal zoom” due to OKE. In contrast, the focused LG₀₀ beam subject to OKE is very sensitive to the focal zoom phenomenon. This property should be compared to the observed mitigation with regard to the spherical aberration shown for structured radial LG_p0 beams [18].

Fig. 3

Longitudinal position $z_{\max }$ of the best focus versus the nonlinear on-axis phase shift $\varphi_{0}$ for focused LG₀₀ and LG₁₀ beams subject to optical Kerr effect. The focusing lens has a focal length $f_{L} = 125\;{\text{mm}}$

It is interesting now to examine the variations of the on-axis intensity in plane $z = f_{L}$ at t = 0 for LG₀₀ or LG₁₀ incident beam versus the nonlinear on-axis intensity $\varphi_{0}$. The results are shown in Fig. 4 which clearly demonstrates that the LG₁₀ is highly resistant to the aberration due to OKE since its intensity remains close to the value without OKE ($\varphi_{0} = 0$). In contrast, the on-axis intensity $I_{d} (0,f_{L} ,t = 0)$ for the LG₀₀ declines significantly as $\varphi_{0}$ increases. For instance, for $\varphi_{0} = 4{\text{rad}}$ the on-axis intensity for the LG₁₀ beam is six times the intensity obtained with the LG₀₀ beam. In addition, it is seen in Fig. 4 unusual phenomenon since one can get more focused intensity when the LG₁₀ beam is subject to OKE than without OKE ($\varphi_{0} = 0$). We can speculate about the origin of this effect by considering the sign of the induced primary spherical aberration (SA) by the OKE (see Appendix). Indeed, it has already shown [19] that a lens with negative (positive) SA can achieve a smaller (larger) focused beam radius and a larger (smaller) maximum axial focused light intensity than without SA. Table 2 in Appendix shows that the primary SA coefficient A₁₁ is negative (positive) for the LG₀₀ (LG₁₀) beam. According to [19], it should be with the LG₀₀ beam that we should have observed an increased focused intensity. In fact, this apparent disagreement is due to the convention of sign used in [19] which is different from that used in the present work. Indeed, the minus sign appearing in the transmittance $\exp [ - i\Delta \varphi (\rho )]$ of the Kerr medium comes from the notation used for the wave propagation term written as $\exp [i(\omega t - knz)]$, where z is the distance covered in the Kerr medium of refractive index n. This minus sign influences directly the sign of the aberration coefficients when applying Eq. 18 in Appendix.

Fig. 4

Variations of the on-axis intensity in the focal plane $z = f_{L}$ versus $\varphi_{0}$ the on-axis nonlinear phase shift for focused LG₀₀ and LG₁₀ beams subject to optical Kerr effect

Now, to continue the study of the potential advantages to focus a LG₁₀ instead of a LG₀₀ beam, subject to OKE, we will now consider the longitudinal intensity distribution in the vicinity of plane $z = f_{L}$ at pulse maximum (t = 0). The results are shown in Figs. 5, 6 and 7. The case $\varphi_{0} = 0$ shown in Fig. 5 is given for reference purpose, and indicates that pure LG₀₀ and LG₁₀ beams after focusing produce the same on-axis intensity distribution as expected. However, as $\varphi_{0}$ is increased, it is shown in Figs. 6 and 7 that the best focus for the LG₀₀ is shifted toward the lens, and its intensity is reduced while the longitudinal distribution is broadened. In contrast, it is seen that the best focus of the LG₁₀ beam remains very close to the plane $z = f_{L}$ with a good focusing quality, namely a high intensity and a narrow on-axis distribution.

Fig. 5

On-axis intensity distribution of focused LG₀₀ and LG₁₀ beams without optical Kerr effect. The linear lens has a focal length f_L = 125 mm

Fig. 6

On-axis intensity distribution of focused LG₀₀ and LG₁₀ beams subject to optical Kerr effect for $\varphi_{0} = 2\pi$. The linear lens has a focal length f_L = 125 mm

Fig. 7

On-axis intensity distribution of focused LG₀₀ and LG₁₀ beams subject to optical Kerr effect for $\varphi_{0} = 4\pi$. The linear lens has a focal length f_L = 125 mm

Note that the longitudinal resolution in several applications such as prototyping techniques [20, 21] and nonlinear microscopy [22] is directly connected to the width (FWHM) of the peak of the on-axis intensity, i.e. the double of the Rayleigh distance. The latter one is much smaller for the LG₁₀ than for the LG₀₀ beam when subject to OKE as shown in Figs. 6 and 7. As a result, one can expect a better longitudinal resolution when using a LG₁₀ instead of a LG₀₀ beam for material processing using ultrafast lasers.

Few would doubt that the LG₁₀ beam is more resilient than the LG₀₀ beam when both are subject to optical Kerr effect. For confirmation of this, one needs to look no further than Figs. 4, 6 and 7. However, this conclusion is not definitive since it remains two key features to be discussed. The first one is the temporal distortion due to OKE of the on-axis intensity $I_{d} (0,z = f_{L} ,t)$ for the LG₀₀ and LG₁₀ beams. The second one concerns the shape of the transverse intensity distribution $I_{d} (r,z = f_{L} ,t = 0)$ at the pulse maximum.

2.1 Temporal distortion in the focal plane

It is known for a long time that the focusing of a pulsed Gaussian beam subject to OKE is characterised, in plane $z = f_{L}$, by an on-axis intensity showing a dip near the time corresponding to the peak of input pulse [15, 23]. Note that this temporal dip should increase with the nonlinear phase shift $\varphi_{0}$. This temporal dip is due to a lateral transfer of energy due the mechanism of beam reshaping through the diffraction phenomenon upon the phase profile $\Delta \varphi (\rho ,t)$. The consequence of this effect is a distortion in the transverse intensity profile which is no longer Gaussian in shape as it will be recalled in the next. The temporal evolution of $I_{d} (0,z = f_{L} ,t)$ without OKE is shown in Fig. 8 for reference purpose.

Fig. 8

Variations of the focused on-axis intensity of LG₀₀ and LG₁₀ beams in the focal plane versus the normalised time $t/\tau$, where $\tau$ is the pulse duration

Now, if we compare the temporal variations of the on-axis intensity in plane $z = f_{L}$ when the input pulse is a LG₀₀ or a LG₁₀ beam, displayed in Figs. 9 and 10, it must be recognised that the LG₁₀ beam shows a sensitivity to optical Kerr effect which is smaller than that of the Gaussian LG₀₀ beam. It can note that the temporal variation of the LG₁₀ focused on-axis intensity does not display the usual dip in intensity near the peak of input pulse observed with a LG₀₀ beam.

Fig. 9

Variations of the focused on-axis intensity of LG₀₀ and LG₁₀ beams in the focal plane versus the normalised time $t/\tau$, where $\tau$ is the pulse duration. The nonlinear on-axis phase shift is $\varphi_{0} = 2\pi$

Fig. 10

Variations of the focused on-axis intensity of LG₀₀ and LG₁₀ beams in the focal plane versus the normalised time $t/\tau$, where $\tau$ is the pulse duration. The nonlinear on-axis phase shift is $\varphi_{0} = 4\pi$

The last point to be examined concerns the distortion of the transverse intensity pattern in plane $z = f_{L}$ at time of maximum of the input pulse, i.e. t = 0.

2.2 Distortion of the transverse intensity profile in the focal plane

It is well known [24] that the radial intensity distribution in plane $z = f_{L}$ of the focused Gaussian LG₀₀ beam subject to OKE is made up of a central spot surrounded by concentric rings which number increases with $\varphi_{0}$, i.e. the pattern is no longer Gaussian in shape. The intensity profile in plane $z = f_{L}$ for $\varphi_{0} = 2\pi$[$\varphi_{0} = 4\pi$] is given in Fig. 11 [Fig. 13] for the $LG_{00}$ beam and in Fig. 12 [Fig. 14] for the $LG_{10}$ beam.

Fig. 11

Transverse intensity distribution, in the plane $z = f_{L}$, of the focused $LG_{00}$ beam subject to optical Kerr effect ($\varphi_{0} = 2\pi$)

The obvious conclusion from the consideration of Figs. 11, 12, 13, 14 is that the quality of focusing observed with a LG₁₀ beam subject to OKE is very much higher than that observed with the usual Gaussian LG₀₀ beam. The above conclusion is supported by two facts which are (i) the on-axis intensity in plane $z = f_{L}$ reached by the LG₁₀ beam is very much higher than that observed with the $LG_{00}$ beam, and (ii) the lateral extent of the focal spot observed for the $LG_{10}$ beam is narrower than that for the LG₀₀ beam. If these observations are added to the temporal behaviour of the LG₁₀ beam illustrated in Figs. 9 and 10, we can conclude that the use of a LG₁₀ beam is more advantageous than that of the usual LG₀₀ beam when both are subject to optical Kerr effect. It is worthwhile to point out that this conclusion was not foreseeable from the outset since the high-order transverse modes are deemed to be less bright than the usual Gaussian beam. However, the beam reshaping action due to the Kerr aberration $\Delta (\rho ,t)$ changes things somewhat. That superiority of the LG₁₀ over LG₀₀ beam subject both to OKE can be mainly explained by the value of the focal length associated with the Kerr lens due to the nonlinear phase shift $\Delta \varphi_{2} (\rho ,t)$ and $\Delta \varphi_{1} (\rho ,t)$. Indeed, as demonstrated in Appendix, at a given power the Kerr lens induced by a LG₀₀ beam is characterised by a focal length (in absolute value) smaller than that induced by a LG₁₀ beam. As a result, the focal shift for the LG₁₀ beam is less important than the one induced by the LG₀₀ beam so that the on-axis intensity in plane $z = f_{L}$ remains high even when $\varphi_{0}$ is relatively high.

Fig. 12

Transverse intensity distribution, in the plane $z = f_{L}$, of the focused $LG_{10}$ beam subject to optical Kerr effect ($\varphi_{0} = 2\pi$)

Fig. 13

Transverse intensity distribution, in the plane $z = f_{L}$, of the focused $LG_{00}$ beam subject to optical Kerr effect ($\varphi_{0} = 4\pi$)

Fig. 14

Transverse intensity distribution, in the plane $z = f_{L}$, of the focused $LG_{10}$ beam subject to optical Kerr effect ($\varphi_{0} = 4\pi$)

An important feature which has to be considered is the deposited energy, in plane $z = f_{L}$, per unit surface more commonly known as energy fluence, and noted $F(r)$ in the next. The latter is a quantity which is proportional to the number of photons received by surface unit, and is defined as the time-integrated flux of radiation and is written as follows

$$F(r) = \int\limits_{ - \infty }^{ + \infty } {I_{d} \left( {r,t,z = f_{L} } \right)\;} dt.$$

(10)

The transverse distribution of the energy fluence $F(r)$ takes into account the pulse stacking phenomenon since it expresses the number of photons deposited per unit surface integrated over the entire pulse. The results are shown in Fig. 15 (Fig. 16) for a LG₀₀ (LG₁₀) beam for a peak (at pulse maximum) nonlinear phase shift $\varphi_{0}$ equal to 0, $\pi$ and $2\pi$. It is seen very clearly that the behaviour of LG₀₀ and LG₁₀ beams having the same power, and subject to OKE is very different. Indeed, as $\varphi_{0}$ is increased it is seen a transfer of energy from the centre to the periphery for a LG₀₀ beam, and the opposite for a LG₁₀ beam. This result demonstrates that when subject to OKE the energy fluence of the focused LG₁₀ beam is not affected unlike the LG₀₀ beam. For the LG₀₀ beam, the energy fluence is reduced in the centre of the pattern while the latter is widened by the emergence of a pedestal leading certainly to a deterioration in the lateral resolution characterising the implemented laser processing. In contrast, the LG₁₀ beam is weathering the OKE better than the LG₀₀ beam since one observes in Fig. 16 a transfer of energy from the outer ring to the central peak. The energy fluence in the focal plane for the LG₁₀ beam is kept high despite the OKE, and this enabling a conservation of the lateral resolution.

Fig. 15

Variations of the energy fluence $F(r)$ in plane $z = f_{L}$ when the incident beam is a $LG_{00}$ beam for a nonlinear phase shift at pulse maximum $\varphi_{0} = 0$, $\pi$ and $2\pi$

Fig. 16

Variations of the energy fluence $F(r)$ in plane $z = f_{L}$ when the incident beam is a $LG_{10}$ beam for a nonlinear phase shift at pulse maximum $\varphi_{0} = 0$, $\pi$ and $2\pi$

A question remains which is how to force the fundamental mode of a laser to be a LG₁₀ instead of the usual LG₀₀ mode. Forcing the LG₁₀ mode to be the fundamental mode, i.e. the first mode reaching the oscillation threshold, can be achieved by imposing the position of the zero of intensity which defines the associated ring. This can be achieved by inserting a phase [25,26,27] or amplitude mask inside the laser cavity [28,29,30,31,32]. It should be noted that forcing a laser to oscillate in a mode-locking regime by Kerr lens mode locking (KLM) on a single transverse LG₁₀ mode still remains a challenging issue. However, it is possible to make the transformation from a LG₀₀ to a LG₁₀ beam outside the laser cavity using a simple binary diffractive element [33], made up of one π-phase discontinuity, before to be collimated and sent into the amplifier stages.

As shown in Eq. (26) from Appendix, the Kerr lens induced by a LG₁₀ beam has a negative focal length unlike for the case of a Gaussian beam when $n_{2} > 0$. This means that the self-action induced by a LG₁₀ beam inside a Kerr medium should be qualified as self-defocusing instead of self-focusing. This may open some interesting new insights into the propagation of intense short pulses in a Kerr medium. Indeed, the pulse propagation could be done without the usual phenomenon of beam collapse observed with a Gaussian beam, and that could probably extend the upper limit of the laser intensity in high power laser systems. However, we have to be careful with regard to this very promising property of the LG₁₀ beam because we should also take into account the possible small-scale self-focusing effect linked with ring of light located in its trailing edges. This particular phenomenon is an amplification mechanism of intensity fluctuations described in details in chap. 6 of Ref. [14].

3 Focusing a super-Gaussian beam subject to OKE

To reduce the multiple bad consequences of the self-focusing in high-peak-power laser chains, it has been proposed by some authors the use of a super-Gaussian laser beam instead of the usual Gaussian beam. This point of view is well developed in chap. 8 of Ref. [14]. However, one can notice in literature, to the best of our knowledge, a lack of studies regarding the Kerr lensing effect and aberrations induced by a super-Gaussian laser beam subject to OKE. The aim of this paper is to tackle this subject by considering the focusing quality affected by this Kerr lensing to evaluate the efficiency of structuring the laser beam along a super-Gaussian intensity profile.

Before to proceed let us introduce the intensity profile $I_{SG} (\rho )$ characterising the incident super-Gaussian (SG) laser beam having an on-axis intensity $I_{0SG}$, and a width W = 1 mm

$$I_{{{\text{SG}}}} (\rho ) = I_{{{\text{0SG}}}} \exp \left[ { - 2\left( {\frac{\rho }{W}} \right)^{2N} } \right],$$

(11)

where N is some integer designing the SG order. The standard Gaussian beam is obtained for N = 1. As the SG order increases, the intensity profile becomes more and more squared. For N very large, the SG beam may be regarded as a flat-top (FT) beam characterised by the following intensity distribution:

$$I_{FT} = \left\{ \begin{gathered} I_{0SG} \quad \rho \le W \hfill \\ 0\quad \rho > W \hfill \\ \end{gathered} \right..$$

(12)

An important feature useful to note is that the Gaussian beam maintains its shape in free space as it propagates, while it changes continuously for N > 1. The propagation and focusing properties of a super-Gaussian beam subject to OKE is based on an interplay between nonlinear effects and linear diffraction. To be able to compare the induced aberrations and lensing effects when the super-Gaussian order N is varied, it is assumed that all considered beams carry the same power P. Consequently, the first thing to be done is to determine the power P carried by the super-Gaussian beam expressed in Eq. (11):

$$P = 2\pi \int\limits_{0}^{\infty } {I_{SG} (\rho )\rho d\rho } .$$

(13)

The solution of the integral given by Eq. (13) can be found in Ref. [34] and takes the following form

$$P = \frac{{\pi W^{2} I_{{{\text{0SG}}}} }}{2}\frac{\Gamma (1/N)}{{N \times 2^{{\left( {\frac{1 - N}{N}} \right)}} }} = \frac{{\pi W^{2} I_{{{\text{0SG}}}} }}{2} \times K,$$

(14)

where $\Gamma$ is the gamma function, and K a weighting factor expressed as follows and given by Table 1

$$K = \frac{\Gamma (1/N)}{{N \times 2^{{\left( {\frac{1 - N}{N}} \right)}} }}.$$

(15)

Table 1 Variations of coefficient K given by Eq. (15) versus the super-Gaussian order N

Note that the quantity $\pi W^{2} I_{0SG} /2$ in Eq. (14) represents the power carried by a Gaussian beam having a width W, and an on-axis intensity $I_{0SG}$.

Let us return to the Kerr phase shift profile given by Eq. (3) which can be written as follows:

$$\Delta \varphi (\rho ) = \varphi_{0} K\exp \left[ { - 2\left( {\frac{\rho }{W}} \right)^{2N} } \right],$$

(16)

where $\varphi_{0}$ is the nonlinear on-axis phase shift, given by Eq. (4), for the Gaussian case (N = 1) which can be considered for reference purpose [13] in term of Kerr lensing effect.

As discussed in the previous section, the origin of the spatiotemporal distortion of the focused laser beam subject to OKE is the focal zoom effect. Consequently, for sake of simplicity, we will examine the focal shift by considering the position of the best focus (maximum of on-axis intensity) versus the nonlinear phase shift $\varphi_{0}$ for various super-Gaussian order N. For that, we will not take into account the temporal evolution of the laser pulse. The calculations of the best focus position and intensity in plane $z = f_{L}$ are made at t = 0, namely at the pulse maximum. The results are shown in Fig. 17 which displays the best focus position versus the phase shift $\varphi_{0}$, and the following should be recognised. In contrast with what could be expected, it is observed that the focal zoom phenomenon is more (less) pronounced for N > 1 than for the Gaussian case for $\varphi_{0} < 5\pi$ ($\varphi_{0} > 5\pi$). As a consequence, there is a little interest in using a laser beam having a super-Gaussian intensity profile with the hope to reduce the focal zoom phenomenon induced by OKE and its consequences. It is clear that the comparison of Fig. 17 with Fig. 3 serves to establish that the $LG_{10}$ beam is quite superior to the SG beam to mitigate the Kerr focus shift effect that is causing the reduction of intensity in the geometric focal plane $z = f_{L}$.

Fig. 17

Variations of $z_{\max }$ the longitudinal position of the best focus point versus the non-linear on-axis phase shift $\varphi_{0}$.for several values of the super-Gaussian order N

From the point of view of intensity reduction in plane $z = f_{L}$ due to OKE, the plots of $I_{d} (0,f_{L} )$, for various value of N, displayed in Fig. 18 shows that we have a strong interest in using short laser pulses having a super-Gaussian rather than the usual Gaussian intensity profile. However, it is also clear that the plots in Fig. 4 demonstrate that the $LG_{10}$ beam has the best performance over the Gaussian and super-Gaussian, at least until N = 6, for resisting to the Kerr focus shift effect which is at the origin of the intensity reduction in plane $z = f_{L}$. It is worthwhile to recall that a super-Gaussian or top-hat beam is not shape-invariant as it propagates except if the beam is collimated. A detailed study of such beams can be found in [35].

Fig. 18

Variations of the on-axis intensity in the geometrical focal plane $z = f_{L}$ versus the nonlinear on-axis phase shift for various super-Gaussian order N

Now it remains to examine the behaviour of the energy fluence for various super-Gaussian orders N. The results are shown in Figs. 19, 20, 21, for N = 3, 6 and 9, respectively. Note that the power of the incident beam is the same whatever the incident beam.

Fig. 19

Variations of the energy fluence $F(r)$ in plane $z = f_{L}$ when the incident beam is a super Gaussian beam of order N = 3 for a nonlinear phase shift at pulse maximum $\varphi_{0} = 0$, $\pi$ and $2\pi$

Fig. 20

Variations of the energy fluence $F(r)$ in plane $z = f_{L}$ when the incident beam is a super Gaussian beam of order N = 6 for a nonlinear phase shift at pulse maximum $\varphi_{0} = 0$, $\pi$ and $2\pi$

Fig. 21

Variations of the energy fluence $F(r)$ in plane $z = f_{L}$ when the incident beam is a super Gaussian beam of order N = 9 for a nonlinear phase shift at pulse maximum $\varphi_{0} = 0$, $\pi$ and $2\pi$

As expected, we find that a super-Gaussian beam at least of order N = 6 is weathering the OKE better than the LG₀₀ beam. When subject to OKE, it is seen that the super-Gaussian beam achieves a higher fluence than the Gaussian beam (N = 1) at a given incident power. However, without OKE the highest energy fluence is obtained with the usual LG₀₀ beam. Nevertheless, after having compared Figs. 15, 16, 19, 20 and 21, we are able to conclude that for a given power, from among the laser beams LG₀₀, LG₁₀, and super-Gaussian subject to OKE, it is the LG₁₀ beam which is able to generate the highest energy fluence after being focused.

Lastly, we are going to discuss briefly the production of a laser beam having a super-Gaussian intensity profile. This problematic is almost as old as the emergence of lasers, and is the focus of intense investigations which are still going today. Without going into further details, it should be mentioned that for obtaining a laser beam having a SG profile there are two families of techniques:

• 1. Intra-cavity beam shaping: one or two diffracting optical elements (DOE) are inserted inside the laser cavity so that the eigenmode is no longer Gaussian in shape but rather super-Gaussian [36].

• 2. External laser beam shaping: outside the laser cavity delivering a Gaussian beam which is reshaped into a super-Gaussian beam thanks the use of one or two DOE [37, 38].

4 Conclusions

We have considered theoretically the focusing properties of three laser beam types subject to optical Kerr effect (OKE). The first one is the well-known LG₀₀ (Gaussian) beam, the second is the super-Gaussian (SG) of order N, and the third is the LG₁₀ beam. The three beams are assumed to have the same power. The OKE gives rise to the phenomenon of Kerr lensing effect having the consequence to shift the position of the best focus where the on-axis intensity is maximum. This Kerr lensing effect contributes to reduce the intensity in the reference plane $z = f_{L}$, the geometric focal plane of the focusing lens of focal length $f_{L}$. It is observed that the focal shift due to the OKE is reduced as the super-Gaussian order N is increased. However, it must be concluded that the radial Laguerre–Gauss LG₁₀ beam is almost completely insensitive to OKE since the best focus shifting is so small that the intensity in plane $z = f_{L}$ remains as high as without OKE.

From the Appendix (see Eq. 26), it can be said that the self-action of a LG₁₀ beam inside a Kerr medium should be qualified as self-defocusing instead of self-focusing even though the nonlinear refractive index $n_{2}$ is positive. This may open some interesting new insights into the propagation of intense short pulses in Kerr medium. Indeed, the latter could be without the usual phenomenon of beam collapse observed with a Gaussian beam, and that could probably extend the upper limit of the laser intensity in high-power laser systems. However, we have to be careful with regard to this very promising property of the LG₁₀ beam because we should also take into account with the small-scale self-focusing effect linked with ring of light located in its trailing edges.

We believe that these results allow overcoming the spatiotemporal distortions induced by optical Kerr effect when focusing a laser beam. That would be helpful for the user community of high power lasers delivering ultra-short pulses, in particular for the processing of materials using ultrafast lasers which requires a high focusing quality.

For the sake of simplicity, we have omitted in our study a certain number of phenomena such as linear dispersion, self-phase modulation, spectrum modification which in general play an important role in the propagation of intense ultra short pulses. It could be then interesting to consider their influence on the focusing properties of laser beams subject to Kerr effect.

Appendices

Appendix

Kerr lens modelling for LG₀₀ and LG₁₀ beams

In the next, we will present a modelling of the Kerr lensing effect induced by LG₀₀ and LG₁₀ based on the Zernike polynomial decomposition. The propagating term of the collimated incident beam emerging from the Kerr medium is written $\exp \left[ {ikW(\rho )} \right]$, where $kW(\rho ) = - \Delta \varphi (\rho )$. The phase distribution $W(\rho )$ is usually called as wave aberration function (WAF) according to the terminology of optical aberration modelling [39]. The WAF is expanded as a linear combination of Zernike polynomials (ZP), $Z_{j}$, as follows

$$W(\overline{\rho }) = \sum\limits_{j = 1}^{\infty } {a_{j} Z_{j} (} \overline{\rho })$$

(17)

where the index j is a polynomial-ordering number, and $a_{j}$ the aberration coefficients. The normalised radial coordinate $\overline{\rho }$ is equal to $\rho /R$, where R is the radius of the unit circle. In the following we set R equal to 1.5 W (2.5 W) since the circle of radius 1.5 W (2.5 W) contains 99% of the incident LG₀₀ (LG₁₀) beam power. The Zernike polynomials $Z_{j} (\overline{\rho },\theta )$ are a set of orthogonal functions over the unit circle ($0 \le \overline{\rho } \le 1$). Table 2 gives the corresponding ZP’s [40].

Table 2 Zernike polynomials allowing to calculate the four-first non-zero aberration coefficients $a_{1}$, $a_{4}$, $a_{11}$ and $a_{22}$

For the calculation of the aberration coefficient $a_{j}$.we will take into account the amplitude profile $E(\rho )$ of the incident beam [41]:

$$a_{j} = \frac{{ - \int\limits_{0}^{1} {E(\overline{\rho })\Delta \varphi (\overline{\rho })Z_{j} (\overline{\rho })\overline{\rho }d\overline{\rho }} }}{{k\int\limits_{0}^{1} {E(\overline{\rho })\overline{\rho }d\overline{\rho }} }}$$

(18)

where $E(\overline{\rho })$ stands for $E_{1} (\overline{\rho })$, when the incident beam is a LG₀₀ and $E_{2} (\overline{\rho })$ for a LG₁₀:

$$E_{1} (\overline{\rho }) = E_{0} \times \exp \left[ { - 2.25\overline{\rho }^{2} } \right] \times \exp [ - t/\tau ],$$

(19)

$$E_{2} (\overline{\rho }) = E_{0} \times \left[ {1 - 9.68\overline{\rho }^{2} } \right]\exp \left[ { - 4.84\overline{\rho }^{2} } \right] \times \exp [ - t/\tau ].$$

(20)

The nonlinear phase shift $\Delta \varphi (\overline{\rho })$ stands for $\Delta \varphi_{1}$ and $\Delta \varphi_{2}$, given by Eqs. (8) and (9), and by taking into account the normalisation of the radial coordinate rewrite as

$$\Delta \varphi_{1} (\overline{\rho }) = \varphi_{0} \times \exp [ - 4.5\overline{\rho }^{2} ],$$

(21)

$$\Delta \varphi_{2} (\overline{\rho }) = \varphi_{0} \times [1 - 12.5\overline{\rho }^{2} ]^{2} \times \exp [ - 12.5\overline{\rho }^{2} ].$$

(22)

The sum in Eq. (17) is infinite, but is usually truncated. Here, we will work arbitrarily until j = 22, and because of the rotational symmetry of $\Delta \varphi$ most of coefficients $a_{j}$ are equal to zero except four of them: a₁, a₄, a₁₁ and a₂₂.

In the following, we will use the dimensionless aberration coefficients A_j which are expressed in unit of wavelength, and is defined as $A_{j} = a_{j} /\lambda$. By taking into account the expressions of $E(\overline{\rho })$ and $\Delta \varphi (\overline{\rho })$ we get finally.

For LG₀₀:

$$A_{j} = \frac{{ - \varphi_{0} \int\limits_{0}^{1} {\overline{\rho }\exp [ - 6.75\overline{\rho }^{2} ]} Z_{j} (\overline{\rho })d\overline{\rho }}}{{2\pi \int\limits_{0}^{1} {\overline{\rho }\exp [ - 2.25\overline{\rho }^{2} ]} d\overline{\rho }}}.$$

(23)

For LG₁₀:

$$A_{j}^{\prime } = \frac{{ - \varphi_{0} \int\limits_{0}^{1} {\overline{\rho }[1 - 12.5\overline{\rho }^{2} ]^{3} \exp [ - 18.75\overline{\rho }^{2} ]} Z_{j} (\overline{\rho })d\overline{\rho }}}{{2\pi \int\limits_{0}^{1} {\overline{\rho }[1 - 12.5\overline{\rho }^{2} ]\exp [ - 6.25\overline{\rho }^{2} ]} d\overline{\rho }}}.$$

(24)

The integrals in Eq. (23) and (24) are solved numerically using a FORTRAN routine based on the numerical integrator dqdag from the International Mathematics and Statistical Library (IMSL). The results are given in Table 3:

Table 3 Dimensionless aberrations coefficients $A_{1}$,$A_{4}$,$A_{11}$ and $A_{22}$ normalised by the nonlinear axis phase shift $\varphi_{0}$ associated with the Kerr phase aberration $\Delta \varphi_{1} (\rho )$ or $\Delta \varphi_{2} (\rho )$, when the input is a LG₀₀ or a LG₁₀ beam, respectively

It has been already shown [42] that it is possible to deduce an equivalent focal length $\sqrt 3 R^{2} /(12\lambda A_{4} )$, noted $f_{K0}$, for LG₀₀ input, and $f_{K1}$, for LG₁₀ input, from the aberration coefficients $A_{4}$ and $A_{4}^{^{\prime}}$:

For LG₀₀:

$$f_{K0} = \frac{{4.48W^{2} }}{{\lambda \varphi_{0} }} \times \exp [2(t/\tau )^{2} ],$$

(25)

For LG₁₀:

$$f_{K1} = \frac{{ - 84W^{2} }}{{\lambda \varphi_{0} }} \times \exp [2(t/\tau )^{2} ].$$

(26)

The first remark that could be made from the above is that the Kerr lensing effect induced by a LG₀₀ (LG₁₀) is a converging (diverging) lensing effect which has a tendency to shift the best focus point toward (away) the lens. In addition, Eqs. (25) and (26) show that $\left| {f_{K1} } \right| > > \left| {f_{K0} } \right|$ and that explains the focal shift behaviour illustrated in Fig. 3.

The position $z_{F0}$ ($z_{F1}$) of the best focus when the input is a LG₀₀ (LG₁₀) beam in the framework of the above Kerr lens modelling is given by

$$\frac{1}{{z_{F0} }} = \frac{1}{{f_{L} }} + \frac{1}{{f_{K0} }}\,{\text{and}}\,\frac{1}{{z_{F1} }} = \frac{1}{{f_{L} }} + \frac{1}{{f_{K1} }}.$$

(27)

The results are shown in Fig. 17, for t = 0, which displays the best focus position $z_{F0}$ and $z_{F1}$, resulting from the above Kerr lens modelling for LG₀₀ and LG₁₀ input, and position $z_{\max }$ calculated from the on-axis intensity distribution. The agreement between the Kerr lens modelling ($z_{F0}$ and $z_{F1}$) and the position $z_{\max }$ of the best focus is not perfect but satisfactory at the very least concerning the trend in focus shift due to optical Kerrr effect (Fig. 22).

Fig. 22

Comparison of the best focus position obtained (i) by solving the diffraction integral ($z_{\max }$) and (ii) by the Kerr lens modelling based on the aberration coefficients characterising the Kerr phase profile induced by LG₀₀ and LG₁₀ beams ($z_{F0}$ and $z_{F1}$)

Validity of Fresnel–Kirchhoff integral for ultrashort pulses

The well-known Fresnel–Kirchhoff integral given by Eq. (5) assumes that the incident wave is monochromatic, and this is rigorously not the case when the incident beam is an ultrashort pulse. The time variation of the electric field associated with the laser pulse takes the following form

$$E(t) = \exp \left[ { - t^{2} /\tau^{2} } \right] \times \exp (i\omega_{0} t).$$

(28)

The spectral content $E(\omega )$ is deduced from the following Fourier transform

$$E(\omega ) = \tau \sqrt \pi \times \exp \left[ { - \pi^{2} \tau^{2} (\omega - \omega_{0} )^{2} } \right].$$

(29)

The spectral width (at half-maximum) is equal to $\Delta \omega = \sqrt {\ln 2} /(\pi \tau )$. If one considers a central wavelength $\lambda_{0} = 1064nm$ we obtain the width $\Delta \lambda$ of the spectral distribution

$$\frac{\Delta \lambda }{{\lambda_{0} }} = \frac{{0.149 \times 10^{ - 15} }}{\tau }.$$

(30)

If one takes into account Eq. (4), we can estimate the variation $\Delta \varphi_{0}$ of the nonlinear on-axis phase shift which is the key parameter of the diffracted field distribution:

$$\frac{{\Delta \varphi_{0} }}{{\varphi_{0} }} = \frac{\Delta \lambda }{{\lambda_{0} }} = \frac{{0.149 \times 10^{ - 15} }}{\tau }.$$

(31)

The following table (Table 4) shows that for a pulse duration $\tau > 100fs$, the resulting variation of the nonlinear on-axis phase shift is too small for having a significant influence on the diffracted field. As a result, in these conditions we can use the classical Fresnel–Kirchhoff integral for calculating the pattern in plane $z = f_{L}$.

Table 4 Relative variations of the nonlinear phase shift due to the spectral content of the pulse of duration $\tau$

In the case where the pulse duration $\tau$ is too short, the application of Eq. (4) is not valid and the calculation of the diffracted field should need to take into account the finite spectrum.