1 Introduction

Although the non-diffraction characteristic of Bessel–Gaussian beams (BGBs) [1,2,3] has opened new horizons in various fields, the higher order transverse modes (HOTM) of BGBs have also attracted much attention in the past few years thanks to their dark central core and no spatial change in their profile while they propagate through a medium [4,5,6,7,8,9,10]. For instance, BGBs of higher orders are promising for atom trapping owing to their zero axial intensity and large gradient of intensity [11]. High-power HOTM of BGBs have many industrial applications; however, their generations and their mode distinguishability are a challenge for experimentalists [5]. So far, various methods have been reported for their production including holographic elements [12, 13], axicon-type computer generated holograms [13, 14] and the passage of Laguerre–Gaussian beams through an axicon prism [15]. Nowadays, high-power Bessel–Gaussian lasers (>10 W) with HOTMs have attracted much attention due to their extensive applications in basic science such as laser ablation [16], trimming [17], bio-physics [18], surface nano-processing [19], laser micro-drilling technology [20] and micro-machining [10, 21,22,23]. Overcoming the problem of controlling the internal structure of dielectric materials with high-power femtosecond lasers is another scientific application of the HOTM of BGBs [22]. In general, there are two different methods to produce HOTM of BGBs, namely extra-cavity (passive) [15] and intra-cavity (active) [24] methods. In the passive arrangement, one needs to transmit the HOTM of the Gaussian beam through an axicon prism, while in the active arrangement, the resonator directly generates non-diffractive beams without using any external optical elements [15, 24]. The advantages of the active method or the so-called ‘axicon-based resonator’ included high reliability and beam quality, great simplicity and better power efficiency in high-power regimes.

Despite these advantages, only a few researchers have utilized the active method to generate high-power BGBs. Khilo et al. presented a special optical resonator to produce only a low-power zero-order BGBs [25]. Using the active method, Singh et al. managed to generate a high-power zero-order BGBs in the visible region from a copper vapor laser with the output power of 31 W. Their noticeable laser properties were their low divergence and focus ability [24]. Using an axicon-based resonator, Wu et al. presented a Q-switched Nd:YAG laser rather simple but with merely zero-order BG pulses with durations of about 30–40 ns [26]. To the best of the authors’ knowledge, only the zero-order of high-power BGBs obtained from an active resonator has been addressed in the literature.

In this work, two types of high-power lasers, CW and Q-switched regimes, have been designed to produce higher order modes. The main challenges in producing high-power and high-order of BGBs are the damage threshold of the optical elements and the control of the beam shape. These challenges can be solved to some extent using an axicon-based resonator.

The acceptable and proper compliance between the theoretical and the experimental results of the current study shows that the proposed method can be effectively used for designing reliable sources for high-power and high-order BGBs. This paper is structured as follows: in Sect. 3, the theory behind the experimental results is described. In Sect. 3, using the active method, the high-power and high-order selective modes of BGBs in CW and Q-switched lasers are theoretically and experimentally obtained. In Sect. 5, the HOTMs of BGBs are obtained using the passive method and its results are compared with those of the active method. The discussion is given in Sect. 6. The last section is dedicated to the concluding remarks.

2 Generalized model for selective transverse modes in axicon-based resonators (active method)

In this section, a theoretical description of the HOTMs of BGBs is presented by designing an axicon-based resonator. Generally, the output field of a laser resonator can be calculated using Collins diffraction integral. If \(E_1 (\rho _1)\) is assumed to be the initial field amplitude on the output mirror, according to Collins diffraction integral, the field amplitude, \( E_1^{'} (\rho _1^{'} )\), after one round-trip in the resonator, is calculated as [27]:

$$\begin{aligned} \begin{aligned} E^{\prime }_{1} (\rho ^{\prime }_{1} )&= \frac{{( - 1)^{{n + 1}} k\exp (ikL)}}{B}\int _{0}^{{r_{{\text {b}}} }} {E_{2} } (\rho _{2} )T(\rho _{2} ) \\&\quad J_{n} \left( {\frac{{k\rho ^{\prime }_{1} \rho _{2} }}{B}} \right) \exp \left[ {\frac{{ik}}{{2L}}[A\rho _{2}^{2} + D\rho _{1}^{{\prime 2}} ]} \right] \rho _{2} {\text {d}}\rho _{2}, \\ \end{aligned} \end{aligned}$$
(1)

in which, \(E_2\) is the field amplitude incident on the back mirror expressed as

$$\begin{aligned} \begin{aligned} E_{2} (\rho _{2} )&= \frac{{( - 1)^{{n + 1}} k\exp (ikL)}}{B}\int _{0}^{{r_{{\text {a}}} }} {E_{1} } (\rho _{1} )J_{n} \left( {\frac{{k\rho _{1} \rho _{2} }}{B}} \right) \\&\quad \exp \left[ {\frac{{ik}}{{2B}}[A\rho _{1}^{2} + D\rho _{2}^{2} ]} \right] \rho _{1} {\text {d}}\rho _{1} , \\ \end{aligned} \end{aligned}$$
(2)

where \(r_{{\text {a}}}\) and \(r_{{\text {b}}}\) are the radius of aperture ‘a’ and ‘b’, respectively, L is the resonator length, k is the wave number, A, B, D are the ray transfer matrix elements for the propagation in the resonator, and \(J_n\) is the nth order of Bessel function. In this study, the axicon double-pass transmission function (\(T(\rho _2)\)) which is calculated by \(\exp [-2ik \theta \rho _2]\) is used for the axicon-based resonator. In this relation, \(\theta =(N-1)\gamma \) is the beam conical angle, N is the refractive index, and \(\gamma \) is the axicon base angle. It should be noted that the initial field amplitude, \(E_1\), is an mth-order Bessel–Gaussian beam given by

$$\begin{aligned} E_{1} (\rho _{1} ) = AJ_{n} (\alpha \rho _{1} )\exp ( - \rho _{1}^{2} /w_{0}^{2} )\exp (in\phi ), \end{aligned}$$

where \(\alpha = k \sin \theta \) is \(25.7665 \times 10^{-3}\) \(m^{-1}\) (the transverse wave number) [2, 5, 28], parameter n in the \(J_n\), as the nth order of Bessel function, can be start from zero (for zero-order Bessel–Gaussian beam mentioned by Gori et al. [2]) to upper numbers (for high-order Bessel Gaussian beams mentioned by [25, 29, 30]), \(\exp (in\phi )\) is the phase term for the beam and \(w_0\) is the Gaussian beam waist. It can be seen that the radius of the input Gaussian beams to the axicon has a special role in the mode order of the BGBs. By keeping the other parameters of the laser constant, the reduction in the radius of the input Gaussian beam to the axicon increases the mode order of the output BGBs. In the current research, the aperture “a” is placed in the resonator in such a way that it is located in front of the axicon, hence is mainly responsible to control the radius of the Gaussian beam illustrated the axicon. Thus, its size and location are the key factors with the aim of obtaining the orders of HOTML of BGBs.

Notably, some parameters such as aperture size, axicon base angle and the optical parameters of the resonator have vital influence on the presence of various orders of multi-pass Bessel–Gaussian modes [25, 31].

3 Experimental results of the axicon-based resonator

The experimental parts of the current research are organized as follows: initially, using a simulation derived from the theory presented in the previous section, a high-power CW active resonator is set up to observe the fundamental mode. Then the effects of the resonator optical length and the aperture size on the Bessel–Gaussian transverse mode selection are theoretically investigated and experimentally verified in Sects. 3.2 and 3.3, respectively. Afterward, a high-power Q-switched active resonator is set up for investigating the same effects in Sect. 4. It is necessary to mention that the focal length of the thermal lens has small value with destructive impact on the transverse mode selection of high-power lasers. Controlling and considering these effects in simulations make it possible to have a precise prediction of the mentioned laser parameters for obtaining the HOTM of BGB. Therefore, this thermal lens can be employed as an optical lens in the resonator. Thus, due to this effect, plane mirrors are used in this research [28].

3.1 Selective transverse mode of BGB by optimizing the resonator length

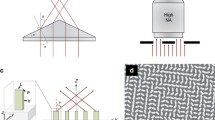
In this section, by changing and optimizing the resonator length, the selective transverse mode becomes possible. For this purpose, aperture “a” is not used (means is opened completely), while aperture “b” is used to eliminate the transverse mode noises (small low intensity peaks around the main peak) and to increase the beam quality factor. Figure 1 shows the experimental setup for generating a high-power CW-BGBs which is investigated using a 3 × 60 mm, \( 0.8\% \)-dope Nd:YAG rod side-pumped by a 320 W diode laser. The thermal focal length of crystal is measured as 350 mm.

Fig. 1
figure 1

The schematic diagram of the high-power CW laser for the selective transverse mode of the BGB. In this diagram, \(d_1\) = \(d_2\) = 20 mm, \(L_{{\text {c}}}\) = 60 mm and the rod diameter is 3 mm

Full size image

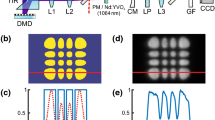
A axicon plane-mirror prism (with the apex angle (\(\Omega \)) of \(179 ^{\circ }\) or base angle (\(\gamma \)) of \(0.5 ^{\circ }\) [28]) has been used as the back mirror and a partially reflective mirror (\( 80\% \)) has been employed as the output coupler. A standard CCD at a distance of 15 mm from the output coupler observes the intensity profiles of the BGBs. The optimum length of the resonator and the output power of the fundamental mode (\(J_0\)) are obtained as about 100 mm and 84 W, respectively. The resonator lengths of 160 and 210 mm would allow the extraction of \(J_5\) (with the output power of 69 W) and \(J_{10}\) (with the output power of 51 W) transverse modes, respectively. The theoretical and experimental results are compared in Fig. 2 to ensure that they are indeed in good agreement with each other. Table 1 tabulates the optimized resonator length for fundamental and two other higher order modes of BGBs.

Table 1 The experimental data showing the output parameters of the CW laser with their corresponding to laser length
Full size table
Fig. 2
figure 2

The theoretical and experimental transverse modes ((I) for 1D and (II) for 2D) of the BGBs produced by the resonator length of a 100 mm, b 160 mm and c 210 mm at a distance of 15 mm from the output mirror

Full size image

3.2 Selective transverse modes of CW BGBs by optimizing the aperture radius

In this section, The HOTMs of BGBs in the active method are selected directly from the resonator. This is done only by adjusting and optimizing the location and radius of the intra-cavity apertures, as key factor, without changing optical resonator length. The laser cavity, output coupler, and pump power parameters are chosen similar to those in Sect. 3.2. The setup schematic is the same as the one in Fig. 1 in which two variable apertures (“a” and “b”) are employed. In addition, the resonator optical length is fixed at 100 mm. As shown in Fig. 3, the experimental results of high-power and high-order Bessel–Gaussian laser easily confirm by the theoretical results for transverse mode of BGB in \(J_{10}\) and \(J_5\) modes. The results summarized in Table 2 show that decrease (increase) of the radius of aperture “a”, increase (decrease) the order of the transverse mode owing to the location of this aperture. By tuning the aperture radius to \(r_{{\text {a}}}= 2, 1\) and 0.7 mm, \(J_0\), \(J_5\), and \(J_{10}\) are obtained for which the output powers are measured as 84, 64, and 58 W, respectively. It is worth mentioning that the first stage of the tuning mode by the aperture is accomplished by maximizing the output power of the laser in the zero-order mode.

It should be noted that the reduction of the axicon aperture results in decreasing the Rayleigh range of the BGBs. In other words, in this situation, the round-trips of the low-order modes become impossible; therefore, without doubt, the HOTM of BGBs is generated in this method. Using the optimization of the aperture method instead of the optimization of resonator length method, a more convenient and compact setup (producing a higher quality beam) is achievable. Even so, power efficiency in this method in mostly less than earlier method (Sect. 3.2).

Table 2 The experimental data showing the results of optimized aperture radius “\(r_{{\text {a}}}\)” (CW laser)
Full size table
Fig. 3
figure 3

The theoretical and experimental transverse modes ((I) for 1D and (II) for 2D) of the BGBs using aperture in the CW laser for a \(J_5\), \(r_{{\text {a}}} = 1\) mm and b \(J_{10}\), \(r_a = 0.7\) mm at the distance of 15 mm from the output coupler

Full size image

3.3 Selective transverse modes of high-power Q-switched laser

The effect of the resonator length and iris aperture on selection transverse modes of BGBs for a pulsed laser is reported in this section. Since high-power Q-switched lasers [32,33,34,35,36] have more applications than continuous lasers mentioned above, the selective transverse modes of BGBs in high-power pulsed lasers are explored. Similar to the CW laser mentioned in Sect. 3.3, the transverse mode selection is obtained only by an intra-cavity aperture. The resonator length is optimized for fundamental mode \(J_0\) with open aperture and is fixed at 135 mm. To do the experiments, a diode pumped Nd:YAG laser is set up with the configuration shown in Fig. 4. A 65-mm-long crystal rod with the diameter of 4 mm is side-pumped with a peak power of 3.6 kW at 210 μs and up to 10 Hz repetition rate. A axicon plane-mirror with the base angle of \(0.5^{\circ }\) and an output plane mirror with the reflectivity of \(30\%\) are used. A 9 × 9 × 25 \(mm^{3}\) Li:NBO3 electro-optical crystal together with a suitable polarizer (\(Tp/Ts>300\)) is placed into the resonator. The input voltage on the Q-switched crystal is assumed to be at most 1.8 kV with the time duration of 40 ns. The focal length of the thermal lens is measured to be more than 8000 mm at 10 Hz with \(25^{\circ }C\) water cooling apparatus. The pulse duration of the laser is 10 ns.

Fig. 4
figure 4

The schematic of the high-power Q-switched Bessel–Gaussian laser (\(d_1=d_2=d_4=10\) mm, \(d_3=15\) mm, \(L_{{\text {c}}}=65\) mm and \(L_{{\text {Q}}}=25\) mm)

Full size image

Now, by fine-tuning of aperture “a” various HOTMs of the BGBs are obtained. The iris radii of the aperture for the modes \(J_0\), \(J_5\) and \(J_{10}\) are \(r_{{\text {a}}}\) = 2.5, 1.5 and 1.2 mm, respectively. The output energies of \(J_0\), \(J_5\) and \(J_{10}\) are 91, 75 and 61 mJ, respectively (Table 3). Figure 5 shows again very good agreement between the theoretical and experimental results for the \(J_5\) and \(J_{10}\) modes. The results in Table 3 and Fig. 5 indicate that the decrease of the radius of aperture “a” increases the order of the transverse mode as observed in Sect. 3.3.

Fig. 5
figure 5

Experimental and theoretical transverse modes ((I) for 1D and (II) for 2D) of the BGBs using aperture in the Q-switched pulsed laser for a \(J_5\), \(r_{{\text {a}}}\) = 1.5 mm and b \(J_{10}\), \(r_{{\text {a}}}\) = 1.2 mm

Full size image
Table 3 The experimental data showing the output parameter for the Q-switched laser in active method
Full size table

4 Comparing the high-power BGBs in active and passive methods

Table 4 Comparing the experimental data on active and passive arrangements
Full size table

In the final step, the passive method is compared to the active method reported in Sect. 3.3. For this purpose, high-power laser of CW-BGBs are set up using the passive method. All the characteristics of the laser cavity and optical elements are the same as those described in Sect. 3.3. The transverse mode of BGBs generated in the passive arrangement basically depends on the angular momentum order of Laguerre–Gaussian beams [33]. Table 4 shows the experimental results of the active and passive methods for the CW laser. According to it, the active method is more efficient than the passive method. For example, the output efficiencies of the zero-order laser are \(26\%\) and \(6.5\%\) for the active and passive arrangements, respectively. It is difficult and time-consuming to reach high-order modes in the passive regime especially for high-power lasers.

5 Discussion

In this section, some important results generally are discussed as follows:

  1. 1.

    The comparison of the selective mode of Bessel–Gaussian and Gaussian beams, which have significant difference, can be apprehensive. Working with Gaussian beams shows that decreasing the radius of the aperture leads to the reduction of the mode orders. Therefore, the fundamental mode of Gaussian beams (zero order) is obtained at the lowest radius of the aperture in despite of the achieved results in BGBs.

  2. 2.

    The ring shape of BGBs also can be obtained with propagating fundamental mode (\(J_0\)) called far field. Some limiting conditions in designing high-power and high-order lasers play a role in the radius of ring-shaped lasers (order of modes) and their nature (far-field or high-order BGBs). To gain more comprehension the nature of produced ring shapes in the resonator, just an example of such modes of the HOTM of CW-BGBs (highest possible mode \(J_{10}\)) with simulation result of the far field of fundamental mode is drawn a good comparison in Fig. 6. It is clear that the shape of the fundamental far field do not match neither the experimental nor the theoretical of high-order mode \(J_{10}\). It is clear that round trips of ring-shaped beams with the radius of about > 2 mm are impossible in this setup. Therefore, the HOTMs of BGBs should not be confused with the far fields, because the radius of the ring beams in the far field of the basic mode is at least 2.5 mm.

  3. 3.

    According to Ref. [24], in practice, all Gaussian beams cannot be perfectly transformed to BGBs, whereas, in simulating the BGBs, this transformation can be absolutely and thoroughly performed. This difference emerges as low-intensity peaks middle of the high-order modes of BGBs rings. It should be noted that this deviation depends on some parameters such as the quality of the axicon prism, the optical element of the resonator, and the design of the laser.

  4. 4.

    Due to the importance and applications of the main ring in HOTM especially in high-power lasers, the main ring mostly is considered in transverse modes; thus, amplifying and oscillating of the side rings were prevented by employing aperture “b”. Consequently, the number of the output side rings is limited and this leads to increase medium gain, better beam quality, and high intensity of the main ring.

Fig. 6
figure 6

The theoretical far field of the fundamental mode (\(J_0\)) of BGB from the output mirror in the optical length of four round trip \(=800\) mm (dashed-dot-blue line) together with the theoretical and the experimental of HOTM of BGB (\(J_{10}\)) using the aperture radius “a” of \(r_{{\text {a}}} =0.7\) mm in the CW laser (solid-black and dot-red lines)

Full size image

6 Conclusion

In this paper, the selective transverse modes of high-power Bessel–Gaussian lasers were generated by axicon-based resonators (active method) in pulsed/CW regimes. Two distinct features of this study can be pointed out. First, the transverse mode can be selected appropriately just by optimizing the resonator length in the absence of an aperture. Second, the HOTMs of BGBs are directly selected by tuning the radius of the aperture “a” close to the plane mirror-axicon without changing other resonator parameters. It was demonstrated that the mode selection in active resonators highly depends on the limiting propagation factors such as the radius and location of apertures and the optical length of the resonator. Comparing the experimental results with their corresponding simulations strongly confirm that the selected high-power modes are actually higher order modes of BGBs. It should be noted that round-trips of ring-shaped beams with the radius of about > 2 mm are impossible. Therefore, the HOTMs of BGBs should not be confused with the far fields of fundamental mode. At last, a passive resonator was also set up and results were compared with the active one. The comparison shows that in the passive arrangement, the output power efficiency was lower than that of the active arrangement and higher order transverse modes were hardly achievable. Therefore, the active resonator is highly advised for high-power regimes due to its reliability, ease of use, and simple recognition of the selected higher order modes.