Molecular relaxation effects on vibrational water vapor photoacoustic spectroscopy in air

Abstract

Photoacoustic spectroscopy is a highly sensitive technique, well suited for and used in applications targeting the accurate measurement of water vapor in a wide range of concentrations. This work demonstrates the nonlinear photoacoustic response obtained for water vapor in air at typical atmospheric concentration levels, which is a result of the resonant vibrational coupling of water and oxygen. Relevant processes in the relaxation path of water in a mixture with air, excited with near-infrared radiation, are identified and a physical model for the acoustic signal measured with a resonant photoacoustic cell is presented. The model is valid for modulation frequencies typical for conventional and quartz-enhanced photoacoustic spectroscopy and provides a simplified means of calibration for photoacoustic water vapor sensors. Estimated values for comprised model coefficients are evaluated from photoacoustic measurements of water vapor in synthetic air. Furthermore, it is shown experimentally that the process of vibrational excitation of nitrogen is of negligible importance in the relaxation path of water vapor and thus insignificant in the photoacoustic heat production in atmospheric measurement environments.

1 Introduction

The amount of published research on photoacoustic spectroscopy and the number of commercially available sensor systems based on this method are rising steadily, as technical advances allowed substantial progress in the limits of detection (LOD) and reduction of size and cost (e.g., [1, 2]). While the technical advances lead to increased sensitivities and allow for detection at trace levels, the upper limits remain more or less unaltered, yielding increased dynamic ranges of the methods.

Water vapor in atmospheric measurement environments can vary over a wide range of concentrations, which therefore makes photoacoustic (PA) spectroscopy an ideal detection and measurement technique. Water vapor mole fractions can fall below 10 ppm in the upper troposphere as well as lower stratosphere, and rise above 40,000 ppm for dew points around 30 °C at standard pressure [3]. A large number of applications for the PA measurement of water vapor already exists, mostly measuring at wavelengths in the near infrared [4,5,6,7,8,9,10,11,12,13,14]. In the overwhelming majority of literature, the measured PA signal is interpreted in terms of a linear response. Quite often, validation or calibration measurements are conducted for a narrow range of concentrations and the response is linearly extrapolated to lower or higher concentrations. Linear extrapolation is also used for the determination of the LOD. In the case of an incorrect linear assumption, extrapolation inevitably leads to large errors in the predicted concentrations and also in the predicted theoretical LOD.

Tátrai et al. [11] have calibrated a photoacoustic hygrometer for a large range of water vapor concentrations and determined a nonlinear relationship between the measured microphone response and the water vapor mixing ratio. A tenth-order polynomial fit had to be applied to calibrate the device. High absorption and a resulting nonlinear power loss, given by the Beer–Lambert law, explain sensitivity losses at high concentrations, and it is also known that a background signal not or incorrectly subtracted can cause a nonlinear behavior at low concentrations [15]. These effects, however, do not explain pronounced increases in sensitivity at intermediate concentrations as observed by Tátrai et al. and which are also reproduced in this work. Other drawbacks of using polynomial functions of high order are the generally poor results achieved for extrapolations of the PA signal to concentrations outside of the calibration range.

Nonlinear relationships between PA response and concentration have previously been reported when molecular relaxation times of molecules involved in the relaxation path are comparable to the time variation of the incident radiation and relaxation times change with varying concentration. Several well-known practical examples of combinations of absorbing species and buffer gases exist, where the overall relaxation time is in the order of the modulation period. For example, the first vibrationally excited, asymmetric stretching mode of carbon dioxide, ${{\rm CO}_2}$(0,0,1) ($2349\ \,{\rm cm}^{-1}$), is long known to exhibit a near-resonant, vibrational–vibrational (V–V) coupling with ${\rm N}_{2}$, which leads to a long relaxation time at atmospheric conditions, due to the long lifetime of the first excited state of the nitrogen molecule, ${\rm N}_{2}$(1) ($2331\ \,{\rm cm}^{-1}$) [16]. Another example for near-resonant coupling of practical relevance is known to exist between the bending modes of methane ($1311\ \,{\rm cm}^{-1}$ and $1533\ \,{\rm cm}^{-1}$) and vibrationally excited molecular oxygen, as ${\rm O}_{2}$(1) ($1556\ \,{\rm cm}^{-1}$) again has a long lifetime [17].

Water vapor is utilized as a highly efficient promoter for vibrational–translational (V–T or thermal) collisional relaxation [18], also acting as a promoter in the V–T relaxation of ${\rm O}_{2}$(1) [17]. Water is either added to maximize the photoacoustic response [4, 17, 19], or measured simultaneously, to correct for changing overall relaxation times [5]. However, the ${\rm H}_{2}{\rm O}$ molecule itself has a near-resonant V–V coupling of the first bending mode, ${\rm H}_{2}{\rm O}$($\nu _1\,{=}\,0$, $\nu _2\,{=}\,1$, $\nu _3\,{=}\,0$) ($1595\ \,{\rm cm}^{-1}$), with ${\rm O}_{2}$(1), with an energy transfer more efficient than the thermal relaxation by the major atmospheric constituents ${\rm O}_{2}$ and ${\rm N}_{2}$ [20, 21]. This suggests a corresponding PA signal loss, when measuring water vapor at low concentrations in atmospheric environments at typical modulation frequencies and when the relaxation path involves the ${\rm H}_{2}{\rm O}$(0,1,0) state. Combined with the properties of ${\rm H}_{2}{\rm O}$ as an efficient promoter of V–T relaxations at increasing concentrations, a variable relaxation time and hence a nonlinear PA response when measuring water vapor in air are to be expected.

In this work, a simplified model of the relaxation process of water vapor in atmospheric environments, applicable to vibrational photoacoustic spectroscopy, is postulated and validated experimentally. Model parameters derived from relaxation rates and setup parameters are evaluated from photoacoustic measurements of water vapor at varying concentrations in air by comparison of the predicted PA amplitude and phase shifts with the experimentally measured amplitude and phase. Measurements of the PA response of water vapor in a nitrogen-buffered environment are presented to affirm assumptions about the relaxation process. Finally, a simplified model of the photoacoustic response, valid for modulation frequencies typical for conventional and quartz-enhanced photoacoustic spectroscopy, is provided as a means of calibrating PA water vapor sensors.

2 Theory

2.1 Linear photoacoustic response

The often applied theoretical result of a linear dependence of the background-corrected photoacoustic signal amplitude (at the frequency of modulation), S (in V), on the number concentration of a single absorbing gas species, $n_g$ (in ${\rm molecules}/{\rm m}^3$), is given by [1]

$$\begin{aligned} S = C_{\rm cell}\, \sigma \, P\, n_g\, \eta , \end{aligned}$$

(1)

with average radiation power P (in W), cell constant $C_{\rm cell}$ (including microphone sensitivity, in Vm/W), absorption cross section $\sigma$ (in ${\rm m}^2/{\rm molecule}$) and efficiency of conversion of the radiation into heat $\eta$. This expression assumes negligible power loss along the optical path and absorption cross sections and applied intensities also have to be low to prevent significant depletion of the ground state of the targeted transition [22]. This conditions are fulfilled for most near-infrared laser photoacoustic sensor applications, as absorbance usually is sufficiently low and mostly diode lasers with powers up to only several tens of milliwatts are applied. For water vapor at high concentrations and typical absorption path lengths, however, significant absorbance has to be expected.

In addition to the above assumptions, the energy-weighted, average vibrational relaxation time from the excited vibrational state back to the initial state, $\tau$, is usually assumed shorter than the time variation of the incident radiation ($\omega \tau \ll 1$, with the angular frequency of modulation $\omega = 2 \pi f$) [22]. Therefore, the photoacoustic conversion efficiency,

$$\begin{aligned} \eta = \frac{1}{\sqrt{1+(\omega \tau )^2}}, \end{aligned}$$

(2)

is implicitly assumed to be unity, which results in a linear PA response. A linear behavior may also be observed when the condition $\omega \tau \ll 1$ is not fulfilled. The relaxation time may be in the order of the modulation period or longer, but constant for a given combination of absorbing species and buffer gas. The signal amplitude given by Eq. (1) then still is a linear function of the concentration.

Currently, no assessment of the conversion efficiency for PA measurements of water vapor in air exists. For this reason, the photoacoustic conversion efficiency is investigated theoretically and experimentally in the following. Conversion efficiencies different from unity are only measurable in the amplitude of the PA signal by varying the modulation frequency, gas temperature or pressure, while correcting for a change in microphone sensitivity and frequency response, radiation waveform and corresponding dependencies of the cell constant. Otherwise, deviations from an efficiency of unity are indiscernible from a changing cell constant. However, it is often overlooked that the phase shift, $\phi$, of the PA response, which is not only a function of the average lifetime of the excited vibrational state, but may be a complicated function of a number of different relaxation times of states involved in the relaxation process, contains valuable information about the relaxation time and thus also the conversion efficiency, as

$$\begin{aligned} \phi =\arctan {(\omega \tau )} \end{aligned}$$

(3)

[23]. This relationship is used in the present work to experimentally verify the PA response and conversion efficiency for water vapor in air derived in the following.

2.2 Model for the photoacoustic response of water vapor in air

The near-infrared is also favored in most PA water vapor sensing applications, due to the high absorption line strengths and the availability of relatively cheap distributed feedback laser diodes in this region. Mainly, ro-vibrational transitions from the vibrational ground state ${\rm H}_{2}{\rm O}$($\nu _1\,{=}\,0$,  $\nu _2\,{=}\,0$,  $\nu _3\,{=}\,0$), to the vibrational ${\rm H}_{2}{\rm O}$(1,0,1) ($7250\ \,{\rm cm}^{-1}$) state of the main ${\rm H}_{2}{\rm O}$ isotope are targeted, where the variables $\nu _1$, $\nu _2$ and $\nu _3$ denote the state of the symmetric stretch, bending, and asymmetric stretch vibrational mode, respectively. For this reason, the following derivation addresses relaxation from the vibrational ${\rm H}_{2}{\rm O}$(1,0,1) state. However, as will be shown below, the relaxation path can be approximated by a three-level system of the ${\rm H}_{2}{\rm O}$($\nu _1$, $\nu _2$, $\nu _3$), ${\rm H}_{2}{\rm O}$($\nu _1$, $\nu _2{-}1$, $\nu _3$), ${\rm O}_{2}$(1) and ${\rm O}_{2}$(0) levels, which reduces the complexity of the relaxation process. This implies that the model should extend to situations where lower vibrational states are excited by radiation and may also be applicable at higher excitation energies.

At typical PA measurement temperatures and pressures, rotational relaxation rates are much higher than typical modulation frequencies, so that the rotational temperature can be assumed equal to the translational temperature of the gas for all steps in the relaxation path [32]. For this reason, only relaxation of vibrationally excited levels needs to be considered. Nevertheless, to accurately model the relaxation process from the excited ${\rm H}_{2}{\rm O}$(1,0,1) level in air, one would need to model at least 13 ${\rm H}_{2}{\rm O}$ vibrational energy levels, as well as 2 levels each for the main constituents ${\rm O}_{2}$ and ${\rm N}_{2}$ (e.g., [24, 33]) and all possible reactions among the participating molecular levels (cf. Fig. 1). Although relaxation through and by trace constituents may occur in atmospheric environments (mainly Ar and ${{\rm CO}_2}$), only reactions between water, molecular oxygen and nitrogen are considered in the following kinetic analysis. The possible consequences of this restriction are discussed in the supplementary material, Sec. S1. Relevant relaxation reactions and literature values for the corresponding reaction rate coefficients with references are given in Table 1.

Fig. 1

Energy diagram of the vibrational levels of the considered constituents. ${\rm H}_{2}{\rm O}$ levels considered in reservoirs are connected by gray rectangular boxes. The radiative excitation is indicated by a wavy line

Table 1 Main processes of vibrational energy exchange of ${\rm H}_{2}{\rm O}$ in atmospheric environments. ${\rm M}$ is either ${\rm O}_{2}$ or ${\rm N}_{2}$. T is the temperature in Kelvin and $T_r$ the reference temperature of 300 K. Values for the rate coefficients have to be taken with care, as uncertainties and discrepancies between measured rates are generally high

As modeling the full system is impractical, it is shown in the following sections that the system can be approximated by the three-level system, describing the rate-determining steps of the relaxation process and the heat released in dependence of the gas composition. The assumptions leading to the three-level model are discussed in the next section by reference to the relaxation processes in Table 1. Typical time constants for these reactions in air at $35\,^{\circ }\hbox {C}$, 800 hPa and different water vapor concentrations are given in Fig. 2. Time constants are calculated from $\tau =1/{\rm k}[{\rm B}]$, where $[{\rm B}]$ is the concentration of the second reactant, which is assumed to remain constant. For brevity, molecules excited to the lowest vibrational level above the ground level are denoted by an asterisk in the following (e.g., ${{\rm O}_2^*}$ instead of ${\rm O}_2$(1)). ${\rm M}$ denotes either ${\rm O}_{2}$ or ${\rm N}_{2}$. Relaxation processes are denoted by (Ri), with the reaction number i given in Table 1.

Fig. 2

Approximate time constants for reactions in Table 1 with $\nu _2\,{=}\,1$ at $35\,^{\circ }\hbox {C}$ and 800 hPa in air together with typical PA modulation periods (frequencies of 1 kHz to 33 kHz). Time constants of (R7), (R13) and (R14) are indicated for ${\rm H}_2{\rm O}$ mole fractions of 100 ppm (dashed arrow) and 20,000 ppm (solid arrow). Values for time constants of reactions (R1) and (R4) are smaller, (R12) larger than the drawn scale

2.2.1 Assessment of relaxation path

The low energy differences between the pairs of ${\rm H}_{2}{\rm O}$ levels $(1,0,1) \leftrightarrow (2,0,0)$, $(1,2,0) \leftrightarrow (0,2,1)$, $(1,1,0) \leftrightarrow (0,1,1)$ and $(1,0,0) \leftrightarrow (0,1,1)$ is the reason for the fast relaxation rate coefficient of ${\rm k}_1^{V{-}V}$ and ${\rm k}_4^{V{-}V}$ in reactions (R1) and (R4) (in both directions). So after initial excitation into the ${\rm H}_{2}{\rm O}$(1,0,1) state and after further steps in the relaxation process, this leads to a fast and efficient equilibration of the corresponding level pairs. As a result, each pair can be viewed as a single reservoir [24, 34, 35].

From these reservoirs $\nu _1$ and $\nu _3,$ stretching quanta are quickly converted to two $\nu _2$ quanta via processes (R2), (R3), (R5) and (R6). The energies released by these transitions of ${\rm H}_{2}{\rm O}$ and of the above reactions, (R1) and (R4), are considered to be transferred to kinetic energy instantaneously. Justifications of this assumption are the high relaxation rates and short corresponding lifetimes of these reactions near atmospheric conditions ($\tau \,{=}\,1/({\rm k}[{\rm M}])\le \,{1}\,\upmu {\rm s}$; cf. Fig. 2) in comparison to conventional and also quartz-enhanced PA spectroscopy (QEPAS, modulation frequencies typically up to 33 kHz).

It is difficult to evaluate theoretically if the vibrational excitation of ${\rm N}_{2}$ plays a role in the reduction of the PA signal at low concentrations of ${\rm H}_{2}{\rm O}$. A similar relaxation delay as with oxygen can be expected when nitrogen is vibrationally excited in relevant numbers, since the lifetime of ${{\rm N}_2^*}$ in air is even longer than that of ${{\rm O}_2^*}$ (see (R12)). The large energy difference of $736\ \,{\rm cm}^{-1}$ between the levels of ${\rm H}_{2}{\rm O}$ and ${{\rm N}_2^*}$ in the V–V process (R10) makes this process unlikely, which is why it has mainly been measured in the backward sense, with various values collected by Whitson et al. [28]. However, Feofilov et al. [33] cite a forward reaction rate, repeated in Table 1, in the same order as the backward rate from Whitson et al., possibly calculated by the principle of detailed balance. This relaxation process would compete with reactions (R7), (R8) and (R9). The rate of reaction (R15) suggests that the coupling of the vibrationally excited ${\rm N}_{2}$ and ${\rm O}_{2}$ levels and excitation of ${\rm N}_{2}$ through this process can be neglected. Therefore, ${{\rm N}_2^*}$ and ${{\rm O}_2^*}$ populations can be studied independently and the effect of excitation of nitrogen can be experimentally measured by measuring the PA response at varying ${\rm H}_{2}{\rm O}$ fractions in a purely nitrogen-buffered environment. Measurement results at the modulation frequency of 4.6 kHz for such an environment proving negligible excitation of ${\rm N}_{2}$ are presented in Sect. 4.1.

At low fractions of water in air, the most probable relaxation process from the levels ${\rm H}_{2}{\rm O}$($\nu _1$,$\nu _2{\ne }0$,$\nu _3$), which includes in total six ${\rm H}_{2}{\rm O}$ levels, is the V–V transfer to ${{\rm O}_2^*}$ (R9). This process is much faster than typical PA modulation periods ( $1/\left\{ {\rm k}_9^{V{-}V}[{{\rm O}_2}]\right\} \le \,{1}\,\upmu {\rm s}$; cf. Fig. 2). As the sequential conversion of up to all four $\nu _2$ quanta is still fast in comparison to one PA modulation period, it is possible to regard each ${\rm H}_{2}{\rm O}$($\nu _1$,$\nu _2{\ne }0$,$\nu _3$) molecule as $\nu _2$ molecules in a reservoir with $\nu _2=1$ and an average lifetime of $\tau _{{\rm H}_2{\rm O}^*}$. ${{\rm H}_2{\rm O}^*}$ denotes this single reservoir. Increasing water vapor fractions lead to a competing relaxation of molecules in the reservoir by collision with ${\rm H}_{2}{\rm O}$ (R7). As mentioned in the introduction, this process is even more efficient than the coupling to ${\rm O}_{2}$, only decreasing the relaxation time of the reservoir. Hence, on the timescale of the modulation period, there is negligible difference in considering the total number of available $\nu _2$ quanta instead of the number of excited ${\rm H}_{2}{\rm O}$ molecules at a given point in time. The viewpoint of a single reservoir, ${{\rm H}_2{\rm O}^*}$, with an equivalent number of excited molecules with $\nu _2=1$, thus can be maintained from low to high water vapor mole fractions.

Taken together, the overall rate of relaxation of ${\rm H}_{2}{\rm O}$(1,0,1) in air is mainly determined by the following competing relaxation processes, for which the relaxation path is schematically drawn in Fig. 3:

• 1. V–T relaxation of the bending mode of ${\rm H}_{2}{\rm O}$($\nu _1$,$\nu _2\;{\ne }\;0$,$\nu _3$) by one through collisions with ${\rm O}_{2}$, ${\rm N}_{2}$ or ${\rm H}_{2}{\rm O}$, i.e., processes (R7) and (R8).

• 2. V–V energy transfer to ${\rm O}_{2}$, with relaxation of the bending mode of ${\rm H}_{2}{\rm O}$($\nu _1$,$\nu _2\;{\ne }\;0$,$\nu _3$) by one and excitation of ${\rm O}_{2}$ to ${{\rm O}_2^*}$, i.e., process (R9).

• 3. V–T relaxation of ${{\rm O}_2^*}$ to the ground state, through collisions with ${\rm O}_{2}$, ${\rm N}_{2}$ or ${\rm H}_{2}{\rm O}$, i.e., processes (R11) and (R13).

Fig. 3

Relaxation path diagram for the relaxation from the ${{\rm H}_2{\rm O}^*}$ reservoir. Arrow widths are scaled with the magnitude of the labeled pseudo-first-order reaction rates, calculated for a 100 ppm and b 20,000 ppm water vapor mole fraction in air. Paths drawn with dashed arrows indicate rates much lower than can be indicated on the chosen scale

In the following analysis of the relaxation path, the forward rate coefficients of the total five involved reactions have been renamed for easier identification. The rate coefficient symbols used in the model and the corresponding reactions are given in Table 1. Subscripts of the rates have been renamed according to the initial reactants. Superscripts of these rates again specify whether the reaction is of V–T or V–V type.

2.2.2 Three-level relaxation model

The above five remaining processes can be described by a simplified three-level model, similar to the one described by Hunter [36], drawn schematically in Fig. 4.

Fig. 4

Energy and relaxation path diagram for the proposed three-level model, describing the relaxation from the ${{\rm H}_2{\rm O}^*}$ reservoir with coupling to the first vibrationally excited state of ${\rm O}_{2}$. Energies of the ${\rm H}_{2}{\rm O}$ ground state and the ${\rm H}_{2}{\rm O}$(1,0,1) level are not to scale

This system is described by the rates of change of the number concentrations of vibrationally excited water molecules in the reservoir, $[{{\rm H}_2{\rm O}^*}]$, and vibrationally singly excited molecular oxygen, $[{{\rm O}_2^*}]$:

$$\begin{aligned} \frac{{\rm d} [{{\rm H}_2{\rm O}^*}]}{{\rm d}t}&= 4 \sigma \varphi ({\mathbf {r}},t) [{\rm H}_2{\rm O}] - \frac{[{{\rm H}_2{\rm O}^*}]}{\tau _{{\rm H}_2{\rm O}^*}}, \end{aligned}$$

(4)

$$\begin{aligned} \frac{{\rm d} [{{\rm O}_2^*}]}{{\rm d}t}&= k_{{{\rm O}_2^*}}^{{\rm H}_2{\rm O}^*} [{{\rm H}_2{\rm O}^*}] - \frac{[{{\rm O}_2^*}]}{\tau _{{{\rm O}_2^*}}}. \end{aligned}$$

(5)

The first term on the right hand side of Eq. (4) describes the excitation of water molecules from the ground state, by absorption of photons with energy $h \nu$, in a radiation photon flux, $\varphi (t)$, harmonically modulated at the angular frequency $\omega$:

$$\begin{aligned} \varphi ({\mathbf {r}},t) = \frac{I({\mathbf {r}})}{h \nu } (a + b\,{\rm e}^{i\omega t}). \end{aligned}$$

(6)

$I({\mathbf {r}})$, a and b describe the irradiance at position $\mathbf {r}$. $\sigma$ is the absorption cross section of ${\rm H}_{2}{\rm O}$ at the radiation frequency $\nu$, also depending on gas composition, pressure and temperature. A prefactor of 4 is included to describe the conversion of the radiatively excited ${\rm H}_{2}{\rm O}$(1,0,1) to four vibrationally excited molecules in the reservoir ${{\rm H}_2{\rm O}^*}$. The second term gives the combined de-excitation rate by V–T relaxation to the ground state and the resonant V–V transfer to ${{\rm O}_2^*}$, described by the ${\rm H}_2{\rm O}$-concentration dependent, average lifetime of the ${{\rm H}_2{\rm O}^*}$ state, $\tau _{{\rm H}_2{\rm O}^*}$. It is implicitly assumed that the number of excited molecules is small in comparison to the number of molecules in the ground state, hence $[{\rm H}_2{\rm O}]$ can be assumed constant and stimulated emission can be neglected.

The ${{\rm O}_2^*}$ level is populated by the aforementioned V–V energy transfer and relaxes to the ground state after an ${\rm H}_2{\rm O}$-concentration dependent average lifetime $\tau _{{{\rm O}_2^*}}$. The italicized letter k is used for average pseudo-first-order reaction rate coefficients, with superscripts and subscripts specifying initial and final states in the relaxation path, respectively. Inverse average lifetimes of the excited states are given by

$$\begin{aligned} \tau _{{\rm H}_2{\rm O}^*}^{-1}&= k^{{\rm H}_2{\rm O}^*}_{0}+ k_{{{\rm O}_2^*}}^{{\rm H}_2{\rm O}^*}\nonumber \\&= {\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V-T}[{\rm M}]+ {\rm k}_{{{\rm H}_2{\rm O}^*},{\rm H}_2{\rm O}}^{V-T}[{\rm H}_2{\rm O}]\nonumber \\&\quad + {\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V-V}[{{\rm O}_2}]\end{aligned}$$

(7)

$$\begin{aligned} \tau _{{{\rm O}_2^*}}^{-1}&= k^{{{\rm O}_2^*}}_{0}= {\rm k}_{{{\rm O}_2^*},{\rm M}}^{V-T}[{\rm M}]+ {\rm k}_{{{\rm O}_2^*},{\rm H}_2{\rm O}}^{V-T}[{\rm H}_2{\rm O}]\ , \end{aligned}$$

(8)

where as above, the roman type k is used for second-order reaction rate coefficients. $[{\rm M}]$ stands for the sum of ${\rm O}_{2}$ and ${\rm N}_{2}$ concentrations, and the associated collisional relaxation rates, ${\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V{-}T}$ and ${\rm k}_{{{\rm O}_2^*},{\rm M}}^{V{-}T}$, are weighted averages for the two constituents.

As summed up in the previous section, $\tau _{{\rm H}_2{\rm O}^*}$ is governed by processes (R7), (R8) and (R9), and $\tau _{{{\rm O}_2^*}}$ by processes (R11) and (R13). In accordance with Hunter [36], the solutions to the system of Eqs. (4)-(5) are given by

$$\begin{aligned}{}[{{\rm H}_2{\rm O}^*}]&= \frac{4 \sigma b I}{h \nu } \frac{\tau _{{\rm H}_2{\rm O}^*} [{\rm H}_2{\rm O}]\ {\rm e}^{i(\omega t - \phi _{{\rm H}_2{\rm O}^*})}}{\sqrt{1+\omega ^2\tau _{{\rm H}_2{\rm O}^*}^2}}, \end{aligned}$$

(9)

$$\begin{aligned}{}[{{\rm O}_2^*}] =&\frac{4 \sigma b I}{h \nu } \frac{\tau _{{\rm H}_2{\rm O}^*}\ \tau _{{{\rm O}_2^*}}\ k_{{{\rm O}_2^*}}^{{\rm H}_2{\rm O}^*}\ [{\rm H}_2{\rm O}]\ {\rm e}^{i(\omega t - \phi _{{\rm H}_2{\rm O}^*} - \phi _{{{\rm O}_2^*}})}}{\sqrt{1+\omega ^2\tau _{{\rm H}_2{\rm O}^*}^2}\sqrt{1+\omega ^2\tau _{{{\rm O}_2^*}}^2}}\ , \end{aligned}$$

(10)

where explicit spatial and temporal dependencies have been omitted for brevity. Constant terms and terms with decaying factors $\exp {(-t/\tau _{{\rm H}_2{\rm O}^*})}$ and $\exp {(-t/\tau _{{{\rm O}_2^*}})}$ have been neglected, as they do not contribute to the resonant photoacoustic signal after a few multiples of the relaxation times. The phase delay of the signals is given by

$$\begin{aligned} \tan {(\phi _{{\rm H}_2{\rm O}^*})}&= {\omega }\,\tau _{{\rm H}_2{\rm O}^*}, \end{aligned}$$

(11)

$$\begin{aligned} \tan {(\phi _{{{\rm O}_2^*}})}&= \frac{\omega \left( \tau _{{{\rm O}_2^*}}+ \tau _{{\rm H}_2{\rm O}^*}\right) }{1-\omega ^2\tau _{{{\rm O}_2^*}}\tau _{{\rm H}_2{\rm O}^*}} \approx {\omega }\,\tau _{{{\rm O}_2^*}}, \end{aligned}$$

(12)

where the last approximation holds because of the short lifetime of the ${{\rm H}_2{\rm O}^*}$ reservoir.

2.2.3 Photoacoustic heat source rate

The photoacoustic source rate of heat production per unit volume and time is then given by the sum of heat released by the three transitions drawn in Fig. 4 and the heat assumed to be released instantaneously after excitation by rotational relaxation and the conversion of $\nu _1$ and $\nu _3$ to $\nu _2$ quanta, i.e., reactions (R1) to (R6):

$$\begin{aligned} {\mathbf {H}}({\mathbf {r}},t)&= \Big (k_{0}^{{\rm H}_2{\rm O}^*} E_{{\rm H}_2{\rm O}^*} + k_{{{\rm O}_2^*}}^{{\rm H}_2{\rm O}^*} \left( E_{{\rm H}_2{\rm O}^*} {-} E_{{{\rm O}_2^*}}\right) \Big )[{{\rm H}_2{\rm O}^*}] \nonumber \\&\quad + k^{{{\rm O}_2^*}}_{0}E_{{\rm O}_2^*}[{{\rm O}_2^*}] + \sigma \varphi (t) E_{{\rm inst}}[{\rm H}_2{\rm O}]. \end{aligned}$$

(13)

Here, $E_{{\rm inst}}$ is the average energy per excited molecule, released by the mentioned rotational relaxation and the vibrational conversion. Since the energies of the ${\rm O}_{2}$(1) level and the ${{\rm H}_2{\rm O}^*}$ reservoir are approximately equal ($-89\,{\rm cm}^{-1}$ to ${19}{\,{\rm cm}^{-1}}$ difference for $\nu _2=\{1,2,3,4\}$), we can set

$$\begin{aligned} E_{{\rm H}_2{\rm O}^*}&= E_{{{\rm O}_2^*}}, \end{aligned}$$

(14)

without greater losses in the energy balance. With the literature values for the relevant relaxation rate coefficients stated in Table 1, the following approximations are used in finding a simplified solution for the photoacoustic response as a function of the ${\rm H}_{2}{\rm O}$ concentration:

$$\begin{aligned} {\rm k}_{{{\rm O}_2^*},{\rm M}}^{V-T}[{\rm M}]\ll {\omega } \ll {\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V-V}[{{\rm O}_2}]. \end{aligned}$$

(15)

The left-hand-side of Eq. (15) results in the model being independent of reaction (R11), which is reasonable considering the low rate coefficient.

Writing the photoacoustic source rate in a form with harmonic time dependence,

$${\mathbf {H}}({\mathbf {r}},t) = {\boldsymbol{\mathcal{H}}}\left( {\mathbf {r}},\omega \right) \cdot {\rm e}^{i\omega t},$$

(16)

and using the assumptions of Eq. (15) together with the solutions for $[{{\rm H}_2{\rm O}^*}]$ and $[{{\rm O}_2^*}]$ (Eqs. (9) and (10)) in the equation for the time-dependent photoacoustic source rate, Eq. (13), the complex amplitude at the frequency of modulation can be written as a function of the mole fraction of water, $x_{{\rm H}_2{\rm O}}$ (see supplementary material):

$${\boldsymbol{\mathcal{H}}}\left( {\mathbf {r}},\omega \right) \approx \sigma \,b\,I\,n_0\, x_{{\rm H}_2{\rm O}}\,{\varvec{\eta }}(x_{{\rm H}_2{\rm O}}) ,$$

(17)

with

$$\begin{aligned} {\varvec{\eta }}(x_{{\rm H}_2{\rm O}})&= \frac{1}{c_1 + x_{{\rm H}_2{\rm O}}+ c_2 \left( 1-x_{{\rm H}_2{\rm O}}\right) } \cdot \left(\vphantom {\left. + \frac{c_2 \left( 1-x_{{\rm H}_2{\rm O}}\right) \,{\rm e}^{-i \arctan {\left( \frac{\omega }{c_3\,n_0\,x_{{\rm H}_2{\rm O}}} \right) }}}{\sqrt{1+\omega ^2/\left( c_3\,n_0\,x_{{\rm H}_2{\rm O}}\right) ^2}}\right) }c_1 + x_{{\rm H}_2{\rm O}}\right. \nonumber \\&\quad \left. + \frac{c_2 \left( 1-x_{{\rm H}_2{\rm O}}\right) \,{\rm e}^{-i \arctan {\left( \frac{\omega }{c_3\,n_0\,x_{{\rm H}_2{\rm O}}} \right) }}}{\sqrt{1+\omega ^2/\left( c_3\,n_0\,x_{{\rm H}_2{\rm O}}\right) ^2}}\right) \ , \end{aligned}$$

(18)

where

$$\begin{aligned} c_1&= \frac{{\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V{-}T}+\frac{E_{{\rm inst}}}{h\,\nu }\,{\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V{-}V}\, x_{{{\rm O}_2},\mathrm {{dry}}}}{{\rm k}_{{{\rm H}_2{\rm O}^*},{\rm H}_2{\rm O}}^{V{-}T} - {\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V{-}T}-\frac{E_{\mathrm{inst}}}{h\,\nu }\,{\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V{-}V}\,x_{{{\rm O}_2},\mathrm {{dry}}}}, \end{aligned}$$

(19)

$$\begin{aligned} c_2&= \frac{\frac{4E_{{\rm H}_2{\rm O}^*}}{h\,\nu }\,{\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V{-}V}\,x_{{{\rm O}_2},\mathrm {{dry}}}}{{\rm k}_{{{\rm H}_2{\rm O}^*},{\rm H}_2{\rm O}}^{V{-}T} - {\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V{-}T}-\frac{E_{\mathrm{inst}}}{h\,\nu }\,{\rm k}_{{{\rm H}_2{\rm O}^*},{{\rm O}_2}}^{V{-}V}\,x_{{{\rm O}_2},\mathrm {{dry}}}}, \end{aligned}$$

(20)

$$\begin{aligned} c_3&= {\rm k}^{V{-}T}_{{\mathrm{O}}_2^*},{\rm{H}}_2{\rm{O}} . \end{aligned}$$

(21)

Here, $n_0$ (in $\hbox {molecules/m}^{3}$) is the overall number concentration or density at the measurement temperature, T, and pressure, p, calculated for an ideal gas in the remainder of this work. Slight improvements in the prediction of the PA response should be possible, when also considering the real gas effects. $x_{{{\rm O}_2},\mathrm {{dry}}}$ is the molecular oxygen mole fraction in dry air. Finally, the absolute value of ${\varvec{\eta }}$ is the overall conversion efficiency, $\eta$ (cf. Eq. (1)), which is a measure of the average relaxation time. The conversion efficiency is lower than one, when the relaxation time is in the order or longer than the modulation period. ${\varvec{\eta }}$ also describes the average phase delay of the PA heat source rate relative to the excitation:

$$\phi \left( {x_{{H_{2} O}} } \right) = Arg({\varvec{\eta}}).$$

(22)

By equating Eqs. (3) and (22), the average relaxation time, $\tau$, can be calculated. Explicit dependencies of ${\varvec{\eta }}$ on $n_0$, $x_{{{\rm O}_2},\mathrm {{dry}}}$ and $\omega$ have been dropped for clarity.

The absorption cross section intrinsically depends on the water vapor mole fraction, as the self-broadening of the chosen absorption line will lead to a non-negligible decrease in the absorption cross section with rising water mole fractions. This can either be taken into account by defining $\sigma$ as a function of water mole fraction, or, approximating the absorption cross section with an average, lower value, which is sufficient for the purposes of this work. The introduced parameters $c_1$ to $c_3$ are practically constant in environments with constant dry air mole fractions for ${\rm O}_{2}$ and ${\rm N}_{2}$, which is reasonable for most atmospheric measurement applications.

2.2.4 Microphone signal for a resonant cell

In a resonant PA cell, the complex pressure amplitude, ${\boldsymbol{\mathcal{A}}}_{\mathbf{j}}$, of mode j, at the angular frequency of resonance, $\omega _j$, is proportional to the overlap of the heat source with the complex conjugate of the normal mode of the acoustic resonator, ${\mathbf {p}}_{\mathbf{j}}^{*}$ [22]:

$${\boldsymbol{\mathcal{A}}_j} \propto \int {\mathbf {p}}_j^{*}({\mathbf {r}})\ {\boldsymbol{\mathcal{H}}}({\mathbf {r}},\omega _j)\ {\rm d}V.$$

(23)

Here, the ratio of specific heats was assumed independent of water vapor concentration and the volume integral extends over every point where the integrand does not vanish. Because of the spatial distribution of the (laser) irradiance, a spatial dependence of the rate of heat production remains. As pointed out in the introduction, large absorption at large mole fractions of water vapor will lead to a decrease in sensitivity and in the PA signal generated, due to the decreased irradiance along the beam path. However, for absorptions or path lengths not too large, the Beer–Lambert law and hence the irradiance of a sufficiently collimated laser beam at point l along the PA cell can be approximated linearly by

$$\begin{aligned} I(l,r) = I_0\,g(r)\,(1-\sigma ^\prime \,[{\rm H}_2{\rm O}]\,l), \end{aligned}$$

(24)

with a normalized radial beam profile g(r) and a reduced absorption cross section $\sigma ^\prime$. With the assumptions that the water vapor is uniformly distributed along the laser beam and the acoustic normal mode is symmetric about the center of the cell along the laser beam (as it is the case for the fundamental longitudinal mode in a resonator with open ends), the complex pressure amplitude together with Eqs. (17) and (24) reduces to

$$\begin{aligned} {\boldsymbol{\mathcal{A}}_j}\,\propto \,{\sigma \,P\,n_0\, x_{{\rm H}_2{\rm O}}\,(1{-}\sigma^\prime \,n_0\,x_{{\rm H}_2{\rm O}}\,l_0)} \,{\varvec{\eta }}(x_{{\rm H}_2{\rm O}}), \end{aligned}$$

(25)

where $P=b\,P_0$ is the alternating component radiant flux (i.e., average power). The length $l_0$ is the absorption path length to the center of the resonator. Combining all mentioned and other setup constants affecting the measured signal, including microphone sensitivity, microphone positional dependence and electronic amplification, the complex amplitude of the microphone signal (in V) will be of the form

$$\begin{aligned} {\mathbf {S}}(x_{{\rm H}_2{\rm O}}) = {C_{\rm cell}\,\sigma \,P\,n_0\, x_{{\rm H}_2{\rm O}}\,(1{-}B_{\rm cell}\,n_0\,x_{{\rm H}_2{\rm O}})} \,{\varvec{\eta }}(x_{{\rm H}_2{\rm O}}). \end{aligned}$$

(26)

The introduced cell constants, $C_{\rm cell}$ and $B_{\rm cell}$, will be functions of the variables temperature, pressure and modulation frequency. Thus, determined and stated values for these constants (in the following referred to as ‘setup parameters’) are only valid for a given combination of these variables.

In addition to the explicitly included second-order term in the microphone signal, arising from the linearly approximated laser power attenuation, several more effects will introduce deviations from a linear PA signal. For example, electret condenser microphones as used in this work exhibit a dependency of the microphone sensitivity, $s_{{\rm mic}}$, on humidity, i.e., $s_{{\rm mic}}(T,p,f)\,\,{=}\,\,c_{{\rm mic}}(T,p,f)$${+}\, b_{{\rm mic}}(T,p,f)\, n_0\, x_{{\rm H}_2{\rm O}}$${+}\,{\mathcal {O}}(x_{{\rm H}_2{\rm O}}^2)$, which has to be accounted for [37].

First-order coefficients of these effects in the cell constant $C_{\rm cell}$, such as the microphone humidity sensitivity coefficient $b_{{\rm mic}}$, result in additional second-order terms in the PA signal and thus can be included in the parameter $B_{\rm cell}$, which in the following is referred to as first-order correction of the cell constant (see supplementary material, Sec. S3). The resulting third- and higher-order terms in the microphone signal are neglected.

In the special case, where the microphone sensitivity is independent of humidity and the optical path length is short, the amplitude (absolute value) of the derived theoretical microphone signal reduces to the same form as in Eq. (1).

The resulting function ${\mathbf {S}}(x_{{\rm H}_2{\rm O}})$, describing the amplitude and phase of the generated and measured photoacoustic signal, is a function of the two setup parameters $C_{\rm cell}$ and $B_{\rm cell}$, the three coefficients $c_1$, $c_2$ and $c_3$, the known or measurable values of $\omega _j$, P and $n_0$, and the unknown water vapor mole fraction, $x_{{\rm H}_2{\rm O}}$. When calibration over a large range of water vapor concentrations has to be performed, this function cannot be approximated by a lower degree polynomial, due to the intricate nonlinearity of ${\varvec{\eta }}(x_{{\rm H}_2{\rm O}})$. However, a conventional nonlinear curve fit to measurement data in a limited range can be used to determine the two parameters and three coefficients of ${\mathbf {S}}(x_{{\rm H}_2{\rm O}})$. It can be seen that for a given excitation energy, the parameters $c_1$ to $c_3$ do not depend on the measurement apparatus and thus should be universal for atmospheric measurement applications at similar conditions. A slight temperature dependence should be observable, due to the temperature dependence of the reaction rate coefficients.

In general, it will be advisable to only use the amplitude of the measured PA signal in the curve fit, as at resonance the measurement uncertainty of the amplitude will be much lower than the uncertainty of the measured phase. Additionally, the phase given by the model goes to zero in the limit of small and large mole fractions. In practice, however, some offset of the model phase from the measured phase will be observable, as the measured signal will not reach zero phase, due to time delays in the electronics and signal processing. One possibility to make use of all information available is to include an additional model parameter for the constant phase offset and to include uncertainties for the phase in a nonlinear curve fit of the complex signal.

In most applications, a calibration curve returning the water vapor mole fraction corresponding to a measured PA signal is of interest. Although no closed-form expression for the water vapor mole fraction can be given, $x_{{\rm H}_2{\rm O}}$ can be efficiently determined for a measured PA signal amplitude, $S_i$, by numerically finding the root of $f(x_{{\rm H}_2{\rm O}})=S_i-\Vert {\mathbf {S}}(x_{{\rm H}_2{\rm O}})\Vert$.

3 Experimental setup and methods

To investigate the described effects on the relaxation time of water vapor in air, a single resonant photoacoustic cell is used for measuring the PA amplitude and phase at water vapor mole fractions in the range of 120–22,000 ppm in pure nitrogen and in synthetic air. An overview of the measurement system used for the validation of the relaxation model is shown in Fig. 5. Humidities are set with a humidity generator and further diluted with a gas diluter. In the following, the individual components and methods applied are described in detail.

Fig. 5

Schematic drawing of the experimental setup with zero gas, humidity generator and gas diluter on the left hand side and photoacoustic (PA) cell, together with sampling and conditioning components on the right hand side. Rectangles with p and T mark locations where pressure and temperature, respectively, are controlled within the ranges stated in the text

3.1 Photoacoustic cell

The photoacoustic cell is a custom-built cell designed to handle increased flow rates. A 6 mm diameter cylindrical duct, milled into a stainless steel block, guides the gas flow axially through an acoustic resonator and acoustic filters (see Fig. 6).

Fig. 6

Schematic drawing of the photoacoustic cell and measurement setup. System control and data acquisition are performed on the real-time embedded controller (NI cRIO)

The resonator has a length of 34 mm and is excited at the fundamental longitudinal mode at a frequency around 4580 Hz ($35\,^{\circ }\hbox {C}$) and with the pressure antinode in the middle of the resonator, where a microphone is connected in a noise- and gas-tight enclosure to measure the photoacoustic signal. Acoustically short concentric-tube resonators (SCRs), which are small volume, reactive acoustic bandstop filters similar to quarter-wavelength tubes [38], are connected at both ends of the resonator (i.e., at the pressure nodes). The SCRs are 6 mm in length and have diameters of 34 mm, tuned to the same resonance frequency as the resonator using finite element method based optimization. This maximizes acoustic reflection at the resonator ends for the resonant mode and for unwanted external noise reaching the resonator. To further decrease outside noise transmission at the measurement frequency into the resonator, one additional SCR is placed upstream as well as downstream of the resonance section. The distance between the SCRs is numerically optimized to maximize overall transmission loss. An additional measure to minimize measurement noise is the vibrational decoupling of the cell from the device rack by short sections of PTFE tubing and a vibration absorbing mounting.

The laser source is a fiber-coupled distributed feedback laser diode (NEL, NLK1E5GAAA), temperature controlled to the ${7327.7}\hbox { cm}^{-1}$ (296 K) absorption line, which corresponds to a ro-vibrational transition from the vibrational ground state to the vibrational ${\rm H}_{2}{\rm O}$(1,0,1) state. This specific line was chosen because of the minimal line shift with pressure, high line intensity and low interference from other anticipated atmospheric constituents. The laser is square wave intensity modulated down to just below the lasing threshold at the resonance frequency with a benchtop laser driver (Thorlabs, ITC4001), maintaining an average power of $9.9\pm 0.1\,\hbox {mW}$. The laser beam is collimated to 2 mm diameter, entering and exiting the cell at two flush-mounted N-BK7 Brewster-windows (angle of ${56.4}{^{\circ }}$), which allows to maximize transmitted laser power. A thermal powermeter (Thorlabs, PM16-401) is used to measure the average laser power when no water vapor is present in the cell, i.e., during background measurements, when the cell is flushed with synthetic air. During measurements a fiber splitter with 99:1 split ratio (Thorlabs, TW1300R1A1) is used to monitor the laser power with an InAsSb photodetector (Thorlabs, PDA10PT-EC). Due to the stability of the laser diode in use over typical time periods between calibrations, no wavelength locking or power correction of the photoacoustic signal had to be applied.

The microphone in use is an electret condenser microphone (Knowles, EK-23028) with a specified humidity sensitivity of 0.02 dB/% RH. Signals are preamplified with a tenfold gain, before sampling at 51.2 kHz with a 24 bit ADC (National Instruments, NI 9234) and processing with a real-time embedded controller (National Instruments, NI cRIO-9031) is carried out. This controller features a function generator for generating the laser modulation signal and a digital lock-in amplifier for phase-sensitive detection, implemented on a reconfigurable field programmable gate array (FPGA). All signals are acquired with an integration time of 1 s. Background signal correction is carried out on the real-time processor of the controller.

The PA cell temperature and the gas temperature approximately 100 mm upstream of the cell are controlled to $35.0\pm 0.2\,^{\circ }\hbox {C}$ by two heating cartridges (125 W each) integrated into the stainless steel cell and heating tape around the upstream piping. The heating elements are controlled by a PID-controller implemented on the real-time embedded controller, which is supplied with the cell temperature and the gas temperature upstream of the cell measured with resistance temperature detectors (PT100, 1/3 DIN). A scroll pump in combination with a critical orifice with ${350}\,\upmu \hbox {m}$ nominal diameter is used to maintain a constant volumetric flow rate of ${0.75}\,\hbox {slpm}$ through the cell. The critical orifice has the additional benefit of inhibiting noise from the downstream pump reaching the cell. Directly upstream of the PA cell, a pressure controller maintains a constant pressure of 800(5) hPa inside the cell.

3.2 Humidity generation

Synthetic air or molecular nitrogen (Messer, for properties see Table 2) is either directly routed to the photoacoustic cell for the measurement of the background signal and noise, or humidified with a custom-made two-pressure humidity generator. The humidity generator consists of a pre-saturator, a heat exchanger and a saturator, where the latter two components are placed in a temperature-controlled water bath. Supplied zero gas is humidified in the presaturator to approximately 95% relative humidity at room temperature by passing the gas through a porous ceramics with honeycomb structure (IBIDEN Ceram) in a bath of distilled water. After pre-saturation, the gas is cooled and saturated to the desired saturation vapor pressure in a coiled tube heat exchanger combined with a saturator, which is formed by a milled channel in a stainless steel block, halfway filled with distilled water. The temperature of the water bath can be controlled to values between 1 and ${20}\,^{\circ }\hbox {C}$ with an uncertainty of ${0.16}\,^{\circ }\hbox {C}$. Setting the pressure in the saturator with a pressure controller in the range of 1–8 bar ($\pm 2\ {\mathrm{hPa}}$) allows to calculate the set saturation water vapor pressure or mole fraction [39, 40]. Uncertainties for the water vapor mole fractions in the two-pressure humidity generator have been calculated according to Meyer et al. [41]. The humidified air can then either be passed directly to the PA cell, or passed through the temperature controlled gas diluter [42], where the zero gas is mixed with the humidified gas based on binary weighted critical flows. This way, dilution ratios down to 1 : 31 have been used to further lower the water vapor mole fraction.

Table 2 Supplier specification for composition and relevant trace levels of synthetic air and nitrogen used in measurements

3.3 Correction of the photoacoustic phase

The speed of sound in the PA cell and hence the resonance frequency of the resonator is a function of the gas temperature and pressure, as well as the water vapor mole fraction [43]. To accurately determine the PA signal at varying water vapor mole fractions, a change in the resonance frequency either has to be actively tracked with the modulation frequency or corrected for. The measurement system in use is only capable of reliably tracking the resonance frequency at water vapor mole fractions above 1000 ppm and exhibits phase errors too large for the targeted accuracy. Therefore, the modulation frequency is held constant for all measurements with one carrier gas and the phase of the measured signal is then corrected according to the procedure described in the following. A correction of the PA amplitude was not carried out, because signal losses in the amplitude are low for the given Q-factor and the anticipated resonance frequency shifts (see Sects. 4.1 and 4.2).

In the proximity of the resonance peak, the phase of the photoacoustic signal can be approximated by a linear function of the frequency shift with slope $a_{\phi }$. Using this function, the phase measured at frequency $f_0$ and water vapor mole fraction $x_{{\rm H}_2{\rm O}}$ can then be corrected to give the phase at the actual resonance frequency, $f_{\mathrm{res}}$:

$$\begin{aligned} \phi (f_{\mathrm{res}},x_{{\rm H}_2{\rm O}})&=\phi (f_{0},x_{{\rm H}_2{\rm O}}) + a_{\phi }{\cdot } \left( f_{\mathrm{res}}-f_{0}\right) . \end{aligned}$$

(27)

The slope $a_{\phi }$ can be determined from a measurement of the PA response around the resonance and the unknown $f_{\mathrm{res}}$ is calculated by using the fact that for a longitudinal resonator the resonance frequency is given by

$$\begin{aligned} f = m_j\frac{c}{2\,L_{\mathrm{res}}}, \end{aligned}$$

(28)

where c is the speed of sound, $m_j$ is a non-negative integer, characteristic for the chosen resonance mode, and $L_{\mathrm{res}}$ is the effective length of the resonator. When the resonance frequency and speed of sound are known at a reference point (denoted by the subscript 0), the actual resonance frequency can be approximated by

$$\begin{aligned} f_{\mathrm{res}}(x_{{\rm H}_2{\rm O}})&= {f_{0}}\frac{c(f_{0},x_{{\rm H}_2{\rm O}})}{c_0}. \end{aligned}$$

(29)

The speed of sound in the gas mixtures was calculated according to Zuckerwar [43], as it can be described to great accuracy by theory at various temperatures and pressures. For the nitrogen mixture, however, no virial correction of the speed of sound was carried out.

3.4 Measurement

First, photoacoustically excited resonance curves were recorded at steady water vapor mole fractions of 4900 ppm in synthetic air and 11821 ppm in nitrogen, to determine the reference speed of sound and the reference resonance frequency for later correction of the phase according to Eq. (27). High water mole fractions were used to ensure a high signal to noise ratio (SNR). Resonance frequency and quality factor (Q-factor) were determined from a nonlinear curve fit of a Lorentzian function to the microphone signal power, which was measured at modulation frequencies in a $\pm 400\ \hbox {Hz}$ range of the resonance frequency with a resolution of 25 Hz. The resonance frequency is the frequency with maximum power and the Q-factor is the ratio of the resonance frequency to the full frequency width at half the maximum (FWHM) of the measured resonance curve. All following measurements were then conducted with the laser modulated at the determined resonance frequency.

Before each measurement series with synthetic air or nitrogen, the background signal, ${\mathbf {S}}_{BG}=(S_{BG,I},\,S_{BG,Q})^T$, was acquired for 60 s, after flushing the PA cell with the respective zero gas for approximately 20 minutes. Here, I and Q denote the in-phase and quadrature components of the lock-in amplifier signal, respectively. Subsequently, the photoacoustic signal in the humidified gas, ${\mathbf {S}}_{m}=(S_{m,I},\,S_{m,Q})^T$, was measured and the actual signal amplitude, S, and phase, $\phi$, were calculated after phase-correct background correction. This was achieved by subtracting the mean of the background signal of the corresponding buffer gas before calculating amplitude or phase:

$$\begin{aligned} S&= \Vert {{\mathbf {S}}_m - \overline{\mathbf {S}}_{BG}}\Vert \nonumber \\&= \sqrt{(S_{m,I} - \overline{S}_{BG,I})^2 + (S_{m,Q} - \overline{S}_{BG,Q})^2}, \end{aligned}$$

(30)

$$\begin{aligned} \phi&= \arctan \left( {\frac{S_{m,Q} - \overline{S}_{BG,Q}}{S_{m,I} - \overline{S}_{BG,I}}}\right) . \end{aligned}$$

(31)

An Allan deviation analysis of the PA background signal for pure synthetic air showed that deviations in the background signal due to drift over the time necessary for each measurement series are below the noise level at 1 s integration time. For this reason and the fact that the overall uncertainty is dominated by the uncertainty in the provided humidity, fluctuations of the background signal are not considered in the evaluation.

Starting from initial water vapor mole fractions (11435 ppm in synth. air and 11821 ppm in ${{\rm N}_2}$), the water concentration was incrementally decreased. After reaching the minimum concentration (124 ppm and 132 ppm, respectively) the water vapor concentration was increased again until reaching the maximum measured concentration (22154 ppm and 20278 ppm, respectively). This way, each measurement at a specific water vapor concentration is only taken once, but the interleaved measurements give a measure of repeatability. For each mole fraction set, the PA signal was recorded for 30 s after attaining a steady signal level. Mole fractions below 3900 ppm were generated in combination with the gas diluter.

3.5 Data analysis

The amplitude of the postulated nonlinear function for the PA response of water vapor in air, Eq. (26), was fit to the measured PA amplitude in a weighted least-squares sense, using a commercial curve fitting software [44]. Mole fraction weighted signal amplitudes were used to force minimization of the relative error, as otherwise large relative errors are tolerated for low signal levels in favor of small absolute errors at high amplitudes. The iterative trust region reflective solver was used to determine the best-fit values of the five parameters and coefficients $C_{\rm cell}$, $B_{\rm cell}$, $c_1$, $c_2$ and $c_3$. Starting values for the coefficients $c_1$ to $c_3$ were calculated using the rate coefficients given in Table 1 and setting $E_{{\rm H}_2{\rm O}^*}\,{=}\,1595\ \,{\rm cm}^{-1}$ (i.e., equal to the energy of the ${\rm H}_{2}{\rm O}$(0,1,0) level) and

$$\begin{aligned} E_{\mathrm{inst}}=h\,\nu -4\,E_{{\rm H}_2{\rm O}^*}. \end{aligned}$$

(32)

For measurements in humidified nitrogen, the oxygen mole fraction of the carrier gas, $x_{{{\rm O}_2},\mathrm {{dry}}}$, in $c_1$ and $c_2$ (Eqs. (19) and (20)) is set to zero. The conversion efficiency then is equal to unity (cf. Eq. (18)) and, as a result, the PA response of water vapor, Eq. (26), in nitrogen reduces to a simple second-degree polynomial with the fit parameters $C_{\rm cell}$ and $B_{\rm cell}$. Therefore, the coefficients $c_1$ to $c_3$ cannot be determined from measurements in humidified nitrogen.

In all of the presented figures, error bars for the PA amplitude mark the standard deviations calculated for the measured signal during the measurement time. Error bars for the phase indicate the uncertainty in the measured phase, calculated according to the GUM [45] using Eq. (27), while error bars for the mole fraction mark the uncertainty (95%) in the mole fraction (see Sect. 3.2).

4 Results and discussion

4.1 Nitrogen

In humidified nitrogen, a resonance frequency of 4658 Hz was determined at the reference water vapor mole fraction of 11821 ppm. As explained before, the modulation frequency was held constant at this value for all subsequent measurements in nitrogen and the phase was corrected using Eq. (27). However, additional resonance curves at higher and lower water mole fractions were acquired. The determined resonance frequencies showed good agreement with the theoretical values calculated from Eq. (29). For the maximum and minimum water vapor mole fractions measured, the resonance frequencies calculated are 4664 Hz and 4650 Hz, respectively. The largest resulting resonance shift, which occurs for the smallest ${\rm H}_2{\rm O}$ concentration, is estimated to cause amplitude errors less than 0.4% for the evaluated Q-factor of the PA cell of 17.

The measured and background-corrected PA amplitude and phase for nitrogen is shown in Fig. 7, together with the determined polynomial fit. Figure 8 is a plot of the amplitude with logarithmic scales, better displaying a linear response at low mole fractions.

A nonlinear PA response and phase shift with increasing ${\rm H}_{2}{\rm O}$ concentration as is shown below for air would be measurable, if ${\rm N}_{2}$ would be excited in similar quantities as ${\rm O}_{2}$, because of the similar rate coefficients of (R13) and (R14).

Fig. 7

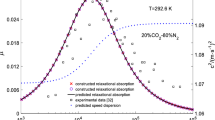
Measured and background-corrected amplitude and phase of the photoacoustic signal of water vapor in nitrogen at $35\,^{\circ }\hbox {C}$ and 800 hPa, together with the polynomial fit to the amplitude response. Dotted lines give the 95% (i.e., coverage factor ${k}=2$) functional bounds of the fit. Error bars are described in the text

Fig. 8

Logarithmic plot of the measured and background corrected amplitude of the photoacoustic signal of water vapor in nitrogen. For an explanation of the lines, see Fig. 7

For the evaluated range of water concentrations, it can be seen that the response is presumably linear for a large range of water fractions and a polynomial of second degree is sufficient to adequately capture and predict the PA amplitude response in nitrogen. In this range, the error in the humidity sensitivity of the electret microphone by a linear approximation is lower than 0.4% for the specified sensitivity of 0.02 dB/%RH. The best-fit values and 95% confidence intervals for $C_{\rm cell}$, and $B_{\rm cell}$ in Eq. (26) are given in Table 3 in terms of sensitivity and first-order sensitivity correction, respectively.

Table 3 Best-fit values and confidence interval (95%) of the parameters of the model, Eq. (26), determined from the curve fit to the measured and background-corrected PA amplitude of water vapor in nitrogen at $35\,^{\circ }\hbox {C}$ and 800 hPa

The initial offset of approximately ${22}{^{\circ }}$ of the corrected phase, shown in the lower part of Fig. 7, is arbitrary and is a result of the time delays in the electronics and signal processing for the given modulation frequency, affecting the measured phase. The phase, however, exhibits a small dip below 2000 ppm and a decreasing trend above. At low water fractions, the small measured decrease and recovery of less than ${1}{^{\circ }}$ may be the result of the competing V–T relaxation processes (R12) and (R14).

${\rm H}_{2}{\rm O}$ is much more efficient in the thermalization of vibrationally excited nitrogen than ${{\rm N}_2}$ itself or ${{\rm O}_2}$ and thus a phase shift and increase in sensitivity should be observable, if nitrogen is excited in substantial numbers. The small magnitude of the observed shift in phase, however, indicates the marginal contribution of the V–T relaxation of ${{\rm N}_2^*}$ to the PA source rate of heat production. Because the measured amplitude also remains practically linear over the full range of concentrations (to the extent measurable with the accuracy of the given setup), we conclude that the vibrational excitation of molecular nitrogen is of negligible importance in the PA signal generation process of water vapor in nitrogen, as well as in air. This justifies neglecting the V–V transfer process (R10) in the derivation of the three-state model. We would like to note at this point that it is still necessary to experimentally validate this assumption for higher modulation frequencies.

The values for the cell constant and the first-order correction differ from the values in air, mainly because of the modulation frequency and composition-dependent microphone sensitivity. As mentioned in Sect. 3.5, the coefficients $c_1$ to $c_3$ cannot be determined for the carrier gas nitrogen, the reason being the fast relaxation of ${{\rm H}_2{\rm O}^*}$ by ${{\rm N}_2}$, i.e., the rate ${\rm k}_{8}^{V{-}T}$ (or equivalently ${\rm k}_{{{\rm H}_2{\rm O}^*},{\rm M}}^{V{-}T}$) in reaction (R8). Without the possibility of vibrational coupling of ${{\rm H}_2{\rm O}^*}$ and ${{\rm O}_2^*}$, this reaction on its own induces full relaxation of ${\rm H}_2{\rm O}$(1,0,1) within typical PA modulation periods. For the ${{\rm N}_2}$ environment, this fast relaxation time results in a constant zero phase shift with respect to the excitation predicted by the model.

Due to the small magnitude of the observed phase shift, it cannot be fully ruled out that the measured variations are caused by minor temperature variations of the PA cell, inducing a shift of the resonance frequency. The reasons for the observable, superimposed trend with increasing water mole fractions are still unclear, but changing microphone sensitivity could be one possible source of origin. An error in the correction of the resonance frequency could be ruled out, as the calculated phase at resonance was verified at several water vapor mole fractions with additionally acquired resonance curves.

4.2 Synthetic air

The resonance frequency at the measurement temperature and pressure, determined for humidified synthetic air at the reference water vapor mole fraction of 4900 ppm, is 4586 Hz. Background measurement and measurements of the PA signal in humidified synthetic air were conducted at this modulation frequency. For the maximum and minimum water vapor mole fractions measured, the resonance frequencies calculated according to Eq. (29) are 4598 and 4584 Hz, respectively. Experimental determination of the resonance frequency at several water vapor mole fractions confirmed the theoretical calculation. The largest resulting resonance shift, which occurs for the largest ${\rm H}_2{\rm O}$ concentration, is estimated to cause amplitude errors less than 0.8% for the evaluated Q-factor.

Fig. 9

Measured and background-corrected amplitude and phase of the photoacoustic signal of water vapor in synthetic air at $35\,^{\circ }\hbox {C}$ and 800 hPa. Solid lines are evaluated from the fit of the three-level model to the measured and background-corrected PA amplitude. The phase evaluated from the model fit is offset by $-7.7{^{\circ }}$. Dotted lines give the 95% (i.e., coverage factor ${k}=2$) functional bounds of the fit. Error bars are described in the text

4.2.1 PA amplitude and phase

Fig. 10

Logarithmic plot of the measured and background-corrected amplitude of the photoacoustic signal of water vapor in synthetic air. For an explanation of the lines, see Fig. 9

Figure 9 shows the measured and background-corrected PA response for water vapor in synthetic air. The solid line in the upper panel is the fit of the PA amplitude response, calculated by fitting the amplitude of the model function (absolute value of Eq. (26)) to the measured PA amplitude data with the given starting values for the model parameters and coefficients. Dashed lines again show the 95% confidence bounds for the fit and a plot of the PA amplitude with logarithmic scales is shown in Fig. 10.

The lower panel of Fig. 9 shows the measured and corrected phase of the PA signal, together with the phase calculated from Eq. (22) with the coefficients estimated from the amplitude fit. Because of the different modulation frequency, the absolute value of the phase in synthetic air cannot be directly compared to the phase measured in nitrogen. The measured phase again includes a constant arbitrary phase shift from the specific time delays at the given modulation frequency. For the purpose of an easier comparison of measured and modeled phase, the model phase is offset by ${-7.7}{^{\circ }}$.

Estimated best-fit parameters and coefficients are given in Table 4, where $C_{\rm cell}$, and $B_{\rm cell}$ again have been given in terms of sensitivity and first-order sensitivity correction, respectively. The calculated sensitivity of $9.28\,{\upmu \hbox {V/ppm}}$ is approximately the maximum achievable sensitivity, which is reached when the conversion efficiency ${\varvec{\eta }}\rightarrow 1$ in the limit of large water vapor mole fractions. In this limit, ${{\rm H}_2{\rm O}^*}$ is thermalized by ${\rm H}_{2}{\rm O}$, before V–V transfer to ${\rm O}_{2}$ can occur. One may notice the high uncertainty in the value of the first-order sensitivity correction, which comes from the limited range of water vapor concentrations used for calibration. To decrease the uncertainty, a larger range would be necessary, but measuring at even higher concentrations may require higher-order terms, as the linear approximation of the Beer–Lambert law is invalidated.

Table 4 Best-fit values and uncertainties of the parameters and coefficients of the model, Eq. (26), determined from the nonlinear curve fit to the measured and background-corrected PA amplitude of water vapor in synthetic air at $35\,^{\circ }\hbox {C}$ and 800 hPa

Figure 11 shows the relative residual of the model response, which is, for a given microphone signal, the difference of the water vapor mole fraction predicted by the model and the mole fraction set by the humidity generator. With the estimated parameters and coefficients, residual mole fractions are below 4% above 500 ppm water vapor mole fraction. At lower fractions, the decreasing relative accuracy of the combination of humidity generation and PA measurement setup results in increasing deviations of the model from the measured response. Therefore, it is inconclusive whether the model is capable of returning satisfying predictions for the PA response for mole fractions down to the ppm level with the assumptions made in the derivation. Validation with a larger range of concentrations, especially below 1000 ppm, and a setup of combined higher accuracy would allow a much preciser determination of the model coefficients.

Fig. 11

Relative residual of water vapor mole fraction for the model fit. Both, vertical and horizontal error bars mark the uncertainty (95%) of the humidity generation

Overall, the derived model shows excellent capability of reproducing the functional relationship between the water vapor mole fraction in air and the measured PA amplitude response. The additional close agreement between measured and predicted phase response reassures that the model describes the main processes involved in release of kinetic energy by relaxation of ${\rm H}_{2}{\rm O}$ from low lying vibrational states. Also, considering the trend of decreasing phase observed in the nitrogen buffer gas, which presumably is independent of the relaxation process, further decreases the differences in the measured and predicted PA phase response for water vapor in air. Measured and trend-adjusted phase values in Fig. 9 below the reference point concentration of 4900 ppm should be decreased, whereas values above should be increased.

An idea briefly discussed in Sect. 2.2.2 is the use of the complex signal for finding the best-fit parameters. Fitting the complex PA signal gives parameter values in close agreement to the values determined by only fitting the amplitude response. However, the large uncertainty in the measured phase may introduce large systematic errors, deteriorating the estimated values. For devices with an accurate resonance frequency tracking functionality implemented, a precise relative measurement of the signal phase may be possible and allow enhancing the parameter estimation by the simultaneous use of the entire information available, i.e., measured amplitude and phase.

4.2.2 Sensitivity and PA conversion efficiency

Figure 12 shows the sensitivity of the measurement setup and the overall PA conversion efficiency calculated from Eq. (18) with the determined fit parameters. The sensitivity equals the derivative of the signal amplitude with respect to the water vapor mole fraction. It is calculated numerically from the determined best-fit model function.

The PA conversion efficiency asymptotically approaches approximately 19.2% in the limit of small mole fractions of water vapor. As a consequence, the sensitivity also reaches only about 19% of the maximum sensitivity (cf. Table 4) in this region, where the attenuation of irradiated power is negligible. In the process of heat production, this value corresponds to the energy released instantaneously after radiative excitation, i.e., $E_{\mathrm{inst}}$, plus the energy released by the V–T relaxation of ${{\rm H}_2{\rm O}^*}$ or ${{\rm O}_2^*}$ by collision with either ${\rm O}_{2}$ or ${\rm N}_{2}$. For an excitation energy equal to $7327\ \,{\rm cm}^{-1},$ the photoacoustically available energy is approximately equal to $1400\ \,{\rm cm}^{-1}$ per exited molecule at the conditions of measurement. The large residual energy, in the low concentration limit, is lost in vibrationally excited oxygen, due to its long relaxation time. Increasing the water vapor mole fraction up to 16,000 ppm increases the PA conversion efficiency and the heat production rate up to the point, where the full energy (99%) is released within the period of modulation. However, before this point is reached, decreased irradiance due to absorption deteriorates the sensitivity for the presented setup. The attenuation, calculated from $B_{\rm cell}$, rises above 1% at approximately 1400 ppm and initiates a transition to decreasing sensitivity. Maximum sensitivity for the given cell is reached at 4400 ppm. For PA spectroscopy setups where absorption path lengths are much shorter (e.g., in QEPAS), attenuation effects may be delayed to higher water vapor concentrations. Increasing modulation frequency, however, also delays reaching the full conversion efficiency to higher concentrations (cf. Fig. 12).

Fig. 12

Sensitivity of the PA measurement setup calculated numerically from the determined best-fit model function (800 hPa and $35\,^{\circ }\hbox {C}$), together with the determined overall PA conversion efficiency at various pressures and modulation frequencies (all at $35\,^{\circ }\hbox {C}$)

With the value of the sensitivity in the limit of low concentrations, $s_0$, the theoretical $3\sigma$ limit of detection can be estimated:

$${\rm LOD}_{{\rm H}_2{\rm O}}= \frac{3\,\sigma _{{\rm noise}}}{s_{0}}=38\ {\rm ppm},$$

(33)

where $\sigma _{\mathrm{noise}}$ is the standard deviation of the measured PA amplitude in the background measurement at an integration time of 1 s. Neglecting the nonlinear nature of the PA response and taking a value of the sensitivity close to the maximum observed would result in underestimating the LOD by approximately a factor of five.

The model may also be used to explain the sensitivity characteristics of the photoacoustic hygrometer of Tátrai et al. [11] (their Fig. 4). In their work, the measured sensitivity at a pressure of 800 hPa roughly remains constant below 250 ppmV, from where it steadily increases up to approximately 5000 ppmV. Above, the sensitivity starts to decrease again. This behavior closely matches the sensitivity demonstrated in this work.

The PA conversion efficiency given in Eq. (18) and shown in Fig. 12 is a function of the number density, which itself is a function of measurement pressure and temperature according to the ideal gas law. In a typical pressure and temperature-controlled photoacoustic setup, these two variables can be varied to some extent; therefore, it is beneficial to identify favorable magnitudes for the state variables, which maximize the conversion efficiency. In Eq. (18) the number density, $n_0$, only appears in combination with $c_3$, which is the rate coefficient for the V–T relaxation of ${{\rm O}_2^*}$ by collision with ${\rm H}_2{\rm O}$, i.e., ${\rm k}_{{\rm O}_2^*,{\rm H}_2{\rm O}}^{V{-}T}$ (cf. Eq. (21)). Increasing pressure can thus be viewed as proportionally increasing the V–T relaxation rate ${\rm k}_{{\rm O}_2^*,{\rm H}_2{\rm O}}^{V{-}T}$, which results in accelerated deexcitation of ${{\rm O}_2^*}$ and consequently in an increased PA conversion efficiency when relevant amounts of water vapor are present. It follows that the conversion efficiency can be maximized by maximizing the measurement pressure. This behavior is shown in Fig. 12 for the measurement pressure of 800 hPa, as well as higher and lower pressures. Contrary to the pressure dependence, the conversion efficiency is maximized by minimizing temperature. When the modulation frequency is increased, less heat is released in phase with the modulation and therefore the conversion efficiency is decreased (cf. Fig. 12). In general the PA signal, given by Eq. (26), will also depend on pressure and temperature through the characteristics of the microphone, hence the overall dependence of the PA signal on pressure and temperature can only be calculated for a specific setup.

The best-fit values for the coefficients $c_1$ and $c_2$ are slightly lower than the starting values calculated from literature values. Due to the convoluted dependencies of these coefficients on the rate coefficient and energies, it is difficult to draw direct conclusions about the involved processes. To assess relevant physical constants in these model coefficients, Figs. 13 and  14 show the local relative sensitivity of the PA conversion efficiency and the phase shift on the four remaining rate coefficients of the model and on the energy of the ${{\rm H}_2{\rm O}^*}$ reservoir, $E_{{\rm H}_2{\rm O}^*}$, at the conditions of measurement. The shown sensitivity gives the local relative change in $\eta$ or $\phi$ per relative change in the rate coefficient or energy at the given water concentration. The relative sensitivity of $\eta$ is equal to the relative sensitivity of the signal amplitude. It can be seen that the magnitude of the conversion efficiency as well as the phase shift is most sensitive to $E_{{\rm H}_2{\rm O}^*}$. The value for the energy of the reservoir determines the energy released instantaneously after radiative excitation (cf. Eq. (32)), which at low water vapor concentrations is the main contribution to the PA heat source rate and therefore also to $\eta$ and the signal amplitude. This explains the large sensitivity of $\eta$ to $E_{{\rm H}_2{\rm O}^*}$ at low concentrations. Figures 13 and  14 also show that directly applying literature values for rate constants and the energy of the reservoir in the model, instead of the fit parameters $c_1$ and $c_2$, requires the accurate determination of all of the rate constants of the involved reactions to accurately predict the amplitude and phase response of a PA hygrometer over the range of mole fractions studied in this work. As uncertainties and therefore probably also errors in the literature rate coefficients are generally large (e.g., Huestis [25]), this inevitably will lead to large deviations between model prediction and experimental measurements. However, this underlines the benefit of the proposed model function of summarizing four coefficients: (${{\rm k}_{{\rm H}_2{\rm O}^*,\mathrm{M}}^{V{-}T}}$, ${{\rm k}_{{\rm H}_2{\rm O}^*,{\rm O}_2}^{V{-}V}}$, ${{\rm k}_{{\rm H}_2{\rm O}^*,{\rm H}_2{\rm O}}^{V{-}T}}$ and $E_{{\rm H}_2{\rm O}^*}$) in the two coefficients $c_1$ and $c_2$, which can be determined from calibration.

Only at large concentrations, where $\eta$ approaches unity, the conversion efficiency and therefore also the PA signal amplitude become insensitive to the constants and a simple second-order polynomial suffices to describe the signal amplitude. At low water concentrations, the signal amplitude only depends on ${{\rm k}_{{\rm H}_2{\rm O}^*,\mathrm{M}}^{V{-}T}}$, ${{\rm k}_{{\rm H}_2{\rm O}^*,{\rm O}_2}^{V{-}V}}$, and $E_{{\rm H}_2{\rm O}^*}$. Therefore, the PA response for low water concentrations can be fully described by the coefficients $c_1$ and $c_2$ in addition to the cell parameters. This also opens up the possibility of determining the ratio of ${{\rm k}_{{\rm H}_2{\rm O}^*,\mathrm{M}}^{V{-}T}}$ and ${{\rm k}_{{\rm H}_2{\rm O}^*,{\rm O}_2}^{V{-}V}}$ by measuring the PA response at low concentrations for excitation into the ${\rm H}_2{\rm O}$(0,1,0) state, where $E_{{\rm H}_2{\rm O}^*}$ is accurately known. Additionally, in such an experiment the model describes the full relaxation path, and uncertainties introduced by model assumptions are negligible.

Fig. 13

Relative local sensitivity of the PA conversion efficiency on rate coefficients, ${\rm k}_{{i}}$, and on the energy of the $\mathrm {H}_2{\rm O}^*$ reservoir, $E_{\mathrm {H}_2{\rm O}^*}$. The sensitivity is calculated with literature rate coefficients and for the conditions of measurement (800 hPa, $35\,^{\circ }\hbox {C}$, 4586 Hz and 20.5% $\mathrm {O}_2$ fraction)

Fig. 14

Relative local sensitivity of the PA phase shift on rate coefficients, ${\rm k}_{\mathrm{i}}$, and on the energy of the $\mathrm {H}_2{\rm O}^*$ reservoir, $E_{{\rm H}_2{\rm O}^*}$. The sensitivity is calculated with literature rate coefficients and for the conditions of measurement (800 hPa, $35\,^{\circ }\hbox {C}$, 4586 Hz and 20.5% $\mathrm {O}_2$ fraction)

The third coefficient, $c_3$, is equivalent to the rate coefficient of the V–T relaxation of ${{\rm O}_2^*}$ by collision with ${\rm H}_{2}{\rm O}$, i.e., ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\rm{H}}_2{\rm{O}}}$ in reaction (R13). The determined value is about an order of magnitude higher than the rate measured by Bass et al. [26, 27, 30]. Unfortunately, the latter, much-cited rate coefficient is, to our knowledge, the only literature value available for this process. When constraining the value of $c_3$ (and thus ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\rm{H}}_2{\rm{O}}}$) to the reaction rate coefficient stated by Bass et al., it is not possible to reproduce the measured PA response with the derived model function, Eq. (26). This is the result of an underestimation of the phase-delayed PA heat source rate component due to reaction (R13) (cf. last term in brackets in Eq. (S2)). For this reason we suspect that the value stated for ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\rm{H}}_2{\rm{O}}}$ by Bass et al. may be underestimated. Figure 14 shows the high sensitivity of the phase shift to the rate coefficient in question. This implies that ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\rm{H}}_2{\rm{O}}}$ may be directly and accurately determined from a fit of the model to PA measurements of excitation into the ${\rm H}_2{\rm O}$(0,1,0) state considering the measured phase. The sensitivity of $\eta$ and the signal amplitude to the rate coefficient are shown to be negligible (cf. Fig. 13). However, this changes when ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\rm{H}}_2{\rm{O}}}$ is set to the value determined by the fit parameter $c_3$. In this case, the reaction coefficient strongly contributes to $\eta$ in the range of 1000–10,000 ppm. This also explains the inability of the model to reproduce the measured amplitude when ${\rm k}^{V{-}T}_{{\mathrm{O}}_2^*,{\mathrm{H}}_2{\mathrm{O}}}$ is constrained to the literature value.

5 Conclusions

In the present work, we demonstrated the significant and unfavorable effects of relaxation processes involving molecular oxygen, on the vibrational photoacoustic measurement of water vapor in air. The strong resonant coupling of the first vibrationally excited state of water vapor, ${\rm H}_{2}{\rm O}$(0,1,0), with the long-living, first vibrationally excited state of molecular oxygen, ${\rm O}_{2}$(1), leads to a relaxation time that is large in comparison to typical modulation periods in photoacoustic spectroscopy. This results in a nonlinear photoacoustic signal response which has to be taken into account in measurements of water vapor in atmospheric environments. Neglecting relaxation losses and assuming a linear functional relationship between the number of absorbing molecules and the measured PA signal as it is commonly done may lead to indeterminate errors when extrapolating the signal outside the measurement range.

We propose a simplified model in the form of Eq. (26), physically approximating the main relaxation processes involved. The derived model describes the microphone signal measured in a resonant photoacoustic cell and a mixture of air and water vapor, after radiative excitation from the ground state into vibrational ${\rm H}_{2}{\rm O}$(1,0,1) state. Furthermore, the suggested model may easily be adapted to lower and possibly also higher excitation energies. Additionally, adaption of the model to predict the PA response for other systems of measured species and carrier gas, where the vibrational coupling to oxygen is of importance, seems feasible (e.g., ${\rm {CH}}_4$ in air [17]). Validation of the model was performed for the range of approximately 100–22,000 ppm water vapor mole fraction in synthetic air.

The presented PA measurement results of water vapor in nitrogen show that the process of excitation of nitrogen by V–V energy transfer does not contribute significantly to the decrease of the signal for water vapor mole fractions greater than 100 ppm and at typical modulation frequencies. Hence, sensitivity losses in air are fully attributable to oxygen, and no losses are to be expected in nitrogen environments. Thus, applying corrections based on photoacoustic water vapor measurements in nitrogen to measurements made in air (e.g., [5]) can lead to significant errors. Contributions arising from minor air constituents (e.g., $\mathrm {Ar}$, ${{\rm CO}_2}$) have been neglected in the current analysis. Consideration of relevant relaxation processes of these constituents may lead to a more accurate, but possibly more complicated model.

The derived model contains three coefficients, $c_1$ to $c_3$, which summarize kinetic coefficients and are universal for a given excitation energy and carrier gas composition. The three coefficients should be practically independent of the measurement setup. Only minor temperature dependence should be observable, caused by the temperature dependence of the rate coefficients. Thus, determining $c_1$ to $c_3$ once allows to predict the response of a PA hygrometer outside the calibration range. Best-fit results for the two device parameters, $C_{\rm cell}$ and $B_{\rm cell}$, and the three coefficients, determined from measurement data are given in Table 4.

The two device parameters, $C_{\rm cell}$ and $B_{\rm cell}$, correlate to measurement sensitivity and first-order correction of the cell constant $C_{\rm cell}$. In environments of sufficiently low water vapor concentrations, where a decrease of irradiance due to absorption and other second-order effects in the microphone signal may be neglected, the sensitivity is the only setup specific parameter. When the coefficients of the kinetic model, $c_1$ to $c_3$, are accurately determined, the calibration of a photoacoustic hygrometer (i.e., the determination of $C_{\rm cell}$) in this region may be accomplished by a background measurement combined with a single, accurate reference concentration measurement. The presented findings suggest that the derived model should then allow extrapolation within the region of low water vapor concentrations. When measurements have to be accomplished at high water vapor concentrations, where second-order effects cannot be neglected, the two device parameters, $C_{\rm cell}$ and $B_{\rm cell}$, can be determined solely from calibration at high water vapor concentrations. Accurately determined coefficients of the PA conversion efficiency may allow accurate extrapolation to lower water vapor fractions.

Evaluation of the model coefficient $c_3$ opens up the possibility of estimating the V–T relaxation rate coefficient of ${\rm O}_{2}$(1) by ${\rm H}_{2}{\rm O}$, i.e., of reaction (R13). The estimated value determined in this work is an order of magnitude larger than the value measured by Bass et al. [26, 27, 30], which apparently is the only literature source available for this rate. As this value is also of relevance to the atmospheric radiative transfer community, the discrepancy will be further investigated.