Further insight into the oscillating photocarrier grating technique: influence of the oscillation amplitude

Abstract

Allowing for the simultaneous determination of the photocarriers drift mobilities and their small-signal recombination lifetime, the Moving photocarrier Grating Technique (MGT) is a useful characterization tool for photoconductive semiconductors. This technique is based on measuring the steady-state direct current induced by an interference pattern (IP) moving at a constant velocity between two coplanar ohmic contacts deposited on the semiconductor. The main drawback of the technique is the low level of the signal to be measured, which can be masked by noise. The Oscillating Photocarrier Grating technique (OPG), where the IP oscillates at a constant speed, has been proposed as an alternating current version of MGT, providing a higher signal-to-noise ratio. The IP oscillation is produced by the phase modulation of one of the interfering beams. Using the multiple trapping model we deduce the expression of the current density generated by OPG in a photoconductor. We observed theoretically and experimentally that OPG is not equivalent to MGT for the previously used amplitude of oscillation, especially when the IP moves at high speeds. However, we show that the desired equivalence between both techniques could be recovered by increasing the amplitude of oscillation. A phase modulator capable of achieving such amplitudes is required for the correct implementation of OPG.

1 Introduction

The Oscillating Photocarrier Grating technique (OPG) was initially proposed by Ventosinos et al. [1] as an Alternating Current (AC) version of the Moving photocarrier Grating Technique (MGT). The latter technique is based on measuring the Direct Current (DC) induced in a photoconductor by a monochromatic illumination, that consist of an Interference Pattern (IP) moving at constant speed from one electrical contact to the other on a uniform background of higher intensity. This illumination is achieved by introducing a small frequency difference (∆ω) between two interfering monochromatic beams of much different intensities, being the IP speed proportional to ∆ω. The current induced between the coplanar ohmic contacts is entirely caused by the illumination and does not require the presence of an external electric field; for this reason, the effect is also known as the photo-electromotive force [2]. The current direction is determined by the charge of the majority carrier, which makes the technique useful for the immediate determination of the sample doping type. Haken et al. [3] proposed determining the drift mobilities and the small-signal recombination lifetime (τʹ), by fitting with a theoretical equation the steady-state current induced by different IP speeds. Later, Witt et al. [4] observed that, when the IP spatial period ($\Lambda$) is considerably larger than the ambipolar diffusion length of the photocarriers and their small-signal recombination lifetime (τʹ) is much longer than the dielectric relaxation time¹ in the material, τʹ is related to the angular frequency difference that maximizes the current, ∆ω_m, by the simple equation, $\tau^{\prime} = \Delta \omega_{m}^{ - 1}$.

Despite its simplicity and potential, MGT never achieved the popularity of other techniques used for the estimation of the mobilities, such as the Hall Effect measurements. The main drawback of MGT is the low level of the signal to be measured, which can be easily masked by noise at low temperatures or low light intensities, especially in poor photoconductors. To produce a greater signal-to-noise ratio, Ventosinos et al. [1] proposed OPG, which generates an AC signal in the material instead of a DC one. The advantage of measuring an AC signal is related to the possibility of using a lock-in amplifier to remove the electrical noise from the current. Hence, OPG has been used as a complement to MGT for low temperatures and low generation rates, when the signal induced by MGT is too low to be directly measured [5, 6].

In OPG the material is also illuminated with a monochromatic light that consists of a moving interference pattern on a uniform background of higher intensity, although its movement is periodic: it moves at a constant velocity from one contact to the other for half a period, while during the next half period it moves at the same speed but in the opposite direction. The AC signal is produced between the coplanar contacts as a result of the IP oscillation and it does not require the presence of an external electric field. Note that during each half period the OPG illumination corresponds exactly to that of MGT. As a consequence of the sample’s symmetry, the steady-state current induced by the movement of the interference pattern at a given constant velocity must be exactly the opposite of that produced with the opposite velocity. Previous works [1, 5, 6] assumed that the AC steady-state signal induced in the material by OPG consists of a square wave whose extreme values correspond to the steady-state current induced by MGT over each half period (which should be equal to each other in modulus). Therefore, the peak-to-peak amplitude of the alternating steady-state signal induced by OPG is two times the absolute value of the steady-state signal induced by MGT under the same experimental conditions. This assumption allows using OPG for the estimation of the MGT signal.

Recently, another technique have been proposed to produce an AC signal proportional to the DC signal induced by MGT: the Chopped Moving photocarrier Grating (CMG), which consist of chopping at a low frequency the weak beam in the standard MGT configuration [7]. Although it is simpler than OPG, the AC signal induced in the material by CMG is half the AC signal induced by OPG, and consequently it does not allow obtaining such a higher signal-to-noise ratio.

In this work, we develop a more fundamental analysis of OPG than those previously presented [1, 5, 6], since the current density expression is obtained using the multiple trapping model without making further assumptions. This model is well established for photoconductive materials such as hydrogenated amorphous silicon (a-Si:H), especially for the high temperatures and light intensities used here, where hopping conduction and hopping recombination are negligible [8,9,10]. By means of a numerical simulation with parameters typical for a-Si:H we test the above-mentioned assumption [1, 5, 6], which implies the proportionality between the AC current induced by OPG and the DC current induced by MGT. We observe that, with the IP amplitude of oscillation used previously [1, 5, 6], the currents cease to be proportional for high IP speeds (large values of ∆ω). However, we note that increasing the oscillation amplitude allows regaining the proportionality for the entire range of measurable ∆ω values. We perform measurements on a sample of undoped a-Si:H, presenting a complete description of the experimental procedure followed. Among other important things, we detail how to attain a precise calibration of the IP oscillation amplitude. Unfortunately, with the phase modulator that we have we could not achieve the amplitudes of oscillation that guarantee the proportionality between OPG and MGT currents in the entire range of ∆ω values. However, the new experimental results show the expected differences and similarities between both currents and the same tendencies observed in the numerical simulation, validating the new theoretical results presented. According to the new theoretical results, OPG would produce a current proportional to MGT if the previously used [1, 5, 6] IP amplitude of oscillation is at least multiplied by six.

The paper is organized as follows. A theoretical introduction to OPG is presented in Sect. 2, where an ideal relationship, similar to the previous one [1, 5, 6], is found between the steady-state DC signal induced by MGT and the steady-state AC signal induced by OPG. Details about MGT will be mostly omitted in this paper because they have been exhaustively given in Ref. [7]. Section 3 details the procedure followed for obtaining the expression of the current density induced by OPG in a photoconductor. Section 4 presents a theoretical comparison between the current induced by MGT and OPG in undoped a-Si:H. Section 5 describes the experimental methods, while the experimental results are presented and discussed in Sect. 6. The main conclusions of this work are summarized in Sect. 7.

2 Theoretical background

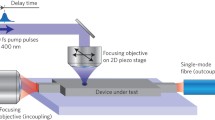
Figure 1 presents a schematic diagram of the OPG experimental configuration. A beam of (vertically) polarized laser light is divided in two by a Beam Splitter (BS). One of the beams is attenuated with a Neutral Density Filter (NDF), to obtain a large difference between both intensities. One of the beams passes through a Phase Modulator (PM), which introduces a triangular variation of its phase over time φ (t), with a period Γ and a peak-to-peak amplitude A_pp:

$$\varphi \left( t \right) = \left\{ {\begin{array}{*{20}l} {2A_{pp} t/\varGamma ,} & {t \in \left[ {0 ; \frac{\varGamma }{2} } \right]} \\ {2A_{pp}\left( {1 - t/\varGamma } \right), } & {t \in \left[ {\frac{\varGamma }{2} ; \varGamma } \right]} \\ \end{array} } \right. .$$

(1)

Fig. 1

Experimental setup of the Oscillating Photocarrier Grating technique (OPG). A laser beam is divided with a Beam Splitter (BS) and one of the two beams is dimmed with a Neutral Density Filter (NDF), thus its intensity gets much lower than that of the other beam. One beam passes through a Phase Modulator (PM) which generates a triangular variation of its phase over time. The beams are focused with Mirrors (M) to interfere between the contacts of the sample. The AC signal induced in the sample by the light is preamplified and its fundamental frequency component is measured with a lock-in amplifier

The beams are made to interfere at the region between the contacts of the sample using Mirrors (M). When one of the beams arrives perpendicularly to the sample as in Fig. 1, the spatial period of the interference pattern (Λ) is related to the angle between the incident beams (δ) by $\Lambda = \lambda /\sin \left( \delta \right)$, where λ is the wavelength of the laser light in air. Assuming spatially uniform intensity for each laser beam, it is obtained the following light intensity distribution as a function of time and position between the contacts (x) [1]:

$$I\left( {x,t} \right) = I_{1} + I_{2} + 2\gamma_{0} \sqrt {I_{1} I_{2} } \cos \left( {2\pi \frac{x}{ \Lambda } + \varphi \left( t \right)} \right),$$

(2)

where I₁ and I₂ are the intensities of the strong and the weak beams, respectively, and γ₀ is the interference quality factor, whose value is positive and less than 1 as a consequence of light scattering, mechanical vibrations and partial coherence of the beams. For a given value of $\Lambda$, the maximum distance that the IP travels along the x coordinate D_pp, is proportional to the oscillation amplitude of the beam phase A_pp, more precisely, $D_{pp} = A_{pp} {\Lambda} /\left( {2\pi } \right)$. The IP oscillation induces an AC signal in the sample and, after the electrical signal is preamplified, its fundamental frequency component is measured with a lock-in amplifier.

The assumption of spatially uniform illumination in the direction of the current (x direction) is justified if the beams’ diameters on the sample are much larger than the separation between the coplanar electrical contacts. Figure 1 resembles the experimental configuration of the Modulated Photocarrier Grating technique (MPG) [11], where the weak beam goes through a polarization modulator instead of a phase modulator. Unlike MPG, the modulator in OPG setup can be placed in the path of any of the two beams.

When the energy of the light beam is greater than the material gap, the average generation rate of free carriers in the material (G) is proportional to the flux of incident photons (F), and the proportionality constant (K) can be estimated from the following equation:

$$K\sim \frac{{\left( {1 - r} \right)}}{d}\left( {1 - e^{ - \alpha d} } \right),$$

(3)

where $r$ is the reflection coefficient of the frontal surface, d is the thickness of the film and $\alpha$ is the absorption coefficient of the material for the incident light energy [2]. It is not recommended to use light with energy much higher than the material’s gap, because in this situation, the light is totally absorbed near the surface of the material, and Eq. 3 is not valid anymore. In this case, the surface recombination cannot be neglected and the equations deduced in Sect. 3 may need modifications [12, 13].

From Eq. 2 we obtain the average generation rate induced in the material by OPG:

$$ \begin{aligned}G &= G_{0} + \Delta G_{0} \cos \left( {k x + \varphi \left( t \right)} \right) \\ &= G_{0} + \Delta G_{0} \left[ {\cos \left( {k x} \right)\cos \left( {\varphi \left( t \right)} \right) - \sin \left( {k x} \right)\sin \left( {\varphi \left( t \right)} \right)} \right],\end{aligned} $$

(4)

where $k=2\pi /\Lambda$. The uniform generation rate is given by G₀ = G₁ + G₂, where G₁ and G₂ come from I₁ and I₂, respectively. The amplitude of the harmonic generation rate is given by $\Delta G_{0} = 2\gamma_{0} \sqrt {G_{1} G_{2} }$. As a consequence of the large difference between the interfering beams intensities, the relation $\Delta G_{0} \ll G_{0}$ is verified.

During each half period, the OPG illumination corresponds to that of MGT with a frequency difference between the beams given by:

$$\Delta \omega = \pm \frac{{A_{pp} \omega_{o} }}{\pi },$$

(5)

where the positive sign corresponds to the movement of the interference pattern in one direction, while the negative sign corresponds to the movement in the opposite direction, and ω_o is the fundamental angular frequency of the OPG signal, which is related with its period by ω_o = 2π/Γ. Equation (5) is obtained equating the expressions of the IP velocities in OPG technique (± 2D_pp/Γ) with the expression of the IP velocity in MGT (∆ω/k) [7]. If $\Delta J_{MGT}$ corresponds to the steady-state current density induced by MGT in material while the IP is moving at a given constant speed in one direction, the steady-state current density induced by MGT for the opposite IP velocity is equal to $- \Delta J_{MGT}$. Figure 2 shows the signal induced by OPG in the material assumed in previous works [1, 5, 6], where the current induced during each half period corresponds exactly to the steady-state current induced by MGT. In this case, the amplitude of the first harmonic component of the signal, $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$, is proportional to the steady-state current induced by MGT with $\left| {\Delta \omega } \right| = A_{pp} \omega_{o} /\pi$ under exactly the same experimental conditions. More precisely:

$$\left| {\Delta J_{MGT} } \right|\left( {\left| {\Delta \omega } \right| = A_{pp} \omega_{o} /\pi } \right) = \frac{\pi }{4}\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right| = \sqrt 2 \frac{\pi }{4}\left( {\frac{{\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|}}{\sqrt 2 }} \right),$$

(6)

Fig. 2

Idealized relation between the steady-state current densities induced by the Oscillating Photocarrier Grating technique (OPG) and Moving photocarrier Grating Technique (MGT) for the same experimental conditions and when the interference pattern (IP) speed is the same in both techniques. This signal is a good approximation to the current induced by OPG, only when the time during which the interference pattern moves in one direction (Γ/2) is much longer than the time it takes the current to reach its new steady-state value after the sudden change of the IP direction of movement

where ($\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|/\sqrt 2$) corresponds to the module of the RMS current density measured by the lock-in amplifier. Equation (6) is obtained by calculating the first harmonic amplitude of the signal plotted in Fig. 2. In the previous papers [1, 5, 6], a fixed value is used for the oscillation amplitude of the phase, $A_{pp} = \pi /2$.

Note that the signal conjectured in Fig. 2 for the steady-state current density induced by OPG corresponds to an ideal case since a macroscopic current cannot change its value instantaneously, due to the inertia and the finite recombination lifetime of the photocarriers. A more realistic signal should include some type of continuous transient from $\left| {\Delta J_{MGT} } \right|{\text{ to }} - \left| {\Delta J_{MGT} } \right|$ and vice versa, with a certain finite duration $\tau_{t}$. The induced signal would tend to the ideal one when the time during the IP is moving in one direction (Γ/2) is much longer than the duration of the transient $\tau_{t}$. Therefore Eq. 6, which allows obtaining $\left| {\Delta J_{MGT} } \right|$ from the measurement of the current induced by OPG, should only be valid for sufficiently large periods of oscillation (Γ), or equivalently, for low enough frequencies of oscillation ($\omega_{o} = 2\pi /\varGamma$).

3 Deduction of the current density expression

To obtain the expression of the current density induced by OPG, without making assumptions about its shape, it is necessary to make a Fourier series expansion of the sine and cosine of the phase φ (t) (given by Eq. 1), and replace them into Eq. 4, corresponding to the mean generation rate induced in the material by OPG. Using elementary trigonometric properties, it is possible to express the non-uniform component of the generation rate as the sum of traveling harmonic waves of different frequencies (Ω) multiples of ${\omega }_{o}$ ($\Omega = i\omega_{o}$). Thus, Eq. 4 can be rewritten as:

$$\begin{gathered} G = G_{0} + Re\left\{ {\mathop \sum \limits_{{\Omega }} {} g_{\Omega } e^{{j\left( {kx + \Omega t} \right)}} } \right\}. \hfill \\ \hfill \\ \end{gathered}$$

(7)

Since $\Delta G_{0} \ll G_{0}$, it can be shown that $g_{\Omega } \ll G_{0}$ (see appendix A), which allows discarding the nonlinear terms in the fundamental equations. Therefore, the free carrier densities and the induced electric field can be found by adding the solutions obtained separately for each term within the braces of Eq. 7. The densities of free electrons (n) and holes (p), and the electric field (ξ), then become:

$$n = n_{0} + \mathop \sum \limits_{{\Omega }} {}Re\left\{ {\Delta n_{\Omega }\, e^{{j\left( {kx + \Omega t} \right)}} } \right\},$$

(8)

$$p = p_{0} + \mathop \sum \limits_{{\Omega }} {}Re\left\{ {\Delta p_{\Omega }\, e^{{j\left( {kx + \Omega t} \right)}} } \right\},$$

(9)

$$\xi = \xi_{ext} + \mathop \sum \limits_{{\Omega }} {}Re\left\{ {\Delta \xi_{\Omega }\, e^{{j\left( {kx + \Omega t} \right)}} } \right\},$$

(10)

where n₀ and p₀ are the concentrations of carriers generated by G₀, and ξ_ext is the externally applied electric field. Note that when taking a single term from the summation in Eq. 7, the generation rate corresponds mathematically to that of MGT, whose steady-state solution can be found in the literature [1, 7]. Each harmonic amplitude of Eqs. 8, 9 or 10 (∆n_Ω, ∆p_Ω or ∆ξ_Ω, respectively) depends only on the generation rate’s uniform component, G₀, and the same-frequency’s harmonic amplitude, g_Ω, but not on the rest (i.e. on g_Ω′ with Ω′≠ Ω). The precise expressions obtained with the multiple trapping model for a material with an arbitrary monovalent density of states can be found in appendix A of Ref. [7].

If we assume spatially periodic boundary conditions, the spatial average of the current density, J, coincides with the spatial average of the current density in a period $\Lambda$,

$$J = \frac{1}{\Lambda }\int_{0}^{\Lambda } {\left[ {\sigma \xi + k_{b} T\left( {\mu_{n} \frac{\partial n}{{\partial x}} - \mu_{p} \frac{\partial p}{{\partial x}}} \right)} \right]} dx = J_{0} + \Delta J_{OPG} .$$

(11)

k_b is the Boltzmann constant, T is the absolute temperature, μ_n and μ_p are the mobilities of free electrons and free holes, respectively, and $\sigma$ is the electrical conductivity,

$$\sigma = q\left( {\mu_{n} n + \mu_{p} p} \right) = \sigma_{0} + \mathop \sum \limits_{{\Omega }} {}Re\left\{ {\Delta \sigma_{\Omega }\, e^{{j\left( {kx + \Omega t} \right)}} } \right\},$$

(12)

where σ₀ and ∆σ_Ω are given by:

$$\sigma_{0} = q\left( {\mu_{n} n_{0} + \mu_{p} p_{0} } \right), \Delta \sigma_{\Omega } = q\left( {\mu_{n} \Delta n_{\Omega } + \mu_{p} \Delta p_{\Omega } } \right),$$

(13)

The diffusion currents, given by the second term within the square brackets in Eq. 11, are cancelled after integration. J₀ is the current density caused by the uniform generation rate, and it cancels when the external electric field is zero,

$$J_{0} = \frac{1}{\Lambda }\int_{0}^{\Lambda } {\sigma_{0} \xi_{ext} dx = \sigma_{0} \xi _{ext} } .$$

(14)

∆J_OPG corresponds to the current density induced by the periodic generation rate,

$$\Delta J_{OPG} = \frac{1}{\Lambda }\int_{0}^{\Lambda } {\sum\limits_{{\Omega }} {Re\left\{ {\Delta \sigma_{\Omega } e^{{j\left( {kx + \Omega t} \right)}} } \right\}} \sum\limits_{{\Omega^{\prime} }} {} {{}Re\left\{ {\Delta \xi_{{\Omega^{\prime}}} e^{{j\left( {kx + \Omega^{\prime}t} \right)}} } \right\}dx} } .$$

(15)

After distributing the product and integrating, it can be expressed as

$$\Delta J_{OPG} = \Delta J_{OPG}^{0} + Re\left\{ {\Delta J_{OPG}^{{\omega_{o} }} e^{{j\omega_{o} t}} } \right\} + Re\left\{ {\Delta J_{OPG}^{{2\omega_{o} }} e^{{j2\omega_{o} t}} } \right\} + \cdots .$$

(16)

In this work, we are only interested in the amplitude of the current induced at the fundamental frequency, $\Delta J_{OPG}^{{\omega_{o} }}$, whose expression depends on whether the oscillation amplitude of the phase, A_pp, is a multiple of π or not. The expressions obtained for each case are deduced in appendix A.

4 Numerical simulations

To numerically simulate the photoconductive behaviour of undoped a-Si:H, we use exactly the same density of states and material parameters of Ref. [7]. For given T and G₀ values, we initially obtain the uniform concentrations of free carriers, n₀ and p₀, by solving the continuity and the charge neutrality equations simultaneously [7]. We obtain then the harmonic terms’ amplitudes of the electron concentration (∆n_Ω), hole concentration (∆p_Ω) and the electric field (∆ξ_Ω). Replacing the values of ∆ξ_Ω and ∆σ_Ω (obtained from Eq. 13) into Eqs. 24 or 29, we obtain the modulus of the current density induced at the fundamental frequency. When A_pp is not a multiple of π, the expression of the current density results in an infinite summation (Eq. 29). To estimate $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$ we cut the sum at i = 8, since we observe that with this approximation at least three significant digits of precision can be assured. The procedure for calculating the steady-state current density induced by MGT (∆J_MGT) can be found in Ref. [7].

Figures 3 and 4 present the results obtained when the oscillation amplitudes of the phase are less than π and multiples of π, respectively. These were obtained with average experimental values of temperature, generation rate and spatial period of the IP (T = 200 K, G₀ = 5 × 10²⁰ cm⁻³ s⁻¹ y $\Lambda$= 6 × 10^–4 cm), although we observed that the qualitative relationships between the different curves are independent of the particular values of these parameters. The solid line corresponds to the exact value of $\left| {\Delta J_{MGT} } \right|$, while the dashed lines were obtained with Eq. 6 when $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$ is calculated from Eqs. 24 or 29.

Fig. 3

Steady-state current densities corresponding to the Moving photocarrier Grating Technique (MGT) as a function of the frequency difference between the interfering beams, obtained with a numerical simulation of undoped a-Si:H. The solid line corresponds to the exact values obtained with MGT, while the dashed lines were obtained using Eq. 6 with $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$ calculated for A_pp = 3π/4, π/2 and π/4, as indicated in the caption. The arrow shows the displacement of the maximum as the oscillation amplitude in OPG decreases

Fig. 4

Steady-state current densities corresponding to the Moving photocarrier Grating Technique (MGT) as a function of the frequency difference between the interfering beams, obtained with a numerical simulation of undoped a-Si:H. The solid line corresponds to the exact value obtained with MGT, while the dotted lines were obtained using Eq. 6 with $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$ calculated for A_pp = π, 2π and 3π, as indicated in the caption

These figures allow testing the validity ranges of Eq. 6; for the different oscillation amplitudes, it is observed that the equality is strictly verified only in the region of low ∆ω. However, this region of low frequencies where Eq. 6 is verified becomes larger as the oscillation amplitude of the phase is increased. For A_pp = 3π (Fig. 4), it is observed just a slight mismatch at the highest frequencies; thus, in this case OPG is an acceptable approximation of MGT in the whole range of ∆ω values that can be achieved experimentally (up to $\sim {10}^{7}$ s⁻¹). More precision can be gained by increasing more the value of A_pp. These results are in accordance with the analysis performed in Sect. 2, according to which Eq. 6 should only be valid for values of Γ much greater than the duration of the transitory τ_t. By rewriting Eq. 5, the following condition for the validity of Eq. 6 is obtained,

$${\varGamma} = \frac{{2A_{pp} }}{{\left| {\Delta \omega } \right|}} \gg \tau_{t} .$$

(17)

If we assume that the time ${\tau }_{t}$ does not depend on A_pp and $\left| {\Delta \omega } \right|$, we see that the range of validity of Eq. 6 is given by $\left| {\Delta \omega } \right| \ll 2A_{pp} /\tau_{t}$, where it is observed that the range increases with the oscillation amplitude of the phase${A}_{pp}$, as obtained in the simulations.

For sufficiently large values of $\left| {\Delta \omega } \right|$ (high speeds of the IP), Eq. 6 overestimates the value of $\left| {\Delta J_{MGT} } \right|$. However, for the two smallest oscillation amplitudes in a region of intermediate $\left| {\Delta \omega } \right|$ values, it is observed a new behaviour that is not seen for the other oscillation amplitudes: the current density obtained with Eq. 6 underestimates the exact value. Thus, the shape of the transient current, produced after the sudden change of the IP velocity, depends on the amplitude of oscillation.

The difference between the angular frequencies of the interfering beams that induces the highest steady-state current in MGT, ∆ω_m, corresponds to the value of ∆ω for which the maximum occurs in the solid lines of Figs. 3 and 4. When OPG is used to obtain $\left| {\Delta J_{MGT} } \right|$, it is observed that the value of ∆ω_m is overestimated except for the smallest oscillation amplitude considered (A_pp = π/A). This behaviour is independent of the particular values of T, G₀ and $\Lambda$ chosen, except for the smallest amplitude of oscillation, which sometimes underestimates and sometimes overestimates the value of ∆ω_m. If Witt's formula, $\tau^{\prime} = \Delta \omega_{m}^{ - 1}$, is used as in [5, 6], τʹ would be usually underestimated and in the same proportion by which ∆ω_m is overestimated. Figure 5 presents the relative errors obtained for ∆ω_m at different temperatures, when ∆ω_m is obtained from $\left| {\Delta J_{OPG}^{{\omega_{o} }} } \right|$ for the three largest amplitudes of oscillation considered here (A_pp = π, 2π and 3π). As expected, the errors are smaller as the oscillation amplitude of the phase is greater. For A_pp = π, the errors are between 45 and 280%. When the oscillation amplitude doubles (A_pp = 2π) the errors are drastically reduced; now being between 7 and 18%. For the greatest amplitude of oscillation considered (A_pp = 3π), the errors are between 4 and 10%. The points plotted in Fig. 5 were obtained with G₀ = 10²⁰ cm⁻³ s⁻¹ and$\Lambda$= 6 × 10^–4 cm, although the same trend was observed for other values of these parameters.

Fig. 5

${\Delta \omega }_{m}$ is the difference between the angular frequencies of the interfering beams in MGT that induces the highest current for certain T, G₀ and $\Lambda$ values. The figure presents the relative errors obtained for ∆ω_m by means of a numerical simulation of a-Si:H, when the current induced by MGT versus ∆ω is obtained from Eq. 6 and the current induced by OPG. The errors are always positive because OPG overestimates the value of ∆ω_m for these amplitudes of oscillation

In appendix B, we present a formal general proof of the tendencies observed here for values of A_pp multiples of π. We show that this behaviour does neither depend on the values of the material parameters nor on the rest of the experimental parameters.

5 Experimental procedure

To test the new theoretical results, we made measurements on the same undoped a-Si:H sample, 490-nm-thick, used in Ref. [7]. We measured the current induced at the fundamental frequency with OPG for A_pp = 3π/4, π/2 and π/4 at room temperature and $\Lambda$= 2 × 10^–4 cm. The experimental configuration used for OPG was presented in Fig. 1. As a light source, we used a linearly polarized He–Ne laser (633 nm/1.96 eV) because its photon energy is slightly greater than the mobility gap of device-quality a-Si:H (1.8 eV). The beams’ diameters on the sample (5 mm) were much larger than the separation between the electrical contacts (1 mm), to ensure the spatial uniformity of the illumination produced by each beam in the direction of the electrical current [14].

To modulate the phase of the weak beam, we used a linear low voltage electro-optical modulator (Quantum Technology, model 28, series M00-251). The electro-optic modulator (EOM) acts as a phase modulator only when one of its main axes coincides with the polarization direction of the incident light beam, as explained in Fig. 6. A more detailed description of the linear electro-optical modulator is presented in Appendix C. The photon flux was measured with a calibrated silicon photodiode, while the rest of the parameters necessary for the estimation of the generation rate in the material were obtained from the reflectance and transmittance spectrum (400–1750 nm).

Fig. 6

The perpendicular dotted lines correspond to the main directions of the electro-optic modulator (EOM), while the solid arrow corresponds to the direction of polarization of the incident light beam. In a the EOM acts as a phase modulator of the incident beam, while in b it acts as a polarization modulator of the incident beam. The change of phase or polarization of the incident light beam, are proportional to the voltage applied to the modulator

To observe large differences between the currents induced by OPG and MGT (especially for A_pp = 3π/4 and π/2) it is reasonable to make measurements for frequency differences between beams greater or equal than ∆ω_m (see Fig. 3). It is known that ∆ω_m increases with the generation rate [5]. The lock-in amplifier that we have (Stanford Research SR830) can only measure up to 102 kHz, thus to measure the current induced by OPG in the region near ∆ω_m we had to use a sufficiently small photon flux of 7 × 10¹⁴ cm⁻² s⁻¹, producing an average generation rate of 4 × 10¹⁸ cm⁻³ s⁻¹ into the sample. The intensity of the weak beam was set at a value approximately 10 times lower than that of the strong beam.

Before measuring the current induced by OPG, it was necessary to calibrate the amplitude of the weak beam’s phase oscillation introduced by the modulator, which is proportional to the amplitude of the input triangular signal produced with a wave generator (see Fig. 1). The most direct way to perform the calibration would be by measuring the oscillation amplitude of the interference pattern, for which it would be necessary to focus the interference pattern on a screen after amplifying it with a lens; although, we use the simpler indirect way described below.

The EOM is initially rotated to act as a polarization modulator of the incident beam. In this case, the main axes of the modulator are at 45° from the direction of polarization of the incident beam (see Fig. 6b). Additionally, a linear polarizer is placed at the output of the modulator, which only lets pass the light polarized in the initial direction of polarization (or equivalently in the perpendicular direction, as we show below). The resulting intensity is measured with a fast photodiode. The fluxes of photons polarized in these directions are given, respectively by:

$$F_{\parallel } = \frac{{F_{T} }}{2}\left[ {1 + \cos \left( {2\varphi \left( t \right)} \right)} \right], F_{ \bot } = \frac{{F_{T} }}{2}\left[ {1 - \cos \left( {2\varphi \left( t \right)} \right)} \right] = F_{T} - F_{\parallel } ,$$

(18)

where F_T is the total flux of photons, $F_{T} = F_{\parallel } + F_{ \bot }$. By replacing Eq. 1 into Eq. 18, the theoretical time dependence of the output light intensities ($F_{\parallel }$ and $F_{ \bot }$) are obtained. Figure 7 presents the exit light intensity in the perpendicular direction, for the three measured amplitudes of oscillation. The parallel intensity component has exactly the same shape but is displaced half period. Note that the intensities ($F_{\parallel }$ or $F_{ \bot }$) depend strongly on the amplitude of oscillation. Therefore, it is possible to determine precisely the oscillation amplitude of the phase (A_pp) by observing with an oscilloscope the electrical signal induced by the parallel or perpendicular light component in a photodiode. In this case, the system integrated by the EOM and the linear polarizer act as an intensity modulator for the incident light beam.

Fig. 7

Modulated light intensity as a function of time, produced with the electro-optical modulator (EOM) acting as a polarization modulator and a linear polarizer placed subsequently, which only let pass the light polarized in the direction perpendicular to the initial one. The EOM is fed with triangular electrical signals of different amplitudes, A_pp = π/4, π/2 and 3π/4. It can be observed that the intensity of the linearly polarized light depends strongly on the amplitude of the input signal

For the correct determination of the current induced by OPG, it is also necessary to find out the sensitivity of the measurement system, to correct later the current values measured at different frequencies. For this purpose, the sample is replaced by a fast photodiode that is illuminated with an alternating illumination of variable frequency, whose intensity does not depends on the chosen frequency. The photocurrent of the fast photodiode is measured as a function of the frequency, using the same amplification factor as for OPG measurements. Figure 8 shows the resulting normalized photocurrent, where it can be seen that the higher the frequency, the lower the sensitivity of the measurement system. Correcting the current values measured by OPG with Fig. 8, the true current induced by OPG is obtained. The alternating illumination was produced by modulating the intensity of the HeNe laser light with the EOM and the linear polarizer, in the same way as for the oscillation amplitude calibration of the weak beam phase.

Fig. 8

Sensitivity of the measurement system as a function of frequency. The sensitivity decreases with the frequency of the input signal

6 Experimental results and discussion

Figure 9 presents the current density induced by the moving grating, $\left| {\Delta J_{MGT} } \right|$, as a function of the angular frequency difference between the interfering beams, $\left| {\Delta \omega } \right|$. These experimental results were obtained with OPG for three different oscillation amplitudes ($A_{pp} = \pi /4, \,\pi /2, \,3\pi /4$) and with MGT. While the values of $\left| {\Delta J_{MGT} } \right|$ vs. $\left| {\Delta \omega } \right|$ depend specifically on the sample and experimental conditions, such as temperature and generation rate, the qualitative relationships between the different curves are independent of these values (see Sect. 4). Note that the same trends obtained with the numerical simulation (Fig. 3) have been obtained experimentally (Fig. 9). As the amplitude of oscillation decreases in OPG the maximum current density shifts towards lower values of $\left| {\Delta \omega } \right|$ and decreases in magnitude (indicated by a dashed arrow in Figs. 3 and 9). The expected overestimation in the position of the maximum is clearly observed for the oscillation amplitudes 3π/4 and π/2. It can also be appreciated the expected superposition between OPG and MGT measurements for low enough $\left| {\Delta \omega } \right|$ values.

Fig. 9

Experimental steady-state current densities corresponding to the Moving photocarrier Grating Technique (MGT) as a function of the angular frequency difference between the interfering beams. The circles correspond to the exact values obtained with MGT, while the triangles were obtained using Eq. 6 and the current induced by OPG at the fundamental frequency for three different oscillation amplitudes, as indicated in the caption

It was impossible to achieve experimentally the ${A}_{pp}$ values required to verify the equivalence between MGT and OPG in the complete range of $\left| {\Delta \omega } \right|$ values, because our EOM saturates for values of $A_{pp} \cong 0.9 \times \pi$. However, having found the same trends and behaviour both experimentally and with the numerical simulations (at least for small oscillation amplitudes) gives support to the new theoretical results presented in this paper.

7 Conclusions

In this work, we carry out a thorough review of OPG technique, which was originally proposed as an AC implementation of MGT to increase the signal-to-noise ratio. Initially, we find the proportionality constant between the steady-state DC signal induced by MGT and the first harmonic component of the steady-state AC signal induced by OPG. Unlike in previous papers [1, 5, 6], the expression that we propose explicitly involves the oscillation amplitude of the phase (A_pp), and we argue that this relation would only be valid for low enough oscillation frequencies (ω₀). For the first time, we obtain the expression for the current density induced at the fundamental frequency by OPG using the multiple trapping model. Through a numerical simulation corresponding to undoped a-Si:H, it is observed that OPG and MGT currents are proportional only in the low IP speed region and that this region can be enlarged by increasing the value of A_pp. For a certain IP speed (i.e., ∆ω value), the oscillation frequency ω₀ can be reduced by increasing the IP oscillation amplitude (i.e., the A_pp value). An acceptable approximation of MGT current, in the entire range of measurable ∆ω values, is obtained with OPG for A_pp = 3π, which is six times greater than the previously used value [1, 5, 6].

The new theoretical results are tested experimentally only for the three smallest oscillation amplitudes evaluated with the numerical simulations (A_pp = 3π/4, π/2 and π/4) because the used EOM saturates for A_pp = 0.9 × π. A remarkable difference is observed between the values of $\left| {\Delta J_{MGT} } \right|$ vs. $\left| {\Delta \omega } \right|$ obtained directly with MGT and those obtained from OPG measurements for the different oscillation amplitudes. The same trends are obtained in the numerical simulation and in the measurements, validating the presented analysis. Despite the limitation of the used EOM, phase modulators capable of easily achieving the oscillation amplitudes needed to test the equivalence between OPG and MGT, in the entire range of measurable ∆ω values, are currently available on the market (see, for example, Ref. [15]). We encourage other researchers who have access to this kind of phase modulators to provide the final experimental proofs of the theoretical results presented.

Appendices

Appendix A

Deduction of the current density expression at the fundamental frequency

It is convenient to write the oscillation amplitude of the phase as A_pp = lπ, being l a positive number. It can be shown that when A_pp is a multiple of π (integer l), of the infinite terms that make up the generation rate (Eq. 7) no more than 6 influence the current induced at the fundamental frequency. These terms are given by:

$$g_{{ \pm \left( {l - 1} \right)\omega_{o} }} = \frac{{2lj\Delta G_{0} }}{{\pi \left( {2l - 1} \right)}},$$

(19)

$$g_{{ \pm l\omega_{o} }} = \frac{{\Delta G_{0} }}{2},$$

(20)

$$g_{{ \pm \left( {l + 1} \right)\omega_{o} }} = \frac{{ - 2lj\Delta G_{0} }}{{\pi \left( {2l + 1} \right)}}.$$

(21)

Note that for l = 1 there are only five terms since in Eq. 19 we have a single term g₀. When l is integer, the obtained complex amplitude of the average current density at the fundamental frequency is:

$$\Delta J_{OPG}^{{\omega_{o} }} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\Delta \sigma_{{l\omega_{o} }} \Delta \xi_{{\left( {l - 1} \right)\omega_{o} }}^{ *} + \Delta \sigma_{{ - l\omega_{o} }}^{*} \Delta \xi_{{ - \left( {l - 1} \right)\omega_{o} }} + \Delta \sigma_{{ - \left( {l - 1} \right)\omega_{o} }} \Delta \xi_{{ - l\omega_{o} }}^{ *} + \Delta \sigma_{{\left( {l - 1} \right)\omega_{o} }}^{*} \Delta \xi_{{l\omega_{o} }} } \\ { + \Delta \sigma_{{ - \left( {l + 1} \right)\omega_{o} }}^{*} \Delta \xi_{{ - l\omega_{o} }} + \Delta \sigma_{{\left( {l + 1} \right)\omega_{o} }} \Delta \xi_{{l\omega_{o} }}^{ *} + \Delta \sigma_{{l\omega_{o} }}^{*} \Delta \xi_{{\left( {l + 1} \right)\omega_{o} }} + \Delta \sigma_{{ - l\omega_{o} }} \Delta \xi_{{ - \left( {l + 1} \right)\omega_{o} }}^{ *} } \\ \end{array} } \right],$$

(22)

where the asterisk as superscript corresponds to the complex conjugation of the number. When ${\xi}_{ext}=0$, the symmetry between the generation rates ${g}_{\Omega}={g}_{-\Omega}$ implies the following relationships for the conductivity and the electric field amplitudes:

$$\Delta \sigma_{ - \Omega } = \frac{{g_{\Omega } }}{{g_{\Omega }^{*} }}\Delta \sigma_{\Omega }^{*} , \Delta \xi_{ - \Omega } = - \frac{{g_{\Omega } }}{{g_{\Omega }^{*} }}\Delta \xi_{\Omega }^{ *} .$$

(23)

In this case, Eq. 22 simplifies to:

$$ \begin{aligned}\Delta J_{OPG}^{{\omega_{o} }} &= \Delta \sigma_{{l\omega_{o} }} \Delta \xi_{{\left( {l - 1} \right)\omega_{o} }}^{ *} + \Delta \sigma_{{\left( {l - 1} \right)\omega_{o} }}^{*} \Delta \xi_{{l\omega_{o} }}\\ &\quad + \Delta \sigma_{{\left( {l + 1} \right)\omega_{o} }} \Delta \xi_{{l\omega_{o} }}^{ *} + \Delta \sigma_{{l\omega_{o} }}^{*} \Delta \xi_{{\left( {l + 1} \right)\omega_{o} }} .\end{aligned} $$

(24)

Note that under these circumstances, we only need to solve the general equations for three traveling waves with different values of Ω to obtain the current density induced at the fundamental frequency.

When A_pp is not a multiple of π (l is not an integer), the expression for the amplitude of the average current density induced at the fundamental frequency has infinite terms and is given by

$$ \begin{aligned}\Delta {J}_{OPG}^{{\omega }_{o}}&=\frac{1}{2}\sum_{i=1}^{\infty }\left[\Delta {\sigma }_{i{\omega }_{o}}\Delta {\xi}_{\left(i-1\right){\omega }_{o}}^{ *}+\Delta {\sigma }_{-i{\omega }_{o}}^{*}\Delta {\xi}_{\left(1-i\right){\omega }_{o}}\right.\\&\quad \left.+\Delta {\sigma }_{\left(1-i\right){\omega }_{o}}\Delta {\xi}_{-i{\omega }_{o}}^{ *}+\Delta {\sigma }_{\left(i-1\right){\omega }_{o}}^{*}\Delta {\xi}_{i{\omega }_{o}}\right].\end{aligned} $$

(25)

For A_pp = 3π/4, π/2 and π/4, the harmonic terms’ amplitudes of the generation rate are, respectively, given by:

$$g_{{ \pm i\omega_{o} }}^{l = 3/4} = \frac{{3\left( { - 1} \right)^{i} \Delta G_{0} }}{{\pi \sqrt 2 \left( {\frac{9}{4} - 4i^{2} } \right)}}\left( {1 + j\left( {1 + \left( { - 1} \right)^{i} \sqrt 2 } \right)} \right),$$

(26)

$$g_{{ \pm \left( {2i + 1} \right)\omega_{o} }}^{l = 1/2} = \frac{{2\sqrt 2 \Delta G_{0} }}{{\left( {4\left( {2i + 1} \right)^{2} - 1} \right)\pi }} , g_{{ \pm 2i\omega_{o} }}^{l = 1/2} = \frac{{ - j2\sqrt 2 \Delta G_{0} }}{{\left( {4\left( {2i} \right)^{2} - 1} \right)\pi }},$$

(27)

$$g_{{ \pm i\omega_{o} }}^{l = 1/4} = \frac{{\Delta G_{0} }}{{8\pi \left( {\frac{1}{16} - i^{2} } \right)}}\left( {\sqrt 2 \left( { - 1} \right)^{i} + j\left( {2 - \sqrt 2 \left( { - 1} \right)^{i} } \right)} \right),$$

(28)

where i = 0, 1, 2, ⋯. In these cases, is also verified that g_Ω = g_-Ω; therefore, in the absence of an external electric field (ξ_ext = 0), Eq. 23 are also verified. With these simplifications Eq. 25 reduces to:

$$ \begin{aligned}\Delta J_{OPG}^{{\omega_{o} }} &= \frac{1}{2}\sum_{i = 1}^{\infty } {\left( {1 - \frac{{g_{{i\omega_{o} }}^{*} g_{{\left( {i - 1} \right)\omega_{o} }} }}{{g_{{i\omega_{o} }} g_{{\left( {i - 1} \right)\omega_{o} }}^{*} }}} \right)}\\&\quad{\left( {\Delta \sigma_{{i\omega_{o} }} \Delta \xi_{{\left( {i - 1} \right)\omega_{o} }}^{ *} + \Delta \sigma_{{\left( {i - 1} \right)\omega_{o} }}^{*} \Delta \xi_{{i\omega_{o} }} } \right)} .\end{aligned} $$

(29)

Appendix B

Equivalence between MGT and OPG for A _pp multiple of ${\varvec{\pi}}$

In this appendix, we prove, for A_pp multiple of π, that Eq. 6 is strictly verified in the linear region of small frequencies. In the high-frequency regime we show that, the better the inequality A_pp ≫ π is fulfilled, the better Eq. 6 is satisfied.

In appendix A of Ref. [7] are solved the general transport equations for a generation rate consisting of an arbitrary harmonic travelling wave on a much greater uniform background. The harmonic amplitudes of the photoconductivity and electric field can be rewritten in the following way:

$$\Delta \sigma_{\Omega } = g_{\Omega } \Delta \sigma_{\Omega }^{0} , \quad \Delta \xi_{\Omega } = g_{\Omega } \Delta \xi_{\Omega }^{ 0} ,$$

(30)

where $\Delta \sigma_{\Omega }^{0}$ and $\Delta \xi_{\Omega }^{0}$ do not depends on the harmonic amplitude of the generation rate, g_Ω. The first-order Taylor expansion of $\Delta \sigma_{\Omega }^{0}$ and $\Delta \xi_{\Omega }^{0}$ at Ω = 0 are:

$$\Delta \sigma_{\Omega }^{0} \approx \Delta \sigma_{0}^{0} + \left( {\Delta \sigma_{0}^{0} } \right)^{\prime } \Omega , \Delta \xi_{\Omega }^{ 0} \approx \Delta \xi_{0}^{ 0} + \left( {\Delta \xi_{0}^{ 0} } \right)^{\prime } \Omega ,$$

(31)

where $\Delta \sigma_{0}^{0}$ and $\left( {\Delta \xi_{0}^{0} } \right)^{\prime }$ are real numbers, while $\left( {\Delta \sigma_{0}^{0} } \right)^{\prime }$ and $\Delta \xi_{0}^{0}$ are imaginary. Replacing Eqs. 30 in the expression of the MGT current density [7], it is obtained:

$$\Delta J_{MGT} = \frac{{\Delta G_{0}^{2} }}{2}Re\left\{ {\Delta \sigma_{\Delta \omega }^{0} \left( {\Delta \xi_{\Delta \omega }^{ 0} } \right)^{*} } \right\}.$$

(32)

Substituting Eqs. 31 in Eq. 32, discarding the higher-order terms and after some algebra, we get the expression of MGT current density in the low-frequency region:

$$\Delta J_{MGT} \approx \frac{{\Delta G_{0}^{2} }}{2}\Delta \omega \left[ {\Delta \sigma_{0}^{0} \left( {\Delta \xi_{0}^{ 0} } \right)^{\prime } - \left( {\Delta \sigma_{0}^{0} } \right)^{\prime } \Delta \xi_{0}^{ 0} } \right].$$

(33)

Replacing Eq. 30 in Eq. 24 and using Eqs. 19–21, we obtain the following formula for the current density induced by OPG at the fundamental frequency when A_pp is a multiple of π:

$$ \begin{aligned}\Delta J_{OPG}^{{\omega_{0} }} &= \frac{{ - lj\Delta G_{0}^{2} }}{\pi }\left[ {\frac{{\Delta \sigma_{{l\omega_{0} }}^{0} \left( {\Delta \xi_{{\left( {l - 1} \right)\omega_{0} }}^{ 0} } \right)^{*} + \left( {\Delta \sigma_{{\left( {l - 1} \right)\omega_{0} }}^{0} } \right)^{*} \Delta \xi_{{l\omega_{0} }}^{ 0} }}{{\left( {2l - 1} \right)}} }\right.\\&\qquad\qquad\left.{+ \frac{{\Delta \sigma_{{\left( {l + 1} \right)\omega_{0} }}^{0} \left( {\Delta \xi_{{l\omega_{0} }}^{ 0} } \right)^{*} + \left( {\Delta \sigma_{{l\omega_{0} }}^{0} } \right)^{*} \Delta \xi_{{\left( {l + 1} \right)\omega_{0} }}^{ 0} }}{{\left( {2l + 1} \right)}}} \right].\end{aligned} $$

(34)

Substituting Eqs. 31 in 34, dismissing the higher-order terms and after some algebra we get the equation for OPG current density in the low-frequency region:

$$\Delta J_{OPG}^{{\omega_{0} }} \approx \frac{{ - 2l\omega_{0} j\Delta G_{0}^{2} }}{\pi }\left[ {\Delta \sigma_{0}^{0} \left( {\Delta \xi_{0}^{ 0} } \right)^{\prime } - \left( {\Delta \sigma_{0}^{0} } \right)^{\prime } \Delta \xi_{0}^{ 0} } \right].$$

(35)

Taking the modulus of Eqs. 33 and 35, and using the relationship $\left| {\Delta \omega } \right| = l\omega_{0}$, we obtain Eq. 6.

The inequality A_pp ≫ π is equivalent to l ≫ 1. Discarding the $1$ in front of $l$ and $2l$ in Eq. 34, we get the formula of OPG current density in this case:

$$\Delta J_{OPG}^{{\omega_{0} }} = \frac{{ - j2\Delta G_{0}^{2} }}{\pi }Re\left\{ {\Delta \sigma_{{l\omega_{0} }}^{0} \left( {\Delta \xi_{{l\omega_{0} }}^{ 0} } \right)^{*} } \right\}.$$

(36)

Taking the modulus of Eqs. 32 and 36 and assuming $\left| {\Delta \omega } \right| = l\omega_{0}$, we get Eq. 6. Note that the inequality A_pp ≫ π or l ≫ 1, is also equivalent to a maximum displacement of the interference pattern much greater than half its spatial period (D_pp ≫ $\Lambda$/2).

Appendix C

Electro-optic modulator (EOM)

In a typical linear EOM, the refractive indexes in the main directions of the active crystal (perpendicular to each other) are directly proportional to the applied voltage. The proportionality constant is the same in both directions, although of opposite signs. In the absence of voltage applied to the modulator, a linearly polarized beam of light retains its initial polarization because the refractive indices are equal in both directions. Therefore, its electric field written in the main directions of the modulator is,

$$\vec{E} = E_{0} \cos (\theta )\cos (kz - \omega t)\hat{\text{x}} + E_{0} \sin (\theta )\cos (kz - \omega t)\hat{\text{y}},$$

(37)

where θ is the angle that forms the electric field of the incident beam with the main direction ${\hat{\text{x}}}$ of the EOM. By applying a potential difference to the modulator, there is an increase in the optical path for polarized light in one main direction and a decrease in the optical path of the same magnitude for polarized light in the other main direction. In this case, the electric field of the light beam at the output of the modulator is,

$$ \begin{aligned}\vec{E} &= \,E_{0} \cos \left( \theta \right)\cos \left( {kz - \omega t + \varphi \left( V \right)} \right){\hat{\text{x}}} \\&\quad+ E_{0} \sin \left( \theta \right)\cos \left( {kz - \omega t - \varphi \left( V \right)} \right){\hat{\text{y}}},\end{aligned} $$

(38)

Note that the EOM acts as a phase modulator of the light beam only when one of its main axes coincides with the direction of polarization of the incident light beam. On the other hand, the EOM acts as a polarization modulator capable of rotating 90° the initial direction of polarization only when the main axes of the modulator are at 45° from the polarization of the incoming light beam. In this case, Eq. 38 becomes,

$$\vec{E} = \frac{{E_{0} }}{\sqrt 2 }\cos \left( {kz - \omega t + \varphi \left( V \right)} \right){\hat{\text{x}}} + \frac{{E_{0} }}{\sqrt 2 }\cos \left( {kz - \omega t - \varphi \left( V \right)} \right){\hat{\text{y}}}{.}$$

(39)

When φ (V) = π/4, for example, we obtain a circularly polarized light at the output of the modulator, and for φ (V) = π/2 we obtain again linearly polarized light but rotated 90 degrees from the input direction of polarization.