1 Introduction

Structured light is a highly topical field due to the existence of a modern toolkit to create such tailored fields and the many applications that it has fostered [1,2,3,4]. A particularly well-studied example is the self-healing property of some light beams, first observed for Bessel beams in the late nineties [5]. Since then, there have been numerous studies, not only on Bessel beams [6,7,8,9] but also on a myriad of other structured light fields, including Airy [10], Caustic optical [11], Weber and Mathieu [12], Hermite-Gaussian (HG) and Ince–Gaussian [13] beams, as well as angular self-healing of orbital angular momentum (OAM) beams [14], polarization self-healing of vector beams [15, 16], and even the recovery of entanglement in quantum states [17, 18]. There is a good reason for the extensive studies that persist even today: self-healing beams have found numerous applications, including multiple plane micro-manipulation [19], robust optical communication [20], reduced scattering in imaging microscopy [21], enhanced laser machining [22], and quantum key distribution through obstacles [17, 18]. In parallel to the experimental observations, and considering the counter-intuitive nature of self-healing, researchers have spared no efforts in attempting to explain why certain classes of optical modes self-heal. Presently, these include both geometric [6, 23,24,25] and wave [26,27,28,29] arguments. Self-healing has also been related to the spatial filtering concept [30], but the argument has not been elaborated on. Intriguing is the prediction that radial mode Laguerre–Gaussian (LG) beams would also self-heal [31], suggesting that the reason self-healing is not observed in OAM beams is the missing ring-like structure of the radial modes. The argument is based on the mathematical similarity of LG modes to Bessel modes, with similar arguments holding for HG modes [32].

In this paper, we study the self-healing properties of LG beams and explain our findings by investigating two types of circular obstructions: an aperture, in which the outer part of the beam is blocked, and an opaque disk, in which the central part of the beam is blocked. We extend the usual treatment of intensity self-healing to consider recovery of salient propagation features, specifically, beam width, beam divergence, and the beam propagation factor, \(M^2\). We based our study on two key parameters: (1) the focal shift effect and (2) the beam propagation factor, \(M^2\). The former arises when an optical beam is focused by a lens, or truncated by an obstacle, and the usual geometric focal plane shifts toward the incoming beam, where the amount of the focal shift is strongly related to the focusing lens or to the obstacle size [33,34,35,36,37,38]. The latter is strongly related to aberrations and diffraction effects [39,40,41,42,43,44,45,46,47,48], affecting the overall propagation characteristics of the beam. To achieve this, we perform a full theoretical and experimental study to monitor the self-healing, through measuring transverse and axial intensities, focal plane shifts, beam radius, and beam quality factor \(M^2\), and demonstrate that the type of obstruction significantly influences the beam’s features. Furthermore, by borrowing concepts from image analysis, not usually associated with self-healing of structured light, to explain the observations by acknowledging the obstructed beam’s spatial frequencies and its modulation by the obstacles. Our work therefore not only provides important experimental validation but also offers a new interpretation that establishes a self-healing regime. This holistic study will be of benefit to the large community wishing to exploit such structured light fields.

2 Concept and numerical predictions

In this section, we introduce the optical system under study, outline the concept to evaluate the self-healing of radial LG beams, and numerically simulate the effects to be studied experimentally.

To begin, consider a cylindrical LG beam with radial index p:

$$\begin{aligned} u_\text {in}(\rho , z=0) \propto L_{p}\left( 2\frac{\rho ^2}{w^2(z)}\right) \exp \left( -\frac{\rho ^2}{w^2(z)}\right) , \end{aligned}$$
(1)

where \(w^2(z)=w_0^2[1+(z/z_\text {R})^2]\) is the beam width, \(z_R=\pi w_0^2/\lambda \) is the Rayleigh length, \(w_0\) is the Gaussian waist radius, and \(L_{p}\) is a Laguerre polynomial of order p. We imagine this beam incident on two obstructions (an aperture and an opaque disk) characterized by transmittance functions:

$$\begin{aligned} \tau _\text {AP}(\rho )= {\left\{ \begin{array}{ll} 1 &{} \rho \le a\\ 0 &{} \rho > a \end{array}\right. }, \end{aligned}$$
(2)

and

$$\begin{aligned} \tau _\text {OD}(\rho )= {\left\{ \begin{array}{ll} 0 &{} \rho \le a\\ 1 &{} \rho > a \end{array}\right. }, \end{aligned}$$
(3)

with a the radius of the obstruction for the aperture (AP) and opaque disk (OD), respectively.

To examine the effect of the aperture and the opaque disk on the LG beam propagation, we simulated the optical system, as shown in Fig. 1. We considered the incident electric field with amplitude \(u_\text {in}(\rho , z=0)\) impinging upon a lens and an obstruction, both at \(z=0\), and numerically solve the Fresnel–Kirchhoff diffraction integral in cylindrical coordinates to compute the propagated field. Due to the azimuthal symmetry of the LG beams, both types of apertures are circular structures and are thus characterized by their radii. In the case of the aperture, this corresponds to the radius of the hole, and in the case of the opaque disk, to the radius of the obstruction itself. In all cases, radii were chosen to coincide with the zeros of the beam’s intensity. The motivation for this is to keep the disturbance of spatial frequencies to a minimum, acting as a filter for some predetermined number of rings, or equivalently, some predetermined spatial frequencies. We are interested in the propagation of the beam after the lens, particularly at the Fourier plane (\(z=f\)), and the so-called shifted plane at \(z=z_0\). In this work, the shifted plane is defined as the plane corresponding to the position of minimum beam width, that is, the waist position of the distorted beam. Both planes are shown in Fig. 1 as dashed vertical lines.

The concept which we adopted in this work to evaluate the self-healing of the LG beam (which is valid for any beam belonging to scaled propagation invariant beams) is based on two effects: the first is the evaluation of the self-reconstruction of the beam’s intensity profile, and the second is the evaluation of the recovery (conservation) of well-known beam characteristics such as the beam propagation factor, \(M^2\), and the focal shift effect. This holistic approach for assessing the self-healing will significantly help to justify the physical interpretation which we introduce based on spatial frequency filtering following Abbe.

Fig. 1
figure 1

Conceptualization of the system under study, with the initial radial LG beam passing through a an aperture and b an opaque disk, and then focussed with a lens. The incident beam is partially blocked at the lens plane (\(z=0\)) by an obstruction of some radius, selected to coincide with the zeros of the initial beam. The output beam is interrogated both at the geometrical focal plane (Fourier plane) of the lens and at the shifted focal plane (shifted plane in short), which corresponds to the plane where the second moment width of the output beam is minimum

Full size image

From the Fresnel–Kirchhoff diffraction theory, the propagated electric field at a distance z is given by [49, 50]:

$$u_{{{\text{out}}}} (r,z) = \int_{0}^{\infty } {u_{{{\text{in}}}} } (\rho ,z = 0)\tau (\rho )J_{0} \left( {\frac{{2\pi }}{{\lambda z}}r\rho } \right)\exp \left[ {\frac{{i\pi \rho ^{2} }}{\lambda }\left( {\frac{1}{z} - \frac{1}{f}} \right)} \right]\rho {\text{d}}\rho, $$
(4)

where r is the radial distance to the propagation axis and \(J_{0}\) is the Bessel function of order zero.

Figure 2 shows density plots in the xz-plane of the propagated beam for unobstructed (Fig. 2a), obstructed by an aperture (Fig. 2b) and obstructed by an opaque disk (Fig. 2c). The vertical axis corresponds to the transverse x-axis, normalized to the beam’s Gaussian waist (\(w_0\)), while the horizontal axis is the propagation z-axis, normalized to the focal length, f. For all images, the Fourier plane is marked by a vertical blue dotted line. The bottom panels present the transverse intensity profiles at the shifted plane \(z=z_0\), where the unobstructed beam is shown in black and the obstructed one in red. By comparing Fig. 2a–c, it can be seen that while the beam shape and width are significantly affected by the aperture, the beam is scarcely modified by the opaque disk at the shifted plane. This is further illustrated in the intensity profiles, where it is seen that the beam recovers its shape only when obstructed by an opaque disk. This constitutes a clear indication that the type of obstruction greatly influences the effect it has on the beam.

Fig. 2
figure 2

Numerical simulation for an LG\(_{50}\) beam. Density plots in the xz-plane (top row) and profiles along the x-axis (bottom row) of the intensity distribution of the beam for a an unobstructed beam, the beam after passing through b an aperture, and c an opaque disk

Full size image

Spatial filtering [51, 52] is used in this paper to qualitatively explain the physics behind the self-healing of LG beams. We remind the reader of Ernst Abbe’s observations on image formation, where he found that the resolution of the image depends on the number of spatial frequencies that are passed through the imaging system [53]. Based on this, in the image processing context, it is customary to perform spatial filtering by removing specific frequency ranges. For instance, a low-pass filter will reduce high-frequency noise and has an overall “smoothing” effect, while a high-pass filter will emphasize fine details in the image and enhance edges. We now consider this in the context of structured light rather than imaging. The spatial filtering process allows us to hypothesize that the bulk of the beam’s information is found in the high-frequency content, that is, in the outermost region. This implies that removing this spatial frequency content will have a stronger effect on the beam in comparison to removing the lower frequency content. In other words, an obstruction of the higher frequencies (an aperture) will have a severe impact on the beam, while obstruction of the lower frequencies (an opaque disk) will have less of an effect. This is precisely the behavior we observe in the numerical simulations in Fig. 2.

3 Experimental setup

To experimentally confirm our numerical predictions, we used the experimental setup shown schematically in Fig. 3. Light from a He–Ne laser operating at a wavelength of \(\lambda =632.8\) nm was expanded and collimated using a telescope (lenses L1, \(f_1=50\) mm, and L2, \(f_2=500\) mm) for illumination of a phase-only spatial light modulator (SLM—HOLOEYE PLUTO) displaying a computer-generated hologram (CGH). The CGHs were created by complex amplitude modulation [54, 55] and designed to simultaneously encode the LG beam, the lens (\(f=250\) mm), and the obstruction (aperture or opaque disk). A 4f system (lenses L3, \(f_3=250\) mm, and L4, \(f_4=250\) mm) imaged the SLM plane to the back focal plane of lens L4, and simultaneously filtered out unwanted diffraction orders with an iris at the Fourier plane of L3. Finally, a CCD camera (Point Grey Firefly) was mounted onto a guiding rail along the propagation axis to obtain a series of images of the beam intensity at different propagation distances. Crucially, encoding the lens into the hologram enabled us to measure the beam intensity near \(z=0\) without any physical limitation.

Fig. 3
figure 3

Schematic of the experimental setup used to study the self-healing ability of an LG beam (p = 5) obstructed by an aperture or an opaque disk. The SLM simultaneously generates the obstructed beam and encodes the lens

Full size image

4 Results

To study the self-healing process of LG beams, illustrative examples of the intensity patterns and their profiles for the obstructed LG beam of order \(p=5\) are presented in this section.

With the aim of having a reference point to compare the obstructed beams against, we start by showing the beam intensity of the unobstructed beam at the shifted (Fig. 4a) and Fourier (Fig. 4b) planes. It can be seen they are very similar, since, in this particular case, the above-mentioned planes are very near to each other (Fig. 2a).

Fig. 4
figure 4

Experimental and theoretical (insets) intensity patterns and the corresponding cross-sectional profiles for non-obstructed LG beam of order \(p=5\), at a the shifted plane and b the geometric focal plane (Fourier plane)

Full size image

We begin with an LG beam of order \(p=5\) as an illustrative example and consider the conventional intensity profile self-healing. Results of the experiment for the aperture are shown in Fig. 5 at both the shifted (top row) and Fourier (bottom row) planes, for three different aperture radii. It is worth noting that the position of the shifted plane strongly depends on the aperture size; therefore, the specific value for \(z_0\) is different for each case. The insets show the corresponding theoretical predictions to experimental measurements. While below each image, we show the cross-sectional intensity profile.

Fig. 5
figure 5

Experimental and theoretical (insets) intensity patterns (density plots) and the corresponding cross-sectional profiles in the panels below. Shown here are results at the shifted plane for an obstructed LG\(_{50}\) beam by an aperture at a its second intensity zero, b third intensity zero, and c fifth intensity zero. The equivalent results at the Fourier plane are shown in panels d–f, respectively

Full size image

One notices that the obstructed intensity patterns differ from the unobstructed ones, particularly when a large portion of the beam is blocked. The beam never recovers its initial profile at any plane, even in the far field, revealing that the beam does not self-heal after it is blocked by an aperture.

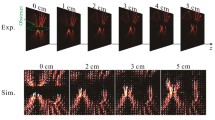
In contrast to this is the more conventional case of obstruction by an opaque disk, with experimental results shown in Fig. 6. The intensity distributions are shown at a plane just after the opaque disk \(z=10\) mm, and at the shifted plane \(z=z_0\); note that, for these beam parameters, the Fourier plane and the shifted plane are very close and, therefore, their intensity patterns are almost identical; hence, we only show the intensity at the shifted plane. As before, we used an LG beam of order \(p=5\) and the opaque disks blocked the beam up to its second, third, and fifth intensity zeros (counting from the beam’s center). Figure 6a–c clearly shows the effect of the opaque disk on the beam in the near-field, in such a way that the inner rings “disappear” as the disk radius increases, as one would expect. On the other hand, comparing the unobstructed beam from Fig. 4 against the blocked beam in Fig. 6d–f, it can be seen that the blocked part is reconstructed at the shifted plane in all examples. The reconstruction is almost perfect in the first case, good in the second, and discrepancies are more noticeable in the third. Nonetheless, considering the extent of the obstruction in the latter case, it is remarkable how similar the propagated beam is to the unobstructed one at the shifted plane.

As it is well known, it is worth noting the distance of the self-healing process depends on the opaque disk size, which means that the quality of the reconstructed beam in the second and the third case will be better after the shifted plane when the self-healing process is completed.

Fig. 6
figure 6

Experimental and theoretical (insets) intensity patterns and associated cross-sectional profiles in the near field \(z=10\) mm for an obstructed LG\(_{50}\) beam by an opaque disk at a its second intensity zero, b third intensity zero, and c fifth intensity zero. The equivalent results at the shifted planes are shown in panels d–f, respectively

Full size image

To quantify the reconstruction, we calculate the degree of similarity, which has been used extensively in the context of self-healing Bessel beams [28]. We follow this approach and define it as:

$$ S = \frac{{\int_{0}^{\infty } {\bar{u}_{{{\text{out}}}} } (r,z)u_{{{\text{out}}}}^{*} (r,z)r{\text{d}}r}}{{\sqrt {\int_{0}^{\infty } {\bar{u}_{{{\text{out}}}} } (r,z)\bar{u}_{{{\text{out}}}}^{*} (r,z)r{\text{d}}r} \sqrt {\int_{0}^{\infty } {u_{{{\text{out}}}} } (r,z)u_{{{\text{out}}}}^{*} (r,z)r{\text{d}}r} }}, $$
(5)

where \(\bar{u}_{{{\text{out}}}} (r,z)\) and \( u_{{{\text{out}}}} (r,z) \) denote the optical fields of the beam with and without obstruction, respectively, and \(u^*\) denotes the complex conjugate of u. Numerical simulations of Eq. (5) are shown in Fig. 7, where the similarity of both apertured and blocked LG\(_{50}\) beams are plotted at the plane \(z=z_{0}\), corresponding to the shifted plane of the unobstructed beam as a function of obstacle sizes. As seen from Fig. 7, the similarity degree for the blocked beam at the plane \(z=z_{0}\) decreases as the opaque disk size increases. While the similarity degree for the apertured beam at the same plane (\(z=z_{0}\)) increases with increasing of the aperture size.

Fig. 7
figure 7

Similarity, S, of both blocked (opaque disk) and apertured LG\(_{50}\) beams as function of the normalized obstruction size, \(a/w_0\). The red dots indicate the positions of the intensity zeros of the LG\(_{50}\) beam

Full size image

4.1 Beam propagation factor and the focal shift effect

The analysis of self-healing naturally involves propagation effects, but as with the previous section, these are typically intensity comparisons at specific planes. Here, we introduce a more quantitative analysis of the resulting propagation characteristics through the beam propagation factor, \(M^2\), and focal shift. Such parameters, particularly the former, are useful in predicting the beam’s performance for some application, and is a good indication of the brightness of the beam.

The \(M^2\) factor, sometimes called the beam quality factor or beam propagation factor, is an important parameter in describing the beam propagation features of a laser beam, encompassing both the beam width and its divergence into a single number, which in turn can be used to define the brightness of the beam, and how tightly it might be focused. It is easily calculated as [56, 57]:

$$\begin{aligned} M^2=\frac{\pi }{\lambda }w_r \theta _r, \end{aligned}$$
(6)

where the beam width, \(w_r\), and divergence, \(\theta _r\), are defined as second moments of the intensity [58, 59]:

$$ \langle w_{r}^{2} \rangle = \frac{{2\pi }}{{P_{0} }}\int_{0}^{\infty } \tau (\rho )|u_{{{\text{in}}}} (\rho ,0)|^{2} \rho ^{3} {\text{d}}\rho, $$
(7)
$$ \langle \theta _{r}^{2} \rangle = \frac{{2\pi }}{{k^{2} P_{0} }}\int_{0}^{\infty } \tau (\rho )|u^{\prime}_{{{\text{in}}}} (\rho ,0)|^{2} \rho {\text{d}}\rho + \frac{{32\pi }}{{3k^{2} P_{0} }}|u_{{{\text{in}}}} (a,0)|^{2} , $$
(8)

where \(P_0\) is the total power contained in the beam:

$$ P_{0} = 2\pi \int_{0}^{\infty } \tau (\rho )|u_{{{\text{in}}}} (\rho ,0)|^{2} \rho {\text{d}}\rho . $$
(9)

and \(u^{\prime}_{{{\text{in}}}} (\rho ,0)\) is the first derivative of the amplitude \(u_{{{\text{in}}}} (\rho ,0)\) of the LG beam at plane \(z=0\).

Based on Eqs. (6–8), we have derived the analytical expression for the \(M^2\) factor of an LG beam diffracted by an annular aperture as a general case, where the opaque disk and the aperture are particular cases. Because of the tedious calculation, here, only the obtained numerical results are presented.

Fig. 8
figure 8

The percentage change in a the beam quality factor and b focal shift of the obstructed beam as compared to the unobstructed beam, calculated as a function of the normalized obstruction size for an aperture and an opaque disk (blocked). All calculations assumed an initial LG\(_{50}\) beam with an \(M^2 = 2p +1\), \(\Delta z=z-z_0\) is the focal shift, and f is the focal length of the lens

Full size image

Figure 8 shows numerical simulations for the percentage change in \(M^2\), defined as \(\delta M^2=(M^2-(2p+1))/(2p+1)\), and the percentage change in the focal shift, defined as \(\Delta z/f=(z-z_0)/f \) for diffracted (apertured and blocked) LG\(_{50}\) beams as a function of the normalized obstruction parameter (the ratio of the obstacle size to the Gaussian waist, \(w_0\)). Not surprisingly, strongly apertured beams show a large change in \(M^2\), decreases steadily until the aperture is open and the beam is unperturbed. The beam’s propagation dynamics only recover when there is no obstruction. In contrast, the beam blocked by an opaque disk has an oscillatory response, with small changes near the zero’s of the LG\(_{50}\) intensity. This is supported by the experimental results, as shown in Fig. 6, where the LG\(_{50}\) beam almost recovers its shape for obstructions that allow at least two rings to bypass the disk. From the theory of perfect vortex beams, the Fourier transform of the remaining last ring using a lens is a Bessel–Gaussian beam [60,61,62], which is known to be approximate to an LG beam [31, 63]. These results are corroborated by the equivalent focal shift trends: the rate change of the focal shift for the blocked beam is negligible, while the rate change for the apertured beam is very high, confirming that the beam recovers against opaque disks but not against apertures.

As a first conclusion, it is confirmed theoretically and experimentally that the LG beam self-heals if the opaque disk lets some light (rings) bypass the obstruction, as has been predicted by alternative arguments previously [31]. By considering the outer rings as the higher spatial frequency components of the field, this result can be interpreted based on the spatial frequency filtering argument, that any high-pass filtered image can be reconstructed by the interference of the remaining non-filtered high frequencies. Or in the context of structured light: there is enough information in the higher spatial frequencies to reconstruct the entire field.

To confirm these numerical results, we measure the full propagation of the field along the z-axis to extract the \(M^2\) and focal shift parameters. We illustrate one such example in Fig. 9, measured for the test LG\(_{50}\) beam (apertured and blocked) on its third ring compared to the unobstructed one. From the experimental results, we can extract the \(M^2\) factor, the new waist location \(z_0\), and the new waist size \(w_0\) from [59, 64]:

$$ w^{2} (z) = w_{0}^{2} + M^{4} \frac{{\lambda ^{2} }}{{\pi ^{2} w_{0}^{2} }}(z - z_{0} )^{2} . $$
(10)

Figure 9 shows the measured and simulated beam radii, normalized to the Gaussian beam width, as a function of propagation distance, z, normalized to the focal length, for an unobstructed beam (Fig. 9a), an obstructed beam on its third intensity zero by an aperture (Fig. 9b), and an opaque disk (Fig. 9c). The predicted propagation is in agreement with the measured dynamics. The small difference (\(\approx 15\%\)) between the theoretical and experimental results in \(M^2\) is likely due to the sensitivity of the second moment measurement-to-background noise. We see that the shifted planes of the unobstructed beam and the blocked beam by an opaque disk lie very close to the Fourier plane \(z=f\), to within about \(4\%\). However, the apertured beam is significantly shifted. Specifically, the shifted plane of the obstructed beam by an aperture is located at a position somewhat close to the obstruction (aperture) plane. We can understand the physics of this by considering the Fresnel number, \(F=a^2/\lambda f\), of the system. In the truncated case, the aperture limits the beam size, so the Fresnel number changes with the aperture size, thus affecting the focal shift. However, for the blocked case with an opaque disk, the outer spatial beam extent remains unchanged and thus the Fresnel number remains unchanged. For that reason, the focal shift phenomenon in apertured beams is different from the traditional blocked cases studied hitherto.

These theoretical and experimental results confirm our concept towards the ability of a laser beam to recover its features when encountering opaque disks but not when encountering apertures.

Fig. 9
figure 9

Theoretical and experimental beam radius as a function of normalized propagation distance for a unobstructed, and obstructed by b an aperture, and c an opaque disk. In all cases, the initial beam was an LG\(_{50}\) obstructed at its third intensity zero. The measured and predicted \(M^2\) values are given in the insets

Full size image

5 Discussion and conclusions

In this work, we have studied the self-healing ability of radial LG beams, introducing the concept of assessing the beam propagation features and considering the nature of the obstacle from a high-pass filter to a low-pass filter. Our results have illustrated that the self-healing abilities of an LG beam are strongly dependent on the type of obstruction and less pronounced on its size. It is noticed that the LG beams are rather robust to the opaque disk radii, where attaining high-quality reconstruction even when a relatively large part of the beam is blocked. In addition, Figs. 8 and 9 indicate that the obstructed beam by an opaque disk keeps almost the same characteristics of the unobstructed beam, which is not the case when the beam is obstructed by an aperture. Altogether, our results show that an LG is more capable of self-healing when obstructed by an opaque disk, than when blocked by an aperture. Of course, there are still cases when using the aperture where the beam will self-heal, and cases when using the opaque disk where it will not, but, in general, the self-healing ability of the LG is higher for opaque disk obstructions.

It is worth noting that these concepts and procedures are applicable for all beams belonging to the propagation invariant family, such as Hermite–Gauss (HG) and Ince–Gauss (IG) beams. Moreover, we have adopted an elegant way to interpret physically the self-reconstruction of these beams based on the concept of spatial frequency filtering: the LG beams can be viewed as images and the different rings of the beam as the different spatial frequencies (since these beams are scaled propagation invariant). From this view, when the beam is blocked by an aperture, it loses its high-frequency information, and when it is blocked by an opaque disk, it loses its low-frequency information. Therefore, recalling the spatial filtering concept, this means that the beam is able to reconstruct itself only when its higher spatial frequency content is preserved.

These results could also be interpreted using the ray description jointly with the spatial frequency concept. The aperture blocks the more inclined outer rays (high frequencies), which are responsible for constructing the inner part of the beam. However, the passed inner rays construct the outer part of the beam as seen in Fig. 5. On the other hand, the opaque disk blocks the inner rays (low frequencies), which are responsible for constructing the outer part of the beam. However, the passed outer rays construct the inner part of the beam, as seen also in Fig. 6. In both cases, the obstructed part of the beam (rays) is cycling, and they are replaced by the unobstructed parts (rays) to partially self-heal the beam [25]. We hope that this study will inspire new approaches for investigating the self-healing ability of other structured light beams.