1 Introduction

It is well known that an external potential is extensively employed to control the dynamics of the optical beams in linear and nonlinear media. Especially in linear media, by introducing different potential, such as the linear potential [1,2,3,4], the parabolic potential [5,6,7,8], and the dynamic potential [9, 10], the manipulation of optical beams has attracted much attention all over the world. Among multitudinous potentials, the manipulation and dynamic control of beams via the parabolic potential in linear media have been widely reported. For example, phase transition of Airy beams [11, 12], periodic abruptly autofocusing and autodefocusing behavior of circular Airy beams [13], self-induced periodic interfering behavior of dual Airy beam [14], and propagation of the Pearcey Gaussian beams in a medium with a parabolic refractive index [15]. In 1997, Snyder and Mitchell proposed a nonlocal model [16], and the model can be simplified as the linear Schrödinger equation with a parabolic potential in linear regime. Inspired by the results of this research, a large number of intriguing experimental investigations have been reported [17,18,19], the results show that the parabolic potential in linear regime can be realized in strongly nonlocal media, such as nematic liquid crystals, lead glass, when the characteristic response length of the nonlocal media is much broader than the beamwidth. The experimental realization of the optical parabolic potential paves the way for studying the dynamic behavior of optical beams in optical parabolic potential, so the related results have been reported one after another [20,21,22,23]. Besides the application of the parabolic potential in the optical manipulation, the parabolic potential also plays an important role in Bose–Einstein condensates [24, 25].

In 2007, using Ansatz method, Zhang et al. derived the analytical solutions of the Gaussian beam with the initial phase-front curvature in strongly nonlocal medium [26]. Generally, the analytical solutions for Gaussian beams with different initial chirps in a parabolic potential are different. For the ansatz method, we must know the form of the analytical solutions. Therefore, it is complex in searching for the solutions. In 2015, other analytical method was first introduced to obtain the dynamic solution of Airy beam in a medium with a parabolic potential [11]. The greatest advantage of this method reported in [11] is that it is not necessary to know the form of the analytical solutions. Therefore, this analytical approach is more effective and direct in evaluating optical beams with the different chirp than ansatz method.

In this article, using the approach reported in [11], we analytically demonstrate the effects of initial chirp on the dynamics of the Gaussian beams in parabolic optical potentials. The analytical method is more effective in evaluating Gaussian beams with the linear chirp and the quadratic chirp, respectively, than ansatz method. The results show that the linear chirp of beam can induce a periodically oscillating behavior, and the oscillating amplitude is proportional to the linear chirp parameter. The quadratic chirp of beam can induce a periodically breathing behavior, and the evolution of beam’s peak and width depends on the depth of parabolic potential and the quadratic chirp parameter.

The rest of this article is structured as follows: the model and its propagation solution are presented in the next section. In Sects. 3 and 4, based on the linear Schrödinger equation with a parabolic potential, the analytical results describing the evolution of the Gaussian beam with chirp are presented, and the effects of initial chirp on the dynamics of the optical beam are discussed in detail. Finally, the main results of the article are summarized in Sect. 5.

2 The model and solution

Here, we consider the propagation dynamics of Gaussian beams in a parabolic optical potential, which can be described by the normalized one-dimensional linear Schrödinger equation [11, 14]:

$$\begin{aligned} i\frac{\partial \phi }{\partial z}+\frac{1}{2}\frac{\partial ^{2}}{\partial x^{2}}\phi \left( x,z\right) -\frac{1}{2}\alpha ^{2}x^{2}\phi \left( x,z\right) =0, \end{aligned}$$
(1)

\(\alpha \) stands for the depth of parabolic potential. According to approach reported in [11], the solution of Eq. (1) with a arbitrary initial beam \(\phi (x,0)\) can be written as [11, 14]:

$$\begin{aligned} \phi (x,z)=f(x,z)\int \nolimits _{-\infty }^{+\infty }\left[ \phi (\xi ,0)e^{ib\xi ^{2}}\right] e^{-iK\xi }d\xi , \end{aligned}$$
(2)

where \(b=\alpha \cot (\alpha z)/2\) and \(K=\alpha x\csc (\alpha z)\) are the corresponding spatial frequency and:

$$\begin{aligned} f(x,z)=e^{ibx^{2}}\sqrt{-\frac{i}{2\pi }\frac{K}{x}}. \end{aligned}$$

Then, employing the convolution property of Fourier transform, Eq. (2) can be rewritten as:

$$\begin{aligned} \phi (x,z)=f(x,z)\frac{1}{2\pi }\int \nolimits _{-\infty }^{+\infty }{\widehat{\phi }}(k,0){\widehat{G}}(K-k)dk, \end{aligned}$$
(3)

where, \({\widehat{\phi }}(k,0)\) and \({\widehat{G}}(k)\) are the Fourier transform of \(\phi (x,0)\) and \(e^{ibx^{2}}\), respectively. To obtain the dynamic solution for Eq. (1), we need to calculate the Fourier transforms of the input beam \(\phi (x,0)\) and \(\exp (ibx^{2})\), respectively. Before considering the effect of initial chirp on the dynamics of the optical beam, it is necessary to know the dynamics of the optical beam without chirp. Therefore, the input beam is taken as a Gaussian beam without the chirp:

$$\begin{aligned} \phi (x,0)=\frac{1}{\root 4 \of {\pi }}\exp \left( -\frac{x^{2}}{2}\right) . \end{aligned}$$
(4)

According to (3), we first calculate the Fourier transforms of \(\phi (x,0)\) and \(G(x)=\exp (ibx^{2})\) as:

$$\begin{aligned} {\widehat{\phi }}(k,0)=\sqrt{2}\root 4 \of {\pi }\exp \left( -\frac{1}{2} k^{2}\right) \end{aligned}$$
(5)

and

$$\begin{aligned} {\widehat{G}}(k)=\sqrt{i\frac{\pi }{b}}\exp \left( -\frac{i}{4b}k^{2}\right) . \end{aligned}$$
(6)

Substituting Eqs. (5) and (6) into Eq. (3), we can readily obtain the propagation solution of Eq. (1) corresponding to the initial beam (4):

$$\begin{aligned} \left| \phi (x,z)\right|&=\left| \frac{1}{\root 4 \of {\pi }}\sqrt{ \frac{\alpha }{\alpha \cos \left( \alpha z\right) +i\sin \left( \alpha z\right) }}\right| \nonumber \\&\quad \times \exp \left\{ -\frac{x^{2}}{2\left[ \alpha ^{2}\cos ^{2}\left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) \right] /\alpha ^{2}} \right\} . \end{aligned}$$
(7)
Fig. 1
figure 1

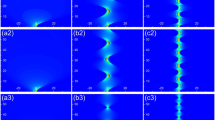
(Color online) The evolution of the Gaussian beam without the chirp governed by Eq. (7) for different \(\alpha \). a \(\alpha =0.5\), b \(\alpha =1\), and c \(\alpha =1.5\) . The evolution of the beam’s d peak and e width governed by Eq. (8) for different \(\alpha \). In Fig. 1d, e, the red, black, and blue curves correspond to the case of \(\alpha =0.5\), 1, and 1.5, respectively

Full size image

According to Eq. (7), we plot the evolutions of the optical beam for the different \(\alpha \), and the results are shown in Fig. 1a–c. Clearly, one can see from Fig. 1a–c that when \(\alpha \ne 1\), the beam exhibits a periodic breathing behavior. While the beam is stable in their entire propagation distance for \(\alpha =1\), which agree with the results reported in [16]. As we all know, when \(\alpha =1\), input state (4) is a stationary solution of Eq. (1) in quantum mechanics. Moreover, from Eq. (7), one can find that the trajectories, the maximum amplitude, and the width of the beam are of the form:

$$\begin{aligned} x&=0, \nonumber \\ I_{m}&=\frac{1}{\sqrt{\pi }}\sqrt{\frac{\alpha ^{2}}{\alpha ^{2}\cos \left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) }}, \nonumber \\ W&=\sqrt{\frac{\alpha ^{2}\cos ^{2}\left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) }{\alpha ^{2}}}. \end{aligned}$$
(8)

From Eq. (8), one can find that the center of the beam is always located at \(x=0\). When \(\alpha \ne 1\), the width and peak of the beam change periodically, so the beam exhibits a periodic breathing behavior, and their evolutions are shown in Fig. 1d, e. While \(\alpha =1\), the width and peak of the beam are \(P=1/\sqrt{\pi }\ \)and \(W=1\), and remain the same (Fig. 1d, e). In the following, we will consider the effect of initial chirp on the dynamics of the optical beam.

3 The influence of the linear chirp on the dynamics of the optical beam

In this section, we will consider the effect of initial linear chirp on the dynamics of the optical beam. Thus, the initial beam is taken as Gaussian beam with a linear chirp:

$$\begin{aligned} \phi (x,0)=\frac{1}{\root 4 \of {\pi }}\exp \left( -\frac{x^{2}}{2}\right) \exp \left( iCx\right) ; \end{aligned}$$
(9)

here, C is a linear chirp parameter. Then, we calculate the Fourier transforms of \(\phi (x,0)\) as:

$$\begin{aligned} {\widehat{\phi }}(k,0)=\sqrt{2}\root 4 \of {\pi }\exp \left[ -\frac{1}{2}\left( k-C\right) ^{2}\right] . \end{aligned}$$
(10)

Substituting Eqs. (10) and (6) into Eq. (3), we get:

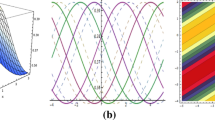
$$\begin{aligned} \left| \phi (x,z)\right|&=\left| \frac{1}{\root 4 \of {\pi }}\sqrt{ \frac{\alpha }{\alpha \cos \left( \alpha z\right) +i\sin \left( \alpha z\right) }}\right| \nonumber \\&\quad \times \exp \left\{ -\frac{\left[ x-\left( C/\alpha \right) \sin \left( \alpha z\right) \right] ^{2}}{2\left[ \alpha ^{2}\cos ^{2}\left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) \right] /\alpha ^{2}}\right\} . \end{aligned}$$
(11)

According to Eq. (11), we plot the evolution of the optical beam for the different \(\alpha \), and the corresponding results are shown in Fig. 2a–c. From them, one can see that under the action of the linear chirp, the beam exhibits a periodically oscillating behavior. Moreover, from Eq. (11), one can find that the trajectories, the maximum amplitude, and the width of the beam are of the form:

$$\begin{aligned} x&=\left( C/\alpha \right) \sin \left( \alpha z\right) , \nonumber \\ I_{m}&=\frac{1}{\sqrt{\pi }}\sqrt{\frac{\alpha ^{2}}{\alpha ^{2}\cos \left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) }}, \nonumber \\ W&=\sqrt{\frac{\alpha ^{2}\cos ^{2}\left( \alpha z\right) +\sin ^{2}\left( \alpha z\right) }{\alpha ^{2}}}. \end{aligned}$$
(12)

From the trajectory equation \(x=\left( C/\alpha \right) \sin \left( \alpha z\right) \), one can easily see that the beam exhibits a sine oscillating behavior induced by the linear chirp, and the oscillating amplitude is proportional to the linear chirp parameter; the results are shown in Fig. 2d. From the last two equations of Eq. (12), we can see that the evolution of the beam’s peak and width are independent of the linear chirp parameter, so their evolutions are the same as that of the beam without the chirp (see Fig. 1d, e). Thus, we conclude that the linear chirp of beam can induce a periodically oscillating behavior of beam, but it does not affect on the evolution of the beam’s peak and width. In the other words, the evolution of the beam’s peak and width depend only on the depth of parabolic potential \(\alpha \).

Fig. 2
figure 2

(Color online) The evolution of the Gaussian beam with the linear chirp governed by Eq. (11) when \(C=2\). a \(\alpha =0.5\), b \(\alpha =1\), and c \(\alpha =1.5\). d The oscillating amplitude versus the parameter C for different \(\alpha \)

Full size image

4 The effect of the quadratic chirp on the dynamics of the optical beam

In this section, we will consider the influences of initial quadratic chirp on the dynamics of the optical beam. Thus, the initial beam is taken as Gaussian beam with a quadratic chirp:

$$\begin{aligned} \phi (x,0)=\frac{1}{\root 4 \of {\pi }}\exp \left( -\frac{x^{2}}{2}\right) \exp \left( i\beta x^{2}\right) , \end{aligned}$$
(13)

with \(\beta \) being the quadratic chirp parameter, and its Fourier transforms can be written as:

$$\begin{aligned} {\widehat{\phi }}(k,0)=\frac{1}{\root 4 \of {\pi }}\sqrt{\frac{\pi }{\left( 1/2-i\beta \right) }}\exp \left( -\frac{k^{2}}{2-i4\beta }\right) . \end{aligned}$$
(14)

Substituting Eqs. (14) and (6) into Eq. (3), the propagation solution of Eq. (1) corresponding to this initial beam (13) can be written as:

$$\begin{aligned} \left| \phi (x,z)\right|&=\left| \frac{1}{\root 4 \of {\pi }}\sqrt{ \frac{\alpha }{\alpha \cos \left( \alpha z\right) +i\sin \left( \alpha z\right) +2\beta \sin \left( \alpha z\right) }}\right| \nonumber \\&\exp \left\{ -\frac{x^{2}}{2\frac{\left\{ \alpha ^{2}\left[ \frac{2\beta }{ \alpha }\sin \left( \alpha z\right) +\cos \left( \alpha z\right) \right] ^{2}+\sin ^{2}\left( \alpha z\right) \right\} }{\alpha ^{2}}}\right\} . \end{aligned}$$
(15)
Fig. 3
figure 3

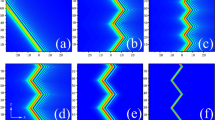
(Color online) The evolution of the Gaussian beam with the quadratic chirp governed by Eq. (11) when \(\beta =1\). a \(\alpha =0.5\), b \(\alpha =1\), and c \(\alpha =1.5\). The evolution of the beam’s width governed by Eq. (8) for different \(\alpha \); d \(\alpha =0.5\), e \(\alpha =1\), and f \(\alpha =1.5\)

Full size image

According to Eq. (15), we plot the evolution of the optical beam for the different \(\alpha \), and the corresponding results are shown in Fig. 3a–c. From them, one can see that under action of the quadratic chirp, the beam exhibits a periodically breathing behavior. Moreover, from Eq. (15), one can find that the trajectories, the maximum amplitude and the width of the beam are of the form:

$$\begin{aligned} x&=0, \nonumber \\ I_{m}&=\frac{1}{\sqrt{\pi }}\left| \sqrt{\frac{\alpha }{\alpha \cos \left( \alpha z\right) +i\sin \left( \alpha z\right) +2\beta \sin \left( \alpha z\right) }}\right| ^{2}, \nonumber \\ W&=\sqrt{\frac{\alpha ^{2}\left[ \frac{2\beta }{\alpha }\sin \left( \alpha z\right) +\cos \left( \alpha z\right) \right] ^{2}+\sin ^{2}\left( \alpha z\right) }{\alpha ^{2}}}. \end{aligned}$$
(16)

From Eq. (16), one can find that the center of the beam is \(x=0\), while the peak and the width of the beam vary periodically, even if when \( \alpha =1\). Thus, it can be concluded that the quadratic chirp parameter can induce a periodically breathing behavior and does not affect the center of the beam. The above results are consistent with what reported in [26]; however, the analytical method in our paper is more direct and effective. In addition, we note that the maximum amplitude \(I_{m}\) and the width W satisfy the following relationships \(I_{m}=1/\left( W\sqrt{\pi }\right) \), so we only consider the evolution of width governed by Eq. (16), as shown in Fig. 3d–f. From Fig. 3d–f, one can see that due to the action of the quadratic chirp parameter, the dynamics of the optical beam differs from that without chirp. Specifically, the quadratic chirp parameter can affect the maximum width and its corresponding location where the maximum width occurs.

5 Conclusions

In summary, based on the linear Schrödinger equation with the parabolic potential, using the approach reported in [11], we have analytically investigated the effect of initial chirp on the dynamics of the optical beam. For linear chirp, the results have shown that the linear chirp of beam can induce a periodically oscillating behavior, but it does not affect on the evolution of the beam’s peak and width. The oscillating amplitude is proportional to the linear chirp parameter. For the quadratic chirp, the results have shown that the quadratic chirp of beam can induce a periodically breathing behavior and affect the evolution of beam’s peak and width.