An ultrastable laser system at 689 nm for cooling and trapping of strontium

Abstract

We present a 689-nm cavity-based laser system for cooling and trapping strontium atoms. The laser is stabilized to a high-finesse cavity by the Pound–Drever–Hall technique, exhibiting a frequency stability in the $10^{-14}$ range for averaging times up to 100 s. A cavity drift of 8 kHz per day is mapped out and compensated. At short times, the laser exhibits a linewidth of a few kilohertz. With this laser system, we realize a magneto-optical trap of strontium operated on the narrow inter-combination transition yielding sub-microkelvin temperatures, and demonstrate absorption spectroscopy on the strontium inter-combination line.

1 Introduction

Laser cooling and trapping using the narrow-line transitions in alkaline-earth-like atoms has enabled efficient production of quantum degenerate gases of those species, opening up new perspectives in many research frontiers, e.g., precision measurement [1], Rydberg physics [2], and dipolar physics with highly magnetic atoms [3,4,5]. The realization of an efficient narrow-line cooling requires a laser with a short-term laser frequency stability better than the transition natural linewidth $\Gamma$. For example, the inter-combination line $5s^2~^1\mathrm{S}_0~\rightarrow ~5s5p~^3\mathrm{P}_1$ of strontium has $\Gamma = 7.5$ kHz resulting in a Doppler temperature of $\sim$ 180 nK, which is even lower than the single-photon recoil temperature of 460 nK.

Locking to an ultrastable cavity using the Pound–Drever–Hall (PDH) technique is a widely used and powerful approach to stabilize the laser frequency and to reduce the laser linewidth [6, 7]. Here, we provide a simple yet complete recipe for constructing and characterizing a 689-nm cavity-based laser system, which is used for cooling and trapping strontium atoms in a narrow-line magneto-optical trap (MOT). We realize a $91\%$ mode-matching efficiency to a high-finesse ultrastable cavity ($F \sim 200{,}000$), which enables a tight stabilization of our ${689}\,\hbox { nm}$ laser to the cavity. The short-term linewidth of the locked laser is estimated to be about ${3}\hbox { kHz}$ and a stability of $10^{-14}$ is shown for timescales of minutes using the cavity itself as a stable reference. A long-term drift of 8 kHz/day is measured and compensated by Doppler-free spectroscopy on the strontium inter-combination transition. The locked laser is applied in our experiment to cool and trap strontium atoms on the inter-combination transition and a sub-$\upmu \hbox {K}$ MOT is achieved. We also demonstrate a narrow-line absorption measurement on the ultracold cloud with this laser. The main goal of this article is to describe the technical details for setting up a cavity-based strontium narrow-line cooling laser system motivated by the rapidly increasing interest in ultracold strontium gases [8].

Detailed information on trapping strontium via the inter-combination line can already be found in many previous publications (see, e.g., [9,10,11,12,13,14,15]). However, to our best knowledge, a compact collection of those widely spread information does not exist yet. Furthermore, our laser system comprises some unique features like, e.g., the cavity with high finesse, and offers a large degree of conceptual simplicity. The article is organized as follows: in Sect. 2, we describe in detail how the cavity-based ${689}\hbox { nm}$ laser system is realized and characterized. Then application of the laser system to cooling, trapping, and detecting strontium atoms is demonstrated in Sect. 3.

2 Narrow-line laser system at 689 nm

2.1 Overview

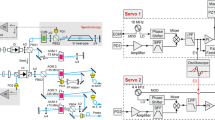
The 689-nm laser is a commercial extended-cavity diode laser (ECDL) amplified by a tapered amplifier (TA Pro, Toptica), delivering a power of $\sim 90\,\hbox { mW}$. As depicted in Fig. 1, the output of this laser is split into four optical channels, two for the frequency stabilization and the other two for the main experiment.

Fig. 1

Schematic of the 689-nm laser system. The three different components together with the commercial laser are depicted: Pound–Drever–Hall (PDH) frequency stabilization, long-term drift compensation, and the setup for running the magneto-optical trap (MOT). HWP half wave-plate, QWP quarter wave-plate, PBS polarizing beam splitter, AOM acousto-optic modulator, BS beam splitter, BD beam dump, EOM electro-optic modulator, PD photodiode, ISO optical isolator, ULE cavity ultralow expansion cavity. Details can be found in the main text

The PDH stabilization component is drawn at the bottom right in Fig. 1, where a beam of $\sim 200\, \upmu \,\hbox {W}$ is guided into a high-finesse cavity after passing a resonant-type electro-optic modulator (EOM) and a double-pass acousto-optic modulator (AOM). The commercial ultrastable FP cavity (ATF 6020-4 Notched Cavity, Stable Laser Systems) is chosen to act as a frequency reference. The two cavity mirrors (one flat and the other one concave) are optically contacted to a 10-cm-long Zerodur spacer ($L\approx \,10\hbox { cm}$). The cavity is placed in a high-vacuum housing (${1\times 10^{-7}}\hbox { Torr}$), the inner temperature of which is actively stabilized to the cavity zero-crossing temperature of $27.8\,^ \circ {\mathrm{C}}$ [16]. The whole system is supported by a vibration-free platform. The EOM is driven by a DDS-based radio-frequency (RF) generator (AD9914, Analog Devices) to modulate the phase of the cavity incident laser field at a frequency of ${240.96}\hbox { MHz}$. The $\hbox {AOM}_2$ in Fig. 1 is driven by another RF generator of the same type at $\sim 80\hbox { MHz}$ for tuning the relative frequency between the cavity mode and the laser. All the RF generators in our experiment are referenced to a commercial rubidium frequency standard (FS725, SRS). A high-bandwidth ultralow-noise photodiode ($\hbox {PD}_-\hbox {r}$) is used to detect the reflected field strength, which gives the PDH error signal after demodulation.

As seen at the bottom left of Fig. 1, a Doppler-free saturation spectroscopy on the strontium inter-combination line is set up for the compensation of the long-term cavity drift. A strong pump beam and a weak counter-propagating probe beam are overlapped in a commercial strontium heatpipe (from LEOSolutions). The pump beam is frequency modulated by a double-pass AOM and the transmission of probe beam through the heatpipe is demodulated to give an error signal. The details about the saturation spectroscopy are given in Sect. 2.3.1.

The remaining laser output is used distributing the light to the main experiment. About $80\%$ of the total laser power is sent to the strontium MOT setup, as shown at the top left of Fig. 1. Another part of the laser light is used to stabilize a transfer cavity, to which a narrow-line 318-nm UV laser for Rydberg excitation of strontium is locked. The 689-nm laser together with the 318-nm laser drive a two-photon excitation from the strontium ground state to triplet Rydberg states [17].

2.2 Laser frequency stabilization

2.2.1 Cavity ring-down spectroscopy

To obtain free spectral range (FSR) of the ULE cavity, we linearly scan the laser frequency over two adjacent cavity fundamental modes with the EOM. The calibration of the frequency axis is done by the frequency difference between two first-order modulation sidebands ($2\times 240.96 \hbox { MHz}$). The FSR is determined as 1.454(1)GHz.

Fig. 2

Cavity ring-down spectroscopy of the high-finesse ULE cavity. Upper panel: the time evolution of the cavity transmission after the incident laser beam is turned off. The experimental data at $t>0$ (black dots) is fitted to an exponential decay (red curve) with a decay constant of $21.378(5)\, \upmu \hbox {s}$. Lower panel: the time evolution of the cavity transmission when the laser frequency is scanned at a rate of 12.5 $\hbox {kHz/}\upmu \hbox {s}$. Both the experimental data (black dots) and a theoretical simulation according to Eq. 1 without any free parameters (red curve, see text) are shown. The inset shows the first derivatives of both to reveal the effect of laser phase fluctuations. A $\pi$ phase difference between measurement and simulation is accumulated in the time interval ${27 \,\upmu \hbox {s}}$ $\lesssim t\lesssim$ ${35\, \upmu \hbox {s}}$, as indicated by the blue dashed lines

A cavity ring-down measurement [18] is performed to characterize the cavity finesse. As shown at the top of Fig.  2, the cavity transmission undergoes an exponential decay after the incident laser field is instantaneously turned off. The 1 / e decay time is fitted to be $\tau =21.378(5)~\upmu \hbox {s}$, which gives a cavity linewidth with a full width at half maximum (FWHM) of $v_{\mathrm{{FWHM}}}=1/(2\pi \tau )=$ ${7.445(2)}\,\hbox {kHz}$ [19]. The cavity finesse is then given by $F=2\pi \tau v_{\mathrm{{FSR}}}=195.3(1)\times 10^3$.

The high finesse of the cavity allows us to use a variant of the ring-down technique for the characterization of the short-term laser noise [20], in which the laser is linearly scanned instead of being shut off. As seen at the bottom of Fig.  2b, we observe an oscillatory decay of the transmission, which can be described by [20]

$$\begin{aligned} I_\mathrm{T}(t)=\frac{2I_i\exp \left[ -\frac{1}{2}\left( \frac{\tau _0}{\tau }+\frac{2\omega _0}{\tau {\dot{\omega }}}\right) \right] }{{\dot{\omega }}\left( \sqrt{\tau _0^2+16\tau ^2}-\tau _0\right) }\exp (-t/\tau )|\text {erfc}[\Lambda (t)]|^2, \end{aligned}$$

(1)

where $I_i$ is the incident intensity, $\omega ={\dot{\omega }}t+\omega _0$ is the laser angular frequency with ${\dot{\omega }}=2\pi \times {12.5}{\hbox { kHz}/\upmu \hbox {s}}$, $\tau _0=1/v_{\text {FSR}}$ is the time taken for the light to make one round trip in the cavity, and erfc is the error function with the argument

$$\begin{aligned} \Lambda (t)=-\frac{1+i}{2}\sqrt{{\dot{\omega }}}t+\frac{1-2\tau \omega _0 +\tau \tau _0{\dot{\omega }}-i(1+2\tau \omega _0 -\tau \tau _0{\dot{\omega }})}{4\tau \sqrt{{\dot{\omega }}}}. \end{aligned}$$

We find a good agreement between the measurement and Eq. 1 without any free parameters for $t\lesssim {30}\,{\upmu \hbox {s}}$, as seen in the lower panel of Fig.  2b. The deviation for $t\gtrsim$ ${30}\,{\upmu \hbox {s}}$ can be attributed to phase fluctuations of the free-running laser [20] resulting in a $\pi$ phase difference between measurement and simulation within $\Delta t\sim ~{8}\,{\upmu \hbox {s}}$. The short-term laser frequency noise can be estimated as $\pi /(2\pi \Delta t^2)\sim {150}\,{\hbox {kHz}/20\,\upmu \hbox {s}}$. This frequency instability is actually much larger than the ${7.5}\hbox { kHz}$ natural linewidth of the inter-combination transition on a timescale of the excited state (5s5p $^3\text {P}_1$) lifetime $({21}\,{\upmu \hbox {s}})$, thus requiring careful stabilization of the laser frequency as described in Sect. 2.2.3.

2.2.2 Mode matching

Tight PDH locking requires careful mode matching between the spatial modes of the incident laser field and the cavity. The spatial modes are spectrally resolved, allowing one to measure the transmission $T_{nm}$ of each transverse Hermite–Gaussian mode $\hbox {TEM}_{nm}$ separately and to deduce the mode-matching efficiency of the fundamental mode by $\eta =T_{00}/\sum \nolimits _{n',m'}T_{n'm'}$. Here, n and m are mode orders, and modes with the same $n+m$ value are degenerate. Since the free-running laser linewidth is much larger than that of the cavity, fluctuations of the transmission are observed when the laser frequency is scanned over the cavity resonance. To overcome this effect, we repeat the scan around each transverse mode 100 times. The resulting histograms are plotted in Fig. 3. Three resonances, corresponding to $n+m=0,1,2$, are beyond the detection limit. We fit Gaussian distributions to the histograms to extract the centers ${\bar{T}}_{nm}$ and the widths $\sigma _{nm}$. In this way, the mode-matching efficiency of the fundamental mode is found out to be $\eta =0.91(3)$.

Fig. 3

Histogram of the cavity transmission when the laser frequency is repeatedly scanned ($\sim {0.04}\,\hbox {kHz}/\mu \hbox {s}$) over the three cavity resonances corresponding to different spatial modes, i.e., TEM$_{00}$, TEM$_{10,01}$, and TEM$_{20,02,11}$. The black curves are fitted Gaussian distributions to extract out the centers ${\bar{T}}_{nm}$ and widths $\sigma _{nm}$ yielding transmissions of 1.0(3) (TEM$_{00}$), 0.09(2) (TEM$_{10,01}$) and 0.009(2) (TEM$_{20,02,11}$). The detection limit is indicated by the gray-shaded area

2.2.3 Pound–Drever–Hall stabilization

Following the standard PDH locking method [7], an error signal is obtained by demodulating the cavity reflection with the EOM phase modulation frequency using a RF mixer, as shown at the bottom of Fig. 4. We have calibrated the error-signal slope as $D\sim {0.03} \hbox { V/kHz}$ at the cavity resonance. A commercial servo (FALC-110, Toptica) is used to provide feedback to the laser diode current (the control voltage of the ECDL piezo) for a fast (slow) error correction. The unity-gain bandwidth of the servo is about ${1.7}\hbox { MHz}$, measured by the in-loop error signal noise with a RF spectrum analyzer (N9343C, KEYSIGHT). After the laser is locked, the root-mean-square (RMS) error signal $V_{\text {rms}}$ is about ${0.043}\hbox { V}$ shown at the top of Fig. 4. Assuming Gaussian noise on the laser, we can obtain an estimate of the closed-loop laser linewidth of $2.355V_{\text {rms}}/D\approx$ ${3.4}\hbox { kHz}$ [7].

Fig. 4

Transmission signal of the ULE cavity (upper graph) and the corresponding PDH error signal (lower graph) for a closed servo loop. On the right axis, the voltage of the error signal has been converted into a frequency scale

We can recheck the mode-matching efficiency measurement in Sect. 2.2.2 by carefully monitoring the normalized cavity transmission $p_\mathrm{t}$ and reflection $p_\mathrm{r}$ when the laser is locked. From Equation 2 in Ref. [21] we can derive the expression $\eta =(1+p_\mathrm{t}-p_\mathrm{r})^2/4p_\mathrm{t}$. In Fig. 4, we show $p_{\mathrm{t}}$ when the laser is locked to the cavity with $p_\mathrm{t}\approx 0.29$. Under the closed servo loop condition, $p_\mathrm{r}$ is about 0.27, which gives mode matching to the $\hbox {TEM}_{00}$ mode of $\eta \approx 0.90$, in very good agreement with the mode-matching measurement in the previous section. We can also obtain information about the cavity mirror transmission T and loss l following Ref. [21]. The results are $T=$ ${9.1}\hbox { ppm}$ and $l=$ ${7.2}\hbox { ppm}$ matching with the specifications of the manufacturer.

2.3 Characterization of laser frequency stability

2.3.1 Frequency drift of ULE cavity

It is well known that even an ULE cavity suffers from a very small and slow drift in its effective length, and thus a long-term frequency excursion on the order of ${10}\hbox { kHz}$ per day for the locked laser [22]. To measure and compensate this small, yet non-negligible drift, we set up a Doppler-free absorption spectroscopy on the ${689}\hbox { nm}$ strontium narrow-line inter-combination transition to serve as an absolute frequency reference. As shown in Fig. 1, a probe and a counter-propagating pump are sent through a Sr heatpipe, which is heated to about ${470}^{\,\circ }\hbox {C}$ to increase the optical density (OD). The $1/e^2$ diameter of the two beams is about 5 mm and the pump (probe) beam power is ${\sim 800 (200)}{\mu \hbox {W}}$. In Fig.  5a, we show the resulting probe transmission lineshape, where the on-resonance absorption is about $10\%$ and the Lamp dip amplitude is about $1.5\%$. The FWHM of the lamb dip is ${2.5(5)}\hbox { MHz}$, which is mainly caused by particle collisions [23] with a small contribution from power broadening.

Fig. 5

Doppler-free spectroscopy of the $^{88}$Sr inter-combination transition. a Transmission spectrum with Lamb dip. The Doppler-broadened absorption spectrum has a FWHM of ${0.908(2)}\hbox { GHz}$ from a Gaussian fit (red solid curve), which corresponds to an atomic temperature of 474(3) $^{\circ }\hbox {C}$. The inset shows the Lamb dip of the center of the absorption spectrum. A Lorentz fit (blue solid curve) yields a FWHM of ${2.5(5)}\hbox { MHz}$. b Error signal generated by modulation transfer of the Doppler-free absorption spectroscopy. The signal is fitted to a double-Gaussian function (red curve) to confirm that the signal is symmetric and to obtain the slope on resonance (see text)

Fig. 6

The long-term laser frequency stability. a The cavity long-term drift. The measured cavity resonance (open dots) is fitted to a line with a slope of ${8(1)}{\hbox { kHz/day}}$, where the uncertainty comes from the systematic frequency determination (see text). b Allan deviation measured with respect to the ultrastable cavity. The solid line is a guide for the eye

A double-pass AOM ($\hbox {AOM}_{1}$ in Fig. 1) is inserted into the pump beam to generate a ${40}\hbox { kHz}$ frequency modulation, which gives rise to a modulation transfer to the probe beam transmission [24]. The signal from $\hbox {PD}_{-}\hbox {s}$ in Fig. 1 is demodulated by a lock-in amplifier with an integration time of ${100}\hbox { ms}$. In our setup, the 40-kHz modulation frequency is small with respect to the observed FWHM of the Lamb dip and we use a large modulation index ($>20$), which provides an optimal slope of the demodulated signal on atomic resonance [25]. To minimize the so-called residual amplitude modulation (RAM), we carefully align the double-pass AOM as well as the spatial overlap between the pump and probe beams, resulting in a symmetric demodulated signal shown in Fig.  5b. The red curve is a fit to a double-Gaussian function, which gives a height (width) difference of about $2\%$ ($0.3\%$) for the two peaks. The resulting slope at zero detuning is about ${1.2}\hbox { V/MHz}$.

To determine the resonance frequency on a day-to-day basis, we stabilize the laser frequency following the scheme as described in Sect. 2.2.3 and adjust the modulation frequency of $\hbox {AOM}_2$ in Fig. 1 to zero the error signal shown in Fig. 5. The modulation frequency then serves as a relative measure for the actual cavity frequency. In Fig.  6a, daily measurements of the relative ULE frequency are shown for a time window spanning more than three months. We observe a linear frequency drift of ${8(1)}\hbox { kHz}$ per day. We attribute this long-term drift to the excursion of the cavity length, as other systematic effects may not create such a monotonic drift over months. On the other hand, systematics like RAM, magnetic field fluctuations, misalignment between probe and pump beams, can cause perturbations on a shorter timescale. In Sect. 3.2, we will show a month-long stability of a narrow-line absorption imaging of cold strontium atoms using the locked and drift-compensated laser.

2.3.2 Allan deviation

Since our ultrastable cavity exhibits a daily drift of only ${8}\hbox { kHz}$, we can use it as a sufficient secondary reference in order to determine frequency excursions of the laser on timescales of minutes or hours. To determine the frequency stability of our laser system in this regime, we lock the laser at the half maximum of the cavity transmission by adding a constant offset to the PDH error signal, such that the laser frequency fluctuation $\delta v$ with respect to the cavity resonance is translated into a fluctuation of transmission amplitude $\delta U_\mathrm{T}$ through a linear relation $\delta v=k\cdot \delta V_\mathrm{T}$ ($k=v_{\text {FWHM}}/V_{\mathrm{pp}}$ with the peak-to-peak transmission amplitude $V_{\mathrm{pp}}$ as discussed in Sect. 2.2.3). The cavity acts as a low-pass filter with a bandwidth of ${\sim 7.5}\hbox { kHz}$ . We have performed a 3-h measurement of the transmission with a time step of ${1}\hbox { ms}$, during which the cavity drift can be neglected. To minimize the influence of the laser power noise, we actively stabilize the input power for the cavity by using the $\hbox {AOM}_2$ and $\hbox {PD}_-\hbox {p}$ in Fig. 1 with a feedback bandwidth of ${10}{\hbox { kHz}}$.

We compute the non-overlapping Allan deviation [26]

$$\begin{aligned} \sigma _{y}(\tau )=\sqrt{\left\langle \frac{{\bar{y}}_{k+1}-{\bar{y}}_{k}}{2}\right\rangle _{k}}, \end{aligned}$$

(2)

where $y=\delta v/v_0$ is the fractional frequency and ${\bar{y}}_k$ denotes its mean over an averaging time $\tau$: ${\bar{y}}_k=\int _{k\tau }^{(k+1)\tau }y(t)\mathrm{d}t$. As shown in Fig. 6b, we achieve a stability of order $10^{-14}$ for an averaging time up to ${100}\hbox { s}$.

Considering that the laser is tightly locked to the ultrastable cavity, one would naively expect that the above measured Allan deviation should be strictly zero. However, the based-line fluctuation of the error signal coming from, e.g., electronics can cause the observed variations of the Allan deviation shown in Fig.  6b. Linear fitting of Log($\tau _y$) to Log($\tau$) at $\tau<$ ${7}\hbox { ms}$ ($\tau>$ ${6}\hbox { s}$) gives a slope very close to $-1/2$ ($+1/2$) indicating the white noise (random-walk noise) [26]. These fluctuations represent absolute frequency uncertainties of the laser system, although they may be actually caused by the feedback loop.

3 Application to producing and probing ultracold strontium atoms

3.1 Narrow-line magneto-optical trap for strontium

Cooling strontium in a MOT to ultralow temperatures consists of two stages. We start with a three-dimensional broad-line ($\sim 2\pi \times \, {32}\hbox { MHz}$) MOT (bMOT) loaded from a two-dimensional MOT [27] at ${461}\hbox { nm}$ driving the transition $5s^2~^1\mathrm{S}_0~\rightarrow ~5s5p~^1\mathrm{P}_1$, which brings the atomic temperature to several millikelvins. A small leakage from the broad-line transition populates the metastable state $5s5p~^3\mathrm{P}_2$, the sub-states $m_\mathrm{J}=1$ and 2 of which are magnetically trappable [28]. The atoms entering the second-stage cooling are from the pure magnetic trap, where a short repumping pulse operating on the transition $5s5p~^3\mathrm{P}_2~\rightarrow ~5p^2~^3\mathrm{P}_2$ [29] burst the atoms into the narrow-line cooling transition $5s^2~^1\mathrm{S}_0~\rightarrow ~5s5p~^3\mathrm{P}_1$.

Fig. 7

Temperature T (open circles) and atom number (open squares) for a narrow-line strontium MOT versus the single-beam cooling saturation parameter s at a detuning of ${-500}\hbox { kHz}$. The error bars represent the fitting errors when measuring T and the standard deviations for five measurements of atom number at each s. The black dashed curve depicts a fit of T at large s to $N_R(\sqrt{1+s}\hbar \Gamma /2k_b)$ yielding the numerical factor $N_R = 2.26(2)$ (see text)

The narrow-line MOT (nMOT) beams are overlapped with the bMOT ones and have $1/e^2$ waists of about ${4.4}\hbox { mm}$. The magnetic field gradient is about ${5}\hbox { G/cm}$ during the nMOT and the transfer efficiency from the bMOT to nMOt is about $30\%$. Due to the mK temperature of atoms in the magnetic trap, the frequency of the ${689}\hbox { nm}$ laser is first broadened to match the Doppler linewidth, referred to as the broadband phase, and then changed to a single line [8]. The whole nMOT cooling phase lasts for about ${200}\hbox { ms}$, after which a gas of $\sim 1\times 10^6$ atoms around ${1}\,{\upmu \hbox {K}}$ can be produced. The atomic density in our nMOT is about ${1\times 10^{11}}{\hbox {cm}^{-3}}$, well below the density regime where the so-called radiation trapping limits the nMOT temperature [30].

As shown in Fig. 7, the nMOT temperature and atom number are plotted versus the single-beam saturation parameter s at a detuning of ${-500}\,{\hbox {kHz}}$. Here the atom number is determined by standard absorption imaging on the broad-line transition and the temperature is measured via the ballistic time-of-flight technique [31]. Due to a large oscillatory motion of atoms in the nMOT in the horizontal direction [30], the vertical temperature is presented in Fig. 7. At large s the semiclassical theory predicts $T(s)=N_\mathrm{R}(\sqrt{1+s}\,\hbar \Gamma /2k_\mathrm{b})$ [32, 33], which is observed in Fig. 7 with the fitted numerical factor $N_\mathrm{R}=2.26(2)$. Here $\hbar$ and $k_\mathrm{b}$ are the reduced Planck and the Boltzmann constant, respectively. Due to an imperfect transition from the broadband phase to the single-line one in the nMOT, we observe a significant atom number decrease when s is reduced.

In the low-saturation regime ($s\sim 1$), a laser linewidth better than the ${7.5} \hbox { kHz}$ natural linewidth is decisive for achieving atomic temperatures in the sub-$\upmu$K range [13, 34]. We have realized a 500-nK nMOT with an atom number of $\sim 2\times 10^5$ at $s\approx 3$, which confirms that the frequency stability of our laser system on the relevant timescale of the trapping is indeed at a level of ${10}\hbox { kHz}$ or below.

3.2 Absorption imaging on the inter-combination line

As an additional application of our narrow-band laser system, we perform absorption imaging of the ultracold strontium gas on the inter-combination transition [35]. The horizontally propagating imaging beam has a $1/e^2$ waist of ${2.63}\hbox { mm}$ ($\gg$ the atomic size $\le {200}{\mu \hbox {m}}$) and we use a power of $\sim$ ${5.5}{\mu \hbox {W}}$ (the peak saturation parameter $s\approx 17$) with a pulse length of ${200}\,{\mu \hbox {s}}$, which is much longer than the excited state lifetime of about ${21}\,{\mu \hbox {s}}$.

Fig. 8

Absorption spectrum on the magnetically insensitive transition $^1\mathrm{S}_0$ ($m_J=0$) $\rightarrow$ $^3\mathrm{P}_1$ ($m_{J'}=0$) of $^{88}\hbox {Sr}$. The probe frequency is sampled in steps of ${5}\hbox { kHz}$ and the measurement is repeated twice. The red solid curve is a fit to Voigt function (see text for details). Inset: residual linewidth at different atomic temperatures after deconvolution of the absorption spectrum. The calculated Doppler width for a given temperature is indicated by the black dashed curve. The orange dashed line depicts the expected power-broadened Lorentz width of ${32}\hbox { kHz}$ as deduced from the laser intensity

Figure 8 shows an absorption spectrum for the $^1\mathrm{S}_0$ ($m_J=0$) $\rightarrow ^3\mathrm{P}_1$ ($m_{J'}=0$) transition at a cloud temperature of ${1.1}\,{\upmu \hbox {K}}$. The Doppler-broadened Gaussian FWHM is $\sqrt{8\ln 2k_\mathrm{b}T/m\lambda ^2}= {35}\,{\hbox {kHz}}$ and the power-broadened Lorentzian FWHM is $\sqrt{1+s}\Gamma \sim$ ${32}\hbox { kHz}$. Here, m is the $^{88}\hbox {Sr}$ atomic mass and $\lambda$ is the wavelength of the inter-combination transition. Due to similar contributions from both effects, a Voigt function with a Gaussian width determined by the temperature is used to fit the observed lineshape (solid red curve in Fig. 8). This yields a Lorentzian width of ${33(2)}\hbox { kHz}$, which agrees well with the expected linewidth including the effect of power broadening.

To further justify fitting to the Voigt function, we measure the absorption lineshape at different temperatures and perform the same fitting procedure. The resulting Lorentzian width is plotted against T in the inset of Fig. 8 together with the Doppler- (black curve) and power-broadened (orange curve) width. Obviously, the residual Lorentzian (homogeneous) component of the line width does not depend on temperature, justifying our assumption that the lineshape is solely determined by the combined effect of temperature and a homogenous broadening. The fact that the measured residual width of ${32}\hbox { kHz}$ matches the expected power broadening confirms our earlier conclusion that the effective laser linewidth is in the few kHz range or lower.

The absorption spectrum can also be used as a measure for the long-term frequency stability by recording of the resonance frequency on a daily basis. In fact, the measured resonance frequency in the absorption spectrum fluctuates within ${50}\hbox { kHz}$ over a few months while the compensated drift is about ${500}\hbox { kHz}$, which nicely confirms our approach for compensating of the long-term cavity drift as outlined in Sect. 2.3.1.

4 Conclusion

In conclusion, we have presented a narrow-line, frequency-stable ${689}\hbox { nm}$ laser system for laser cooling and trapping of strontium atoms. Employing PDH frequency stabilization with a high-finesse ULE cavity results in a linewidth below 10 kHz enabling the efficient creation of an ultracold strontium gas at sub-microkelvin temperatures. Long-term drifts of the ULE cavity over periods of days and weeks are compensated by frequency referencing to Doppler-free spectroscopy in a Sr heatpipe. The laser system can also be used to perform high-resolution absorption spectroscopy on the Sr inter-combination line, thus exploring many-body effects in the light scattering of a dense gas [36]. The favorable short- or long-term frequency stability of this laser can be transferred to other lasers via transfer cavities as, e.g., used in our lab for stabilizing a ${318}\hbox { nm}$ UV laser for Sr Rydberg excitation [37] and a ${481}\hbox { nm}$ diode laser for MOT repumping [29].