1 Introduction

The spontaneous emission of an atom is usually attributed to the fluctuations of the electromagnetic field vacuum state. The existence of vacuum state is a result of electromagnetic field quantization, and thus, in general, for determining the spontaneous emission rate of an atom, the explicit form of the electric field operator is needed. Since the explicit form of vacuum state field operators depends on the kind and geometry of the boundary surfaces, the spontaneous emission rate at the presence of boundary surfaces differs from its free space’s value. For non-dissipative boundaries, using mode functions which satisfy the boundary conditions, electromagnetic fields are usually quantized [1,2,3,4,5,6]. In the presence of dissipative dielectrics, the quantization of electromagnetic field is more complicated to be derived, because in this case, there is a loss in the medium which creates some kind of coupling between the field and a fluctuating reservoir, and therefore the system made of the electromagnetic field and medium is not a closed system. In this case, we can extend the concept of the system and assume that it is constructed from the radiation field, the medium polarization field and the reservoir parts. Now, a microscopic method (instead of a macroscopic one) can be used where by introducing a suitable Lagrangian or Hamiltonian, the electromagnetic field is quantized canonically [7,8,9,10,11,12,13,14]. But in this formalism, the macroscopic properties of the medium, specially the medium dielectric function, are not arbitrary and depends on the form of the introduced coupling between radiation field, polarization field and reservoir oscillators. On the other hand, in a macroscopic approach of the electromagnetic field quantization, the dielectric function is an arbitrary complex function of frequency and, therefore, a general expression for the field operators is introduced (which can be used at the presence of any medium). The Green function approach of electromagnetic field quantization is a macroscopic approach, where using the vector potential Green function tensor and introducing the noise current density operator(with the assumed commutation relations), the electromagnetic field can be quantized in the vicinity of dispersive and dissipative dielectric media [15,16,17,18,19,20,21,22,23,24]. Since, generally in the vicinity of an arbitrary dielectric surface, the surface can approximately be considered flat and also for simplicity, in this paper, in the presence of a dielectric slab, using the Green function approach of electromagnetic field quantization, the vacuum field operators are evaluated and then the spontaneous emission rate of an excited atom in the space near the slab is computed.

In Sect. 2, we review the base formalism of the Green function scheme of the electromagnetic field quantization. In Sect. 3, the vector potential Green function tensor is calculated. In Sect. 4, the field operators are introduced for singlet and doublet polarization parts of vector potential. The commutation relations between the annihilation and the creation operators are derived in Sect. 5. In Sect. 6, using Fermi’s golden rule, the spontaneous emission rate of the atom with electric dipole moment perpendicular and parallel to the slab is derived. In Sect. 7, the spontaneous emission rate in free space and near a perfect conducting plate is investigated and then by choosing a Lorentz model for the dielectric function, the typical variations of the spontaneous emission rate of the atom near the slab are shown. Finally, we summarize and discuss the main results in Sect. 8.

2 The basis of field quantization

The elements of the Green function approach of electromagnetic field quantization have been discussed in [18,19,20,21,22,23,24], and, therefore, here, the basis equations and notations are only summarized. In this formalism, the medium has a complex relative dielectric function of frequency which satisfies Kramers–Kronig relations.

$$\varepsilon \left( {\varvec{r},\omega } \right) = \varepsilon_{r} \left( {\varvec{r},\omega } \right) + i\varepsilon_{i} \left( {\varvec{r},\omega } \right),$$
(1)

where \(\varepsilon_{r} \left( {\varvec{r},\omega } \right)\) and \(\varepsilon_{i} \left( {\varvec{r},\omega } \right)\) are real and imaginary parts of the dielectric function. The field operators are usually written in terms of the positive and negative frequency parts as

$$\hat{\varvec{O}}\left( {\varvec{r},t} \right) = \frac{1}{{\sqrt {2\varvec{\pi}} }}\mathop \int \limits_{0}^{\infty } d\omega \hat{\varvec{O}}^{ + } \left( {\varvec{r},\omega } \right)e^{ - i\omega t} + H.C,$$
(2)

where the positive and negative frequency parts involve only the annihilation and creation operators, respectively. In the absence of any external sources of charge and current, the electromagnetic field operators satisfy the Maxwell equation:

$$\nabla \times \hat{\varvec{B}}^{ + } \left( {\varvec{r},\omega } \right) = - i\omega \mu_{0} \hat{\varvec{D}}^{ + } \left( {\varvec{r},\omega } \right) + \mu_{0} \hat{\varvec{J}}^{ + } \left( {\varvec{r},\omega } \right),$$
(3)

where \(\mu_{0}\) is the permeability of the free space, and because of the absorptive nature of the medium, the noise current density operator \(\hat{\varvec{J}}^{ + } \left( {\varvec{r},\omega } \right)\) is introduced. The electric field operator \(\hat{\varvec{E}}^{ + } \left( {\varvec{r},\omega } \right)\) and the displacement operator \(\hat{\varvec{D}}^{ + } \left( {\varvec{r},\omega } \right)\) are related in the frequency domain by the simple relation

$$\hat{\varvec{D}}^{ + } \left( {\varvec{r},\omega } \right) = \varepsilon_{0} \varepsilon \left( {\varvec{r},\omega } \right)\hat{\varvec{E}}^{ + } \left( {\varvec{r},\omega } \right),$$
(4)

where \(\varepsilon_{0}\) is the vacuum electric permittivity. The negative frequency parts are obtained by taking the Hermitian conjugate of these equations. In a gauge with zero scalar potential, the electric and the magnetic field operators are related to the vector potential operator as

$$\hat{\varvec{E}}^{ + } \left( {\varvec{r},\omega } \right) = i\omega \hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right),$$
(5)
$$\hat{\varvec{B}}^{ + } \left( {\varvec{r},\omega } \right) = \nabla \times \hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right).$$
(6)

Using Eqs. (4), (5) and (6) in (3),

$$\nabla \times \left( {\nabla \times \hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right)} \right) - \varepsilon \left( {\varvec{r},\omega } \right)q^{2} \hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right) = \frac{1}{{\varepsilon_{0} c^{2} }}\hat{\varvec{J}}^{ + } \left( {\varvec{r},\omega } \right),$$
(7)

where \(q = \omega /c\) and substitution \(\mu_{0} = 1/\varepsilon_{0} c^{2}\) is done. This equation may be solved using the Green function technique. In frequency domain, the vector potential Green function tensor \(G_{\alpha \beta }\) is defined by

$$\hat{A}_{\alpha }^{ + } \left( {\varvec{r},\omega } \right) = \mathop \sum \limits_{\beta } \int d^{3} \varvec{r}'G_{\alpha \beta } \left( {\varvec{r},\varvec{r^{\prime}},\omega } \right)\hat{J}_{\beta }^{ + } \left( {\varvec{r}',\omega } \right).$$
(8)

Using this definition in (7), it can be shown that \(G_{\alpha \beta }\) components satisfy the following nine partial differential equations:

$$\mathop \sum \limits_{\mu } \left(\varepsilon \left( {\varvec{r},\omega } \right)q^{2} \delta_{\lambda \mu } - \frac{{\delta^{2} }}{{\partial x_{\mu } \partial x_{\lambda } }} + \delta_{\lambda \mu } \nabla^{2} \right)G_{\mu \nu } \left( {\varvec{r},\varvec{r^{\prime}},\omega } \right) = - \frac{1}{{\varepsilon_{0} c^{2} }}\delta_{\lambda \nu } \delta \left( {\varvec{r} - \varvec{r^{\prime}}} \right).$$
(9)

In this formalism, the field commutation relations are obtained from the assumed noise current density operator commutation relations:

$$\left[ {\hat{J}_{\alpha }^{ + } \left( {\varvec{r},\omega } \right),\hat{J}_{\beta }^{ - } \left( {\varvec{r}',\omega '} \right)} \right] = \alpha \left( {\varvec{r},\omega } \right)\delta_{\alpha \beta } \delta \left( {\varvec{r} - \varvec{r^{\prime}}} \right)\delta \left( {\omega - \omega^{\prime}} \right),$$
(10)
$$\left[ {\hat{J}_{\alpha }^{ + } \left( {\varvec{r},\omega } \right),\hat{J}_{\beta }^{ + } \left( {\varvec{r}',\omega '} \right)} \right] = \left[ {\hat{J}_{\alpha }^{ - } \left( {\varvec{r},\omega } \right),\hat{J}_{\beta }^{ - } \left( {\varvec{r}',\omega '} \right)} \right] = 0,$$
(11)

where

$$\alpha \left( {\varvec{r},\omega } \right) = 2\varepsilon_{0} \hbar \omega^{2} \varepsilon_{i} \left( {\varvec{r},\omega } \right).$$
(12)

3 The Green function

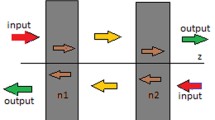
We choose the origin at the center of the slab (with thickness \(a\)) and the z-axis perpendicular to it. We label the left- and right-hand sides of the slab as 1 and 3 and the slab region as 2 (as shown in Fig. 1).

Fig. 1
figure 1

A dielectric slab in vacuum

Full size image

An effective complex refractive index \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}\) is defined as

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} \left( {k_{\parallel } ,z,\omega } \right) = \sqrt {\varepsilon \left( \omega \right) - k_{\parallel }^{2} /q^{2} } = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta } + i\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa } ,$$
(13)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta }\) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa }\) are the real and imaginary parts of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}\). Note that \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}\) is not identical with refractive index \(n\), unless \(k_{\parallel }\) = 0, which corresponds to normal incidence. Since for the vacuum, \(\varepsilon \left( \omega \right) = 1\), the effective refractive index of the free space is

$$n_{0} = \sqrt {1 - k_{\parallel }^{2} /q^{2} } .$$
(14)

Considering the geometrical symmetry of the problem, by applying the Fourier transforms

$$G_{\alpha \beta } \left( {\varvec{r},\varvec{r^{\prime}},\omega } \right) = \frac{1}{2\pi }\int d^{2} \varvec{k}_{\parallel } G_{\alpha \beta } \left( {\varvec{k}_{\parallel } ,\omega ,z,z^{\prime}} \right)e^{{i\varvec{k}_{\parallel } .\left( {\varvec{X}_{\parallel } - \varvec{X}_{\parallel }^{ '} } \right)}} ,$$
(15)
$$\delta \left( {\varvec{r} - \varvec{r^{\prime}}} \right) = \frac{1}{{\left( {2\pi } \right)^{2} }}\delta \left( {z - z^{\prime}} \right)\int d^{2} \varvec{k}_{\parallel } e^{{i\varvec{k}_{\parallel } .\left( {\varvec{X}_{\parallel } - \varvec{X}_{\parallel }^{ '} } \right)}} ,$$
(16)

the partial differential Eq. (9) are converted into a set of nine ordinary differential equations in z variable. To decrease the number of off-diagonal components of the Green function tensor \(\varvec{G}\left( {\varvec{k}_{\parallel } ,\omega ,z,z^{\prime}} \right)\), the rotation matrix S \(\left( {\varvec{k}_{\parallel } } \right)\) (the matrix that rotate the vector \(\left( {k_{x} , k_{y} , 0} \right)\) into \(\left( {k_{\parallel } , 0, 0} \right)\)) and auxiliary Green tensor \(\varvec{g}\left( {{\text{k}}_{\parallel } ,\omega ,z,z^{\prime}} \right)\) are introduced as follows:

$${\mathbf{S}}\left( {\varvec{k}_{\parallel } } \right) = \frac{1}{{k_{\parallel } }}\left[ {\begin{array}{*{20}c} {k_{x} } & {\quad k_{y} } & {\quad 0} \\ { - k_{y} } & {\quad k_{x} } & {\quad 0} \\ 0 & {\quad 0} & {\quad k_{\parallel } } \\ \end{array} } \right],$$
(17)
$$\varvec{g}\left( {k_{\parallel } ,\omega ,z,z^{\prime}} \right) = \varvec{ S}\left( {\varvec{k}_{\parallel } } \right)\varvec{G}\left( {\varvec{k}_{\parallel } ,\omega ,z,z^{\prime}} \right)\varvec{S}^{ - 1} \left( {\varvec{k}_{\parallel } } \right).$$
(18)

It can be shown that the four components \(g_{xy} , g_{yx} , g_{yz}\) and \(g_{zy}\) satisfy four homogeneous differential equations (and, therefore, for simplicity we can set these functions zero), while the other five components satisfy the five inhomogeneous differential equations [25]:

$$\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }} + \left( {q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)^{2} } \right)g_{xx} \left( {k_{\parallel } ,\omega ,z,z '} \right) = - \frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}{{2\pi \varepsilon_{0} \varepsilon c^{2} }}\delta \left( {z - z'} \right),$$
(19)
$$\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }} + \left( {q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)^{2} } \right)g_{yy} \left( {k_{\parallel } ,\omega ,z,z '} \right) = - \frac{1}{{2\pi \varepsilon_{0} c^{2} }}\delta \left( {z - z'} \right) ,$$
(20)
$$\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}z^{2} }} + \left( {q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)^{2} } \right)g_{xz} \left( {k_{\parallel } ,\omega ,z,z'} \right) = - \frac{{ik_{\parallel } }}{{2\pi \varepsilon_{0} c^{2} \varepsilon q^{2} }}\frac{\text{d}}{{{\text{d}}z}}\delta \left( {z - z'} \right),$$
(21)
$$g_{zx} \left( {k_{\parallel } ,\omega ,z,z'} \right) = \frac{{ik_{\parallel } }}{{q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}\frac{\text{d}}{{{\text{d}}z}}g_{zx} \left( {k_{\parallel } ,\omega ,z,z'} \right),$$
(22)
$$g_{zz} \left( {k_{\parallel } ,\omega ,z,z'} \right) = \frac{{ik_{\parallel } }}{{q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}\frac{\text{d}}{{{\text{d}}z}}g_{xz} \left( {k_{\parallel } ,\omega ,z,z'} \right) - \frac{1}{{2\pi \varepsilon_{0} c^{2} q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}\delta \left( {z - z^{\prime}} \right).$$
(23)

It is seen that only \(g_{xx} , g_{yy}\) and \(g_{xz}\) are needed to calculate independently, \(g_{zx}\) and \(g_{zz}\) are derived from \(g_{xx}\) and \(g_{xz} ,\) respectively. The \(g_{\alpha \beta }\) functions are assumed to be outgoing or exponentially decaying waves at \(z = \pm \infty\) (depending on the values of \(k_{\parallel }\) and \(q\)). The boundary conditions at the slab interfaces are obtained by imposing the continuity of the tangential components of \(\hat{\varvec{E}}\) and \(\hat{\varvec{H}}\), and normal components of \(\hat{\varvec{D}}\) and \(\hat{\varvec{B}}\). It can be shown that the following functions have to be continuous at the interfaces of the slab [25]:

$$g_{yy} ,\quad g_{xx} ,\quad g_{xz} ,\quad \frac{\text{d}}{{{\text{d}}z}}g_{yy} ,\quad \frac{\varepsilon }{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}\frac{\text{d}}{{{\text{d}}z}}g_{xx} ,\quad \frac{\varepsilon }{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{2} }}\frac{\text{d}}{{{\text{d}}z}}g_{xz} .$$
(24)

For evaluating the explicit forms of the field operators at the position of the atom [placed in domain (1)], we need to determine all auxiliary \(g_{\alpha \beta }\) components when the observation point \(\varvec{r}\) is in domain (1). Initially, the slab is assumed to be in a medium with relative electric permittivity \(\varepsilon '\). For the slab placed in vacuum, the field operators are obtained by imposing the limit \(\varepsilon ' \to 1\) on the resulted expressions:

$$\varepsilon^{\prime} = \varepsilon_{r}^{\prime} + i\varepsilon_{i}^{\prime} = (\varepsilon_{r}^{\prime} + i2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta } '\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa } ') \to 1\quad \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} ' \to n_{0} .$$
(25)

These relations are assumed to be equivalent with

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta } ' \to n_{0} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa } ' \to 0\;{\text{and}}\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{\prime} \to n_{0 } .$$
(26)

Using the two relations

$$\left( {\frac{{d^{2} }}{{dz^{2} }} + \alpha^{2} } \right)\frac{1}{2i\alpha }e^{{i\alpha \left| {z - z'} \right|}} = \delta \left( {z - z^{\prime}} \right) ,$$
(27)
$$\left( {\frac{{d^{2} }}{{dz^{2} }} + \alpha^{2} } \right)\frac{1}{2}e^{{i\alpha \left| {z - z^{\prime}} \right|}} {\text{sgn}}\left( {{\text{z}} - {\text{z}}^{\prime } } \right) = \frac{d}{dz}\delta \left( {z - z'} \right) ,$$
(28)

and the mentioned boundary conditions, the differential Eqs. (19), (20) and (21) can be solved easily. The required \(g_{\alpha \beta }\) functions are obtained as

for \(\varvec{z}, \varvec{z^{\prime}} < - a/2\):

$$\begin{aligned} g_{\alpha \beta } & = \frac{i}{{4\pi \varepsilon_{0} c^{2} \varepsilon^{\prime}q}}\varOmega_{\alpha \beta } \left[ {R_{m} e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} \left( {z + z\prime } \right)}} + f_{\alpha \beta } \left( {z - z^{\prime } } \right)e^{{iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} \left| {z - z^{\prime}} \right|}} } \right] \\ & \quad - \frac{1}{{2\pi \varepsilon_{0} c^{2} q^{2} \varepsilon^{\prime}}}\delta_{\alpha z} \delta_{\beta z} \delta \left( {z - z^{\prime}} \right) \\ \end{aligned} ,$$
(29)

where

$$\begin{array}{*{20}c} {{\varvec{\Omega}} = \left[ {\begin{array}{*{20}c} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ \prime} } & 0 & { - \frac{{{\text{k}}_{\parallel } }}{q}} \\ 0 & {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}} & 0 \\ {\frac{{{\text{k}}_{\parallel } }}{q}} & 0 & { - \frac{{{\text{k}}_{\parallel }^{2} }}{{q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}} \\ \end{array} } \right],} & {\varvec{f} = \left[ {\begin{array}{*{20}c} 1 & 0 & {sgn\left( {z - z^{\prime}} \right)} \\ 0 & 1 & 0 \\ { - sgn\left( {z - z^{\prime}} \right)} & 0 & { - 1} \\ \end{array} } \right]} \\ \end{array} .$$
(30)

For \(\begin{array}{*{20}c} {\varvec{z} < - a/2} & { - a/2 < \varvec{z^{\prime}} < a/2} \\ \end{array}\):

$$g_{\alpha \beta } = \frac{i}{{4\pi \varepsilon_{0} c^{2} \varepsilon^{\prime}q}}\varOmega_{\alpha \beta }^{ '} \left[ { \pm B_{m} e^{{ - iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}} \right)}} + C_{m} e^{{ - iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}} \right)}} } \right] .$$
(31)

Here the lower sign stands for \(g_{xz}\) and \(g_{zz}\),

$${\text{for}}\;\varvec{z} < - a/2\;a/2 < z ' :\quad g_{\alpha \beta } = \frac{i}{{4\pi \varepsilon_{0} c^{2} \varepsilon^{\prime}q}}\varOmega_{\alpha \beta }^{\prime \prime } T_{d} e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} \left( {z - z^{\prime}} \right)}} ,$$
(32)

where

$${\varvec{\Omega}}^{\prime } = \left[ {\begin{array}{*{20}c} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ \prime} } & 0 & { - \frac{{{\text{k}}_{\parallel } }}{q}\frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} }}} \\ 0 & {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}} & 0 \\ {\frac{{{\text{k}}_{\parallel } }}{q}} & 0 & { - \frac{{{\text{k}}_{\parallel }^{2} }}{{q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} }}} \\ \end{array} } \right],\quad {\varvec{\Omega}}^{\prime \prime } = \left[ {\begin{array}{*{20}c} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ \prime} } & 0 & {\frac{{{\text{k}}_{\parallel } }}{q}} \\ 0 & {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ \prime} }}} & 0 \\ {\frac{{{\text{k}}_{\parallel } }}{q}} & 0 & {\frac{{{\text{k}}_{\parallel }^{2} }}{{q^{2} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ \prime} }}} \\ \end{array} } \right] .$$
(33)

Here \(R_{m}\) and \(T_{m}\) are the slab reflection and transmission coefficient, respectively.

$$R_{m} = \frac{{r_{m} \left( {e^{{2iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} a}} - 1} \right)e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} a }} }}{{1 - r_{m}^{2} e^{{2iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} a}} }},\quad T_{m} = \frac{{4N_{m} }}{{\left( {N_{m} + 1} \right)^{2} }}\frac{{e^{{iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a}} }}{{1 - r_{m}^{2} e^{{2iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} a}} }}.$$
(34)

The coefficients \(B_{m}\) and \(C_{m}\) are related to these coefficients by

$$B_{m} = \frac{1}{{t_{m} }}T_{m} e^{{ - iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} = \frac{1}{{t_{m} }}\left[ {r_{m} R_{m} e^{{iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} + e^{{iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} } \right] ,$$
(35)
$$C_{m} = \frac{{r_{m} }}{{t_{m} }}T_{m} e^{{iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} = \frac{1}{{t_{m} }}\left[ {R_{m} e^{{ - iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} + r_{m} e^{{iq\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} } \right)a/2}} } \right] .$$
(36)

Here the interface reflection and transmission coefficients \(r_{m}\) and \(t_{m}\) are

$$\begin{array}{*{20}c} {r_{m} = \frac{{N_{m} - 1}}{{N_{m} + 1}}} & {t_{m} = \frac{{2N_{m} }}{{N_{m} + 1}}} \\ \end{array} ,$$
(37)

and

$$N_{m} = \left\{ {\begin{array}{*{20}c} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} /\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{\prime} } & {{\text{for}}\;m = s } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{\prime} \varepsilon /\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} \varepsilon '} & {{\text{for}}\;m = d } \\ \end{array} } \right. ,$$
(38)

where m = s stands for \(g_{yy}\) and m = d stands for other \(g_{\alpha \beta }\) components. By considering this relation (38), it is clear that in \(g_{yy} ,\) the parameters \(R_{m} ,\) \(T_{m}\), \(B_{m}\) and \(C_{m}\) are not equal with those in other \(g_{\alpha \beta }\) components. In fact, only the \(g_{yy}\) component contributes to the normal polarization part, while the other components contribute to the doublet polarization part of the field operators (as we will see).

4 Electromagnetic field operators

By considering the symmetry of the problem, it is clear that the field operators have traveling nature only in the z-direction, while the propagation along the x- and y-directions can be represented as Fourier transforms in two-dimensional \(\varvec{k}\) space. Therefore, it is convenient that by imposing the two-dimensional Fourier transform on the Green tensor \(\varvec{G}\) and the noise current density \(\hat{\varvec{J}} ^{ + }\), the Green function tensor definition (8) is rewritten in the form:

$$\hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right) = \int d^{2} k_{\parallel } e^{{i\varvec{k}_{\parallel } .\varvec{X}_{\parallel } }} \mathop \int \limits_{ - \infty }^{ + \infty } dz '\varvec{G}\left( {\varvec{k}_{\parallel } ,\omega ,z,z^{\prime}} \right).\hat{\varvec{J}}^{ + } \left( {\varvec{k}_{\parallel } ,\omega , z '} \right).$$
(39)

Multiplying Eqs. (10) and (11) by \(\frac{1}{{\left( {2\pi } \right)^{2} }}e^{{ - i\varvec{k}_{\parallel .} \varvec{X}_{\parallel } }} e^{{ - i\varvec{k}_{\parallel }^{'} .\varvec{X}_{\parallel }^{'} }} d^{2} X_{\parallel } d^{2} X_{\parallel }^{'}\) and performing the required integrations, we find

$$[\hat{J}_{\alpha }^{ + } \left( { \varvec{k}_{\parallel } ,\omega , z} \right), \hat{J}_{\beta }^{ - } \left( {,\varvec{k}_{\parallel }^{ '} ,\omega^{\prime}, z '} \right) ]= \alpha \left( {z,\omega } \right)\delta_{\alpha \beta } \delta \left( {z - z^{\prime}} \right)\delta (\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{ '} )\delta \left( {\omega - \omega^{\prime}} \right),$$
(40)
$$\left[ {\hat{J}_{\alpha }^{ + } \left( {\varvec{k}_{\parallel } ,\omega , z} \right),\hat{J}_{\beta }^{ + } \left( {,\varvec{k}_{\parallel }^{ '} ,\omega^{\prime}, z^{\prime}} \right)} \right] = \left[ {\hat{J}_{\alpha }^{ - } \left( {\varvec{k}_{\parallel } , \omega , z} \right),\hat{J}_{\beta }^{ - } \left( {,\varvec{k}_{\parallel }^{ '} ,\omega^{\prime}, z^{\prime}} \right)} \right] = 0 .$$
(41)

By symmetry considerations, it is clear that the x and y components of the field operators have the same forms. But in practice, when there are some boundary interfaces, the electric field is usually decomposed into normal, parallel and longitudinal polarizations parts (with respect to the incidence plane)and each component is investigated separately. For this purpose, the rotation given by the matrix (17) is used. The net effect of this operation is the decomposition of the field operators into two parts, known as singlet and doublet parts [23, 24].

$$\hat{\varvec{A}}^{ + } \left( {\varvec{r},\omega } \right) = \hat{\varvec{A}}^{ + s} \left( {\varvec{r},\omega } \right) + \hat{\varvec{A}}^{ + d} \left( {\varvec{r},\omega } \right).$$
(42)

The singlet part corresponds to the normal polarization state of the electric field operator and arises only from the \(g_{yy}\) component. The doublet part corresponds to the sum of the parallel and the longitudinal polarization components of the electric field operator and is due to other \(g_{\alpha \beta }\) functions. It can be shown [23, 24]

$$\hat{\varvec{A}}^{ + s} \left( {\varvec{r},\omega } \right) = \int d^{2} k_{\parallel } e^{{i\varvec{k}_{\parallel } .\varvec{X}_{\parallel } }} \tilde{\varvec{e}}^{s} \left( \varvec{k} \right)\mathop \int \limits_{ - \infty }^{ + \infty } dz 'g_{yy} \left( {k_{\parallel } ,\omega ,z,z '} \right)\hat{J}_{s}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z '} \right) ,$$
(43)
$$\hat{\varvec{A}}_{\parallel }^{ + d} \left( {\varvec{r},\omega } \right) = \int d^{2} {\text{k}}_{\parallel } e^{{i\varvec{k}_{\parallel } .\varvec{X}_{\parallel } }} \tilde{\varvec{k}}_{\parallel } \mathop \int \limits_{ - \infty }^{ + \infty } dz '\left[ {g_{xx} \hat{J}_{\parallel }^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z^{\prime}} \right) + g_{xz} \hat{J}_{z}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z^{\prime}} \right)} \right],$$
(44)
$$\hat{\varvec{A}}_{z}^{ + d} \left( {\varvec{r},\omega } \right) = \int d^{2} k_{\parallel } e^{{i\varvec{k}_{\parallel } .\varvec{X}_{\parallel } }} \mathop \int \limits_{ - \infty }^{ + \infty } dz^{\prime}\left[ {g_{zx} \hat{J}_{\parallel }^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z^{\prime}} \right) + g_{zz} \hat{J}_{z}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z^{\prime}} \right)} \right].$$
(45)

Here the normal polarization vector \(\tilde{\varvec{e}}^{s} \left( \varvec{k} \right)\) and the normal component of the noise current density operator \(\hat{J}_{s}^{ + }\) are given by

$$\tilde{\varvec{e}}^{s} \left( \varvec{k} \right) = \varvec{ }\frac{1}{{\varvec{k}_{\parallel } }}\left( {k_{\varvec{y}} , - k_{\varvec{x}} ,0} \right) ,$$
(46)
$$\hat{J}_{s}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z'} \right) = \tilde{\varvec{e}}^{s} \left( \varvec{k} \right).\hat{J}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z'} \right) ,$$
(47)

which satisfies the commutation relation

$$\left[ {\hat{J}_{s}^{ + } \left( {z, \varvec{k}_{\parallel } ,\omega } \right),\hat{J}_{s}^{ - } \left( {z ',\varvec{k}_{\parallel }^{ '} ,\omega } \right) } \right] = \alpha \left( {z,\omega } \right)\delta \left( {z - z^{\prime}} \right)\delta \left( {\varvec{k}_{\parallel } , - \varvec{k}_{\parallel }^{ '} } \right)\delta \left( {\omega - \omega^{\prime}} \right).$$
(48)

The \(\hat{J}_{\parallel }^{ + }\) component of the noise current density operator is given by

$$\hat{J}_{\parallel }^{ + } ( \varvec{k}_{\parallel } ,\omega ,z') = \hat{\varvec{k}}_{\parallel } .\hat{J}^{ + } \left( { \varvec{k}_{\parallel } ,\omega ,z'} \right),$$
(49)

where \(\hat{\varvec{k}}_{\parallel } = \left( {k_{x} /k_{\parallel } , k_{y} /k_{\parallel } , 0 } \right)\).

It is convenient to define the \(\hat{f}_{s} \left( {z, \varvec{k}_{\parallel } ,\omega } \right)\), \(\hat{f}_{\parallel } \left( {z, \varvec{k}_{\parallel } ,\omega } \right)\) and \(\hat{f}_{z} \left( {z, \varvec{k}_{\parallel } ,\omega } \right)\) operators as follows:

$$\hat{f}_{s} = \frac{1}{\sqrt \alpha }\hat{J}_{s}^{ + } , \begin{array}{*{20}c} {\hat{f}_{\parallel } = \frac{1}{\sqrt \alpha }\hat{J}_{\parallel }^{ + } ,} & {\hat{f}_{z} = \frac{1}{\sqrt \alpha }\hat{J}_{z}^{ + } } \\ \end{array} .$$
(50)

The commutation relations of these operators can be derived from commutation relations (40) and (41). By considering the polarization vector (46), and singlet part vector potential (43),

$$\hat{A}_{z}^{ + s} \left( {\varvec{r},\omega } \right) = 0.$$
(51)

Thus, the z component of total vector potential is equal to the vector potential z component of the doublet system.

5 Field operators and commutation relations

For spontaneous emission rate determination of an excited atom placed in region (1), the electric field operator in \(z < - a/2\) region is only needed. Substituting the explicit forms of the required \(g_{\alpha \beta }\) components (given in relations (29), (31) and (32)), in Eqs. (43), (44) and (45), using the definitions (12) and (50), then applying the limit \(\varepsilon ' \to 1\) to the resulted expressions, the positive frequency part of the vector potential operator for the singlet and doublet systems are obtained as follows:

$$\hat{A}_{i}^{ + m} \left( {\varvec{r},\omega } \right) = \sqrt {\frac{\hbar }{{8\pi^{2} \varepsilon_{0} c^{2} q}}} \int d^{2} \varvec{k}_{\parallel } e^{{i\varvec{k}_{\parallel } .\varvec{X}_{\parallel } }} X_{\varvec{m}} \tilde{e}_{i}^{m} \left( \varvec{k} \right)\left[ { \pm \hat{a}_{R1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right)e^{{iqn_{0} z}} + \hat{a}_{L1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right)e^{{ - iqn_{0} z}} } \right],$$
(52)

where m = s and d refer to singlet and doublet parts, respectively; the lower sign refer to the z component of the doublet part, \(X_{m}\) and the doublet polarization vector \(\tilde{e}_{i}^{d} \left( \varvec{k} \right)\) are defined by

$$X_{m} = \left\{ {\begin{array}{*{20}c} {1/\sqrt {n_{0} } } & {{\text{for}}\;m = s} \\ {\sqrt {n_{0} } } & {{\text{for}}\;m = d} \\ \end{array} } \right\} ,$$
(53)
$$\tilde{\varvec{e}}^{d} \left( \varvec{k} \right) = \left( { k_{x} /k_{\parallel } , k_{y} /k_{\parallel } , k_{\parallel } /n_{o} q} \right) .$$
(54)

The left-going annihilation operator \(\hat{a}_{L1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right)\) is given by

$$\hat{a}_{L1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right) = \left[ {R_{m} \hat{a}_{R1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right) + T_{m} \hat{a}_{L3}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right) + \hat{F}_{L}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right)} \right] .$$
(55)

The singlet and doublet incoming annihilation operators are defined by

$$\hat{a}_{R1}^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) = {\text{Lim}}_{{\varepsilon^{\prime} \to 1}} i\sqrt {\frac{{\varepsilon_{i}^{ '} q}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}} \mathop \int \limits_{ - \infty }^{ - a/2} dz^{\prime}e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z^{\prime}}} \hat{f}_{s} \left( {z ', \varvec{k}_{\parallel } ,\omega } \right),$$
(56)
$$\hat{a}_{L3}^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) = {\text{Lim}}_{{\varepsilon^{\prime} \to 1}} i\sqrt {\frac{{\varepsilon_{i}^{ '} q}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}} \mathop \int \limits_{{{\text{a}}/2}}^{ + \infty } dz^{\prime}e^{{iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z^{\prime}}} \hat{f}_{s} \left( {z^{\prime}, \varvec{k}_{\parallel } ,\omega } \right),$$
(57)
$$\hat{a}_{R1}^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right) = {\text{Lim}}_{{\varepsilon^{\prime} \to 1}} i\sqrt {q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} \varepsilon_{i}^{ '} } \mathop \int \limits_{ - \infty }^{ - a/2} dz^{\prime}e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z^{\prime}}} \left( {\hat{f}_{\parallel } - \frac{{k_{\parallel } }}{{q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}\hat{f}_{z} } \right),$$
(58)
$$\hat{a}_{L3}^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right) = {\text{Lim}}_{{\varepsilon^{\prime} \to 1}} i\sqrt {q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} \varepsilon_{i}^{ '} } \mathop \int \limits_{{{\mathbf{a}}/2}}^{ + \infty } dz^{\prime}e^{{iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} z^{\prime}}} \left( {\hat{f}_{\parallel } + \frac{{k_{\parallel } }}{{q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}^{ '} }}\hat{f}_{z} } \right).$$
(59)

Using definition (50), commutation relations (40) and (48), and applying the limit (26), it can be shown that the incoming annihilation operators \(\hat{a}_{R1}^{m}\) and \(\hat{a}_{L3}^{m}\) satisfy the following commutation relations:

$$\left[ {\hat{a}_{{R1}}^{m} \left( {\user2{k}_{\parallel } ,\omega } \right),{\text{~}}\hat{a}_{{R1}}^{{m + }} \left( {\user2{k}_{\parallel }^{'} ,\omega ^{\prime}} \right)} \right] = \left[ {\hat{a}_{{L3}}^{m} \left( {\user2{k}_{\parallel } ,\omega } \right),{\text{~}}\hat{a}_{{L3}}^{{m + }} \left( {\user2{k}_{\parallel }^{'} ,\omega ^{\prime}} \right)} \right] = \delta \left( {\user2{k}_{\parallel } - \user2{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega {\text{'}}} \right).$$
(60)

The left-going noise operator \(\hat{F}_{L}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right)(\) which is due to absorptive nature of the slab) is defined by

$$\hat{F}_{L}^{\varvec{s}} \left( {\varvec{k}_{\parallel } ,\omega } \right) = i\sqrt {\frac{{\varepsilon_{i} q}}{{n_{0} }}} \mathop \int \limits_{ - a/2}^{a/2} dz '\left[ {B_{s} e^{{iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}}} + C_{s} e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}}} } \right]\hat{f}_{s} \left( {z ', \varvec{k}_{\parallel } ,\omega } \right) ,$$
(61)
$$\hat{F}_{L}^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right) = i\sqrt {qn_{0} \varepsilon_{i} } \mathop \int \limits_{ - a/2}^{a/2} dz '\left[ {\hat{f}_{{n^{ + } }} B_{d} e^{{iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}}} + \hat{f}_{{n^{ - } }} C_{d} e^{{ - iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} z^{\prime}}} } \right] ,$$
(62)

where

$$\hat{f}_{{n^{ \pm } }} \left( {z,\varvec{k}_{\parallel } ,\omega } \right) = \hat{f}_{\parallel } \left( {z,\varvec{k}_{\parallel } ,\omega } \right) \pm \frac{{k_{\parallel } }}{{q\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} }}\hat{f}_{z} \left( {z,\varvec{k}_{\parallel } ,\omega } \right),$$
(63)

where \(\hat{f}_{s}\) and \(\hat{f}_{{n^{ \pm } }}\) satisfy the commutation relations

$$\left[ {\hat{f}_{s} \left( {z, \varvec{k}_{\parallel } ,\omega } \right) , \hat{f}_{s}^{ + } \left( {z',\varvec{k}_{\parallel }^{'} ,\omega } \right)} \right] = \delta \left( {z - z^{\prime}} \right)\delta \left( {\varvec{k}_{\parallel } , - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right),$$
(64)
$$[\hat{f}_{{n^{ \pm } }} \left( {z,\varvec{k}_{\parallel } ,\omega } \right),\hat{f}_{{n^{ \pm } }}^{ + } \left( {z ',\varvec{k}_{\parallel }^{'} ,\omega '} \right)] = \varGamma^{ + } \delta \left( {\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right)\delta \left( {z - z^{\prime}} \right) ,$$
(65)
$$[\hat{f}_{{n^{ \pm } }} \left( {z,\varvec{k}_{\parallel } ,\omega } \right),\hat{f}_{{n^{ \mp } }}^{ + } \left( {z ',\varvec{k}_{\parallel }^{'} ,\omega '} \right)] = \varGamma^{ - } \delta \left( {\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right)\delta \left( {z - z^{\prime}} \right) ,$$
(66)

where

$$\varGamma^{ \pm } = 1 \pm \frac{{k_{\parallel }^{2} }}{{q^{2} \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right|^{2} }}.$$
(67)

Using relations (35) and (36), commutation relations (64), (65) and (66), after some manipulation it can be shown

$$\left[ {\hat{F}_{L}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right), \hat{F}_{L}^{m + } \left( {\varvec{k}_{\parallel }^{'} ,\omega^{\prime}} \right)} \right] = \left( {1 - \left| {R_{m} } \right|^{2} - \left| {T_{m} } \right|^{2} } \right)\delta \left( {\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right).$$
(68)

The term \(\left( {1 - \left| {R_{m} } \right|^{2} - \left| {T_{m} } \right|^{2} } \right)\) can be interpreted as the absorption probability of a single incident photon (with the frequency \(\omega\) and propagation vector \(\varvec{k}_{\parallel }\)) [26].

Using definition (55), commutation relations (60) and (68), and since in the definitions of \(\varvec{ }\hat{a}_{R1}^{m}\), \(\hat{a}_{L3}^{m}\) and \(\hat{F}_{L}^{m}\), the components of the operator \(\hat{\varvec{f}}\) are associated with different regions of space, the commutation relations between the right- and left-going annihilation operator \(\hat{a}_{R1}^{m}\) and \(\hat{a}_{L1}^{m}\) are obtained as

$$[\hat{a}_{L1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right),\hat{a}_{R1}^{m + } \left( {\varvec{k}_{\parallel }^{'} ,\omega '} \right)] = [\hat{a}_{R1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right),\hat{a}_{L1}^{m + } \left( {\varvec{k}_{\parallel }^{'} ,\omega '} \right)]^{ *} = R_{m} \delta \left( {\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right) ,$$
(69)

and also

$$[\hat{a}_{L1}^{m} \left( {\varvec{k}_{\parallel } ,\omega } \right),\hat{a}_{L1}^{m + } \left( {\varvec{k}_{\parallel }^{'} ,\omega '} \right)] = \delta \left( {\varvec{k}_{\parallel } - \varvec{k}_{\parallel }^{'} } \right)\delta \left( {\omega - \omega^{\prime}} \right).$$
(70)

Note, it is necessary to take limiting procedures (25) and (26) as equivalent to each other. On the other hand, if in applying the limit \(\varepsilon_{i}^{'} = 2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta } '\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa } ' \to 0\), the condition \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\eta } ' \to 0\) is chosen (instead of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\kappa } ' \to 0\)), then fundamental commutation relations (60) vanishes [24] (which is not acceptable). Therefore, the imaginary part of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} '\) approaches zero, now, \(n_{0}\) which is the limit case of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} '\) has to be real. As a result, from definition (14), we find

$$k_{\parallel } \le q .$$
(71)

6 Spontaneous emission rate

The spontaneous emission rate of an excited atom (in electric dipole approximation) is usually computed via Fermi’s golden rule [27]:

$$\varGamma = \frac{2\pi }{{\hbar^{2} }}\mathop \sum \limits_{f} \left| {f |\varvec{p}.\hat{\varvec{E}}\left( {\varvec{r}_{0} ,t} \right) |0} \right|^{2} \delta \left( {\omega_{f} - \omega_{0} } \right) ,$$
(72)

where \(\varvec{r}_{0}\) is the position, \(\omega_{0}\) is the transition frequency and \(\varvec{p}\) denotes the matrix element of the electric dipole operator (\(\hat{\varvec{p}} = e\hat{\varvec{r}}\)) between the excited and ground state of the atom. The ket \(|0\) is the vacuum state and \(|f\) states are single-photon final states of the electromagnetic field with frequency \(\omega_{f}\) equal to \(\omega_{0}\). Writing the electric field in terms of its positive and negative frequency components (using (2)) and applying the completeness of the \(|f\) states, we find

$$\varGamma = \frac{1}{{\hbar^{2} }}\mathop \int \limits_{0}^{ + \infty } d\omega \mathop \int \limits_{0}^{ + \infty } d\omega^{\prime}0\left| {\left( {\varvec{p}.\hat{\varvec{E}}^{ + } \left( {\varvec{r}_{0} ,\omega } \right)} \right)\left( {\varvec{p}.\hat{\varvec{E}}^{ - } \left( {\varvec{r}_{0} ,\omega '} \right)} \right)} \right|0e^{{ - i\left( {\omega - \omega^{\prime}} \right)t}} \delta \left( {\omega_{f} - \omega_{0} } \right) .$$
(73)

Since in this equation, the integrals are over modes which frequencies \(\omega\) and \(\omega '\) equal to \(\omega_{f} = \omega_{0}\), for atoms with electric dipole moment in \(\alpha\)-direction, the spontaneous emission rate is given by

$$\varGamma_{\alpha } = \frac{{p^{2} }}{{\hbar^{2} }}\mathop \int \limits_{0}^{ + \infty } d\omega \mathop \int \limits_{0}^{ + \infty } d\omega '0 |\hat{E}_{\alpha }^{ + } \left( {\varvec{r}_{0} ,\omega } \right)\hat{E}_{\alpha }^{ - } \left( {\varvec{r}_{0} ,\omega '} \right) |0 \delta \left( {\omega - \omega_{0} } \right) .$$
(74)

By choosing the gauge with zero scalar potential and writing the vector potential operator as the sum of singlet and doublet polarizations

$$\varGamma_{\alpha } = \frac{{p^{2} }}{{\hbar^{2} }}\mathop \sum \limits_{m} \mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega '\omega '0 |\hat{A}_{\alpha }^{m + } \left( {\varvec{r}_{0} ,\omega } \right)\hat{A}_{\alpha }^{m - } \left( {\varvec{r}_{0} ,\omega '} \right) |0\delta \left( {\omega - \omega_{0} } \right) .$$
(75)

Since \(\hat{A}_{\alpha }^{m + }\) and \(\hat{A}_{\alpha }^{m - }\) contain the annihilation and the creation operators, respectively, \(\varGamma_{\alpha }\) can be written in terms of vector potential commutation relations as

$$\varGamma_{\alpha } = \frac{{p^{2} }}{{\hbar^{2} }}\mathop \sum \limits_{m} \mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega '\omega '[\hat{A}_{\alpha }^{m + } \left( {\varvec{r}_{0} ,\omega } \right),\hat{A}_{\alpha }^{m - } \left( {\varvec{r}_{0} ,\omega '} \right)]\delta \left( {\omega - \omega_{0} } \right) = \mathop \sum \limits_{m} \varGamma_{\alpha }^{m} .$$
(76)

For the atoms with the electric dipole moments in the x-direction (parallel with the slab), using normal polarization vector (46) and vector potential operator (52), the contribution of the singlet part in spontaneous emission rate is given by

$$\begin{aligned} \varGamma_{x}^{s} & = \frac{{p^{2} }}{{\hbar^{2} }}\mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega^{\prime}\omega^{\prime}[\hat{A}_{x}^{s + } \left( {\varvec{r}_{0} , \omega } \right),\hat{A}_{x}^{s - } \left( {\varvec{r}_{0} , \omega^{\prime}} \right)]\delta \left( {\omega - \omega_{0} } \right), \\ & = \frac{{p^{2} }}{{8\pi^{2} \varepsilon_{0} \hbar c\omega }}\mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega^{\prime}\omega^{\prime}\int d^{2} k_{\parallel } \int d^{2} k_{\parallel }^{ '} \frac{{k_{y}^{2} }}{{k_{\parallel }^{2} }}\frac{1}{{n_{0} }} \\ & \quad \times \left\{ {\left[ {\hat{a}_{R1 }^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) , \hat{a}_{R1 }^{s + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right] + \left[ {\hat{a}_{L1 }^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) , \hat{a}_{L1 }^{s + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right] } \right. \\ & \quad \left. { + \left[ {\hat{a}_{R1 }^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) , \hat{a}_{L1 }^{s + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right]{\text{e}}^{{2iqn_{0} z_{0} }} + \left[ {\hat{a}_{L1 }^{s} \left( {\varvec{k}_{\parallel } ,\omega } \right) ,\hat{a}_{R1 }^{s + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right]{\text{e}}^{{ - 2iqn_{0} z_{0} }} } \right\}\delta \left( {\omega - \omega_{0} } \right). \\ \end{aligned}$$
(77)

Using commutation relations (60), (69) and (70)

$$\varGamma_{x}^{s} = \frac{{p^{2} q_{0} }}{{8\pi^{2} \varepsilon_{0} \hbar }}\int d^{2} k_{\parallel } \frac{{k_{y}^{2} }}{{k_{\parallel }^{2} }}\frac{1}{{n_{0} }}\left[ {2 + (R_{s} e^{{ - 2iq_{0} n_{0} z_{0} }} + c.c} \right)] .$$
(78)

Performing the angular integration and applying condition (71)

$$\varGamma_{x}^{s} = \frac{3}{4}\varGamma_{0} \mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } {\text{k}}_{\parallel } \frac{1}{{q_{0}^{2} n_{0} }}\left[ {1 + {\text{Rel}}\left( {R_{s} e^{{ - 2iq_{0} n_{0} z_{0} }} } \right)} \right],$$
(79)

where \(\varGamma_{0}\) is the free space spontaneous emission rate and is given by

$$\varGamma_{0} = \frac{{p^{2} q_{0}^{3} }}{{3\pi \epsilon_{0} \hbar }}.$$
(80)

In a similar manner, using relations (52), (53), (54), commutation relations (60), (69), (70) and condition (71), the contribution of the doublet part in spontaneous emission rate is given by

$$\varGamma_{x}^{d} = \frac{3}{4}\varGamma_{0} \mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } {\text{k}}_{\parallel } \frac{{n_{0} }}{{q_{0}^{2} }}\left[ {1 + {\text{Rel}}\left( {R_{d} e^{{ - 2iq_{0} n_{0} z_{0} }} } \right)} \right] .$$
(81)

Therefore,

$$\Gamma _{x} = \frac{3}{4}\Gamma _{0} \frac{1}{{q_{0}^{2} }}\mathop \smallint \limits_{0}^{{q_{0} }} dk_{\parallel } k_{\parallel } \mathop \sum \limits_{{\text{m}}} {\text{X}}_{{\text{m}}}^{2} \left[ {1 + {\text{Rel}}\left( {R_{m} e^{{ - 2iq_{0} n_{0} z_{0} }} } \right)} \right]$$
(82)

Considering the symmetry of the problem, it is clear that \(\varGamma_{x} = \varGamma_{y}\).

For the atom with the electric dipole moments in z-directions (perpendicular to the slab), considering (51) we have

$$\varGamma_{z} = \frac{{p^{2} }}{{\hbar^{2} }}\mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega '\omega '[\hat{A}_{z}^{d + } \left( {\varvec{r}_{0} ,\omega } \right),\hat{A}_{z}^{d - } \left( {\varvec{r}_{0} ,\omega '} \right)]\delta \left( {\omega - \omega_{0} } \right) ,$$
(83)

and, therefore, using relations, (52), (53) and (54),

$$\begin{aligned} \varGamma_{\text{z}} & = \frac{{p^{2} }}{{8\pi^{2} \varepsilon_{0} \hbar c\omega }}\mathop \int \limits_{0}^{ + \infty } d\omega \omega \mathop \int \limits_{0}^{ + \infty } d\omega^{\prime}\omega^{\prime}\int d^{2} k_{\parallel } \int d^{2} k_{\parallel }^{ '} \frac{{k_{\parallel }^{2} }}{{q^{2} n_{0}^{2} }}n_{0} \\ & \quad \times \left\{ {\left[ {\hat{a}_{R1 }^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right) , \hat{a}_{R1 }^{d + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right] + \left[ {\hat{a}_{L1 }^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right) , \hat{a}_{L1 }^{d + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right]} \right. \\ & \quad - \left. {\left[ {\hat{a}_{R1 }^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right), \hat{a}_{L1 }^{d + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega^{\prime}} \right)} \right]{\text{e}}^{{2iqn_{0} z_{0} }} - \left[ {\hat{a}_{L1 }^{d} \left( {\varvec{k}_{\parallel } ,\omega } \right),\hat{a}_{R1 }^{d + } \left( {\varvec{k^{\prime}}_{\parallel } ,\omega '} \right)} \right]{\text{e}}^{{ - 2iqn_{0} z_{0} }} } \right\}\delta \left( {\omega - \omega_{0} } \right) \\ \end{aligned} .$$
(84)

Applying commutation relations (60), (69), (70) and condition (71),

$$\varGamma_{z} = \frac{3}{2}\varGamma_{0} \mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } \frac{{k_{\parallel }^{3} }}{{q_{0}^{4} n_{0} }}\left[ {1 - {\text{Rel}}\left( {R_{d} e^{{ - 2iq_{0} n_{0} z_{0} }} } \right)} \right].$$
(85)

By assumption that the probability of finding the dipole moment of the atom in x-, y-, and z-directions is equal, the average spontaneous emission rate of the atom is given by

$$\varGamma_{\text{average}} = \frac{2}{3}\varGamma_{x} + \frac{1}{3}\varGamma_{z} .$$
(86)

7 Spontaneous emission in free pace and near a conducting plate

For evaluating the spontaneous emission rate in free space, we have to apply the limit \(z_{0} \to - \infty\) to the derived emission rate expressions. In this case, the exponential terms in relations (82) and (85) fluctuate very fast and, therefore, can be set equal to zero (in average).

Now it can easily be shown that

$$\begin{array}{*{20}c} {\varGamma_{x} \to \varGamma_{0} } & {\varGamma_{z} \to \varGamma_{0} } \\ \end{array} .$$
(87)

For calculating the spontaneous emission rate near a conducting wall, we have to impose the condition \(\left| \varepsilon \right| \to \infty\). In this case, from reflection coefficient definitions (34) and (37), we find

$$R_{m} \to - e^{{ - iqn_{0} a}} .$$
(88)

Now we shift the coordinate origin to the left interface of the slab by applying

$$z_{0} \to z_{0} - a/2.$$
(89)

Imposing conditions (88) and (89) on the emission rate expressions (82) and (85) and using (53), we have

$$\varGamma_{x} \to \frac{3}{4}\varGamma_{0} \frac{1}{{q_{0}^{2} }}\mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } {\text{k}}_{\parallel } \left( {1/n_{0} + n_{0} } \right)(1 - \cos \left( {2qn_{0} z} \right),$$
(90)
$$\varGamma_{z} \to \frac{3}{2}\varGamma_{0} \mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } \frac{{k_{\parallel }^{3} }}{{q_{0}^{4} n_{0} }}\left[ {1 + { \cos }\left( {2iq_{0} n_{0} z_{0} } \right)} \right].$$
(91)

By the change of variable \(k_{\parallel } = q\sin \left( \theta \right)\) and considering the definition of \(n_{0}\) (relation (14))

$$\varGamma_{x} \to \frac{3}{4}\varGamma_{0} \mathop \int \limits_{0}^{1} dx\left( {1 + x^{2} } \right)\left[ {1 - \cos \left( {\alpha x} \right)} \right] ,$$
(92)
$$\varGamma_{z} \to \frac{3}{2}\varGamma_{0} \mathop \int \limits_{0}^{1} dx\left( {1 - x^{2} } \right)\left[ {1 + \cos \left( {\alpha x} \right)} \right] ,$$
(93)

where \(x = { \cos }\theta\) and \(\alpha = 2q_{0} z_{0}\). The integrations can be done easily and the spontaneous emission rates of the atom with electric dipole moment parallel and perpendicular to the conducting plate are obtained as follows:

$$\varGamma_{x} = \varGamma_{0} \left\{ {1 - \frac{3}{2}\left[ {\frac{{\sin \left( {2qz} \right)}}{2qz} + \frac{{\cos \left( {2qz} \right)}}{{\left( {2qz} \right)^{2} }} - \frac{{\sin \left( {2qz} \right)}}{{\left( {2qz} \right)^{3} }}} \right]} \right\} ,$$
(94)
$$\varGamma_{z} = \varGamma_{0} \left\{ {1 - 3\left[ {\frac{{\cos \left( {2qz} \right)}}{{\left( {2qz} \right)^{2} }} - \frac{{\sin \left( {2qz} \right)}}{{\left( {2qz} \right)^{3} }}} \right]} \right\} .$$
(95)

These are identical with those given in [28,29,30].

Considering the term \(\delta \left( {\omega_{f} - \omega_{0} } \right)\) in Fermi rule (72), in general, for evaluating the spontaneous emission rate, the value of dielectric function of the slab at the transition frequency \(\omega_{0}\) is needed. For this purpose, a model for the dielectric function of the slab is needed. A convenient model is the Lorentz model with a single resonance frequency \(\omega_{0}\) and damping constant \(\gamma\):

$$\varepsilon \left( \omega \right) = 1 + \frac{{\omega_{p}^{2} }}{{\omega_{0}^{2} - \omega^{2} - i\gamma \omega }} ,$$
(96)

where \(\omega_{p}\) is the plasma frequency of the dielectric. Depending on the type of the dielectric slab and the spontaneous emission frequency \(\omega_{0}\) of the atom, the related parameters \(\omega_{p}\) and \(\gamma\) have to be chosen conveniently, then by integrating relations (82) and (85) numerically, the spontaneous emission rate of the atom near the slab can be evaluated.

It is convenient to shift the origin of the coordinate to the right interface of the slab and then the typical variations of the spontaneous emission rate in the region with \(\varvec{z} > 0\) are shown.

This is done by applying the transformations \(z_{0} \to - z_{0}\) and then \(z_{0} \to z_{0} + a/2\) to emission relations (82) and (85).

$$\Gamma _{x} = \frac{3}{4}\Gamma _{0} \frac{1}{{q_{0}^{2} }}\int\limits_{0}^{{q_{0} }} d k_{\parallel } k_{\parallel } \sum\limits_{m} {X_{m}^{2} } \left[ {1 + {\text{Rel}}\left( {R_{m} e^{{2iq_{0} n_{0} z_{0} }} } \right)} \right],$$
(97)
$$\varGamma_{z} = \frac{3}{2}\varGamma_{0} \mathop \int \limits_{0}^{{q_{0} }} d{\text{k}}_{\parallel } \frac{{k_{\parallel }^{3} }}{{q_{0}^{4} n_{0} }}\left[ {1 - {\text{Rel}}\left( {R_{d} e^{{2iq_{0} n_{0} z_{0} }} } \right)} \right] ,$$
(98)

where now \(R_{m} = \frac{{r_{m} \left( {e^{{2iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} a}} - 1} \right)}}{{1 - r_{m}^{2} e^{{2iq\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} a}} }}\).

For the atom with electric dipole moment parallel and perpendicular to the slab, typical variations of the spontaneous emission rate near the slab are shown in Figs. 2 and 3, respectively.

Fig. 2
figure 2

The variations of the spontaneous emission rate near the slab, for the atom with dipole moment parallel to the slab. Vertical axis is in unit \(\varGamma_{0}\), \(a = 2\lambda\), \(\omega_{p} /\omega_{0} = 0.67\) and \(\gamma /\omega_{0} = 0.01\)

Full size image
Fig. 3
figure 3

The variations of the spontaneous emission rate near the slab, for the atom with dipole moment perpendicular to the slab. Vertical axis is in unit \(\varGamma_{0}\), \(a = 2\lambda\), \(\omega_{p} /\omega_{0} = 0.67\) and \(\gamma /\omega_{0} = 0.01\)

Full size image

8 Conclusion

In this paper, using the Green function scheme of the electromagnetic field quantization, the vector potential operator in the presence a dissipative dielectric slab is derived. The field operators can be used for investigating quantum optical processes that occur near the slab. The system is decomposed into singlet and doublet parts. The singlet part corresponds to the normal state polarization of the electric field and the doublet part corresponds to the sum of parallel and longitudinal polarizations. The explicit forms of the vector potential operators of the two parts have been obtained (Eq. (52)). The derived commutation relations between the annihilation and creation operators in domain (1) are given in relations (60), (69) and (70), where these can be used in investigating some physical problem such as spontaneous emission, lamb shift, dispersion forces. As an application to the quantization of the electromagnetic field, the spontaneous emission rate of an atom near the slab has been evaluated. The Fermi’s golden rule is used to introduce general expression (75) for the spontaneous emission rate of an excited atom or molecule in the presence of some dielectric mediums. Using vector potential operator formula (52) and commutation relations (60), (69) and (70), for atoms with the electric dipole moment parallel and perpendicular to the slab, the spontaneous emission rates are derived (as given in relations (82) and (85), respectively). For evaluating the spontaneous emission rate of a given atom near a definite slab, it is only needed to known the dielectric function of the slabs at the spontaneous emission frequency of the atom.

As two limiting cases, the spontaneous emission rates in free space and near a perfect conducting wall are calculated and their consistencies with previous work have been shown.

Choosing a Lorentz model with a single resonance frequency \(\omega_{0}\) and damping constant \(\gamma\), a typical variations of the spontaneous emission rate for the atoms with the dipole moment perpendicular and parallel with the slabs are given in Figs. 2 and 3, respectively.

As it is seen from Figs. 2 and 3, when the transition electric dipole moment of the atom is perpendicular to the slabs, the spontaneous emission rate near the slabs amplifies and when it is parallel to the slabs, the emission rate decreases. This behavior is also observed in a stronger manner when the spontaneous emission rate near a conducting wall is investigated [1]. In the same way as in the conducting wall case, one can assume that for the atom with perpendicular dipole moment, the atomic electric dipole oscillates nearly in phase with its image dipole, and in the case of the atom with parallel dipole moment, the atomic dipole and its image oscillate nearly out of phase. For points, at a distance about a few wavelengths from the slab, the spontaneous emission rate is nearly equal to the free space one. This can be attributed to the loss of the coherence between the incident and reflected waves in those points.

Using fluctuation–dissipation theorem and Kubo’s formula [31], spontaneous emission rate near the slab can only be determined by computing the vector potential of Green function of the system and without using the explicit form of field operators. This work is in progress.