1 Introduction

Optical solitons have been widely applied to long-distance communication and all-optical ultrafast switching devices after being proposed and confirmed experimentally by Hasegawa et al. [1] and Mollenauer et al. [2], respectively. So, it has attracted the concern of the research community in different fields of nonlinear optics [3,4,5,6]. The velocity, the amplitude, and the shape of the optical solitons cannot be affected in the propagation process due to the counterpoise between the self-phase modulation (SPM) effects and the group velocity dispersion (GVD) [7]. The well-known nonlinear Schrödinger (NLS) equation is regularly employed to represent pulse propagation in optical fibers and the propagation of picosecond optical solitons in monomode fibers [8]. In addition to the physical meaning of the NLS equation, many analytical solutions for this equation, such as the bright and dark solitons, have been explored in literature [9,10,11,12,13,14].

The main objective for our work is to study the following Hirota equation with variable coefficients [15]

$$\begin{aligned}&-\vartheta _2 \Xi _{TT}+i \vartheta _3(Z) \Xi _{TTT}+i \tau (Z) \Xi _T \left| \Xi \right| ^2+i \Xi _Z\nonumber \\&\quad +\gamma \left| \Xi \right| ^2 \Xi +\psi \Xi =0, \end{aligned}$$
(1)

where \(\Xi =\Xi (Z,T)\) is a complex function. Z represents the normalized propagation distance. T means the retarded time. \(\vartheta _2\) denotes the group velocity dispersion (GVD). \(\gamma\) indicates the Kerr nonlinearity. \(\vartheta _3(Z)\) represents the third-order dispersion (TOD). \(\tau (Z)\) describes the time delay related to the cubic term. \(\psi\) represents the external potential [16, 17]. Eq. (1) is the integrable form for the NLS equation and it can be utilized to describe the soliton interactions in inhomogeneous optical fibers (dispersion-flattened fibers). This kind of optical fiber makes long-distance transmission possible without the use of repeaters, and could potentially double transmission capacity as well [18]. Here, we discuss the effect of the TOD coefficient \(\vartheta _3(Z)\) on the structure of the soliton interactions. By choosing different values for \(\vartheta _3(Z)\) and the free parameters in the obtained solutions of Eq. (1), we will investigate the bound state of the soliton interactions which have potential applications in the formation of mode-locked fiber lasers and increase the transmission line bandwidth of optical communication systems. Liu et al. [19] derived the analytic three-soliton solutions for Eq. (1). However, we observe that exact solutions have not been studied much via the \(G'/G\)-expansion method and symbolic computation [20,21,22,23,24,25,26,27,28], which will become the main work of our paper. These analytical methods will be developed to deal with many of nonlinear complex partial differential equations with variable coefficients (Vc-NCPDEs). It is hoped that the obtained solutions can be used to enrich the dynamic behaviors for Vc-NCPDEs.

The organization of this paper is as follows. Section 2 presents the new exact solutions via the \((G'/G)\)-expansion method and symbolic computation, which contain dark soliton solutions. Section 3 gives the bright soliton solution, non-traveling wave solution, and periodic solution. Section 4 provides the similarity solutions. Section 5 gives the physical interpretation for some of the obtained solutions. The conclusion is investigated in Sect. 6.

2 Exact solutions

To seek the exact solutions of Eq. (1), we suppose

$$\begin{aligned} \Xi [Z,T]=e^{i \zeta (Z,T)} \Omega [\varrho (Z,T)], \end{aligned}$$
(2)

where \(\varrho =\Theta _1 T+\delta _1(Z)\) and \(\zeta =\Theta _2 T+\delta _2(Z)\) are real functions. \(\Theta _1\) and \(\Theta _2\) are unknown constants. \(\delta _1(Z)\) and \(\delta _2(Z)\) are unknown functions. Substituting Eq. (2) into Eq. (1) and separating the real and imaginary parts, we have

$$\begin{aligned}&\Omega (\varrho ) \{\psi +\Theta _2^2 [\vartheta _2+\Theta _2 \vartheta _3(Z)]- \delta _2'(Z)\}\nonumber \\&\quad -\Theta _1^2 [\vartheta _2+3 \Theta _2 \vartheta _3(Z)] \Omega ''(\varrho )\nonumber \\&\quad +[\gamma -\Theta _2 \tau (Z)] \Omega (\varrho )^3=0, \end{aligned}$$
(3)

and

$$\begin{aligned}&\Omega '(\varrho ) \{\Theta _1 [\tau (Z) \Omega (\varrho )^2-3 \Theta _2^2 \vartheta _3(Z)- 2 \Theta _2 \vartheta _2]\nonumber \\&\quad +\delta _1'(Z)\}+\Theta _1^3 \vartheta _3(Z) \Omega ^{(3)}(\varrho )=0. \end{aligned}$$
(4)

Integrating Eq. (4) with respect to \(\varrho\) once and by letting the integral constant to be zero, we get

$$\begin{aligned}&\frac{1}{3} \Omega (\varrho ) \{\Theta _1 [\tau (Z) \Omega (\varrho )^2-9 \Theta _2^2 \vartheta _3(Z)-6 \Theta _2 \vartheta _2]\nonumber \\&\quad +3 \delta _1'(Z)\}+\Theta _1^3 \vartheta _3(Z) \Omega ''(\varrho )=0. \end{aligned}$$
(5)

Let the coefficients of Eqs. (3) and (5) satisfy the following proportional relation

$$\begin{aligned} \frac{3 [\gamma -\Theta _2 \tau (Z)]}{\Theta _1 \tau (Z)}= & {} -\frac{3 \Theta _2 \vartheta _3(Z)+\vartheta _2}{\Theta _1 \vartheta _3(Z)} \nonumber \\= & {} \frac{\psi -\delta _2'(Z)+\Theta _2^2 [\Theta _2 \vartheta _3(Z)+\vartheta _2]}{\delta _1'(Z)-\Theta _1 \Theta _2 [3 \Theta _2 \vartheta _3(Z)+2 \vartheta _2]}. \end{aligned}$$
(6)

From Eq. (6), we have the constraints

$$\begin{aligned} \tau (Z)= & {} -\frac{3 \gamma \vartheta _3(Z)}{\vartheta _2},\nonumber \\ \delta _2(Z)= & {} \int \frac{\delta _1'(Z) [3 \Theta _2 \vartheta _3(Z)+\vartheta _2]+\Theta _1 [\psi \vartheta _3(Z)-2 \Theta _2 [2 \Theta _2 \vartheta _3(Z)+\vartheta _2]{}^2]}{\Theta _1 \vartheta _3(Z)} \, dZ+\phi _1, \end{aligned}$$
(7)

where \(\phi _1\) is integral constant. Substituting Eq. (7) into Eq. (3) (or Eq. 5), we have

$$\begin{aligned}&\Omega (\varrho ) [\Theta _1 [\vartheta _3(Z) [\gamma \Omega (\varrho )^2+3 \Theta _2^2 \vartheta _2]+2 \Theta _2 \vartheta _2^2]-\vartheta _2 \delta _1'(Z)]\nonumber \\&\quad -\Theta _1^3 \vartheta _2 \vartheta _3(Z) \Omega ''(\varrho ) =0. \end{aligned}$$
(8)

Based on the idea of the \((G'/G)\)-expansion method [29,30,31,32,33,34,35], the solutions of Eq. (8) can be supposed as

$$\begin{aligned} \Omega (\varrho )=a_{-1}(Z)\,\frac{G(\varrho )}{G'(\varrho )}+a_0(Z)+a_1(Z)\, \frac{G'(\varrho )}{G(\varrho )}, \end{aligned}$$
(9)

where G satisfies the auxiliary equation

$$\begin{aligned} G''(\varrho )+\lambda \,G'(\varrho )+\mu \,G(\varrho )=0. \end{aligned}$$
(10)

The solutions of Eq.(10) are given as

$$\begin{aligned} \frac{G'(\varrho )}{G(\varrho )}=\left\{ \begin{array}{ll} -\dfrac{\lambda }{2}+\tau _1 \dfrac{C_1 \cosh [\tau _1 \varrho ]+C_2 \sinh [\tau _1 \varrho ]}{C_1 \sinh [\tau _1 \varrho ]+C_2 \cosh [\tau _1 \varrho ]}, \lambda ^2-4 \mu >0, \tau _1 =\dfrac{\sqrt{\lambda ^2-4 \mu } }{2}, \\ -\dfrac{\lambda }{2}+\tau _2 \dfrac{-C_1 \sin [\tau _2 \varrho ]+C_2 \cos [\tau _2 \varrho ]}{C_1 \cos [\tau _2 \varrho ]+C_2 \sin [\tau _2 \varrho ]}, \lambda ^2-4 \mu <0, \tau _2=\dfrac{\sqrt{4 \mu -\lambda ^2 } }{2}. \end{array}\right. \end{aligned}$$
(11)

Substituting Eq. (9) along with Eq. (10) into Eq. (8) and equating all the coefficients of different powers of \([\frac{G'(\varrho )}{G(\varrho )}]^i (i=-3, \cdots , 3)\) to zero, we have

Case I

$$\begin{aligned} a_{-1}(Z)= & {} 0, a_1(Z)=\frac{\sqrt{2} \Theta _1 \epsilon _1 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, a_0(Z) = \frac{\Theta _1 \lambda \sqrt{\vartheta _2}}{\sqrt{2} \sqrt{\gamma } \epsilon _1},\nonumber \\ \delta _1(Z)= & {} \frac{1}{2} \Theta _1 \int [\vartheta _3(Z) [\Theta _1^2 \left( \lambda ^2-4 \mu \right) \nonumber \\&+6 \Theta _2^2]+4 \Theta _2 \vartheta _2] \, dZ+\phi _2, \end{aligned}$$
(12)

where \(\phi _2\) is integral constant, \(\epsilon _1=\pm 1\).

Case II

$$\begin{aligned} a_1(Z)= & {} 0, a_{-1}(Z)=\frac{\sqrt{2} \Theta _1 \mu \epsilon _2 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, a_0(Z) = \frac{\Theta _1 \lambda \sqrt{\vartheta _2}}{\sqrt{2} \sqrt{\gamma } \epsilon _2},\nonumber \\ \delta _1(Z)= & {} \frac{1}{2} \Theta _1 \int [\vartheta _3(Z) [\Theta _1^2 \left( \lambda ^2-4 \mu \right) +6 \Theta _2^2]\nonumber \\&+4 \Theta _2 \vartheta _2] \, dZ+\phi _2, \end{aligned}$$
(13)

where \(\epsilon _2=\pm 1\).

Case III

$$\begin{aligned} a_1(Z)= & {} \frac{\sqrt{2} \Theta _1 \epsilon _3 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, a_{-1}(Z)=\frac{\sqrt{2} \Theta _1 \mu \epsilon _3 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, \nonumber \\ a_0(Z)= & {} \frac{\Theta _1 \lambda \sqrt{\vartheta _2}}{\sqrt{2} \sqrt{\gamma } \epsilon _3},\nonumber \\ \delta _1(Z)= & {} \frac{1}{2} \Theta _1 \int [\vartheta _3(Z) [\Theta _1^2 \left( \lambda ^2+8 \mu \right) +6 \Theta _2^2]\nonumber \\&+\,4 \Theta _2 \vartheta _2] \, dZ+\phi _2, \lambda =0, \end{aligned}$$
(14)

where \(\epsilon _3=\pm 1\).

Case IV

$$\begin{aligned} a_1(Z)= & {} \frac{\sqrt{2} \Theta _1 \epsilon _3 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, a_{-1}(Z)=\frac{\sqrt{2} \Theta _1 \mu \epsilon _3 \sqrt{\vartheta _2}}{\sqrt{\gamma }}, \nonumber \\ a_0(Z)= & {} \frac{\Theta _1 \lambda \sqrt{\vartheta _2}}{\sqrt{2} \sqrt{\gamma } \epsilon _3}, \nonumber \\ \delta _1(Z)= & {} -\frac{\beta _2 \Theta _1^3 Z \left( \lambda ^2+8 \mu \right) }{6 \Theta _2}-\Theta _2 \Theta _1 Z \left( \beta _2-2 \vartheta _2\right) \nonumber \\&+\phi _2, \vartheta _3(Z)=-\frac{\beta _2}{3 \Theta _2}, \end{aligned}$$
(15)

where \(\epsilon _3=\pm 1\). By substituting Eq. (9) and Eq. (11) with the constraints (12), (13), (14), (15) into Eq. (2), respectively, an abundance of exact solutions for Eq. (1) can be obtained.

To show the properties and features of the obtained solutions, by substituting Eqs. (9), (11) and (12) into (2), we have

$$\begin{aligned} \Xi _1= & {} \left[ \Theta _1 \sqrt{\vartheta _2} \sqrt{\lambda ^2-4 \mu } \left[ C_1 \coth \left[ \frac{1}{4} \sqrt{\lambda ^2-4 \mu } \left[ \Theta _1 \left[ 2 T\right. \right. \right. \right. \right. \nonumber \\&+\int \vartheta _3 \left[ \Theta _1^2 \left( \lambda ^2-4 \mu \right) +6 \Theta _2^2\right] \nonumber \\&+\left. \left. \left. \left. 4 \Theta _2 \vartheta _2 \, dZ\right] +2 \phi _2\right] \right] +C_2\right] \exp \left[ \frac{1}{2} i \left[ 2 \left( \Theta _2 T+\phi _1\right) \right. \right. \nonumber \\&+\int 2 \psi +\Theta _2 \vartheta _3 [3 \Theta _1^2 \left( \lambda ^2-4 \mu \right) \nonumber \\&+2 \Theta _2^2]+\vartheta _2 [\Theta _1^2 \left( \lambda ^2-4 \mu \right) \nonumber \\&\left. \left. \left. +2 \Theta _2^2] \, dZ\right] \right] \right] \big / \left[ \sqrt{2} \sqrt{\gamma } \epsilon _1 \left[ C_2 \coth \left[ \frac{1}{4} \sqrt{\lambda ^2-4 \mu } \left[ \Theta _1 [2 T\right. \right. \right. \right. \nonumber \\&+\int \vartheta _3(Z) \left[ \Theta _1^2 \left( \lambda ^2-4 \mu \right) \right. \nonumber \\&+\left. \left. \left. \left. \left. 6 \Theta _2^2\right] +4 \Theta _2 \vartheta _2 \, dZ]+2 \phi _2\right] \right] +C_1\right] \right] , \end{aligned}$$
(16)
Fig. 1
figure 1

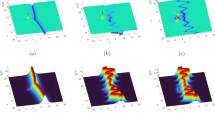
The absolute value for solution (16) with \(\lambda =-1, \mu =\phi _2=C_1=0, \vartheta _2=\Theta _2=C_2=\epsilon _1=1\), \(\gamma =2,\,\Theta _1=-3\), when \(\vartheta _3(Z)= -1\) a 3D plot. b Contour plot

Full size image
Fig. 2
figure 2

The absolute value for solution (16) with \(\lambda =-1,\,\mu =\phi _2=0, \vartheta _2=\Theta _2=C_2=\epsilon _1=1\), \(\gamma =C_1=2,\,\Theta _1=-3\) when \(\vartheta _3(Z)= -Z\) a 3D plot. b Contour plot

Full size image
Fig. 3
figure 3

The absolute value for solution (16) with \(\lambda =-1,\,\mu =\phi _2=0,\, \vartheta _2=\Theta _2=C_2=\epsilon _1=1\), \(\gamma =C_1=2,\,\Theta _1=-3\) when \(\vartheta _3(Z)= \cos Z\) a 3D plot. b Contour plot

Full size image

or

$$\begin{aligned} \Xi _2= & {} \left[ \Theta _1 \sqrt{\vartheta _2} \sqrt{4 \mu -\lambda ^2} \left[ C_2 \cot \left[ \frac{1}{4} \sqrt{4 \mu -\lambda ^2} \left[ \Theta _1 \left[ 2 T\right. \right. \right. \right. \right. \nonumber \\&+\,\int \vartheta _3 \left[ \Theta _1^2 \left( \lambda ^2-4 \mu \right) +6 \Theta _2^2\right] \nonumber \\&\left. \left. \left. +\,4 \Theta _2 \vartheta _2 \, dZ\left. \right] +2 \phi _2\right] \right] -C_1\right] \nonumber \\&\quad \exp \left[ \frac{1}{2} i [2 \left( \Theta _2 T+\phi _1\right) +\int 2 \psi \right. \nonumber \\&+\,\Theta _2 \vartheta _3 [3 \Theta _1^2 \left( \lambda ^2-4 \mu \right) \nonumber \\&+2 \Theta _2^2]+\vartheta _2 [\Theta _1^2 \left( \lambda ^2-4 \mu \right) \nonumber \\&\left. \left. +\,2 \Theta _2^2] \, dZ]\right] \right] /[\sqrt{2} \sqrt{\gamma } \epsilon _1 \left[ C_1 \cot \left[ \frac{1}{4} \sqrt{4 \mu -\lambda ^2} [\Theta _1 [2 T\right. \right. \nonumber \\&+\int \vartheta _3(Z) [\Theta _1^2 \left( \lambda ^2-4 \mu \right) +6 \Theta _2^2]\nonumber \\&\left. \left. +\,4 \Theta _2 \vartheta _2 \, dZ]+2 \phi _2]]+C_2\right] \right] . \end{aligned}$$
(17)
Fig. 4
figure 4

The absolute value for solution (17) with \(\lambda =\phi _2=0, \mu =\vartheta _2=\Theta _2=C_2=\epsilon _1=1 ,\,\gamma =2\), \(\Theta _1=-3\) when \(\vartheta _3(Z)= -1\) in a, d; \(\vartheta _3(Z)= - Z\) in b, e and \(\vartheta _3(Z)= \cos Z\) in c, f

Full size image

When \(\vartheta _3(Z)= -1\), the dynamical behaviors of solution (16) are demonstrated in Fig. 1. Figure 1 describes the propagation of dark soliton solution. When \(\vartheta _3(Z)=- Z\), the dynamical behaviors of solution (16) are shown in Fig. 2. Figure 2 describes the propagation of non-traveling wave solution. When \(\vartheta _3(Z)=\cos Z\), the dynamical behaviors of solution (16) are displayed in Fig. 3. Figure 3 shows the propagation of periodic solution. The dynamical behaviors of solution (17) are shown in Fig. 4 with \(\vartheta _3(Z)= -1\), \(\vartheta _3(Z)= -Z\) and \(\vartheta _3(Z)= \cos Z\), respectively.

3 Bright soliton solutions

This section is devoted to finding the bright soliton solutions.

To this end, we assume that

$$\begin{aligned} \Omega (\varrho )=\kappa _1 \text {sech}(\varrho ). \end{aligned}$$
(18)

Substituting Eq. (18) into Eq. (8), we obtain

$$\begin{aligned} \kappa _1= & {} \sqrt{2} \Theta _1 \epsilon _4 \sqrt{-\frac{\vartheta _2}{\gamma }},\nonumber \\ \delta _1(Z)= & {} \phi _2-\Theta _1 \int \left( \Theta _1^2-3 \Theta _2^2\right) \vartheta _3(Z)-2 \Theta _2 \vartheta _2 \, dZ, \end{aligned}$$
(19)

where \(\epsilon _4=\pm 1\). Substituting Eqs. (7), (18) and (19) into (2), the bright soliton solutions for Eq. (1) are written as

$$\begin{aligned} \Xi _3= & {} \sqrt{2} \Theta _1 \epsilon _4 \sqrt{-\frac{\vartheta _2}{\gamma }} \exp [i [\Theta _2 T+\int \psi +\Theta _2 \left( \Theta _2^2-3 \Theta _1^2\right) \vartheta _3(Z)\nonumber \\&+\left( \Theta _2^2-\Theta _1^2\right) \vartheta _2 \, dZ\nonumber \\&+\phi _1]] \text {sech}[\Theta _1 [T-\int \left( \Theta _1^2-3 \Theta _2^2\right) \vartheta _3(Z)-2 \Theta _2 \vartheta _2 \, dZ]+\phi _2]. \end{aligned}$$
(20)

The dynamical behaviors for bright soliton solutions (20) with the different values of \(\vartheta _3(Z)\) are described via Fig. 5.

Fig. 5
figure 5

The absolute value for solution (20) with \(\vartheta _2=-1,\, \Theta _2=\gamma =\epsilon _4=1,\, \phi _2=0,\,\Theta _1=2\) when \(\vartheta _3(Z)= -1\) in a, d, \(\vartheta _3(Z)=1+ Z\) in b, e, and \(\vartheta _3(Z)= \cos Z\) in c, f

Full size image

4 Similarity solutions

In Eq. (8), by assuming that

$$\begin{aligned} \vartheta _3(Z)= & {} -\frac{2}{\gamma \Theta _1}, \Theta _1= \epsilon _ 5 \sqrt{\frac{\gamma }{2 \vartheta _ 2}}, \delta _1(Z)=\sqrt{2 \gamma \vartheta _2} \Theta _2 Z \epsilon _5\nonumber \\&-\frac{6 \Theta _2^2 Z}{\gamma }-\frac{\Lambda Z}{\vartheta _2}+\phi _2, \end{aligned}$$
(21)

where \(\epsilon _ 5=\pm 1\), Eq. (8) becomes

$$\begin{aligned} \Lambda \Omega (\varrho )+\Omega ''(\varrho )-2 \Omega (\varrho )^3=0. \end{aligned}$$
(22)

The elliptic functions solutions for Eq. (22) have been discussed in Ref. [36]. Substituting the elliptic functions solutions for Eqs. (22) into (2), the corresponding similarity solutions for Eq. (1) can be obtained.

5 Physical interpretation for soliton interactions

In this part, discussions and physical interpretation for some of the obtained solutions will be demonstrated.

Figures 1, 2, 3 show different types of backgrounds for the dark solitons solution given by Eq. (16) in T–Z plane. It can be seen that the propagation trajectories of the dark solitons projected onto T–Z plane are straight lines, a parabolic type, and a periodic type when \(\vartheta _3(Z)=-1\), \(\vartheta _3(Z)=-Z\), and \(\vartheta _3(Z)=\cos Z\), respectively. Figure 1 depicts a transmission of the dark soliton with the invariant amplitude (without any gain or loss) in inhomogeneous optical fiber. Due to the inhomogeneous coefficient \(\vartheta _3(Z)=-Z\) in Fig. 2, the dark soliton propagates along a parabolic-type trajectory on the surface of a monotonically decreasing background. While in Fig. 3, the background undergoes a periodic oscillation due to inhomogeneous coefficient \(\vartheta _3(Z)=\cos Z\). With the previous results, we may provide a possible way to control the propagation of the dark solitons in the inhomogeneous optical fibers regime by choosing suitable values for the inhomogeneous TOD and the free parameters in the obtained solutions. Figure 4 introduces the solitons solution given by Eq. (17), which is singular solution, in T–Z plane. It is clear that the intensity of this solution gets stronger and consequently it is not stable.

Figure 5 represents different types of backgrounds for the bright solitons solution given by Eq. (20) in T–Z plane. The same discussion as in Figs. 1, 2, 3 can be introduced for this solution.

6 Conclusion

In the current investigation, an attempt was adopted to study the Hirota equation with variable coefficients, which describes soliton interactions in inhomogeneous optical fibers. The \(G'/G\)-expansion method was successfully exerted to acquire a bunch of different wave solutions including exact solutions, bright and dark soliton solutions, and similarity solutions. We found interesting behaviors, depending on the values of the free variable coefficients in the obtained solutions which are shown in Figs. 1, 2, 3, 4, 5. The results of this work come with a lot of encouragement for further future discussion in different branches of science, especially in nonlinear optics.