1 Introduction

With the rapid development of network information technology, information security has become crucial. Therefore, data encryption technology has become a hot topic of recent research [1,2,3,4]. As a branch of data security, optical information security has been rapidly developed due to its high degree of parallelism, high processing speed, and large-capacity storage. Since the optical image encryption system of double random-phase encoding [5] (DRPE) was proposed by Réfrégier and Javidi in 1995, the field of optical information security has attracted more and more researchers’ attention [6,7,8,9]. Subsequently, some typical optical information processing methods were combined with DRPE to achieve optical image encryption such as the fractional Mellin transformation [10, 11], fractional Fourier transformation [12, 13], and Fresnel transformation [14]. However, due to the linearity of DRPE systems, they are vulnerable to chosen-plaintext attacks [15, 16].

Klyshko first proposed ghost imaging scheme in 1988, and its obvious physical characteristics attracted the attention of scholars. Since Gatti and Brambilla completed ghost imaging experiments using classical thermal sources in 2004, ghost imaging has been widely used in the field of information security [17, 18]. Bromberg et al. proposed the concept of computational ghost imaging using only a single bucket detector in 2009 [19]. However, traditional ghost imaging required a large number of measurements. In order to reduce measurement time, Katz applied compressive sensing to ghost imaging to improve measurement efficiency.

In the previous works, random speckle patterns were applied to encryption systems of ghost imaging. However, the non-orthogonality of random patterns required a large number of measurements for high-quality reconstruction of encrypted images, although compressive sensing can be used to improve imaging quality and reduce the number of measurements, the results are not satisfactory. Recently, it has been proved that the single-pixel imaging technique using the basic patterns [20, 21] can achieve perfect reconstruction. Since the basic patterns form a complete orthogonal set, the basis patterns illumination allows people to obtain the spatial information of the object images in the transformation domain and restore the object images by the corresponding inverse transformation. Theoretically, the images information can be reconstructed perfectly when is fully sampled.

In order to improve the encryption efficiency of a large number of images, many scholars have recently paid more and more attention to methods of multi-image encryption, such as wavelength multiplexing, position multiplexing, and spatial multiplexing. In 2016, Jingjing et al. [22] proposed an optical multi-image encryption scheme based on computational ghost imaging and position multiplexing, in which each original image is encrypted into an intensity vector using computational ghost imaging with different diffraction distances, and the final ciphertext is generated by superimposing all the intensity vectors together, but as the number of images increases, the computational complexity and time consumption increase significantly; in 2016, Shengmei et al. [23] proposed a ghost imaging scheme with fast Walsh–Hadamard transform, however, which is applied to multiple images encryption, the ability to resist crosstalk among multiple images will decrease; in 2018, Sheng et al. [24] proposed an optical image encryption scheme based on DRPE and compressive ghost imaging, in which the secret image is transformed into a binary image using the DRPE technique based on phase retrieval, and then encoded by a series of random amplitude patterns according to the ghost imaging principle. In this paper, we propose a multi-image encryption method based on ghost imaging of Hadamard basic patterns and spatial multiplexing, in which the Hadamard basic patterns are applied to ghost imaging to achieve perfect reconstruction of the images, and combined with spectrum cropping and sampling of Fourier transformation to achieve data compression. Firstly, the theoretical analysis and description of the method are given, and then the numerical simulations are carried out. Finally, the conclusions are drawn.

2 Theoretical analysis and description

2.1 Compressive sensing ghost imaging theory

In computational ghost imaging, a bucket detector with no spatial resolution is used to collect the intensity values after diffraction through an object. A beam of parallel light is intensity modulated by a spatial light modulator (SLM) and illuminates onto an object to be imaged. The bucket detector detects the total intensity of light after diffraction through the object. In the imaging process, the SLM performs N random modulations in the detection optical path, and each modulation produces a speckle field with an intensity distribution \(I_{i} (x,y)\). The bucket detector is placed at the last to record of the N total light intensity values \(D_{i}\) corresponding to each random modulation. Finally, \(I_{i} (x,y)\) and \(D_{i}\) perform correlating operation, which can be expressed as the following equation:

$$G(x,y) = \langle I_{i} (x,y)D_{i} \rangle - \langle I_{i} (x,y)\rangle \langle D_{i} \rangle \quad i = 1,2, \ldots ,N,$$
(1)

where \(\langle \bullet \rangle\) represents average operation; \(G(x,y)\) represents a reconstructed image.

In order to improve the reconstruction quality of ciphertext, compressive sensing algorithm can be used for decryption. The process is shown in Eq. (2). The compressive sensing theory states that if the image or signal is sparse, then under certain conditions on the observation operator, it can be recovered exactly from the compressive measurements (Fig. 1)

$$T_{\text{CS}} = \arg \hbox{min} \left\| {T(x,y)} \right\|_{{L_{1} }} \quad {\text{s}} . {\text{t}} .\;D_{i} \quad \int {I_{i} } (x,y)T(x,y){\text{d}}x{\text{d}}y.$$
(2)
Fig. 1
figure 1

Schematic diagram of compressive sensing ghost imaging

Full size image

2.2 Hadamard basis patterns

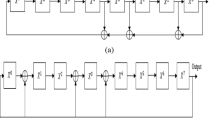
The Hadamard basis patterns which are standard orthonormal basis of binary (black and white) have horizontal and vertical characteristics. They are generated by a Hadamard matrix. Their elements consist of only + 1, − 1, and the rows (or columns) of the Hadamard matrix are reshaped into a two-dimensional square array to form the basis measurement patterns. The lowest-order Hadamard matrix is mathematically defined as

$$H_{2} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & { - 1} \\ \end{array} } \right].$$
(3)

Then, the following recursive formula is used to obtain a Hadamard matrix of order \(2^{k}\)

$$H_{{2^{k} }} = \left[ {\begin{array}{*{20}c} {H_{{2^{k - 1} }} } & {H_{{2^{k - 1} }} } \\ {H_{{2^{k - 1} }} } & { - H_{{2^{k - 1} }} } \\ \end{array} } \right].$$
(4)

The Hadamard basis pattern can be obtained by reforming the i-th row/column of the Hadamard matrix into a square pattern. Taking a 16-order Hadamard matrix as an example in Fig. 2, 16 Hadamard basis measurement patterns can be obtained by rearranging each row in \(H_{16}\) into a square pattern of \(4 \times 4\), which can perfectly reconstruct a \(4\times 4\) image.

Fig. 2
figure 2

a 16-order Hadamard matrix; b 16 Hadamard basis measurement patterns

Full size image

3 Multi-image encryption principle

In this paper, we use the Hadamard basis patterns that can completely recover images through inverse transformation in the case of complete sampling in principle, which solves the problem of low reconstruction quality in ghost imaging. At the same time, it allows people to reconstruct clear images with undersampling data, solving the problem of long acquisition time in ghost imaging.

3.1 Encryption process

The multi-image encryption method based on ghost imaging of Hadamard basis patterns and spatial multiplexing is shown in Fig. 3, and the encryption process is as follows:

Fig. 3
figure 3

Schematic diagram of multi-image encryption

Full size image

Step 1: Four original images with \(N \times N\) pixels are rearranged in descending order to reduce the natural frequency of the original image. An example of a descending operation performed is shown in Fig. 4.

Fig. 4
figure 4

Example of descending reordering operation

Full size image

Step 2: Fourier transform is applied to the rearranged images in step 1 to obtain spectral images; each spectral image is cropped into the image with \((N/k) \times (N/k)\) pixels, where k is the cropping coefficient.

Step 3: Inverse Fourier transform is applied to the spectral images with \((N/k) \times (N/k)\) pixels in step 2 .

Step 4: The restored images by inverse Fourier transformation in the step 3 \(f_{1} (x_{ 1} ,y_{ 1} ),f_{ 2} (x_{ 2} ,y_{ 2} ),f_{ 3} (x_{ 3} ,y_{ 3} ),f_{ 4} (x_{ 4} ,y_{ 4} )\) are combined into an image \(f(x,y)\) with \(N \times N\) pixels by spatial multiplexing technique when cropping coefficient k = 2, and the process is as follows:

$$f(x,y) = {\text{SUM}}\{ f_{1} (x_{1} ,y_{1} ),f_{2} (x_{2} ,y_{2} ),f_{3} (x_{3} ,y_{3} ),f_{4} (x_{4} ,y_{4} )\} .$$
(5)

Step 5: The combined image \(f(x,y)\) in the step 4 is encrypted by ghost imaging with Hadamard basis patterns, which are shown in Eq. (6). Therefore, the combined image can be reconstructed from the measurement result by the inverse Hadamard transformation, which is shown in Eq. (7).

$$g_{m} (u,v) = H\{ f(x,y)\} = \iint {f(x,y)P_{m} (x,y){\text{d}}x{\text{d}}y},$$
(6)
$$f(x,y) = H^{ - 1} \{ g_{m} (u,v)\} ,$$
(7)

where \((x,y)\) is the coordinate in the image space domain, \((u,v)\) is the coordinate in the Hadamard domain, \(H\{ \}\) represents two-dimensional Hadamard transformation, and \(H^{ - 1} \{ \}\) represents the inverse two-dimensional Hadamard transformation. \(P_{m} (x,y)(m = 1,2, \ldots ,N^{2} )\) represents \(N^{2}\) Hadamard basis patterns.

3.2 Decryption process

The multi-image decryption process based on ghost imaging of Hadamard basis patterns and spatial multiplexing is shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of multi-image decryption

Full size image

In the decryption process, the obtained ciphertext recovers the sorted image through measurement matrix formed by the Hadamard basis patterns, and then recovers the combined image with \(N \times N\) pixels through the correct position index matrix \({\text{SK}}_{i} \;(i = 1,2,3,4)\) of image pixels. Finally, it is divided into four images with \((N/k) \times (N/k)\) pixels, and they are enlarged, respectively, to the same size as the original images.

4 Simulation results and analysis

In order to verify the feasibility and robustness of the scheme, simulation experiments were carried out using MATLAB 2018a. The four original images with \(6 4\times 6 4\) pixels to be encrypted are shown in Fig. 6a–d, and the rearranged image in descending order is shown in Fig. 6e–h. The corresponding position index matrix of original images is shown in Fig. 6i–l, and Fig. 7a–d shows the images of the rearranged images after Fourier transformation. Then, Fig. 7a–d is cropped, and the reordered images are restored by inverse Fourier transformation. The four images are combined into one image by spatial multiplexing, which is shown in Fig. 7e. In the encryption system, the combined image is taken as an input image, and the result of the encryption is shown in Fig. 7f. Finally, the images recovered by decryption algorithm are shown in Fig. 7g–j.

Fig. 6
figure 6

a–d Original images; e–h corresponding images in descending order; i–l position index matrix of original images in descending order

Full size image
Fig. 7
figure 7

a–d Fourier spectrum of the rearranged images in descending order; e combined image by spatial multiplexing (recovered by IFFT after spectrum cropping); f ciphertext image; g–j reconstructed images

Full size image

4.1 Feasibility analysis

The feasibility analysis uses the optical information encryption method to evaluate the reconstructed plaintext information, and uses subjective judgment and objective parameters to measure the feasibility of algorithm. Here, we compare and analyze the encryption method proposed in this paper with the encryption method of original images without reordering. In the case of the spectrum cropping coefficient k = 2, Figs. 8 and 9, respectively, show the reconstruction effects of the two methods at different sampling rates.

Fig. 8
figure 8

Reconstructed images of the encryption method in this paper at different sampling rates

Full size image
Fig. 9
figure 9

Reconstructed images without descending ordering

Full size image

In order to objectively and accurately measure the quality of the image restored by the encryption method, it is measured by structural similarity (SSIM), which is an objective quality criterion for image quality in accordance with the characteristics of the human visual system. The higher the degree of similarity between the image to be evaluated and the original image, the larger the value, and the maximum is l. SSIM contains the luminance, contrast, and structural properties of the evaluation image, and its expression is

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {l(x,y) = \frac{{2\mu_{x} \mu_{y} + C_{1} }}{{\mu_{x}^{2} + \mu_{y}^{2} + C_{1} }}} \\ \end{array} } \\ {c(x,y) = \frac{{2\sigma_{x} \sigma_{y} + C_{2} }}{{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2} }}} \\ {s(x,y) = \frac{{\sigma_{xy} + C_{3} }}{{\sigma_{x} \sigma_{y} + C_{3} }}} \\ \end{array} } \right.,$$
(8)

where \(\mu_{x} ,\mu_{y}\) represent, respectively, the mean of the images x and y; \(\sigma_{x} ,\sigma_{y}\) represent, respectively, the standard deviation of the images x and y; \(\sigma_{xy}\) denotes the covariance of x and y; \(C_{1} ,C_{2} ,C_{3}\) are small constants, in order to avoid the occurrence of zero in the denominator to maintain stability. Taking into account all the above factors, the formula for calculating SSIM is shown in (11). In the formula, \(\alpha ,\beta ,\gamma\) are the three weights of three evaluation factors.

$${\text{SSIM}}(x,y) = \left[ {l(x,y)} \right]^{\alpha } \cdot \left[ {c(x,y)} \right]^{\beta } \cdot \left[ {s(x,y)} \right]^{\gamma } .$$
(9)

The larger the SSIM value, the better the image reconstruction quality and the visual effect. The SSIM values of the two methods at different sampling rates are shown in Fig. 10.

Fig. 10
figure 10

SSIM curves for the two methods at different sampling rates

Full size image

The red and black curves in Fig. 10 represent the case of reconstructing the original images of the method in this paper and the encryption method without reordering at different sampling rates. The six large dots represent six different reconstructed images at respective compression ratios. It is shown in Fig. 10 that (1) as the sampling rate increases, the SSIM value increases, that is, the larger the number of samples, the larger the SSIM value, the higher the quality of the reconstructed images, and the closer to the original images information; (2) when the sampling rate reaches about 40%, the image reconstructed by the method in this paper is close to the original image, however, the image reconstructed by the non-reordered encryption method has low definition. It explains that the images reconstructed by the scheme have better quality, which proves that the scheme is more effective in terms of feasibility.

4.2 Analysis of multi-image encryption capability

According to the characteristics of spatial multiplexing, if we use a larger cropping coefficient k, the smaller the center spectrum of cropping will be, the more images will be encrypted. Table 1 lists the reconstructed images at the crop coefficient \(k = 2,3,4\). It can be seen that as the cropping coefficient k increases, the quality of the reconstructed images decrease. Even if k = 4, the reconstructed images can be clearly recognized. Therefore, our proposed method can encrypt more than 16 images with \(6 4\times 6 4\) pixels.

Table 1 Reconstructed images at different cropping coefficients
Full size table

In order to objectively and accurately measure the quality of the reconstructed images under different cropping coefficients, an objective evaluation method is adopted here. Commonly used objective evaluation indicators are mean square error (MSE) and peak signal-to-noise ratio (PSNR). The basic idea is to measure the degree of deviation of the pixels of the reconstructed images and the original images, thereby evaluating the quality of the reconstructed images. For an image with M × N pixels, the mathematical expressions for MSE and PSNR are:

$${\text{MSE}} = \frac{{\sum\nolimits_{i = 1}^{M} {\sum\nolimits_{j = 1}^{N} {(O_{i,j} - O_{i,j}^{{\prime }} )^{2} } } }}{M \times N},$$
(10)
$${\text{PSNR}} = 10\lg \frac{{O_{\hbox{max} }^{2} }}{\text{MSE}},$$
(11)

where \(O_{i,j}\) and \(O_{i,j}^{{\prime }}\) represent, respectively, the values of the corresponding pixel points of the original image and the reconstructed image, and \(O_{\hbox{max} }\) represents the value of the largest pixel point in image. The larger the PSNR value, the more similar the two images are, that is, the higher the quality of reconstructed image, the better the capability of multi-image encryption in this paper. Figure 11 shows PSNR curves of decrypted images in which the number of encrypted images is 4, 9 and 16, respectively. (Take “house” as an example.)

Fig. 11
figure 11

PSNR curves of different numbers of encrypted images at different sampling rates

Full size image

It is shown in Fig. 11 that although the accuracy of reconstructed images will decrease as the number of encrypted images increases, the method can still achieve high-quality reconstruction, and with the increase in sampling rate, the distortion of reconstructed images is smaller and smaller, close to the original image, which indicates that the method is feasible in encrypting multi-image and more than 16 images can be encrypted.

4.3 Robustness analysis

4.3.1 Noise analysis

In the process of image encryption and transmission, noise attack is inevitable, which has non-negligible influence on the quality of the reconstructed image. Therefore, it is indispensable to evaluate the robustness of the encryption algorithm when the key or ciphertext is attacked by noise. Here, we choose Gaussian noise, salt and pepper noise, and Poisson noise to perform noise attack on the encrypted images, and test anti-noise ability of the proposed method. Figure 12a shows a ciphertext image after adding a Gaussian random noise with a mean of 0 and a variance of 0.03; Fig. 12b–e shows, respectively, decrypted images after adding Gaussian noise; Fig. 12f shows a ciphertext image after adding salt and pepper noise with a noise density of 0.03; Fig. 12g–j shows, respectively, decrypted images after adding salt and pepper noise; Fig. 12k shows the ciphertext image after adding Poisson noise; Fig. 12l–o shows, respectively, the decrypted images after adding the Poisson noise.

Fig. 12
figure 12

Reconstructed images under different noise attacks

Full size image

It is shown in Fig. 12 that the proposed method has good robustness to three kinds of noise attacks, and different noise attacks also have different reconstruction qualities for the decrypted images. Reconstructed images after Poisson noise attacks are better than images after Gaussian noise attacks and salt and pepper noise attacks. Although the quality of the decrypted images after the noise attack has decreased, the resolution of the reconstructed images is acceptable.

4.3.2 Cropping analysis

In the process of encryption transmission of images, loss of information is inevitable, which affects the quality of the decrypted images. Therefore, the anti-cropping performance of the encryption method is analyzed to verify the robustness of the proposed method. We cut the encrypted images in different sizes at different locations, and then use the correct key to decrypt the images. The reconstructed effect is shown in Fig. 13.

Fig. 13
figure 13

Reconstructed images with different positions and different sizes

Full size image

As shown in Fig. 13, the size of the cropping is different, and the reconstructed images will be different. As the cropping rate increases, the quality of the decrypted images will decrease. However, the images can still be distinguished, and the outline of the images can be seen. And the cropping at different positions, the resolution of the reconstructed image is not much different, indicating that the proposed method is robust to anti-cropping attacks. The resolution of the reconstructed images is not much different at different positions cropping, which indicates that the proposed method has good robustness to anti-cropping attack.

4.4 Security analysis

Security analysis is an important indicator to measure the performance of a encryption system. Here, we use the correlation coefficient in statistical analysis to verify the security of the method. Each pixel in the original image is not independent and has a strong correlation. One of the goals of image encryption is to reduce the correlation of the original image. The correlation coefficient measures the correlation of two adjacent variables in a certain direction mainly including the correlation of horizontal pixels, vertical pixels, and diagonal pixels. The closer the value approaches zero, the smaller the correlation between two adjacent values, which indicates that the better the image encryption effect and the higher the security. The correlation coefficient is calculated as follows:

$${\text{cc}} = \frac{{n\left( {\sum\nolimits_{i = 1}^{n} {u_{i} v_{i} } } \right) - \left( {\sum\nolimits_{i = 1}^{n} {u_{i} } } \right)\left( {\sum\nolimits_{i = 1}^{n} {v_{i} } } \right)}}{{\sqrt {\left[ {n\left( {\sum\nolimits_{i = 1}^{n} {u_{i}^{2} } } \right) - \left( {\sum\nolimits_{i = 1}^{n} {u_{i} } } \right)^{2} } \right]\left[ {n\left( {\sum\nolimits_{i = 1}^{n} {v_{i}^{2} } } \right) - \left( {\sum\nolimits_{i = 1}^{n} {v_{i} } } \right)^{2} } \right]} }},$$
(12)

where \([n(\sum\nolimits_{i = 1}^{n} {u_{i}^{2} } ) - (\sum\nolimits_{i = 1}^{n} {u_{i} } )^{2} ]\) and \([n(\sum\nolimits_{i = 1}^{n} {v_{i}^{2} } ) - (\sum\nolimits_{i = 1}^{n} {v_{i} } )^{2} ]\) represent, respectively, the standard deviation of the sample \(U_{j} ,V_{j} (j = 1,2, \ldots ,m)\), and \(U_{j} = \{ u_{j1} ,u_{j2} , \ldots ,u_{jn} \}\) represents a pixel vector of the image. The adjacent pixel vector of \(U_{j}\) is expressed as \(V_{k} = \{ v_{k1} ,v_{k2} , \ldots ,v_{kn} \}\), and k satisfies \(k = j + 1(j = 1,2, \ldots ,m - 1)\). The correlation coefficient of \(U_{j} ,V_{k}\) is obtained by formula (12), and the correlation coefficient of an image in a certain fixed direction can be obtained by calculating the average value. Some average correlation coefficients for the original images and the encrypted images are given in Table 2, and each correlation coefficient of the images in the horizontal and vertical directions is shown in Fig. 14.

Table 2 Average correlation coefficients of different images
Full size table
Fig. 14
figure 14

All correlation coefficients for different images

Full size image

Table 2 shows that the average correlation coefficients of different original images in the horizontal, vertical and diagonal directions are about 0.8, and the correlation is very strong. However, the correlation coefficients of the images after encryption in three directions are close to 0 at around 0.03, and the correlation is very weak, which indicates that the encryption scheme of this paper has good performance in terms of security.

The curve in Fig. 14 shows that the adjacent pixels of the original images have significant correlation, but the correlation is obviously weakened after encryption, and all correlation coefficients are evenly distributed in the range of 0–0.1, which shows that the encryption scheme of this paper has good effect and high security.

4.5 Compressibility analysis

In order to reduce the cost of storage and transmission, the signal is represented by a small number of bits with compressed mode, and a large amount of non-critical data is abandoned. In this paper, the multi-image encryption scheme uses the Fourier transformation and compressive sensing algorithm to achieve twice information compression. The compressibility is measured by the amount of transmitted information during the encryption process. For a \(N \times N\) image, the amount of transmitted information in ghost imaging is \(N^{2} /2\), and the amount of information in compressive sensing is \(M^{2} /2(M < N)\) when the number of sampling in compressive sensing is M. The amount of information compressed by the Fourier transformation is related to the number of encrypted images. We compare the three methods of ghost imaging, compressive ghost imaging, and the proposed method in this paper. Sampling rate of the four original images is 50%, and each image is compressed by 25% in the Fourier transformation compression. The amount of transmitted information is shown in Table 3.

Table 3 Amount of transmitted information under different encryption methods
Full size table

Table 3 shows that the amount of information transmitted by the scheme in this paper is 1024 bits, which greatly reduces the amount of transmitted information and reduces the storage space, and improves the transmission efficiency.

5 Conclusion

In this paper, a multi-image encryption method based on ghost imaging of Hadamard basis patterns and spatial multiplexing is proposed, which solves the problems of low imaging quality and long imaging time in traditional random illumination patterns. The encryption scheme concentrates most of the spectral information of the image on the lower frequency part by means of Fourier transformation, which uses central spectrum cropping to reduce the amount of information in the transmission process and achieves information compression. The Hadamard basis illumination patterns are used to reconstruct the original image perfectly in the case of full sampling. At the same time, the image with high quality can be reconstructed in the case of undersampling. The feasibility of the encryption scheme and the encryption capability of multiple images are verified by simulation experiments, and the scheme has also good robustness to the resistance of cropping and noise attacks.