1 Introduction

The diode-pumped alkali laser (DPAL) is a quasi-two level laser system using the lowest three energy states of the alkali vapor [1]. The gas is optically pumped on the \(D_2\) transition, \(n^2S_\frac{1}{2} \rightarrow n^2P_\frac{3}{2}\), then, in the presence of the buffer gas, is collisionally relaxed to the fine structure split \(n^2P_\frac{1}{2}\) state. When the population is inverted, the atom lases from there to the ground state in the near infrared [2]. The DPAL is a relatively new gas laser system for high-power applications [2, 3]. The DPAL system has been scaled to > 1  kW, with optical efficiency > 80%, and promises excellent beam quality [4]. Ideal, quasi-two level performance is achieved when the cycle rate is limited only by diode pump intensity. A pulsed potassium laser has been demonstrated with the time scale for fine structure mixing of 70 ps [5].

There are mechanisms that may populate higher lying levels, particularly for intensity scaled systems. If a significant alkali density is removed from the lower three levels, pump absorbance will be reduced, decreasing power efficiency. This effect may be largely mitigated by proper control of inlet or initial alkali density. Spatial variations in alkali density could lead to higher order uncorrectable effects. Furthermore, heat released from collisional deactivation of these higher lying states could adversely effect beam quality. There has been some controversy regarding the role of ionization in degrading efficiency at high pump intensity [6,7,8]. Experiments have shown that above 70 W of CW pump power, the output power falls off, dropping from 20 W with 70 W pump to 15 W at 100-W pump intensity [9]. Several theories have been posited to explain this phenomenon, including heating, alkali diffusion, and ionization.

Several previous models to describe ionization in DPALs have been developed [6, 10, 11]. For example a kinetic mechanism and fluid dynamics model to investigate static and flowing cesium DPAL, focused on the role of hydrocarbons in the lasing process [10]. Oliker et al. also produced a static model for a cesium DPAL that incorporates kinetic and fluid dynamics [11]. This three-dimensional model included thermal aberrations but neglects dissociative recombination. Knize suggests ionization rates may be catastrophically high in but does not fully evaluate restorative processes like recombination [6]. Full plasma models have also been developed. An analysis of a cesium DPAL suggested that laser power will experience major degradation, but less when a stronger quencher, nitrogen, is added as the buffer gas [7]. A second plasma model for a cesium excimer-pumped alkali laser (XPAL) concluded that with appropriate seed electrons the degree of ionization would be \(28.5\%\) [12]. This model accounted for 53 species of cesium, argon, and nitrogen in the cell. Despite these analyses, high-power devices have been developed with excellent efficiency [4, 7]

Processes that collisionally deactivate the higher lying levels may contribute to the total heat load and degrade device beam quality. The quantum defect in the potassium DPAL is particularly small (0.005), and the heat load for the ideal three level system is modest. Quenching of the diode pumped and upper laser levels by rare gases is sufficiency low to be difficult to measure. The larger energies associated with states near ionization might lead to substantially more heating, if the population of high-lying states is significant.

In this paper, a nine-level model is developed to describe the degree of ionization in a scaled potassium DPAL. The primary kinetic processes and their associated rate coefficients are reviewed and developed. Analytic steady-state solutions for the state populations are developed and used to assess the impact on laser efficiency. This work extends the prior analytic three-level model [1, 13] and forms the basis for analyzing new high-power, flowing potassium DPAL experiments.

2 Kinetic processes and rates

2.1 Energy levels

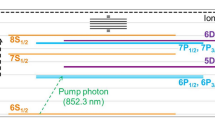
The energy level diagram for atomic potassium is provided in Fig. 1 and a summary of the key energy levels is provided in Table 1 [14]. The basic DPAL operates by diode pumping on the \(D_2\) transition, \(4\,^2S_{\frac{1}{2}}-4\,^2P_{\frac{3}{2}}\), collision induced transfer to the fine structure split \(4\,^2P_{\frac{1}{2}}\), followed by lasing back to the ground state. The fine structure splitting in K is modest, 57.71 cm\(^{-1}\), so that a statistical distribution at a temperature of 400 K yields a ratio for the population of the pumped and upper laser level of \(\frac{n_3}{n_2}=\frac{g_3}{g_2}\)exp\((-(E_3-E_2)/kT)=1.624\). The ionizational potential for potassium is 4.359 eV (35009.814 cm\(^{-1}\)), or 2.68 times the energy of the diode pumped, \(4\,^2P_{\frac{3}{2}}\) state, requiring 3 photons to ionize. The intermediate \(6\,^2S_{\frac{1}{2}},\, 5\,^2P_{\frac{3}{2},\frac{1}{2}}\), and \(4\,^2D_{\frac{5}{2},\frac{3}{2}}\) states lie near the energy associated with two pump photons, shown as a solid line in Fig. 1. The dashed line in Fig. 1 illustrates the lowest energy accessible to ionization via a single pump photon indicating that the \(5\,^2S_{\frac{1}{2}}\) and \(3\,^2D_{\frac{5}{2},\frac{3}{2}}\) are not involved in single-step photo-ionization, and are thus excluded from our designation as intermediate states. Levels lying above the intermediate states we group and designate the Rydberg states. We intend to track both atomic and dimer ions. The dissociation energy of \(K_2^+ (X)\) = 0.76 eV = 6130  cm\(^{-1}\) [15]. The DPAL alkali density is sufficiently low, \(\sim \, 10^{14}\) atoms cm\(^{-3}\) with melt pool temperatures of < 450 K, where the neutral dimer concentration in the absence of optical excitation is low < 1.5 % [16]. We neglect states with an orbital angular momentum quantum number \(L>2\, (^2F,^2G)\). We note that the fine structure splitting of the higher lying states is small, < 19  cm\(^{-1}\), and assume a statistical distribution between the J states, except for the pump and laser \(4\,^2P_{\frac{3}{2},\frac{1}{2}}\) states. The kinetic model will be reduced to predicting the population in nine levels of Table 1.

Fig. 1
figure 1

A energy diagram of potassium. The lowest three states form the standard DPAL system. The solid line at 21,996  cm\(^{-1}\) represents the energy of one pump photon above the 4P states. States above the dashed line can be ionized by a \(D_1\) or \(D_2\) photon

Full size image
Table 1 Relevant potassium energy levels and term symbols
Full size table

2.2 Three-level DPAL

The power peformance of various DPAL systems is usually well characterized by three-level kinetic models [17, 18]. The original model developed by Beach et al. [19] was extended to include longitudinal averaging [1] and broadband diodes [13]. More recent variants and extensions of this approach have been reported [5, 20,21,22]. The current study of multi-level kinetics begins with the baseline performance of this ideal three-level system.

Diode excitation from the ground \(4\,^2S_{\frac{1}{2}}\) state, with a population \(n_1\), to the pumped \(4\,^2P_{\frac{3}{2}}\) state, with population \(n_3\), proceeds via optical absorption on the \(D_2\) transition:

$$\begin{aligned} n_1+h\nu _p\rightarrow n_3, \end{aligned}$$
(1)

where h is Plank’s constant and the absorption cross-section at line center, \(\sigma _{13}\), is

$$\begin{aligned} \sigma _{13}=\frac{g_3}{g_1}\sigma _{31}=2\frac{\lambda _p^2}{8\pi }A_{31}g_{31}(\nu _0), \end{aligned}$$
(2)

where \(g_i\) is the degeneracy of the i-th state, \(\lambda _p\) is the pump wavelength, \(A_{31}\) is the spontaneous emission rate for the \(D_2\) transition, and \(g_{31}(\nu )\) is the spectral line shape. The core line shape is nearly Lorenztian at the DPAL elevated pressures and at line center,

$$\begin{aligned} g_{31}(\nu _0)=\frac{2}{\pi \varDelta \nu _L}. \end{aligned}$$
(3)

The Lorentzian width increases with pressure, \(\varDelta \nu _L=\sigma _b^{D2}uM\) where the broadening cross-section is weakly temperature dependent [23], u is the relative collision speed for the alkali-rare gas partner, and M is the rare gas concentration. At \(T=460\)  K and helium pressure \(P=760\) Torr, the \(D_2\) line width is 40.3 GHz.

Fine structure mixing is induced by a buffer gas, typically helium, with concentration M:

$$\begin{aligned} n_3+M\rightarrow n_2+M, \end{aligned}$$
(4)

and is rapid, \(k_{32}\) (400 K) = \(2.72\times 10^{-10}\)  cm\(^3\,\text {atom}^{-1} \text {s}^{-1}\) [24]. We use the most recently derived value for the spin-orbit cross-section, assuming independence of temperature. Alternatively, a temperature dependence may be derived from the many calculated values [24,25,26,27,28]. The inverse rate for fine structure mixing:

$$\begin{aligned} n_2+M\rightarrow n_3+M, \end{aligned}$$
(5)

is favored for potassium, with the bi-molecular rate coefficient constrained by detail balance:

$$\begin{aligned} k_{23}=k_{32}\frac{g_3}{g_2}\text {exp}[-(E_3-E_2)/kT]=k_{32}2 e^{-\theta }, \end{aligned}$$
(6)

where \(\theta =\frac{E_3-E_2}{kT}\) is associated with the spin-orbit splitting.

For a helium buffer gas pressure of 10 atmosphere at \(T=400\) K, the first-order mixing rate is \(\gamma _{32}=k_{32}M=4.99\times 10^{10}\)  s\(^{-1}\), or \(\kappa =\gamma _{32}/A_{31}=1309\) cycles per radiative lifetime. At higher pressures, the fine structure mixing rate can be enhanced by three body collisions. For a Rb–He mixture, three body collisions double the spin orbit rate at 3000 Torr [29]. However, the much faster two body rate in potassium will dominate the three body rate for realistic pressures, so it will be excluded from the mixing rate.

Relaxation back to the ground state can proceed via spontaneous emission at the pump or lasing frequency, \(\nu _{p,l}\):

$$\begin{aligned}&n_3\rightarrow n_1+h\nu _p, \end{aligned}$$
(7)
$$\begin{aligned}&n_2\rightarrow n_1+h\nu _l, \end{aligned}$$
(8)

with rates \(A_{31}=3.80\times 10^7\,\text {s}^{-1}\) and \(A_{21}=3.75\times 10^7\) s\(^{-1}\), or via quenching:

$$\begin{aligned}&n_3+M\rightarrow n_1+M, \end{aligned}$$
(9)
$$\begin{aligned}&n_2+M\rightarrow n_1+M. \end{aligned}$$
(10)

The quenching rates, \(k_{31}\) and \(k_{21}\), for collisions with pure helium are sufficiently low to usually be neglected [30]. We define the total decay rate from the two excited states as \(\gamma _3=A_{31}+k_{31}M\) and \(\gamma _2=A_{21}+k_{21}M\). Finally, the new lasing process terminates on the ground state:

$$\begin{aligned} n_2+h\nu _l\rightarrow n_1+2h\nu _l, \end{aligned}$$
(11)

where the stimulated emission cross-section at line center is:

$$\begin{aligned} \sigma _{21}=\sigma _{12}=\frac{\lambda ^2_l}{8\pi }A_{21}g_{21}(\nu _0). \end{aligned}$$
(12)

The K–He \(D_1\) line collision induced spectral broadening cross-section is \(\sigma ^{D1}_b=3.21\times 10^{-16}\, \text {cm}^2\) (13.1 MHz Torr\(^{-1}\)) at 328 K, 66\(\%\) of the \(D_2\) rate of \(\sigma ^{D2}_b=48.7\times 10^{-16}\, \text {cm}^2\) (19.8 MHz Torr\(^{-1}\)) [31, 32]. We suggest scaling the broadening rates with temperature assuming no temperature dependence for the collisional cross-section [33]:

$$\begin{aligned} \varDelta \nu _L=\gamma (T_1)P\left( \frac{T}{T_1}\right) ^{\frac{1}{2}}, \end{aligned}$$
(13)

where \(T_1\) is the temperature at which the cross-section is measured.

A comparison of the performance for the K, Rb, and Cs DPAL variants is provided in Table 2. The quantum efficiency is high \(\eta _{qe}=0.95-0.99\), with fine structure splitting relative to the kinetic energy, \(\theta =(E_3-E_2)/kT\), ranging from 0.181 to 1.739 at 460 K. The He mixing rate is rapid in potassium \(k_{32}(460\,K)=2.9\times 10^{-10}\, \text {cm}^3/(\text {atom}\,\text {s})\) [25], moderate for rubidium \(k_{32}(460\,K)=2.5\times 10^{-12}\, \text {cm}^3/(\text {atom}\,\text {s})\) [34], and too slow for cesium, \(k_{32}(460\,K)=9.5\times 10^{-15}\, \text {cm}^3/(\text {atom}\,\text {s})\) [34]. The Cs system requires the addition of a hydrocarbon to induce sufficient mixing. The temperature dependence of the spin-orbit cross-section in potassium may be included using a recent scaling law [35]. The buffer gas pressure necessary to achieve a mixing rate 20 times larger than the radiative rate, \(\kappa =k_{32}M/A_{31}\), increases for the heavier alkali vapors. Each atom cycles in the lasing process \(\kappa\) times per spontaneous event, a remarkable feature of the DPAL system. The helium pressure required to achieve this cycle rate increases from 125 Torr for potassium to 17,550 Torr for rubidium. Buffer gas pressures of 760 Torr require very aggressive diode bar spectral narrowing for efficient DPAL performance; 125 Torr would require narrowing not yet feasible at high pump powers. A helium pressure of \(5.08\times 10^6\) Torr would be required to achieve a \(\kappa =20\) for cesium. Therefore, in Table 2 760 Torr of helium is assumed for both potassium and cesium; whereas \(\kappa =20\) for cesium is achieved by introducing a modest amount of hydrocarbons. The melt temperature, \(T_\text {m}\), decreases for the heavier metal atoms and correspondingly the alkali density, N, at \(T=460\) K increases. The fractional population inversions, \(\varDelta /N\), have been evaluated using the longitudinally averaged pump intensity formalism by Hager et al. [1]. For the quasi-two level (Q2L) limit, where the fine structure mixing rate is infinite and the pump transition is nearly transparent, the steady state small signal (no lasing) inversion \(\varDelta _0^{Q2L}\), is a larger fraction of the total alkali density for the heavier atoms, where the fine structure splitting is larger. Indeed, for sodium and lithium, the system approaches two levels, the fractional inversion is low, and lasing has not been achieved. The fractional small signal inversion for the finite mixing rate associated with \(\kappa =20\) and a longitudinally averaged intracavity pump intensity, \(\varOmega =10\, \text {kW}\,\text {cm}^{-2}\), is most similar to the Q2L limit for the lighter alkali. The diode pump intensity required to achieve \(\varOmega =10\, \text {kW}\,\text {cm}^{-2}\), with a high absorbance \(A=\sigma _{21}nl=100\), increases from 14.0 kW \(\text {cm}^{-2}\) for K to 20.9 kW \(\text {cm}^{-2}\) for cesium. The relation between diode pump intensity, \(I_p\), and longitudinally averaged pump intensity, \(\varOmega\), is provided in Table 2, for lasing cavity of length \(l_g=10\) cm with nearly no loss (\(t=0.97\)), complete reflection of the pump diode at cell windows, and an output coupler reflectance of \(r=0.2\), corresponding to a gain threshold of \(g_{\text {th}}=0.086\, \text {cm}^{-1}\), by [1]:

$$\begin{aligned} \varOmega =\left( \frac{I_p}{\sigma _{31}(n_3-2n_1)l_g})(\exp [2\sigma _{31}(n_3-2n_1)l_g]-1\right) . \end{aligned}$$
(14)

Methods for calculation of the average intracavity lasing intensity, \(\varPsi\), and the output lasing intensity, \(I_l\), from the parameters described above is demonstrated by Hager et al. [1]. The optical–optical efficiency is generally high, \(\eta _{\text {oo}}=\frac{I_l}{I_p}=0.70-0.80\).

Table 2 Three-level DPAL performance characteristics at \(T=460\) K
Full size table

The output power of a DPAL system can be scaled by increasing diode pump intensity, or increasing the pumped area. Figure 2 provides the intensity scaling for the potassium system, assuming population is constrained to the three primary levels, using the longitudinally averaged approach [1, 13]. Threshold pump intensity is controlled by the requirement to bleach the full volume and scales linearly with alkali density. Scaling is linear with pump intensity until the system begins to bottleneck and is limited by the fine structure mixing rate. Increasing the cycle rate with a higher buffer gas pressure can increase this rate. The transition from the linear response to the bleached limit is rather abrupt for narrow band diodes, but somewhat shallower for broader spectral bandwidth.

Fig. 2
figure 2

Scaling of laser intensity with diode pump intensity in different regimes of Hager’s model [1, 13]. The solid blue line corresponds to the parameters in Table 2, the helium pressure is raised to 2 atm for the red dashed line (–), and the potassium density is doubled for the green dash–dot line (\(-\cdot\)). The small, black dotted line corresponds to a broadening of the pump source to 30 GHz and a pressure broadened Lorenztian absorption feature of the \(D_2\) transition. The red dots (\(\cdot\)) represent the heat loading of the original parameters in Table 2 with narrowband optical pumping

Full size image

The heat load for the three-level system, in a volume V, is dominated by energy release in the fine mixing rate, as the quenching of the \(n^2P_{\frac{3}{2},\frac{1}{2}}\) states is quite low [1]:

$$\begin{aligned} P_t=k_{32}M(n_3-2e^{-\theta }n_2)(E_3-E_2)V. \end{aligned}$$
(15)

For the conditions of Table 2, the potassium thermal power loading is, \(P_t=65.8\,\)W. This corresponds to a heating rate of \(\text {d}T/\text {d}t=7,731\, \text {K}\,\text {s}\), assuming no heat transfer. To keep the temperature rise modest, about 5 K, a longitudinal flow velocity of 146 m \(\text {s}^{-1}\), or a transverse flow speed of 14.6 m/s is required. Excitation of higher lying states will certainly increase the thermal effects and degrade beam quality or require higher gas flow rates. With the three-level baseline performance established, we now turn to assess the influence of the multi-level kinetics.

2.3 Intermediate states

The production of higher lying states will depopulate the three-level laser system, reducing the number of alkali atoms available to cycle, \(n_a\), by an amount \(\delta\), and thus reducing output power. Increasing the initial alkali density to compensate for this loss can largely mitigate this effect. The spatial distribution of alkali density due to localized heating could prevent a complete compensation. Furthermore, the heat load from quenching of these higher lying states may also degrade beam quality. To address these issues, we develop a multi-level kinetics model.

First consider the intermediate K \(6\,^2S_{\frac{1}{2}}\), \(5\,^2P_{\frac{3}{2},\frac{1}{2}}\) and \(4\,^2D_{\frac{5}{2},\frac{3}{2}}\) states near the energy associated with two pump photons, as shown in Fig. 1. The \(5\,^2S_{\frac{1}{2}}\) and \(3\,^2D_{\frac{5}{2},\frac{3}{2}}\) states lie below the energy required for single-step photo-ionization, and are thus excluded from the intermediate states. Several slow processes might contribute to the production of the intermediate states, including: (1) energy pooling, (2) far wing absorption of pump or laser radiation, and (3) two-photon absorption.

Energy pooling involves two excited atoms from the pumped or upper laser level states, \(n_i\) and \(n_j=2\) or 3 colliding to produce an intermediate \(n_f=4\)–6 and ground state atom:

$$\begin{aligned} n_{i}+n_{j}\rightarrow n_f+n_1. \end{aligned}$$
(16)

The final states, f, include both fine structure split levels. The pooling rates for excitation into each doubly excited (intermediate) state have been experimentally derived for most of the alkalies [36,37,38,39], and for many hetero-nuclear reactions [40]. The energy pooling cross-section for this reaction in Rb–K and Rb–Na has been modeled as a function of the energy difference for the pooled state and the sum of the energies of the two parent states [41]. We extend this scaling to the full set of observed alkali pooling reactions as shown in Fig. 3. The observed rates have been re-interpreted when needed to include both fine structure split product states in the cross-section. The experimental results were observed at temperatures ranging from 350 to 597 K [36, 38, 39, 41]. The cross-section, \(\sigma ^p\), is related to the rate coefficient, \(k^p\), via the average relative collision speed, u:

$$\begin{aligned} k^p_{i,j:f}=u\sigma ^p_{i,j:f}. \end{aligned}$$
(17)

While there is some scatter in the results, an exponential dependence on the absolute energy difference is well supported. Angular momentum considerations appear to be less significant. The scaling is asymmetric comparing results for excess and insufficient energy collisions, so two fits will be given. An un-weighted fit of the observations to the form:

$$\begin{aligned} \sigma ^p_{i,j:f}=\sigma _{o\pm }^p e^{a_{pm}\varDelta E/kT}, \end{aligned}$$
(18)

where \(\varDelta E=E_f-E_{i}-E_{j}\), yields \(a_+=-0.71\pm 0.28\) \(\sigma _{o+}^p=3.58\pm 1.8\times 10^{-14} \text {cm}^2\) and \(a_-=0.84\pm 0.04\) \(\sigma _{o+}^p=1.60\pm 0.58 \times 10^{-14} \text {cm}^2\). The fit values with the subscript \(+\) are used when \(\varDelta E>0\), and − when \(\varDelta E<0\). The rate coefficients for the most resonant cases are near gas kinetic, \(k^p\sim 10^{-10}\, \text {cm}^3/(\text {atom}\,\text {s})\), but the alkali density is low, \(N~\sim 10^{14}\, \text {atoms}\,\text {cm}^{-2}\), so the characteristic time scale is long \(\tau _p=1/k^pN\sim 0.1\, \text {ms}\). That rate corresponds to \(\sim 10^{-5}\) of the fine structure mixing rate and a minor influence on upper laser level population. However, the relaxation rates will be required to assess the steady-state concentrations.

The experimental results presented in Fig. 3 validates the need for a predictive tool, demonstrating significant scatter in individual results, an asymmetry about the origin and a lack of consistency in J dependence. The values plotted here are not J-state specific with regard to the final state, however, they are split for the two exciting states. Additionally, some rates, like \(4\,^2P\rightarrow 4\,^2D\) in potassium and \(5\,^2P\rightarrow 6\,^2P\) in rubidium, are missing from the literature. Thus, we use the scaled rates rather than specific experimental observations. The factor of 5 difference in the scaled and various experimental rates introduces less uncertainty than both the far wing absorption and quenching rates in the final prediction. Their rates were found to be between 4.00 and 7.07 \(\times 10^{-11}\,\text {cm}^3/(\text {atom}\,\text {s})\) at \(T=460\), and can be found as summarized in Table 5.

Fig. 3
figure 3

Pooling cross-section as a function of excess energy. The circled points represent the rates in potassium. A positive \(\varDelta E\) corresponds to an energy level below the pooled energy. The dashed line is fit similar to Gabbanini et al. [41], where it is suggested that the fit is better where \(\varDelta E>0\)

Full size image

Single-photon absorption from the pumped or upper laser level may also populate the intermediate states, but would be far from resonance [6]. For potassium, the \(D_2\) pump radiation would lie 1,131 \(\text {cm}^{-1}\) to the red of the nearest \(4\,^2P_{\frac{3}{2}}-4\,^2D_{\frac{3}{2}}\) resonance. At 760 Torr of helium, this would correspond to 446 Lorentzian widths from line center, assuming a broadening rate of 100 MHz Torr\(^{-1}\). Experimental values for the excited line shapes are not available. However, a better estimate for the broadening rates for the \(4\,^2P_{\frac{3}{2},\frac{1}{2}} \rightarrow 4\,^2D_{\frac{5}{2},\frac{3}{2}}\) and \(6\,^2S_{\frac{1}{2}}\) transitions might be provided by the quantum defect radii [35]. We use a helium radii of \(r_{\text {He}}=8.89\times 10^{-9}\) cm and the radii of the intermediate states from quantum defect theory:

$$\begin{aligned} n^*= & {} \sqrt{\frac{E_{\text {Ryd}}}{E_I-E}}, \end{aligned}$$
(19)
$$\begin{aligned} <r>= & {} a_0n^{*2}\left[ 1+\frac{1}{2}\left( 1-\frac{l(l+1)}{n^{*2}}\right) \right] . \end{aligned}$$
(20)

\(E_{\text {Ryd}}\) is the Rydberg constant, \(E_I-E\) is the energy gap between the excited state, E, and the ionization potential, \(E_I\). \(a_0\) the Bohr radius, and l is the orbital angular momentum quantum number. The predicted broadening cross-section is

$$\begin{aligned} \sigma _{QD}=\pi \left( r_{\text {He}}+<r>\right) ^2. \end{aligned}$$
(21)

The quantum defect broadening cross-sections for the P–D and P–S transitions are \(3.62\times 10^{-14}\, \text {cm}^2\) and \(4.84\times 10^{-14}\, \text {cm}^2\), respectively. These cross-sections corresponds to 134.4 and \(179.7 \text {MHz}\, \text {Torr}^{-1}\) at \(T=460\) K. We assume that the broadening is dominated by the upper (intermediate) state surface. Wing absorption to the \(5\,^2P_{\frac{3}{2},\frac{1}{2}}\) states is excluded, as the transitions are not electric dipole allowed.

High-pressure line shapes far from resonance are non-Lorentzian and can exhibit secondary maxima due to extrema in the interaction difference potentials. These far wing profiles are very sensitive to the interaction potentials [23, 42]. Unfortunately, the potentials for the higher lying state are available only at modest fidelity, not including any spin orbit effects [43]. The \(^2\varPi\) and \(^2\varSigma ^+\) potentials are calculated for the K–He complex for the 4P and 4D states, and the difference potentials of these are presented in Fig. 4. The top plots represent the two difference potentials with the \(^2\varSigma ^+\,4P\) state, and the bottom use the \(^2\varPi \,4P\). The attractive nature of the bottom difference potentials will lead to an enhancement on the red side of this transition, and the shallow minimum of the \(^2\varSigma ^+\,4D-^2\varPi ^+\,4P\) curve may lead to a satellite on the blue side. Robust potentials are required to better assess these non-Lorentzian effects.

Fig. 4
figure 4

Top: difference potentials between two upper states—\(^2\varSigma ^+\,4D\) (blue), \(^2\varPi \,4D\) (orange)—and the \(^2\varSigma ^+\,4P\) state. Bottom: difference potentials between two upper states—\(^2\varSigma ^+\,4D\) (blue), \(^2\varPi \,4D\) (orange)—and the \(^2\varPi \,4P\) state

Full size image

The quantum defect Lorentzian cross-section serves as a basis for evaluating the absorption into the wings. In Table 3, each of the intermediate states is coupled to both the pumped and upper laser levels by both pump and laser fields. While the excess energy for each of these transition is nearly the same, the cross-sections for have a much larger range.

Table 3 Absorption cross-section into the far wings for each transition at \(T=460\,K\) and \(P=760\) Torr
Full size table

The uncertainty in cross-sections and proximity of the \(D_1\) and \(D_2\) lines suggest simplification of the wing absorption rate from each state, \(R^w_i\), to a single term:

$$\begin{aligned} R^w_i=\frac{\alpha \sigma _L^i}{h\nu }(\varOmega +\varPsi )n^*, \end{aligned}$$
(22)

where the total population in the pumped and upper laser level is defined as \(n^*=n_2+n_3\). Recall, the intracavity pump intensity, \(\varOmega\) is given in Eq. (14) and the intracavity lasing intensity, \(\varPsi\), is developed for the three-level system in reference [1]. The wing absorption is separated into the Lorenztian cross-section, \(\sigma _L^i\), and an adjustable parameter, \(\alpha\), that accounts for the enhancement or degradation of the value due to non-Lorentzian behavior. In general, weighting the pump and lasing fields equally is likely inaccurate, with the rate due to the lasing field likely lower due to increased detuning from line center. Numeric estimates for the absorption cross-section 4P–5S transition near 1.2 \(\upmu m\) in potassium have demonstrated cross-sections in the far wings of the absorption profiles over two orders of magnitude larger than expected for Lorenztian detuning of 750 \(\text {cm}^{-1}\) [44]. Other simulations show that the far wings of the excitation cross-section of the 4S–4P can be increased over 1000 times larger than a Lorenztian broadened line [45]. The value of \(\alpha\) is a function of helium pressure [46], however, experimental results are required to determine this dependence. Further study of the far wing line shape for the excited–excited state transitions is clearly needed. We use \(\alpha =1\) for our baseline analysis.

Population of the intermediate states by pooling may dominate at higher alkali density, lower pump intensity and lower buffer gas density. Assuming a wing absorption cross-section of \(1.05 \times 10^{-19}\, \text {cm}^2\), commensurate to the \(4\,^2P\rightarrow 6\,^2S\) rate at 760 Torr, the K pooling and wing absorption rates are equal at \(n=1.50\times 10^{13}\, \text {atoms}\,\text {cm}^{-3}\) and \(\varOmega _p=13.4\, \text {kW}\,\text {cm}^{-2}\), or \(n=2.95\times 10^{14}\, \text {atoms}\,\text {cm}^{-3}\) and \(\varOmega _p=263\, \text {kW}\,\text {cm}^{-2}\). Wing absorption may dominate in most high-power DPAL systems.

Two-photon excitation from the ground state to the \(6\,^2S\) or \(4\,^2D\) states is significant when the pump radiation is tuned to the degenerate wavelength, 728.8 nm and 729.9 nm, respectively [47]. Indeed, these transitions can be bleached with pulsed lasers, and lasing has been observed after two-photon pumping with thresholds as low as \(260\, \text {kW}\,\text {cm}^{-2}\) [48]. The two-photon excitation cross-section is a function of the single-photon dipole moments and degree of detuning of the virtual states from the \(n^2P\) states [48]:

$$\begin{aligned} \sigma _{if}^{(2)}(\nu )=\frac{\pi ^2\nu }{5h^3c^2\epsilon _0^2} \sum \limits _n\frac{1}{g_ig_n} \frac{\mu ^2_{fn}\mu ^2_{ni}}{(\nu _{ni}-\nu )^2}g_f(\nu _{fi}=2\nu ). \end{aligned}$$
(23)

The sum introduced is over all atomic energy states, but only the states closest to the virtual state contribute substantially to the total. The subscript n denotes properties of these real intermediate states, \(\mu _{ni}\) is the dipole moment between the initial and intermediate states, \(\nu _{ni}\) is the frequency associated with that transition, and \(g_f(\nu _{fi}=2\nu )\) is the line shape for the single-photon transition from the initial to the final state. For example, the virtual state is detuned from the \(4\,^2P_{\frac{3}{2}}\) by 682.5 \(\text {cm}^{-1}\) for the K \(4\,^2S_{\frac{1}{2}}-6\,^2S_{\frac{1}{2}}\) two-photon transition and the peak cross-section is predicted \(\sim 1.2 10^{-25}\, \text {cm}^4\,\text {W}^{-1}\). For a diode pump at \(10\, \text {kW}\,\text {cm}^{-2}\) the corresponding rate is \(44.36\, \text {s}^{-1}\). However, at the pump and lasing wavelengths, the two-photon cross-section is highly detuned from resonance and the rates are negligible. Thus, we neglect the two-photon excitation.

Radiative decay from the intermediate and higher lying states occurs via cascading through several \(\varDelta L=\pm 1\) transitions. The spontaneous emission rates for K are summarized in Fig. 5 and Table 4 [14]. For example, the \(5\,^2P_{\frac{3}{2}}\) intermediate state radiates most rapidly to the \(5\,^2S_{\frac{1}{2}}\) state with a branching ratio of 0.63. Then the \(5\,^2S_{\frac{1}{2}}\) state radiates to the \(4\,^2P_{\frac{3}{2},\frac{1}{2}}\) states with a combined rate of \(2.35\times 10^{7}\, \text {s}^{-1}\). The cascade fluorescence complicates the processes and increases the the number of states that need to be monitored. This table also introduces a statistical fraction that corresponds to the percent of the population in each spin orbit split state:

$$\begin{aligned} f_i=\frac{g_i\exp {(E_i/kT)}}{\varSigma _j g_j \exp {(-\varDelta E/kT)}}, \end{aligned}$$
(24)

\(g_i\) is the degeneracy of the state and the sum is over all the split states. When calculating the total A-coefficient out of model state, each individual term is modulated by this fraction:

$$\begin{aligned} A=\varSigma _i f_i A_i. \end{aligned}$$
(25)

Quenching by buffer gas collisions also contributes to the relaxation, but these rates are less established. Quenching of higher lying S and D states in Na [49] and Rb [50, 51], moderate S and D states in Cs [52], and the \(10\,^2P\) state in K [53] have been observed. While quenching in the lowest P states is so slow as to be difficult to measure [54], inter-multiplet transfer strongly augments the rates for higher levels, with rates of \(3.3-210\times 10^{-11}\,\text {cm}^3/(\text {atom}\,\text {s})\). Quantum defect theory has been used to predict these rates and has been experimentally verified in lithium [55].

We choose to neglect the details of this relaxation and employ a single radiative and quenching term for each intermediate state. The recommended values are provided below in Table 5. The \(5\,^2P\) states require extra care as they can be populated by the other intermediate states, \(4\,^2D\) and \(6\,^2S\), via both spontaneous emission and quenching. The branching ratios of the emission rates from \(4\,^2D\) and \(6\,^2S\) to \(5\,^2P\) is in Table 4, but the proportion of quenching that terminates on \(5^2P\) is unclear. The products created by quenching of the intermediate states, in general, are important to the heat loading. The upper bound to the additional heat occurs if intermediates were quenched directly to the ground state. This, while unlikely, would lead to the least promising estimate of the beam quality. Quenching terminated on the nearest lower state is a more likely scenario. A third approach is to follow the branching ratios determined for the radiative rates as perturbation theory often leads to matrix elements that share the dipole moment. We chose this approach as an intermediate estimate between the other two extremes. Quenching from the Rydberg states are assumed to equally populate the three intermediates states, as the heat release is similar. The total quenching rate will be a model variable, and will require benchmarking. New experimental observations, and analysis of side fluorescence in a 1 kW flowing potassium DPAL system are in progress and will be particularly helpful in defining the quenching rates.

Production of the lowest three levels due to radiative and collisional relaxation from higher lying states is neglected, as the total population in the intermediate state is expected to be a small fraction of the total alkali density.

Fig. 5
figure 5

The Einstein A-coefficient for transitions in potassium as a function of the quantum number of the initiating state. Each trend is a different transition type; (green \(\bullet\)) \(S_{\frac{1}{2}}\rightarrow P_{\frac{3}{2},\frac{1}{2}}\), \(D\rightarrow P\) (dark blue \(\circ\): \(D_{\frac{3}{2}}\rightarrow P_{\frac{3}{2},\frac{1}{2}}\) and light blue \(\circ\): \(D_{\frac{5}{2}}\rightarrow P_{\frac{3}{2}}\)), and (black \(+\)) \(P_{\frac{3}{2},\frac{1}{2}}\rightarrow S_{\frac{1}{2}}\)

Full size image
Table 4 A-coefficient and branching of the intermediate states [14]
Full size table

Cascade lasing among these higher lying states has been observed, but only after two-photon excitation [48]. The energy pooling and wing absorption production rates appear too slow to invert these levels under cw excitation on the \(D_2\) line.

2.4 Ionization

All three intermediate states are within one pump photon from ionization; needing only 7,611, 10,289, and 7,558 \(\text {cm}^{-1}\) to ionize from \(n_4,\,n_5\) and \(n_6\), respectively, where a pump photon has 13,043 \(\text {cm}^{-1}\). Excitation of the intermediates states to produce ions may occur via direct photo-ionization, Penning ionization and Hornbeck–Molnar ionization. Photo-ionization may dominate for high pump intensities and moderate alkali densities. The three intermediates states, \(i=\)4,5, and 6, can be photo-ionized by either the pump or laser radiation:

$$\begin{aligned} n_i+h\nu \rightarrow n^++e^-, \end{aligned}$$
(26)

where \(n^+\) represents the concentration of the atomic ion and \(e^-\) represents the electron density.

These photo-ionization cross-sections, \(\sigma _i^{ph}\), have been computed as a function of the excess energy of the free electron for many lower S and D states [56]. For the potassium P states, only the pumped \(4\,^2P\) states have been reported, so the same trend was assumed for the higher P states [56]. The photoionization cross-sections for various excited states of potassium are provide in Fig. 6. The cross-section for the D states are highest and that of the S states are significantly lower. The photoionization cross-sections were also computed using quantum defect theory [57] and are included in the figure. As n increases, the photoionization cross-section decreases, but quantum defect theory does not capture this trend. While the cross-sections depend on wavelength, the rates for the pump \(D_2\) and lasing \(D_1\) fields are nearly identical.

Fig. 6
figure 6

The photoionization cross-sections for the \(nP (\star )\) and \(nD (\circ )\) in potassium are calculated from both the quantum defect theory (red) and numeric methods (black) [56]

Full size image

Penning ionization involves the collision or two excited alkali atoms and pools the energy to exceed the ionization potential:

$$\begin{aligned} n_{i}+n_{j}\rightarrow n^++e^-+n_1, \end{aligned}$$
(27)

where \(i=4,5,\) or 6 and j can be any excited state. However, the concentration of the pumped \(4\,^2P\) states is considerably larger than the intermediates, so the rate with the collision partner as \(n_2\) or \(n_3\) should dominate, and \(j=2\) or 3. The Penning ionization rates have not been measured in potassium. However, they were observed in rubidium for a wide range of energy levels, as shown in Fig. 7 [58]. The cross-sections, \(\sigma ^{\text {Pen}}\) are scaled here by the quantum defect cross-section, \(\sigma _{QD}\), to express a probability of Penning ionization. The effective quantum number is the most important factor in controlling this cross-section, with only small variations due to angular momentum. Even so, Penning cross-sections are relatively independent of n, but as \(\sigma _{QD}\) grows with \(n^*\), the probability decreases with more excess energy. This study did not distinguish between \(^2P_{\frac{3}{2}}\) and \(^2P_{\frac{3}{2}}\) collision partners, and only measured these rates out of S and D states [58]. The values predicted for potassium have been added to Fig. 7 along the exponential fit, \(\sigma ^{\text {Pen}}/\sigma _{QD}= (47.69\pm 25.12) \exp {((-0.67\pm 0.23) n^*)}\). The effective quantum number, \(n^*\) is very nearly equal for \(4\,^2D\) and \(6\,^2S\), so their points on the line are nearly overlapped. The predicted values in potassium are provided in Table 5.

Fig. 7
figure 7

Cross-section for Penning ionization for: (\(\bullet\)) Rb, (\(\circ\)) K, and (−) exponential fit to Rb calculations [58]

Full size image

A third mechanism to ionization occurs with the formation of the alkali dimer. This Hornbeck–Molnar ionization occurs when a collision between a ground state atom and an excited atom can create an ionic diatom and a free electron. The rate coefficient for this is nearly 100 times smaller than the rate coefficient for Penning ionization for all excited states of rubidium [58] and is excluded in the current model.

2.5 Ion recombination

The balance of the photo and Penning ionization production with recombination processes controls the ion concentration. The rates for radiative recombination are portioned into various atomic neutral states j:

$$\begin{aligned} n^++e^-\rightarrow n_j+h\nu , \end{aligned}$$
(28)

and are slow, \(k^{rr}<10^{-13}\, \text {cm}^3\,\text {atom}^{-1}\,\text {s}^{-1}\) [59], and excluded in the current model. The three-body recombination:

$$\begin{aligned} n^++e^-+M\rightarrow n_j+M, \end{aligned}$$
(29)

rate in Cs with helium as the collision partner is fast for such processes, \(k_{3B}=4\times 10^{-29}\, \text {cm}^6\,\text {s}^{-1}\) [60]. For a helium density of \(M=1.58\times 10^{19}\, \text {atoms}\,\text {cm}^{-3}\), 760 Torr at \(T=460\) K, the effective bi-molecular rate coefficient is \(k_{3B}M=5.9\times 10^{-10}\,\text {cm}^3\,\text {atom}^{-1}\,\text {s}^{-1}\), much faster than radiative recombination. We assume the dominant channel produces Rydberg states only, \(j=7\).

Dissociative recombination,

$$\begin{aligned} n^+_2+e^-\rightarrow n_j+n_1, \end{aligned}$$
(30)

involves the diatomic ion with density, \(n^+_2\), and likely yields high-lying neutral atomic states with \(j=7\), as discussed below. In cesium, this rate constant was calculated to be \(k_{DR}=5.26\times 10^{-7} \text {cm}^3\,\text {atom}^{-1}\,\text {s}^{-1}\) for \(T<1650\) K [61]. This rate coefficient is much larger than the three-body recombination rate and will dominate if the dimer ion concentration is significant. This rate was calculated at temperatures much higher than that of a typical DPAL, and the dependence of this rate on temperature is not well established. In a less plasma-like environment, this rate may be dramatically lower. However, it is the only value for this rate in the literature, so it is cautiously used in this model. Molecular ions are created during a three-body collision between a neutral alkali atom, alkali ion, and the buffer gas:

$$\begin{aligned} n+n^++M\rightarrow n^+_2+M. \end{aligned}$$
(31)

Experimental data suggest that the rate of reaction is 100 times larger when the third particle is another alkali. However, for DPAL conditions the rare gas density is much greater, \(> 10^6\) times larger, than the alkali density. The rate of reaction for the formation of the cesium ionic dimer in argon is very fast, \(k_{a}=2.4\times 10^{-23}\, \text {cm}^6\,\text {atom}^{-1}\,\text {s}^{-1}\) [62], and is the key pathway for recombination. The rate for Eq. (31) is much faster than Eq. (29), which supports the dimer being the dominant ion specie, and \(n_e\sim n_2^+\).

The density of electrons is not included in this model. It is possible that the electron temperature is much higher than the gas temperature. Free electrons can be excited collisionally or optically, coupling with the pump or lasing fields. Excited free electrons can then give this energy back to the alkali or put it into the buffer gas through quenching. The former will increase the population in the excited states, while the latter will increase the thermal energy and heat loading. If ionization only reaches \(1\%\) of the alkali density, the electron density will be \(\sim 1\times 10^{11}\, \text {cm}^{-3}\), which may be enough to observe the omitted adverse effects.

2.6 Rydberg states

The high-lying levels above the intermediates states are likely produced primarily by the dissociative recombination of Eq. (30). Curve crossings between repulsive neutral dimer states and ground state ion dimer molecules lead to the formation of excited potassium atoms during a collision with an electron. The dissociation energy of the ground molecular state of the ionic dimer, \(X^2\varSigma _g^+\), is \(D_0^0=0.76\) eV [15]. These states are probably quenched rapidly at higher buffer gas pressures and the radiative and collisional cascade to intermediate states follows the discussion associated with Fig. 5. We include theses states in the nine-level model to enable comparisons with visible and near infrared fluorescence spectra from flowing, high-power DPAL operation.

3 Rate equations

The rate equations for the nine-level model are now developed and form the basis for the performance model. We use the longitudinally averaged diode pump intensity, \(\varOmega\), and the intracavity laser intensity, \(\varPsi\), to characterize the optical rates, as previously developed for the three-level system [1]. The rate equations for the ground, \(n_1\), diode pumped, \(n_3\), and upper laser level, \(n_2\), are

$$\begin{aligned} \frac{\text {d}n_1}{\text {d}t}= & {} -\sigma _{13}\frac{\varOmega }{h\nu _p}\left( n_1-\frac{g_1}{g_3}n_3\right) +\sigma _{12}\frac{\varPsi }{h\nu _l}(n_2-n_1)+\gamma _2 n_2\nonumber \\&+\gamma _3 n_3, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\text {d}n_2}{\text {d}t}= & {} -\sigma _{12}\frac{\varPsi }{h\nu _l}(n_2-n_1)-\gamma _2 n_2+\gamma _{32} \left( n_3-n_2\frac{g_3}{g_2} e^{-\theta }\right) , \end{aligned}$$
(33)
$$\begin{aligned} \frac{\text {d}n_3}{\text {d}t}= & {} \sigma _{13}\frac{\varOmega }{h\nu _p}\left( n_1-\frac{g_1}{g_3}n_3\right) -\gamma _3 n_3-\gamma _{32} \left( n_3-n_2\frac{g_3}{g_2} e^{-\theta }\right) , \end{aligned}$$
(34)

where the degeneracy ratio, \(\frac{g_3}{g_1}=2\), the fine structure mixing rates are constrained by detailed balance as in Eq. (6), and the total decay rates include spontaneous emission and quenching, \(\gamma _3=A_{31}+k^q_{31}M\) and \(\gamma _2=A_{21}+k^q_{21}M\). Laser performance is affected only by the depletion of total alkali density in the three lowest levels. The three Eqs. (32), (33), and (34) are not linearly independent, and Eq. (32) can be eliminated in favor of the conservation statement:

$$\begin{aligned} n_1+n_2+n_3=N_a=N-\delta , \end{aligned}$$
(35)

where the total alkali density, N, has been reduced to the concentration available to the three level system, \(N_a\), by the concentration in the higher lying and ionized states:

$$\begin{aligned} \delta =(n_4+n_5+n_6)+n_7+n^++2n^+_2. \end{aligned}$$
(36)

Source terms from quenching and radiation of the intermediates states have been omitted from Eqs. (32), (33), and (34) and the results are limited to the modest multi-level excitation expected for DPAL conditions. We have also neglected the removal of population from the pumped and upper laser levels due to Penning ionization, pooling and wing absorption. That is, we are considering the perturbation to the three-level model to be small. Figure 8 demonstrates why we can make this assumption. In this, the rate of spontaneous emission from the \(4^2\,P_{\frac{3}{2}}\), \(n_3A_{31}\), shown in blue is nearly an order of magnitude larger than the energy pooling rate, discussed after Eq. (45), shown in orange, and the spontaneous emission rate from the intermediate states, discussed after Eq. (42), shown in yellow. Recall, the spin orbit rate, and, therefore, the lasing cycle, needs to be at least 20 times faster than the spontaneous emission rate to create an efficient laser.

Fig. 8
figure 8

Kinetic rates, shown as a function of alkali density, at 1 atm buffer gas and pump intensity of \(I_p=25\, \text {kW}\,\text {cm}^{-2}\). The blue line represents spontaneous emission out of \(4^2\,P_{\frac{3}{2}}\), the orange is the pooling rate out of the same state, and the yellow is the total spontaneous emissions from all of the intermediate states

Full size image

For very high pump intensities where the \(D_2\) transition is highly saturated, \(\varOmega>>I_{sat}=\frac{A_{31}h\nu _p}{\sigma _{31}}\), the first term in Eq. (34) demands a bleached population difference:

$$\begin{aligned} (n_1-n_3/2)_b=0. \end{aligned}$$
(37)

When this occurs, and in the absence of lasing \(\varPsi =0\), the Q2L, the small signal solution of Table 2 is completed by requiring the equilibrium of the pumped and upper laser level:

$$\begin{aligned} \gamma _{32}(2e^{-\theta }n_2-n_3)-\gamma _3 n_3=0. \end{aligned}$$
(38)

When the fine structure mixing rate is very large, \(\kappa =\gamma _{32}/A_{32}\rightarrow \infty\),

$$\begin{aligned} 2e^{-\theta }n_2=n_3, \end{aligned}$$
(39)

and Eq. (39) replaces the CW solution to Eq. (33). The limiting cases of Eqs. (38) and (39) are not assumed when computing the lower three laser levels or the lasing intensity, but allows for a significantly easier computation of the population in the higher lying levels with and without lasing. This approximation is within \(8\%\) of the true population after only 1 atm of buffer gas is added, and is off by \(<1\%\) with 10 atm of helium.

The population in the intermediate states are defined by the rate equations:

$$\begin{aligned} \frac{\text {d}n_4}{\text {d}t}=&(k_{2,2:4}^p n_2 n_2+k_{2,3:4}^pn_2n_3+k_{3,3:4}n_3n_3)\nonumber \\&+\frac{\sigma _L^4}{h\nu _p}(\varOmega +\varPsi )(n_2+n_3)\nonumber \\&-n_4\gamma _4-n_4k_{4}^{PI}(n_3+n_2)-n_4\frac{\sigma _4^{ph}}{h\nu _p}(\varOmega +\varPsi ), \end{aligned}$$
(40)
$$\begin{aligned} \frac{\text {d}n_5}{\text {d}t}=&(k_{2,2:5}^p n_2 n_2+k_{2,3:5}^pn_2n_3+k_{3,3:5}n_3n_3)\nonumber \\&-n_5\gamma _5-n_5k_{5}^{PI}(n_3+n_2)-n_5\frac{\sigma _5^{ph}}{h\nu _p}(\varOmega +\varPsi )\nonumber \\&+\gamma _{45}n_4+\gamma _{65}n_6, \end{aligned}$$
(41)
$$\begin{aligned} \frac{\text {d}n_6}{\text {d}t}=&(k_{2,2:6}^p n_2 n_2+k_{2,3:6}^pn_2n_3+k_{3,3:6}n_3n_3)\nonumber \\&+\frac{\sigma _L^6}{h\nu _p}(\varOmega +\varPsi )(n_2+n_3)\nonumber \\&-n_6\gamma _6-n_6k_{6}^{PI}(n_3+n_2)-n_6\frac{\sigma _6^{ph}}{h\nu _p}(\varOmega +\varPsi ), \end{aligned}$$
(42)

where \(\gamma _i=A_i+k_iM\) and represents the depopulation methods our of the excited states; \(A_i\) is the total Einstein A-coefficent and \(k_i\) is the total quenching rate out of excited state i. Each of these can be broken down further into final state specific rates: \(A_i=\varSigma _j A_{ij}\) and \(k_i=\varSigma _j k_{ij}\). The final two terms in Eq. (41) represent the emission and quenching terms between the intermediate states, \(\gamma _{45}=A_{45}+k^q_{45}M\) and \(\gamma _{65}=A_{65}+k^q_{65}M\). This depopulation out of \(4\,^2D\) and \(6\,^2S\) are accounted already for in \(\gamma _4\) and \(\gamma _6\).

Due to the small energy differences between the \(4\,^2D\) and \(6\,^2S\), \(\varDelta E\approx 50\, \text {cm}^{-1}\), we have assumed that the wing absorption rate to both states are equal. Additionally, we have assumed that the wing absorption rate due to the two fields are equal. Enhancement features in the far wings of the absorption line shape may be smaller than these splittings. However, these line shapes have not been experimentally derived or numerically calculated to the precision needed to assume a more precise value. For the sake of simplicity, we employ a common wing absorption cross-section. Future modification of the model to incorporate specific cross-sections is straightforward.

Equations (40)–(42) are simplified using the quasi-two level limit (39) to make \(n_2\) a function of \(n_3\), for example:

$$\begin{aligned} k^{p}_4= & {} k_{2,2:4}^{p}\frac{n_2^2}{n_3^2}+k_{2,3:4}^{p}\frac{n_2}{n_3} +k_{3,3:4}^{p}=k_{2,2:4}^p\frac{e^{2\theta }}{4} +k_{2,3:4}^{p}\frac{e^{\theta }}{2}\nonumber \\&+k_{3,3:4}^{p}. \end{aligned}$$
(43)

A similar technique can be used to consolidate the other Penning rates, as well as the energy pooling rate coefficients. Additionally, these three levels can be combined into a single kinetic level by summing Eqs. (40)–(42) using the grouping of:

$$\begin{aligned} n^{**}= & {} n_4+n_5+n_6 \end{aligned}$$
(44)
$$\begin{aligned} \frac{\text {d}n^{**}}{\text {d}t}= & {} K^p n_3^2+\frac{\sigma _w}{h\nu _p}(\varOmega +\varPsi )(n_2+n_3)\nonumber \\&-n^{**}n_3K^{PI}-n^{**} \frac{\sigma ^{ph}}{h\nu _p}(\varOmega +\varPsi )-n^{**}\gamma _{**}. \end{aligned}$$
(45)

An equal distribution for the three states is assumed, such that, \(K^p=k^p_4+k^p_5+k^p_6\), \(\sigma ^{ph}=\sigma ^{ph}_4+\sigma ^{ph}_5+\sigma ^{ph}_6\), and \(K^{PI}=k^{PI}_4+k^{PI}_5+k^{PI}_6\), and \(\sigma _w=\sigma _L^4+\sigma _L^6\). Validation of this assumption requires some experimental effort to investigate the true distribution amongst these states. The value \(\gamma _{**}=\gamma _4+\gamma _5+\gamma _6-\gamma _{45}-\gamma _{65}\) requires careful consideration, as transfer within this level does not effect the population, but will still be a source of heat loading.

The production of intermediates from decay of the Rydberg states or products of the ionic dimer recombination are minor paths excluded from Eqs. (40), (41) and (42). This approximation allows for the decoupling of the intermediate states from the higher lying levels and an equation of the total intermediate concentration directly from the populations in the three level system.

The rate equations are completed by evaluating the populations in the Rydberg (\(n_7\)) and ionized states:

$$\begin{aligned} \frac{\text {d}n_7}{\text {d}t}= & {} k_{DR}n_2^+(n_2^++n^+)-\gamma _7n_7, \end{aligned}$$
(46)
$$\begin{aligned} \frac{\text {d}n_2^+}{\text {d}t}= & {} k_aMn^+N-k_{DR}n_2^+(n_2^++n^+), \end{aligned}$$
(47)
$$\begin{aligned} \frac{\text {d}n^+}{\text {d}t}= & {} k^{PI}n_3n^{**}+\frac{\sigma ^{ph}}{h\nu _p}(\varOmega +\varPsi ) n^{**}-k_aMn^+N, \end{aligned}$$
(48)

where the electron density has been replaced by the sum of the atomic and dimer ion concentrations, as required by charge neutrality, and the association rate proceeds with all alkali collisions.

The effective rate coefficients for the reactions 32–48 from the literature review are provided in Table 5. The complete nine-level model is made up of Eqs. (33), (34), (35), (40), (41), (42), (46), (47), and (48).

Table 5 Full table of kinetic rates for potassium
Full size table

4 Steady-state and integrated rate solutions

The simplified rate equations can be solved analytically, as we assumed that the population in the higher lying states did not affect the population in the three laser levels. The steady-state solutions for the lowest three states and the intracavity laser intensity are

$$\begin{aligned} n_1= & {} \frac{(\frac{\sigma _{13}\varOmega }{2h\nu _p}+\gamma _3)n_3 +(\frac{\sigma _{12}\varPsi }{h\nu _l}+\gamma _2)n_2}{\frac{\sigma _{13}\varPsi }{h\nu _p} +\frac{\sigma _{12}\varPsi }{h\nu _l}}, \end{aligned}$$
(49)
$$\begin{aligned} n_2= & {} \frac{\frac{\sigma _{12}\varPsi }{h\nu _l}n_1+\gamma _{32}n_3}{\frac{\sigma _{12}\varPsi }{h\nu _l}+\gamma _2+2\gamma _{32}e^{-\theta }}, \end{aligned}$$
(50)
$$\begin{aligned} n_3= & {} \frac{2\gamma _{32}e^{-\theta }n_2+\frac{\sigma _{13}\varOmega }{2h\nu _p}n_1}{\frac{\sigma _{13}\varOmega }{h\nu _p}+\gamma _{32}e^{-\theta }+\gamma _3}, \end{aligned}$$
(51)
$$\begin{aligned} \varPsi= & {} \eta _0I_{\text {sat}}(\alpha \frac{\varOmega }{I{\text {sat}}}-B), \end{aligned}$$
(52)

where

$$\begin{aligned} \alpha= & {} \frac{(\frac{\sigma _{21}n}{g_{\text {th}}})(2\kappa (1-e^{-\theta })(\frac{\gamma _{31}}{\gamma _{21}})-1)-(3+2(1+3e^{-\theta })\kappa (\frac{\gamma _{31}}{\gamma _{21}}))}{2[(1+\kappa (1-e^{-\theta }))+2\frac{\varOmega }{I_{\text {sat}}}]} \end{aligned}$$
(53)
$$\begin{aligned} B= & {} \left( 1+\frac{\sigma _{21}n}{g_{\text {th}}}\right) \left( \frac{1+\kappa (1+2e^{-\theta } \frac{\gamma _{31}}{\gamma _{21}})}{\gamma _{21}}\right) 2[(1+\kappa (1-e^{-\theta }))\nonumber \\&+2\frac{\varOmega }{I_{\text {sat}}}] \end{aligned}$$
(54)
$$\begin{aligned} I_{\text {sat}}= & {} \frac{h\nu _p\gamma _{31}}{\sigma _{31}}. \end{aligned}$$
(55)

These equations can be solve simultaneously, to get the decoupled solutions as a function of \(\varOmega\). The pump intensity required to create the value for \(\varOmega\) is

$$\begin{aligned} I_p=\varOmega \frac{\sigma _{31}(n_3-2n_1)l_g}{e^{\sigma _{31}(n_3-2n_1)2l_g}-1}. \end{aligned}$$
(56)

In practice, \(I_p\) is known and \(\varOmega\) is to be computed, but the model is more easily run in reverse: finding the roots of Eqs. (49)–(52) and then using Eq. (56) to solve for the pump intensity required. The results of this are presented by Hager et al. [1, 13].

The rest of the energy levels have similar steady state answers:

$$\begin{aligned} n_4= & {} \frac{k^p_4*n_3^2+\frac{\sigma ^4_L}{h\nu _p}(\varOmega +\varPsi )(n_2+n_3)}{k_{4}^{PI}n_3 +\frac{\sigma _4^{ph}}{h\nu _p}(\varOmega +\varPsi )+\gamma _4}, \end{aligned}$$
(57)
$$\begin{aligned} n_6= & {} \frac{k^p_6*n_3^2+\frac{\sigma _L^6}{h\nu _p}(\varOmega +\varPsi )(n_2+n_3)}{k_{6}^{PI}n_3 +\frac{\sigma _6^{ph}}{h\nu _p}(\varOmega +\varPsi )+\gamma _6}, \end{aligned}$$
(58)
$$\begin{aligned} n_5= & {} \frac{k^p_5*n_3^2+\gamma _{45}n_4+\gamma _{65}n_6}{k_{6}^{PI}n_3 +\frac{\sigma _6^{ph}}{h\nu _p}(\varOmega +\varPsi )+\gamma _6}, \end{aligned}$$
(59)
$$\begin{aligned} n^+= & {} \frac{k^{PI}(n_2+n_3)n^{**}+\frac{\sigma ^{ph}}{h\nu _p}(\varOmega +\varPsi )n^{**}}{k_aMN}, \end{aligned}$$
(60)
$$\begin{aligned} n_2^+= & {} \sqrt{\frac{k_aMNn^+}{k_{DR}}}, \end{aligned}$$
(61)
$$\begin{aligned} n_7= & {} \frac{k_{DR}n_2^+(n_2^++n^+)}{\gamma _7}. \end{aligned}$$
(62)

Due to the rapid nature of three body association, Eq. (61) has assumed \(n_2^+>>n^+\) and been simplified accordingly.

5 Model predictions

Figure 9 shows the ratio of \(\delta\) (first defined in Eq. 36) to the alkali density as a function of total alkali density at many different buffer gas pressures, in the CW regime using the baseline rate parameters of Table 5 and \(\varOmega =19.3\, \text {kW}\,\text {cm}^{-2}\). At low alkali density, when photo-excitation dominates, \(\delta\) grows slower than total density, and the curves trend downward. Since photo-excitation processes dominate, ion density is both created and destroyed as a linear function of total alkali density, and additional alkali does not create more ions. Because dimer growth depends directly on the ion density, the dimer grows sub-linearly with respect to N and \(\delta\) grows slower than total density. However, at higher density, when the rate of collisional processes grow, ion creation goes like the square of alkali density and adding alkali causes an increase in ions, resulting in \(\delta\) growth that is super-linear with N. In general, adding helium causes the delta fraction to decrease and delays the take over of the collisional mechanisms. Most DPAL systems operate with \(N<10^{14} \, \text {cm}^{-3}\), and the population in higher lying states is less than \(6\%\) of the total. The perturbation approach to the three-level system appears appropriate for normal operating conditions.

Fig. 9
figure 9

Fraction of population in higher lying states as a function of alkali density for a series of helium densities. The dashed lower line represents the curve at a helium pressure of 4.82 Torr and the dotted upper line represents helium pressure of 4820 Torr. The lines in between represent helium density increasing by a factor of 1.15, with the bold red line corresponding to 760 Torr

Full size image
Fig. 10
figure 10

Delta fraction as a function of pump intensity and alkali density. The dotted line here represents an alkali density of \(1\times 10^{13}\, \text {cm}^{-3}\) and the dashed has an alkali of \(1\times 10^{16}\, \text {cm}^{-3}\). The lines in between represent alkali density increasing by a factor of 20. At low N, photo-processes dominate and \(\delta\) grows rapidly with pump intensity

Full size image

Figure  10 demonstrates this \(\delta\) fraction as a function of pump intensity at a fixed helium pressure of 1 atm. At high N, the ion concentration is dominated by Penning ionization, and adding pump intensity does little to the excited population. When density is low, \(N<\sim 10^{13}\), though, the excitation processes are dominated by photo effects and population in the higher lying states rises dramatically. Current diode technology limits pump intensity to \(<50\, \text {kW}\,\text {cm}^{-2}\) and again, the fraction of population in the higher lying states is limited to \(\sim 7\%\).

At high alkali densities and low pump intensity the delta fraction in Fig. 10 is constant with respect to pump intensity. This is due to energy pooling acting as the dominant mechanism. As pump intensity increases, though, photo-excitation processes grow and begin to take over as the largest contributor. Figure 11 demonstrates at what alkali densities and pump intensities each of the two excitation mechanisms are dominant in producing \(n_6\) density, at different buffer gas pressures. Each line represents when the energy pooling rate and the photon excitation rate are equal; at 760 Torr (blue), 1520 Torr, (orange), and 3800 Torr (yellow). As alkali density rises, more pump intensity is required to match the two rates, however increasing the buffer gas pressure decreases the pump required for all alkali densities. The slope of these lines are the ratio of the excitation cross-section and the pooling rate coefficient, going like \(\propto k_6^p/\sigma _L^6\).

Fig. 11
figure 11

Pump intensity required to match the wing absorption rate to the energy pooling rate, as a function on number density, at \(P=760\) (blue), 1520 (orange \({-}{-}\)), and 3800 (yellow \(\bullet\)) Torr

Full size image

As mentioned above, the quenching rates out of the intermediate states have not been experimentally observed. Figure 12 demonstrates the effect changing these rates has on the model. It shows the change in total \(\delta\) if \(k_4\) (blue), \(k_5\) (orange), and \(k_6\) (yellow) is changed. This is shown at the base line conditions from Table 2 at \(I=10\, \text {kW}\,\text {cm}^2\). Decreasing any of the quenching rates increases \(\delta\), but only increasing \(k_5\) causes a noticeable decrease. Much of the quenching from \(n_4\) and \(n_6\) terminates into \(n_5\), so it does not decrease the total \(\delta\), just the composition. Increasing the rate out of \(n_5\), though, sends population back into the lasing levels.

Fig. 12
figure 12

The change in \(\delta\) is plotted as a function of the change in the quenching rates. Modulating the \(k_4\) is in blue, \(k_5\) is in orange (\({-}{-}\)), and \(k_6\) is in yellow (\(\bullet\))

Full size image

Using the model created by Hager et. al, a prediction of laser intensity can be calculated as a function of alkali density, for a given laser design. Figure  13 displays the output laser intensity of a longitudinally pumped, static, CW DPAL, with geometry as described in [1], with a gain length of \(l_g=10\, cm\) and a threshold gain of \(g_{\text {th}}=0.086\,\text {cm}^{-1}\), shown as the solid line. The pump intensity is set to \(I_p= 10\, \text {kW}\,\text {cm}^2\) at a buffer gas pressure of 1 atm of pure helium, at \(T=460\) K setting \(\kappa =279.8\). For \(N<3\times 10^{12}\, \text {cm}^{-3}\), bleached gain is less than cavity losses, and no lasing is achieved. There is an optimum alkali density at \(n=1.66\times 10^{13}\, \text {cm}^{-3}\) after which the lasing decreases, as absorption in the cell becomes too large. The alkali density available to the lasing process including multi-level kinetics is reduced to \(N_{a}=N-\delta\). In Fig. 13, \(\delta /N = 0.0099\), and the intensity decreases by \(1.73\, \text {W}\,\text {cm}^2\) or \(<0.03\%\). If the fraction of the population in higher lying states were to increase (e.g. by increased wing absorption) the power loss also increases. The loss ratio is defined as 1 − (output power with multilevel kinetics/without multi-level kinetics), is illustrated by the dotted curve in Fig. 13. For example, if \(\delta /N=0.2\) at the peak output power, the loss ratio would be 0.235.

Fig. 13
figure 13

Three-level laser performance as a function of alkali density, at \(10\, \text {kW}\,\text {cm}^2\) pump intensity and 1 atm helium buffer gas. The solid vertical line represents the number density in which the intensity out is maximized and the dashed vertical line represents the alkali density available to lase if set to the maximum total alkali density and higher level kinetics are included. The magnitude of the degradation is shown with the loss ratio (\(\bullet\))

Full size image

The scaling of laser output intensity with pump intensity for the base line conditions is illustrated in Fig. 14, similar to the cases provided in Fig. 2. The bleached limit occurs near \(I_p= 20\, \text {kW}\,\text {cm}^2\), as the fine structure mixing rate limits output power and the system becomes bottle necked. At higher pump intensities, the production of higher lying states increases, \(\delta /N\) increases, and output power declines. At \(100\, \text {kW}\,\text {cm}^{-2}\) the degradation is significant with a loss factor of \(\sim 5\%\). The roll off of power exhibited at very high pump powers may be similar to that shown experimentally by Zhdanov et al. [9], but occurring at much higher intensities here. The rolloff exhibited at lower powers is likely not do to multi-level kinetics, but can be caused by any effect that drives the apparent alkali density down; diffusion due to temperature gradients in the alkali can cause \(\delta\) to increase.

Fig. 14
figure 14

Laser intensity as a function of pump intensity, with and without multi-level kinetics (\({-}{-}\)). The cases presented here are the same as in fig:PsiOmega. The blue is consistent with the parameters in Table 2, the alkali density is doubled for the green and the helium density is doubled for the red

Full size image

These figures illustrate the limited effect ionization has on laser power. The density of alkali available to lase decreases a small amount and that can have adverse effects on laser power. However this loss can largely be recovered by adding more alkali to the cell, to compensate for these deleterious processes. Due to the imperfect measurement techniques of alkali density, the \(\delta\) fraction may be lower than the error of the density measurement.

As mentioned above, one of the primary assumptions required to create this model was that \(\delta\) is a small perturbation of the lower three levels, only effecting the total population available to lase, such that the true alkali density is \(N_a=N-\delta\). Using this, the model should converge on a value of \(\delta\) when iterated. To do this, \(\delta\) is computed using the total alkali density. The alkali density is reduced by this value and a new \(\delta\) is recomputed. Figure 15 shows that it does converge. After the first iteration \(\delta\) is varied by \(<2.1\%\) and only \(<0.03\%\) after the second iteration.

Fig. 15
figure 15

The values of \(\delta\) as a function of alkali density at \(P=250\) Torr is iterated to assure convergence. The initial value is the blue solid line, the first iteration is the red dashes (\({-}{-}\)) and the second iteration is shown as black-filled circles (\(\bullet\))

Full size image

6 Conclusion

With the goal to resolve the controversy surrounding multi-level kinetics in a DPAL, a thorough literature review on mechanisms relevant to DPAL ionization has been conducted and the best rates of each process is provided. New scaling laws were developed to appropriately determine some rate constants, specifically, energy pooling, broadening of higher transitions, and Penning ionization. Some of these rates are well established in the literature, such as the spin-orbit mixing rates and the absorption cross-section of the pump and lasing transitions; others were found measured for potassium and are likely accurate, such as energy pooling and photoionization. Rates for Penning ionization, dimer formation and dissociative recombination have only been determined for other alkali metals. Quenching rates of the intermediates and absorption line shapes for high transitions have not been measured and require significant future study.

A new nine-level kinetic model has been produced adopting the most important mechanisms found in the literature. Using existing laser performance data as a guide, appropriate approximations allow for this model to be analytic and predict the population that has escape the lasing process as a function of laser system parameters. Population is excited to the intermediate states by both energy pooling and photo-excitation into the far wings of the absorption profile. The intermediates are then ionized mostly through Penning and photo-ionization. Atomic ions quickly undergo a three body collision that forms the ionic dimer, and dissociative recombination populates the Rydberg states. The Rydberg states radiate and quench in a cascading fashion back to the ground state.

The model predicts small values for \(\delta /N\), between 1 and 12% depending on laser parameters, and recommends methods to mitigate any adverse effects on laser power. The ionic dimer is a major component of \(\delta\), when the suggested rates are used. If not for this large dimer population, a simpler four-level model would be possible. Florescence measurements during high-power DPAL operation are in progress and will provide an important benchmark for the proposed model.