1 Introduction

LIBS is an atomic emission spectroscopy method in which, through a spectrum emitted by laser-generated plasma, one can identify constituent elements of the material and determine their concentrations in the sample. LIBS can be carried out in real time and in situ with little or even no sample preparation. In this method, a very transient microplasma is created on or in the sample by irradiating a laser pulse with appropriate wavelength, intensity, and pulse duration. The plasma light, in addition to a broad-band continuum which is due to braking radiation and recombination of electrons and ions, consists of ionic and atomic emission lines and even molecular emission bands. The best emission spectrum is associated with the maximum amount possible of signal-to-noise and signal-to-background ratios. Typically, quantitative analysis in LIBS is performed by three ways; calibration-free technique [1,2,3,4,5,6,7], calibration-based method [8,9,10,11,12], and the procedure of internal reference standard [13, 14]. In the first approach, to carry out quantitative analysis, in addition to three hypotheses of stoichiometric ablation, local thermodynamic equilibrium, and optically thin plasma, it is necessary to detect at least one spectral line with a suitable signal-to-noise ratio for each element of the sample. Moreover, in a calibration-based method, one or more standard samples are required with a matrix exactly similar to that of the target sample, which is not always possible. In the method based on internal reference standard, concentration of one of the constituent elements of the target substance must already be known or a specific element with a known concentration must be added to that as a reference. Hence, in this method, there are not the problems related to the other methods.

Photon flux of some resonant lines which are optically thick, before reaching the detector, is repeatedly re-absorbed and re-emitted by the same unexcited species in the plasma. This self-absorption effect, which, in many cases, results in a significant decrease in the spectral line photon flux, causes a serious error in calculating concentrations through the conventional LIBS method. In 2001, Lazic et al. [15] propounded a calibration curve-based model of a homogeneous plasma, assuming that LTE conditions are established. They proved that concentration of each element can be estimated by two linear and nonlinear terms, which the former describes an optically thin plasma and the latter is related to self-absorption effect demonstrating an optically thick plasma. In 2005, El Sherbini et al. [16] indicated that the ratio of the actual photon flux and width of an emission line to those corresponding to optically thin line can be expressed in terms of fractional powers of the self-absorption coefficient (SA) provided that SA > 0.2. In 2006, Bredice et al. [17] evaluated the self-absorption of Mn lines using equations introduced by El Sherbini et al. which relate photonic flux and width of spectral lines to the self-absorption coefficient. They examined the self-absorption effect with various approximations without the need for Stark coefficients using the photonic fluxes ratio of two spectral lines of a species. In addition, in 2009, Sun et al. [18] obtained self-absorption coefficients of spectral lines using the ratio of photon flux of each spectral line to that of a reference spectral line of the same species having a very low self-absorption. In this procedure, in addition to that the self-absorption coefficient of reference line is considered to be one, the width of each line must also accurately be measurable. In the previous work [19], a peak intensity-based model of spectral lines, in which their widths are assumed to be the same, was developed. In this method, the plasma temperature is initially corrected through step-by-step correction of photonic fluxes using a recursive algorithm to the step that the self-absorption coefficient, with a good approximation, approaches one. Then, by the use of the non-self-absorbed photon fluxes, the analyte concentration is calculated through the conventional equations of LIBS using calibration-free method.

The importance of calcium in the diet is undeniable. The lack of this mineral, which is found to be abundant in dairy products, causes a variety of problems including osteoporosis, which is more common among middle-aged and older women. This fact signifies that other sources of calcium should be better known. Moreover, many researches indicate that most green vegetables are rich in calcium [20,21,22,23,24]. Nowadays, for different reasons, including gastrointestinal problems due to lactose intolerance in dairy products, it seems the need for the use of these plants as calcium-rich references is necessary. Of all the plants rich in calcium, not only do fennel, dandelion, spinach, parsley, and bay leaf have numerous nutritive, healing, and medicinal features, but they also use extensively on a regular basis. Hence, it appears that they are appropriate candidates for study.

In this research, calcium concentration related to the leaf of five plants of fennel, bay leaf, dandelion, spinach, and parsley is determined by LIBS process using IRS method. To calculate the concentration of analyte, depending on which emission lines associated with neutral or ionic species of the analyte and the reference are used, four different formulas can be applied. To correct self-absorption effect, the peak intensity-based model is used [19]. To achieve more accurate results, in addition to correcting self-absorption effect for the emission lines used in calculating the plasma temperature and the analyte concentration, one can show that this correction should also be carried out for lines which are indirectly influenced on the calculation of electron density. The electron density is obtained from the Saha–Boltzmann statistics using calcium emission lines as the analyte. Calculations indicate that there is a significant difference in the value of the electron density before and after correcting self-absorption effect.

2 Theoretical

Since various plants consist of a significant number of elements many of which may be unknown, in this case, quantitative analysis is not possible using calibration-free method. On the other hand, to establish an appropriate calibration curve, fabrication of several standard samples with similar matrices is quite difficult and time-consuming. Therefore, in this case, IRS method is more suitable for achieving the concentration of unknown elements.

2.1 Internal reference standard method

Conventional detectors used in LIBS experiments, instead of the intensity of emission lines, measure the spectral photon flux; that is, the number of photons emitted per unit time, per unit area, and per unit wavelength. On the other hand, due to different mechanisms of broadening in spectral lines, the use of spectrally integrated signal known as “photon flux” instead of “spectral photon flux” is more appropriate. In a laser-generated plasma without considering self-absorption effect, the integral signal (\(\bar{S}_{\text{A}}^{i, 0}\)) related to one of emission lines of a neutral \(\left( {i = {\text{I}}} \right)\) or ionized \(\left( {i = {\text{II}},{\text{III}}, \ldots } \right)\) atom of the analyte A can be expressed as follows [19]:

$$\bar{S}_{\text{A}}^{i, 0} \equiv \mathop \int \limits_{{\lambda_{ul} - \infty }}^{{\lambda_{ul} + \infty }} S_{\text{A}}^{i, 0} \left( \lambda \right){\text{d}}\lambda = F\left( {\frac{{A_{\text{ul}}^{i} g_{\text{u}}^{i} }}{{U^{i} \left( T \right)}}} \right)_{\text{A}} n_{\text{A}}^{i} \exp \left( { - \frac{{E_{\text{u}}^{i} }}{{k_{\text{B}} T}}} \right)_{\text{A}} ,$$
(1)

where the superscript “zero” signifies that the measurement is in the absence of self-absorption, \(A_{ul}^{i}\) is the transition probability \(({\text{s}}^{ - 1} )\) between the upper level \(\left( u \right)\) and the lower level \(\left( {\text{l}} \right)\), \(\lambda_{\text{ul}}\) is the central wavelength of the transition, \(g_{\text{u}}^{i}\) is the degeneracy of the upper level (dimensionless), \(n_{\text{A}}^{i}\) is the population of the species, i, of the element A \(\left( {{\text{m}}^{ - 3} } \right)\), \(E_{\text{u}}^{i}\) is the energy of the upper level \(\left( {\text{J}} \right)\), \(k_{\text{B}}\) is the Boltzmann constant \(\left( {{\text{JK}}^{ - 1} } \right)\), \(T\) is the plasma temperature \(\left( {\text{K}} \right)\), \(U^{i} \left( T \right)\) is the partition function of the species, i, (dimensionless), and \(F\) is an experimental parameter \(\left( {\text{m}} \right)\) that depends on the optical efficiency of the collection system, the density, and volume of the plasma. Since spectral photon flux of each emission line is proportional to its intensity, for the sake of simplicity of expression, and not in calculations, from now on, the word “intensity” is used instead of “spectral photon flux”. To determine concentration of elements by LIBS method, in addition to the concentration of atomic species \(C_{\text{A}}^{\text{I}}\), ionic ones \(\left( {C_{\text{A}}^{\text{II}} ,C_{\text{A}}^{\text{III}} , \ldots } \right)\) must also be specified in the plasma. This is to reason that concentration of each element (for example A) in the sample, assuming stoichiometric ablation, is given by the following:

$$C_{\text{A}} = C_{\text{A}}^{\text{I}} + C_{\text{A}}^{\text{II}} + C_{\text{A}}^{\text{III}} + \cdots$$
(2)

In LIBS, the concentration often implies the mass fraction; that is, the ratio of the density of element A, \(\rho_{\text{A}}\), to the density of total mixture \(\rho_{\text{tot}}\), defined as \(C_{\text{A}} \equiv \rho_{\text{A}} /\rho_{\text{tot}}\). In addition, the concentration of ionized atoms with the ionization states greater than one, in the normal range of exciting laser energy which is applied for LIBS experiments, can be ignored very often, and accordingly, Eq. (2) can be written as follows:

$$C_{\text{A}} \cong C_{\text{A}}^{\text{I}} + C_{\text{A}}^{\text{II}} .$$
(3)

On the other hand, since intensity of ionic lines is normally significantly smaller than the atomic ones, without any intensified CCD, intensity of ionic lines is not signally detectable very often. In this case, the number density of once-ionized atoms, \(n_{\text{A}}^{\text{II}}\), can be derived in terms of that of the neutral atoms, \(n_{\text{A}}^{\text{I}}\) via the Saha equation [25]:

$$R_{\text{A}}^{\text{I}} \equiv \frac{{n_{\text{A}}^{\text{II}} }}{{n_{\text{A}}^{\text{I}} }} = \frac{{\left( {2\pi m_{\text{e}} k_{\text{B}} T} \right)^{3/2} }}{{n_{\text{pe}} h^{3} }}\frac{{2U^{\text{II}} \left( T \right)}}{{U^{\text{I}} \left( T \right)}}\exp \left( { - \frac{{E_{\text{ion}} }}{{k_{\text{B}} T}}} \right) .$$
(4)

In Eq. (4), \(U^{\text{I}} \left( T \right)\) and \(U^{\text{II}} \left( T \right)\) are the partition functions of neutral and once-ionized states, respectively, \(m_{\text{e}}\) is the electron mass, \(n_{\text{pe}}\) is the plasma electron density, and \(E_{\text{ion}}\) is the ionization potential energy of the atom in transition from the ground level of the neutral state to the ground level of the once-ionized state.

Therefore, from Eqs. (3) and (4) and also the definitions of \(C_{\text{A}}^{\text{I}} \equiv \frac{{\rho_{\text{A}}^{\text{I}} }}{{\rho_{\text{tot}} }} = \frac{{m_{\text{A}}^{\text{I}} n_{\text{A}}^{\text{I}} }}{{\rho_{\text{tot}} }}\), \(C_{\text{A}}^{\text{II}} \equiv \frac{{\rho_{\text{A}}^{\text{II}} }}{{\rho_{\text{tot}} }} = \frac{{m_{\text{A}}^{\text{II}} n_{\text{A}}^{\text{II}} }}{{\rho_{\text{tot}} }}\) and \(\frac{{C_{\text{A}}^{\text{II}} }}{{C_{\text{A}}^{\text{I}} }} = \frac{{m_{\text{A}}^{\text{II}} }}{{m_{\text{A}}^{\text{I}} }}R_{\text{A}}^{\text{I}}\) (where \(m_{\text{A}}^{\text{I}}\) and \(m_{\text{A}}^{\text{II}}\) are masses of neutral and once-ionized states of the element A, respectively), \(C_{\text{A}}\) can be calculated from the following way (it should be emphasized that although \(m_{\text{A}}^{\text{I}}\) and \(m_{\text{A}}^{\text{II}}\) can practically be assumed the same, they are theoretically different to the extent of one electron):

$$C_{\text{A}} = C_{\text{A}}^{i} \left[ {1 + \left( {\frac{{C_{\text{A}}^{\text{II}} }}{{C_{\text{A}}^{\text{I}} }}} \right)^{p} } \right] = C_{\text{A}}^{i} \left[ {1 + \left( {\frac{{m_{\text{A}}^{\text{II}} }}{{m_{\text{A}}^{\text{I}} }}R_{\text{A}}^{\text{I}} } \right)^{p} } \right] .$$
(5)

In Eq. (5), \(C_{\text{A}}\) can be expressed in terms of the concentration of neutral (if \(i = {\text{I}}, p = 1\)) or once-ionized (if \(i = {\text{II}}, p = - 1\)) atoms.

Now, from the definitions of \(C_{\text{A}}^{\text{I}}\) and \(C_{\text{A}}^{\text{II}}\) and using Eqs. (1) and (5), one can derive the following:

$$\bar{S}_{\text{A}}^{i, 0} = \left\{ {F\rho_{\text{tot}} \left[ {\frac{{A_{\text{ul}}^{i} m_{\text{A}}^{i} g_{\text{u}}^{i} }}{{U^{i} \left( T \right)}}\exp \left( { - \frac{{E_{\text{u}}^{i} }}{{k_{\text{B}} T}}} \right)} \right]_{\text{A}} \bigg /\left( {1 + \left( {\frac{{m_{\text{A}}^{\text{II}} }}{{m_{\text{A}}^{\text{I}} }}R_{\text{A}}^{\text{I}} } \right)^{p} } \right)} \right\}C_{\text{A}} ,$$
(6)

where, depending on whether the spectral line of the analyte is related to the neutral state or the once-ionized one, the values of \(i\) and \(p\) must be considered equal to \(\left( {i = {\text{I}}, p = 1} \right)\) or \(\left( {i = {\text{II}}, p = - 1} \right)\), respectively. In Eq. (6), the value \(\bar{S}_{\text{A}}^{i,0}\) is experimentally obtained from the plasma emission spectrum, while other quantities, except the product of \(F\rho_{\text{tot}}\), can be extracted from standard library databases (e.g., National Institute of Standards and Technology, NIST) [26]. If \(F\rho_{\text{tot}}\) can be obtained in some way, concentration of the analyte will also be calculated. For this purpose, since the unknown value of \(F\rho_{\text{tot}}\) is the same for all species, by considering an element as IRS whose concentration \(\left( {C_{\text{R}} } \right)\) is already known, one can calculate this quantity using each arbitrary line of the internal reference from an equation similar to Eq. (6) with new indices of \(j\) and \(q\) instead of \(i\) and \(p\).

Accordingly, after a bit of simple calculation, concentration of the analyte can be obtained by the following:

$$C_{\text{A}} = \frac{{\bar{S}_{\text{A}}^{i, 0} }}{{\bar{S}_{\text{R}}^{j, 0} }}\frac{{\left[ {\frac{{m^{i} U^{i} \left( T \right)}}{{A_{\text{ul}}^{i} g_{\text{u}}^{i} }}\exp \left( {\frac{{E_{\text{u}}^{i} }}{{k_{\text{B}} T}}} \right)} \right]_{\text{A}} \left( {1 + \left( {\frac{{m_{\text{A}}^{\text{II}} }}{{m_{\text{A}}^{\text{I}} }}R_{\text{A}}^{\text{I}} } \right)^{p} } \right)}}{{\left[ {\frac{{m^{j} U^{j} \left( T \right)}}{{A_{\text{ul}}^{j} g_{\text{u}}^{j} }}\exp \left( {\frac{{E_{\text{u}}^{j} }}{{k_{\text{B}} T}}} \right)} \right]_{\text{R}} \left( {1 + \left( {\frac{{m_{\text{R}}^{\text{II}} }}{{m_{\text{R}}^{\text{I}} }}R_{\text{R}}^{\text{I}} } \right)^{q} } \right)}}C_{\text{R}} .$$
(7)

Equation (7) indicates that the analyte concentration can be calculated from four different manners (Table 1) depending on how neutral or once-ionized lines of the analyte and the reference are exploited.

Table 1 Different ways of the use of Eq. (7) to calculate concentration of the analyte
Full size table

Having found \(R\) (that is, \(R_{\text{A}}^{\text{I}}\) and \(R_{\text{R}}^{\text{I}}\)), the concentration can be calculated. The above equations are all used in the standard form which is correct in the absence of self-absorption, while most of the elements in the plants are usually influenced by self-absorption effect. Therefore, to calculate concentration of each element, correction of self-absorption effect is practically necessary, which will be discussed in the later sections.

3 Experimental

Although, in LIBS experiments, especially by calibration-free method, it is generally asserted that there is no need for the preparation; in calibration-based approach and IRS method, preparation of the samples is inevitable. Furthermore, since some of characteristics of the stimulating laser light in the sample location, including intensity, depend on the distance between the laser and the sample and also on the cross-section area of the laser light on the sample location, to achieve the best result in LIBS process, it is very important and essential how the laser is positioned relative to the other optical components. Hence, in the following, sample preparation and laboratory set-up will be discussed.

3.1 Sample preparation

As mentioned earlier, in this research work, calcium concentration of the leaf of five plants, fennel, bay leaf, dandelion, spinach, and parsley is examined by the method of IRS. For this purpose, the leaf of plants was initially washed and then dried in the open air and the ambient temperature. Considering that, in the plants in question, concentration of copper is very low compared to that of other elements; and since it is expected, some spectral lines of copper, owing to being non-resonant and having low transition probabilities, have very low self-absorption in the normal range of plasma temperatures (\(< 8000 {\text{K}}\)), this element was selected as IRS. After being completely dried the leaves, they were milled by a blade grinder up to reaching powders with the size of sub-micron. Then, the copper (nanopowder, 60–80 nm particle size from Sigma-Aldrich) was added to each of the above plants by 6 wt%. An analytical balance (Mettler Toledo) with four decimal places was used to measure mass of materials. The total mass of all specimens and the mass (concentration) of IRS in each specimen were measured to four decimal places constant and equal to 2.0000 g and 0.1200 g (6.00 wt%), respectively. Each specimen, containing mixture of the sub-micro powders of copper as IRS and the corresponding plant was poured into a vial and well mixed together by shaking the vial for 5 min. Then, from each specimen, a cylindrical tablet with a diameter of 2 cm and a thickness of 5 mm was fabricated under 400 bar pressure using a custom-made mold designed for this purpose.

3.2 Laboratory set-up

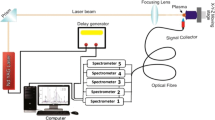
Figure 1 shows a schematic diagram of the LIBS experiment utilized in this research. The Q-switched, Nd:YAG pulsed laser (λ = 1064 nm, from Quantel) generates a laser pulse with duration, maximum energy, and repetition rate of 6 ns, 900 mJ, and 10 pulse/s, respectively. The focal length of the converging lens is 20 cm. Hence, with the laser pulse energy of 100 mJ and considering the effective diameter of the laser beam on the lens that is ~ 8 mm, the power density on the sample will approximately be derived equal to 3.7 × 1011 W cm−2. For the best adjustment in each experiment, the sample and the optical fiber were placed on two distinct adjustable XYZ manual micropositioners. The plasma emission spectrum is transmitted via a collimating lens into the optical fiber connected to the spectrometer) The compact spectrometer “SpectraStar” Model S150) with the electronic and optical resolutions of 0.16 nm and 0.44 nm, respectively. The delay generator (Stanford Research Systems, Model DG645) supplies the minimum gate delay (about 2 μs) in which the background is excluded. With this delay time, it is assumed that LTE condition is fulfilled [27,28,29,30]. The trigger signal is provided by the synchronous output of laser power supply. Due to probable inhomogeneity of the material at the surface and in the volume of the sample, five points of each sample were irradiated by five laser shots and the average of all 25 spectra was considered to analyze the material. Prior to each measurement, three laser shots were applied at each point to eliminate surface contamination.

Fig. 1
figure 1

Schematic set-up utilized in the LIBS experiment

Full size image

4 Results and discussion

Figure 2 indicates a typical plasma emission spectrum in this research work among 25 spectra measured for each leaf of plant (e.g., the leaf of parsley). After comparing wavelengths of the emission spectral lines with the confirmed information from standard databases (e.g., NIST), some lines associated with constituent elements of the material were identified. Some well-known spectral lines of calcium as the analyte and copper as IRS have been specified in the figure. Table 2 shows some spectroscopic information on the relevant transitions.

Fig. 2
figure 2

A typical emission spectrum of a laser-induced plasma related to the leaf of fennel (as a representative of all spectra)

Full size image
Table 2 Spectroscopic information of some species measured in the laser-induced plasma of the five leaves: \(\lambda_{\text{obs}} ({\text{nm}})\) is the wavelength observed from the spectrum in accordance with the reported values in the site of NIST; \(A_{ij} ({\text{s}}^{ - 1} )\) is the transition probability; \(E_{i} ({\text{eV}})\), \(E_{j} ({\text{eV}})\) and \(g_{i}\), \(g_{j}\) are the energies and the degeneracies of the lower and upper levels, respectively
Full size table

Sometimes, identification of some spectral lines associated with various species of the material, due to low resolution of spectrometers and overlap of spectral lines, is not possible. Assuming correct identification of the spectral lines, in many cases, one still cannot expect that the results obtained from the conventional calculations of LIBS are consistent with reality especially in relation to the plasma temperature and the electron density. There are several reasons for this inconsistency, including self-absorption phenomenon, lack of LTE condition, and inadequate time to collect light particularly when the sensitivity of the spectrometer detector is low. Of all these effective factors, self-absorption phenomenon more markedly affects the final results. As seen from Table 2, not only are the spectral lines of copper non-resonant, but they also have relatively low transition probabilities. Hence, as expected and the calculations also confirm (the self-absorption coefficients (SA), in the first step, are much close to 1), these spectral lines are, to a great extent, non-self-absorbed and, thus, very suitable for calculating the temperature.

After identifying the spectral lines of calcium and copper (Table 2), the spectral photon flux at the central wavelength of each line was measured. Since the copper lines are fortunately approximately non-self-absorbed, assuming LTE condition, the plasma temperature was calculated using copper lines through two ways: the line-pair ratio (LPR) method by the use of two pairs of copper spectral lines (510.55 nm, 515.32 nm) and (510.55 nm, 521.82 nm), and the Boltzmann plot (BP) by applying all of the three neutral lines (Fig. 3, dark red line). These calculations were performed by exploiting the results derived from the average of 25 measured spectra for each sample. The amount of temperatures obtained from both ways for plant specimens, considering the laser energy (100 mJ/pulse), appears to be quite reasonable (the column 3 of Table 3).

Fig. 3
figure 3

Boltzmann plots associated with fennel (as a representative of the five plants)

Full size image
Table 3 The temperature and the density of the laser-produced plasma related to the five leaves using the average of 25 different spectral photon fluxes, measured for each sample: \(T_{{{\rm p}({\text{Cu}})}}\) is the plasma temperature calculated by copper lines; \(T_{{{\rm p}\left( {\text{Ca}} \right){\text{-BSAC}}}}\), \(T_{{{\rm p}\left( {\text{Ca}} \right){\text{-ASAC}}}}\) and \(n_{{{\rm p}\left( {\text{Ca}} \right){\text{-BSAC}}}}\), \(n_{{{\rm p}\left( {\text{Ca}} \right){\text{-ASAC}}}}\) are the plasma temperatures and the plasma electron densities, calculated by calcium lines before and after self-absorption correction, respectively; BP and LPR indicate the methods of Boltzmann plot and line-pair ratio, respectively
Full size table

On the other hand, it is expected that the plasma temperature calculated from calcium lines to be also equal to what was obtained from copper lines. To check the correctness this point, the plasma temperature was also calculated by calcium lines from both LPR and BP methods (Table 3, the column 4). In the LPR method, five suitable pairs of calcium lines (317.93 nm, 393.37 nm), (317.93 nm, 396.85 nm), (373.69 nm, 393.37 nm), (373.69 nm, 396.85 nm), and (422.67 nm, 558.88 nm) were exploited. In this case, it should be noted that some spectral lines of the same species, due to the closeness of their upper energy levels, establish a serious error in calculating the plasma temperature [31]. Hence, among all the identified lines, only those have a significant difference in their upper energy levels were selected to calculate the temperature.

In the BP method, as depicted in Fig. 3 (dark green and blue lines), there are two options to achieve the temperature, depending on whether the ionic lines or the neutral lines of calcium to be employed. The difference between these two temperatures, as obviously seen from the slope of relevant Boltzmann plots, is considerable. This is to the reason that the neutral line of 422.67 nm is much more self-absorbed than the ionic lines of 393.37 nm and 396.85 nm. Anyway, the average of the temperatures obtained from the two plots is the calcium temperature index and has been inserted in the column 4 of Table 3. As observed from Table 3, not only have the temperatures obtained from calcium lines through LPR and BP a dramatic difference with each other, but they also have a significant difference with those derived from copper lines. Here, it should be emphasized that the dramatic difference of temperatures in the two methods of LPR and BP is due to the fact that, in the BP method, all of identified lines, whether self-absorbed or non-self-absorbed, are used; while, in the LPR method, due to the limitation related to the energy difference of upper levels, only a limited number of spectral lines are usable. Since, in the calculation of plasma temperature, the BP method is more reliable than the LPR one, from here up to the end of the paper, the BP temperature will be utilized for other calculations.

Having determined the temperatures, the partition functions of once-ionized and neutral species of both calcium and copper were specified through the database of NIST. Prior to obtaining the value of \(R\) associated with calcium and copper, the electron density has to be calculated. For this purpose, the electron density was calculated in 28 different states by the Saha equation [Eq. (4)] using four ionic and seven neutral lines of calcium (according to Table 2). Then, the average of these 28 results was considered as the final electron density (the column 6 of Table 3).

All calculations, up to this stage, were carried out using the MATLAB program. The concentration of copper as IRS was considered equal to 6 wt% in all samples. The energy of ionization potential and some other quantities related to calcium and copper such as the atomic mass, the degeneracy, etc. were extracted from NIST and other library databases [26, 32].

In this step, the concentration of calcium as the analyte was computed by Eq. (7) in 33 states using 11 calcium lines (whether neutral or once-ionized) and three copper lines, and then, the average of the above results was accounted and considered as the final calcium concentration for each of the five selected leaves (the column two of Table 4).

Table 4 Calcium concentration of the five leaves: \(C_{\text{Ca-BSAC}}\) and \(C_{\text{Ca-ASAC}}\) indicate the calcium concentration computed by the method of LIBS before and after self-absorption correction, respectively; \(C_{\text{Ca-ICP}}\) is the calcium concentration measured by ICP-OES method; \(\eta_{\text{BSAC}}\) and \(\eta_{\text{ASAC}}\) show the percentage relative error of the concentrations obtained from LIBS relative to ICP-OES before and after self-absorption correction, respectively
Full size table

On the other hand, to verify correctness of the results obtained from the LIBS experiment, calcium concentration of all five leaves was also measured by inductively coupled plasma optical emission spectrometry (ICP-OES). As observed in Table 4, there is a dramatic difference between the concentrations derived from LIBS without considering self-absorption correction and those from ICP-OES. This is certainly due to self-absorption effect. As mentioned earlier, the resonant transitions of calcium (corresponding to the wavelengths of 393.37 nm, 396.85 nm, and 422.67 nm) and even its near-resonant transitions (whose lower levels are very close to the ground state) are affected by self-absorption phenomenon; and hence, one can expect that a serious error is observed in the final results of the concentration. Since the spectral photon flux of the self-absorbed transitions is obviously smaller than that of the non-self-absorbed ones, the conventional calculations of LIBS can, no longer, be applied in these cases. Consequently, to achieve reliable and correct results, the correction of self-absorption effect is essential and inevitable.

To correct the self-absorption effect, the peak intensity-based model [18] was used. Assume that \(S_{\text{s}} \left( {\lambda_{\text{ul}} } \right)\) and \(S_{\text{s}}^{ 0} \left( {\lambda_{\text{ul}} } \right)\) are, respectively, self-absorbed and non-self-absorbed spectral photon fluxes related to the peak of an emission line of the s-th species. In this case, self-absorption coefficient \((SA)\) is defined as follows:

$${\text{SA}} \equiv \frac{{S_{\text{s}} \left( {\lambda_{\text{ul}} } \right)}}{{S_{\text{s}}^{0} \left( {\lambda_{\text{ul}} } \right)}}.$$
(8)

\({\text{SA}}\) can also be expressed in terms of the absorption coefficient of the emission line at the central wavelength, \(\alpha_{0}\), as follows [13]:

$${\text{SA}} = (1 - e^{{ - \alpha_{0} L}} )/\alpha_{0} L ,$$
(9)

where the product of \(\alpha_{0} L\) is the optical penetration depth at the central wavelength (\(L\) is a length of the plasma plume, in which the self-absorption occurs prior to any detection). In the absence of self-absorption; that is, when the line is optically thin, \({\text{SA}}\) is equal to one; while it decreases to zero as the line becomes optically thick. On the other hand, the width of emission line (\(\Delta \lambda\)) dramatically increases due to self-absorption effect. In the presence of self-absorption, \(\Delta \lambda\) is practically measured through the plasma spectrum, whereas the true width (non-self-absorbed width), \(\Delta \lambda_{0}\), is actually unknown and can be obtained by the following equation [19]:

$$\frac{\Delta \lambda }{{\Delta \lambda_{0} }} = \left[ {\alpha_{0} L/\ln \left( {\frac{2}{{1 + \exp \left( { - \alpha_{0} L} \right)}}} \right) - 1} \right]^{1/2} .$$
(10)

In emission spectra measured in the LIBS experiment, only the variables of each spectral line that can experimentally be measured are the spectral photon flux at the central wavelength, \(S_{\text{s}} \left( {\lambda_{\text{ul}} } \right)\), the width, \(\Delta \lambda\), and the photon flux \(\bar{S}_{\text{s}} \equiv \mathop \int \nolimits_{{\lambda_{\text{ul}} - \infty }}^{{\lambda_{\text{ul}} + \infty }} S_{\text{s}} \left( \lambda \right){\text{d}}\lambda \approx \Delta \lambda \times S_{\text{s}} \left( {\lambda_{\text{ul}} } \right)\), all of which are inevitably influenced by self-absorption effect.

Therefore, to obtain the non-self-absorbed variables which are essential in the conventional calculations of LIBS, foremost, the optical penetration depth (\(\alpha_{0} L\)), and then through Eq. 9, the self-absorption coefficient (\({\text{SA}}\)) must be computed. For this purpose, consider two spectral lines of a species with central wavelengths of \(\lambda_{{{\text{ul}}1}}\) and \(\lambda_{{{\text{ul}}2}}\) and different upper level energies, \(E_{{{\text{u}}1}} \ne E_{{{\text{u}}2}}\), whose spectral photon fluxes at their central wavelengths, \(S_{\text{s}} \left( {\lambda_{{{\text{ul}}1}} } \right)\) and \(S_{\text{s}} \left( {\lambda_{{{\text{ul}}2}} } \right)\), are much larger than the background. In this case, the optical penetration depths of the two spectral lines (\(\alpha_{01} L\) and \(\alpha_{02} L\)) are derived by the following two equations [19]:

$$\frac{{S_{\text{s}} \left( {\lambda_{{{\text{ul}}2}} } \right)}}{{S_{\text{s}} \left( {\lambda_{{{\text{ul}}1}} } \right)}} = \frac{{(\lambda_{\text{ul}}^{4} )_{1} }}{{(\lambda_{\text{ul}}^{4} )_{2} }}\frac{{1 - e^{{ - \alpha_{02} L}} }}{{1 - e^{{ - \alpha_{01} L}} }}\frac{{e^{{ - (E_{\text{u}} - E_{\text{l}} )/k_{\text{B}} T}} }}{{e^{{ - (E_{\text{u}} - E_{\text{l}} )/k_{\text{B}} T}} }},$$
(11)

and

$$\frac{{\alpha_{01} L}}{{\alpha_{02} L}} \cong \frac{{\left( {\lambda_{\text{ul}}^{4} A_{\text{ul}} g_{\text{u}} e^{{ - E_{\text{l}} /k_{\text{B}} T}} } \right)_{1} }}{{\left( {\lambda_{\text{ul}}^{4} A_{\text{ul}} g_{\text{u}} e^{{ - E_{\text{l}} /k_{\text{B}} T}} } \right)_{2} }}.$$
(12)

In the nonlinear Eqs. (11) and (12), all quantities, except the plasma temperature \(T\), can be obtained from library information or directly from the plasma emission spectrum. Therefore, to calculate the optical penetration depths of \(\alpha_{01} L\) and \(\alpha_{02} L\), the plasma temperature must first be calculated using experimental data by one of the common methods (the line-pair ratio, the Boltzmann plot, and so on). After calculating \(T\), \(\alpha_{01} L\), and \(\alpha_{02} L\), the self-absorption coefficients of both spectral lines, in the first approximation [\(\left( {{\text{SA}}_{1} } \right)_{1}\) and \(\left( {{\text{SA}}_{2} } \right)_{1}\)], must be derived from Eq. (9); and finally, by knowing the values of \(\left( {{\text{SA}}_{1} } \right)_{1}\) and \(\left( {{\text{SA}}_{2} } \right)_{1}\) and using Eq. (8), the non-self-absorbed spectral photon fluxes at the central wavelength are obtained in the first approximation (\({[S_{\rm s}^{0} ( \lambda_{{\rm ul}1} ) ]}_{1} \ {\text{and}} \ {[ {S_{\rm s}^{0}} (\lambda_{{\rm ul}2}]}_{1}\)). At this point, if self-absorption coefficient for each spectral line is equal to one, this means that there is no self-absorption for that line. Otherwise, by the use of the spectral photon fluxes modified in the previous stage, once again, all of the above calculations must be carried out, and this process continues as long as the self-absorption coefficient of each line, with a good approximation, becomes equal to one. In this case, the plasma temperature approaches a certain value and the spectral photon fluxes become much close to the non-self-absorbed ones. Here, it should be emphasized that since, for calculating the plasma temperature, the electron density, and even the concentration of analyte, the non-self-absorbed peak intensity [\(S_{\text{s}}^{0} \left( {\lambda_{\text{ul}} } \right)\)] and width (\(\Delta \lambda_{0}\)) are used, after self-absorption correction of spectral lines, these quantities must, respectively, be calculated from Eqs. (8) and (10).

Therefore, to improve the results derived from the previous step, according to the mentioned method, the self-absorption correction of 11 spectral lines of calcium (Table 2) was carried out using ten different binary combinations. The computations associated with self-absorption correction were performed by C++ programming language pursuant to the recursive algorithm proposed in Ref. [19]. Then, the plasma temperature was calculated using the non-self-absorbed spectral lines of calcium through the two methods of LPR and BP yet again (Fig. 3, magenta and blue lines and Table 3, the column 5). As seen, after self-absorption correction, the temperature obtained from the calcium lines through both methods of LPR and BP is very close to that was derived from the copper lines, which proves the vital role of the process of self-absorption correction. Moreover, it is clearly seen from Fig. 3 that all three linear curves related to the Boltzmann plots of the species of CuI, CaI, and CaII have been paralleled after correcting the self-absorption. This means that the plasma temperature is independent of the type of species provided that the self-absorption effect is corrected.

Having achieved the true plasma temperature, it is now time to calculate the real electron density. To gain this end, similar to before correcting the self-absorption, the electron density was again calculated by the Saha equation in 28 different states using the true intensities of four ionic and seven neutral lines of calcium. Thus, the average of the 28 outputs was eventually considered as the real electron density (the column 7 of Table 3). The electron density can also be calculated through Stark broadening of emission lines. However, it should be noted that here also except few lines such as \(H_{\alpha }\) line of hydrogen [33] which their signal-to-noise ratios are also normally very small, approximately the width of all spectral lines effectively increases under influence of self-absorption effect. This means that the process of self-absorption correction is eventually inevitable.

Besides the above quantities, to calculate the ratio R and the partition function of all species involved in the computation of calcium concentration, correcting the self-absorption was also considered. Finally, by exploiting the true (non-self-absorbed) quantities obtained from the previous steps, the calcium concentration was again calculated by Eq. (7) in 33 states using 11 calcium lines and three copper lines. Then, their mean was taken into account as the final concentration for each leaf (the column 3 of Table 4).

Comparison of the temperature, the electron density, and the calcium concentration associated with each leaf before and after the self-absorption correction signifies that the above quantities, after correcting the self-absorption, dramatically change and approach the true values (Tables 3, 4). The reason for this assertion is that the calcium concentrations of the five leaves after self-absorption correction are very close to those have been measured by ICP-OES.

As seen from Fig. 4, the self-absorption effect of calcium spectral lines (especially the resonant lines corresponding to the wavelengths of 393.37 nm, 396.85 nm, and 422.67 nm) causes an enormous increase in the plasma temperature compared to the case that the self-absorption is corrected. This increase in some samples is over than twice the expected temperature. By correcting self-absorption effect, the temperature decreases and substantially approaches the temperature achieved using the copper lines. This result was expected, because the self-absorption of copper lines used in calculating the plasma temperature is very low. Moreover, this result that the temperatures calculated using the spectral lines of different elements are equal is quite reasonable owing to the cumulative effect of plasma.

Fig. 4
figure 4

The plasma temperature calculated using: copper lines (green bar); calcium lines before self-absorption correction (red bar); calcium lines after self-absorption correction (blue bar)

Full size image

Figure 5 indicates that, by correcting the self-absorption effect, the electron density also decreases and ultimately amounts to a certain value. The reason for this behavior is that, after correcting self-absorption effect, the plasma temperature decreases which, in turn, leads to the reduction of local fluctuations and, consequently, the increase of mean free path of the plasma particles. With regard to calculating the electron density using the Saha–Boltzmann statistics, it is observed that the amount of electron density is changed by self-absorption effect in both direct and indirect forms. The self-absorption of the spectral lines of neutral and once-ionized calcium which are directly used in the calculation causes the direct influence; and change of the plasma temperature, R, and the partition function due to the self-absorption represents the indirect effect. In Fig. 5, due to the huge difference in the electron density before and after correcting the self-absorption, the ordinate is shown in two different scales relative to the center of the system.

Fig. 5
figure 5

The plasma electron density: before (blue bar) and after (green bar) self-absorption correction

Full size image

As observed in Table 4 and Fig. 6, calcium concentration of the five leaves obtained from the LIBS method before correcting self-absorption effect has a dramatic difference with that derived from ICP-OES (more than 189%), whereas these results after correcting the self-absorption improve, so that the percentage relative errors reduce to less than 2.8%; which proves that the effect of self-absorption phenomenon is much more than what one can initially think about. Here, it should be emphasized that the dramatic difference between the concentrations before and after self-absorption correction is mainly due to taking into account all of resonant and near-resonant calcium lines.

Fig. 6
figure 6

The calcium concentration of the five leaves calculated by the method: LIBS-IRS before (red bar) and after (blue bar) self-absorption correction; ICP-OES (green bar)

Full size image

Moreover, it must further be noted that a laser-induced plasma is generally both inhomogeneous and non-stationary. The nature of plasma inhomogeneity causes both the electron density and the plasma temperature to decrease with increasing distance not only from sample surface but also laterally relative to the symmetric plane of the plume. On the other hand, the plasma non-stationarity can give rise to a change of the above parameters in each point of the plasma by elapsing time. Hence, one can expect that LTE is deviated due to these two features, resulting in serious errors in the final results; but experimental outcomes indicate that this is not true in many cases. In more precise terms, in LIBS process, the results obtained from the conventional formulas are actually concerned with the time–space-averaged temperature, and they are often well compatible with the experimental amounts. From a general perspective, this means that, in the acquisition time of the emission spectrum (which is between 2 and 9 μs in our experiment), the plasma condition can averagely be supposed to be spatially homogeneous and temporally stationary.

In the end, it is essential to mention that the optimized delay time and gate width in LIBS process to fulfill LTE condition heavily depend on parameters such as the stimulating laser energy, pulse duration, ambient gas, ambient pressure, material, etc., which are used in the actual experiment. As far as our experiment concerned, the most important reason for fulfilling LTE condition is that the plasma temperature obtained from the line-pair ratio method and Boltzmann plot accomplishes us to the concentrations that are very close to those obtained from ICP method.

5 Conclusion

In this paper, qualitative and quantitative analyses of the leaf of five plants: fennel, bay leaf, dandelion, spinach, and parsley were scrutinized by the LIBS method. After measuring the plasma emission spectrum of each leaf, some (its) constituent elements including calcium were identified using the library database of NIST. Then, the plasma temperature and the plasma electron density were calculated by the BP (and also the LPR) method and the Saha–Boltzmann equation, respectively. In the next step, the optical penetration depth and the self-absorption coefficient of each spectral line were obtained using the peak intensity-based model. The non-self-absorbed spectral photon flux of each line, which is used in the conventional LIBS calculations to determine the concentration, was calculated by a recursive algorithm. From the plasma emission spectrum obtained from the LIBS experiment, eleven spectral lines of calcium as the analyte and three spectral lines of copper as the reference were identified and used for calculating the plasma temperature, the electron density, the concentrations, etc. The quantitative analysis was carried out through internal reference standard method, in both cases, with and without correcting the self-absorption effect. To obtain more accurate results, the plasma temperature, the electron density, \({\text{R}}\), and the calcium concentration in each specimen were calculated by the information obtained from the average of 25 spectra. The measurements indicate that, before correcting self-absorption effect, the percentage relative errors related to calcium concentration of the five leaves, fennel, bay leaf, dandelion, spinach, and parsley obtained from the method LIBS-IRS relative to ICP-OES are 189.21%, 282.43%, 190.10%, 249.05%, and 260.92%, while, after correcting self-absorption effect, they improved to the amounts of 0.69%, 0.30%, 0.56%, 2.76%, and 0.73%, respectively.