1 Introduction

One of the most important study subjects of the twenty-first century is to attempt to model nature with nonlinear phenomena [1,2,3,4,5,6,7,8,9,10,11,12,13]. The basic concepts of nonlinear science are that the whole is more than the sum of parts and systems wanders between chaotic and coherent structures. The most useful tool used by scientists for mathematically expressing of these phenomena is nonlinear differential equations [2, 14,15,16,17,18,19,20,21,22,23,24]. Nonlinear optics, which is the subject of the interaction of light with nonlinear media, is a good example of nonlinear science and has been studied extensively in recent years [25,26,27]. Due to its deep mathematics, it includes, nonlinear optics attracts the interest of mathematicians as well as physicists. Thanks to his theoretical work on superconductor physics, Vitali Ginzburg (1916–2009), winner of the Nobel Prize in 2003, is undoubtedly one of the most important scientists of the last century. Ginzburg, along with another Nobel Prize winner scientist Landau (1908–1968), developed the Ginzburg–Landau model for theoretically explaining the superconductivity mechanism. The cubic complex Ginzburg–Landau (CGLE) equation they suggested has been used not only to describe superconductivity, but also to explain many phenomena in a wide spectrum from superfluidity [28] to Bose–Einstein condensation [29], strings in field theory [30] to lasers [31]. The CGLE is a very general type of equation that governing a vast variety of bifurcations and nonlinear wave phenomena in spatiotemporally extended systems [32].

Due to the freeness of exchanging energies with an external source, the dissipative systems are more complicated than the Hamiltonian systems. CGLE is a powerful tool for investigation of the nonequilibrium dynamics of weakly nonlinear systems which are interacting with an external energy source. CGLE includes the gain, saturation, and nonlinear dispersion terms [33]. Therefore, it has been used to study many dissipative systems, although it has been proposed to explain superconductivity phenomenon [34].

On the other hand, a recent study by Horikiri et al. [35] has revealed the close relationship between superconductors, Bose–Einstein condensates, and lasers. This similarity is due to the fact that the quantum events of electrons at the microscopic level in the superconductors show their effects with a high synchronization at the macroscopic level. In the case of lasers, photons show a similar effect to form a single coherent light with a high synchronization. Bose–Einstein condensate atoms also have a similar effect when trapped in a single quantum state. In their experiment, Horikiri et al. observed a high-energy side-peak emission that cannot be explained by classical semiconductor laser phenomenon. According to the experimental data, this peak can be originated from the strong electron–hole pairings which are similar to BCS theory that is a special case of the Ginzburg–Landau equation near the critical phase transition state. Therefore, it is quite plausible that the superconductors, Bose–Einstein condensation, and lasers can be examined by CGLE.

In this study, the new solitary and traveling wave solutions of conformable time fractional [36, 37] CGLE are acquired with the aid of Jacobi elliptic expansion method. All the obtained solutions are new, and to the best of our knowledge, they are seen first in the literature. The rest of article is organized as follows. In Sect. 2, some literary review of the considered is expressed. In Sect. 3, the Jacobi elliptic function method is declared. In Sect. 4, the solutions for fractional complex Ginzburg–Landau equation are evaluated using Jacobi elliptic function method with the aid of computer software Mathematica. In Sect. 5, 2D and 3D graphical representations of the obtained solutions are given.

2 Governing equation

The 2D dimensions form of fractional complex Ginzburg–Landau equation, which is going to be considered in this study, is expressed as follows:

$$\begin{aligned} i D_t^{\mu }q+aq_{xx}+bG(|q|^2)q & = \frac{1}{|q|^2 q^*}\left[ \alpha |q|^2(|q|^2)_{xx}\right. \nonumber \\& \quad \left. -\beta \{(|q|^2)_x\}^2\right] +\gamma q, \end{aligned}$$
(1)

where q(x, t) is unknown function, \(\mu \in (0,1)\), x denotes the distance along the fibers, while t implies the time; \(a, b, \alpha , \beta\) and \(\gamma\) are constants. The coefficients a and b occur from the group velocity dispersion (GVD) and nonlinearity. The terms \(\alpha , \beta\) and \(\gamma\) occur from the perturbation effects; in particular, \(\gamma\) arises from the detuning effect. In Eq. (1), real-valued function G must hold the uniformity of the complex function \(G(|q|^2)q\) which is k times continuously differentiable, hence

$$\begin{aligned} G(|q|^2)q \in \bigcup _{m,n=l}^\infty C^k ((-n,n)\times (-m,m);\,R^2). \end{aligned}$$
(2)

To get the solution of Eq. (1), the usual decomposition into phase–amplitude components yields

$$q(x,t) = H(\xi )e^{{\left( { - \kappa x + \omega \frac{{t^{\mu } }}{\mu } + \theta } \right)}} ,$$
(3)

where the wave variable \(\xi\) is defined as

$$\begin{aligned} \xi =k\left( x-\nu \frac{t^\mu }{\mu }\right) . \end{aligned}$$
(4)

The function H implies the pulse shape, \(\nu\) denotes the speed of the soliton, \(\kappa\) symbolize the soliton frequency, \(\omega\) is the soliton wave number, and \(\theta\) is the phase constant. When the amplitude–phase decomposition subrogated into Eq. (1) and separating into real and imaginary parts, the following equations arise

$$\begin{aligned} -\omega H+a(k^2H_{\xi \xi }-\kappa ^2H)+bG(H^2)H & = 2k^2(\alpha -2\beta )\frac{(H_{\xi })^2}{H}\nonumber \\& \quad +2k^2\alpha H_{\xi \xi }+\gamma H \end{aligned}$$
(5)

and

$$\begin{aligned} \nu =-2a\kappa . \end{aligned}$$
(6)

By selecting

$$\begin{aligned} \alpha =2\beta \end{aligned}$$
(7)

the first term on the right-hand side of Eq. (5) zeroised. Thus, Eq. (1) turns to

$$\begin{aligned} i D_t^{\mu }+aq_{xx}+bG(|q|^2)q=\frac{\beta }{|q|^2 q^*}\left[ 2|q|^2(|q|^2)_{xx}-\{(|q|^2)_x\}^2\right] +\gamma q \end{aligned}$$
(8)

and Eq. (5) changes to

$$\begin{aligned} k^2(a-4\beta )H_{\xi \xi }-(\omega +a\kappa ^2+\gamma )H+bG(H^2)H=0. \end{aligned}$$
(9)

3 Brief description of the Jacobi elliptic function expansion method

In this part, basic principles of Jacobi elliptic function expansion method are expressed step by step.

Step 1:

Conceive the following nonlinear conformable time fractional equation:

$$\begin{aligned} F\left( u,\frac{\partial ^{\mu } u}{\partial t^{\mu } }, \frac{\partial u}{\partial x},\frac{\partial ^{2\mu } u}{\partial t^{2\mu } } ,\frac{\partial ^{2} u}{\partial x^{2} },\ldots \right) =0. \end{aligned}$$
(10)

Using the wave transformation, where w is the arbitrary constants to be determined later

$$\begin{aligned} u=u(\xi ),\,\xi =x+w\frac{t^{\mu }}{\mu } \end{aligned}$$
(11)

to Eq. (10), then employing the chain rule [37]

$$\begin{aligned} \frac{\partial ^{\mu }(.)}{\partial t^{\mu } }=m\frac{{\text{d}}(.)}{{\text{d}}\xi },\,\frac{\partial (.) }{\partial x}=n\frac{{\text{d}}(.)}{{\text{d}}\xi },\,\frac{\partial (.) }{\partial y}=s\frac{{\text{d}}(.)}{{\text{d}}\xi },\ldots \end{aligned}$$
(12)

yields an (ODE)

$$\begin{aligned} O(u,u',u'',u''', \ldots ), \end{aligned}$$
(13)

where prime indicates the integer order derivation with respect to variable \(\xi\).

Step 2:

Assume that the function \(u(\xi )\) can be recognized as sum of finite series:

$$\begin{aligned} u(\xi )= {\displaystyle \sum \limits _{i=0}^{s}} a_{i}F^{i}(\xi ), \end{aligned}$$
(14)

where \(F(\xi )\) is the solution of the following ODE:

$$\begin{aligned} (F^{\prime })^{2}(\xi )=PF^{4}(\xi )+QF^{2}(\xi )+R. \end{aligned}$$
(15)

In this differential equation, \(F'={\text{d}}F/{\text{d}}\xi\), \(\xi =\xi (x,t,y)\), and P, Q, R are constants can be chosen from Table 1. Equation (15) has the following solutions shown in Table 1, where \(i^{2}=-1\). The denoted functions in Table 1 are double periodic and called the Jacobian elliptic functions \(sn\xi = sn(\xi ;r), cn\xi = cn(\xi ;r)\) and \(dn\xi = dn(\xi ;r)\), where \(r(0<r<1)\) is the modulus of the elliptic function and satisfy the following features:

$$\begin{aligned}&sn^{2}\xi +cn^{2}\xi =1,\\&dn^{2}\xi +r^{2}sn^{2}\xi =1,\\&\frac{{\text{d}}}{{\text{d}}\xi }sn\xi =cn\xi dn\xi ,\\&\frac{{\text{d}}}{{\text{d}}\xi }cn\xi =-sn\xi dn\xi ,\\&\frac{{\text{d}}}{{\text{d}}\xi }dn\xi =-r^{2}cn\xi sn\xi . \end{aligned}$$

This method is based on using the advantage of the solutions of the auxiliary ODE (15) to construct abundant families of Jacobian elliptic solutions.

Table 1 Solutions table of Eq. (15) for chosen values of P, Q and R [38, 39]
Full size table

Since \(r\rightarrow 0\) ve \(r\rightarrow 1\), Jacobi elliptic functions transform to trigonometric and hyperbolic functions, as shown in Table 2; thus, we acquire the trigonometric function solutions and solitonic solutions of the regarded equation.

Step 3:

For the solution, the constants \(s,a_{i}(i=0,1,2,\ldots ,s)\) are going to be identified too. For this purpose, we can use balancing procedure. This procedure depends on balancing the highest order linear term:

$$\begin{aligned} O\left( \frac{{\text{d}}^{p}u}{{\text{d}}\xi ^{p}}\right) =s+p, \ \ \ \ p=0,1,2,\ldots \end{aligned}$$
(16)

and highest order nonlinear term:

$$\begin{aligned} O\left( u^{q}\frac{{\text{d}}^{p}u}{{\text{d}}\xi ^{p}}\right) =(q+1)s+p \ \ \ \ \ \ p=0,1,\ldots , \ \ \ \ \ \ q=0,1,\ldots . \end{aligned}$$
(17)

in (13). Hence, integer s in (14) can be examined. Substituting (14) and equating all the coefficients of F to zero, then nonlinear algebraic system arises for \(a_{i},(i=0,1,2,\ldots ,s)\). Computing the solution of the system with the aid of a Mathematica and utilizing all the values for P, Q, R (15) in Table 1, we can obtain the values for \(a_{i},(i=0,1,2,\ldots ,s)\) and w.

Step 3:

Finally, we can gather all the obtained results; hence, we can get exact solutions for Eq.(10).

4 Application to complex Ginzburg–Landau equation

Equation (19) will be considered with Kerr law nonlinearity. The Kerr law of nonlinearity comes from the fact that a light wave in an optical fiber encounters nonlinear responses from non-harmonic motion of electrons with an external electric field. \(G(u)=u\) is obtained from the Kerr law nonlinearity, so that Eq. (8) turns into

$$\begin{aligned} i D_t^{\mu }+aq_{xx}+b|q|^2q=\frac{\beta }{|q|^2 q^*}\left[ 2|q|^2(|q|^2)_{xx}-\{(|q|^2)_x\}^2\right] +\gamma q \end{aligned}$$
(18)

and Eq. (19) becomes

$$\begin{aligned} k^2(a-4\beta )H_{\xi \xi }-(\omega +a\kappa ^2+\gamma )H+bH^3=0. \end{aligned}$$
(19)

Using the balancing principle, we get \(s=1\). Hence, the solution of Eq.(19) can be expressed as

$$\begin{aligned} H(\xi )=a_{0}+a_{1}F(\xi ). \end{aligned}$$
(20)

Differentiating Eq.(20) twice led to

$$\begin{aligned} H_{\xi \xi }=a_{1}F''(\xi )+2a_{2}((F'(\xi ))^{2}+F(\xi )F''(\xi )) \end{aligned}$$
(21)

then by Eq. (15)

$$\begin{aligned} F''=2PF^{3}+QF. \end{aligned}$$
(22)

Placing (22) and (15) into (21) led to

$$\begin{aligned} H_{\xi \xi } & = a_{1}(2PF^{3}+QF)+2a_{2}(PF^{4}+QF^{2}+R)\nonumber \\& \quad +2a_{2}F(2PF^{3}+QF). \end{aligned}$$
(23)

Subrogating Eqs.(20) and (23) in Eq. (19) and regarding each coefficient of F to be zero lead the following equation system:

$$\begin{aligned}&a_0 (-a \kappa ^2-\gamma -\omega )+a_0^3 b=0,\nonumber \\&a_1 (-a \kappa ^2-\gamma -\omega )+a_1 k^2 Q (a-4 \beta )+3 a_0^2 a_1 b=0,\nonumber \\&3 a_0 a_1^2 b=0,\nonumber \\&2 a_1 k^2 P (a-4 \beta )+a_1^3 b=0. \end{aligned}$$
(24)

Solving the above system by the help of Mathematica, we get the following solution set:

$$\begin{aligned} a_0=0, a_1=\frac{i\sqrt{2P} \sqrt{a \kappa ^2+\gamma +\omega }}{ \sqrt{bQ}}, k=\frac{\sqrt{a \kappa ^2+\gamma +\omega }}{\sqrt{a Q-4 \beta Q}}. \end{aligned}$$

Finally, gathering the values together with Eq.(20), we can get exact solutions of Eq.(18) by choosing the suitable values from Tables 1 and 2 as follows.

Table 2 Jacobi elliptic functions for \(r\rightarrow\)0 and \(r\rightarrow\)1 [38, 39]
Full size table

When \(P=r^{2},\) \(Q=-(1+r^{2}),\) \(R=1\) are chosen, \(F={\text{ sn }}\) from Table 1, solution can be written as

$$\begin{aligned} q_{1}(x,t)= & {} \frac{ \sqrt{2} \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {sn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( -r^2-1\right) -4 \beta \left( -r^2-1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) },\\ q_{2}(x,t)= & {} \frac{ \sqrt{2} \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {cd} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( -r^2-1\right) -4 \beta \left( -r^2-1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Setting \(P=-r^{2},\) \(Q=2r^{2}-1,\) \(R=1-r^{2}\), from Table 1 \(F={\text{ cn }}\), the solution can be mentioned as

$$\begin{aligned} q_{3}(x,t)=\frac{ \sqrt{2} \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {cn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2 r^2-1\right) -4 \beta \left( 2 r^2-1\right) }}\right) }{\sqrt{b} \sqrt{2 r^2-1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Supposing \(P=-1,Q=2-r^{2},R=r^{2}-1\), from Table 1, so the solution can be obtained

$$\begin{aligned} q_{4}(x,t)=-\frac{\sqrt{2} \sqrt{a \kappa ^2+\gamma +\omega } \text {dn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2-r^2\right) -4 \beta \left( 2-r^2\right) }}\right) }{\sqrt{b} \sqrt{2-r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Supposing \(P=1,Q=-(1+r^{2}),R=r^{2}\), from Table 1, so the solution can be obtained:

$$\begin{aligned} q_{5}(x,t)= & {} \frac{ \sqrt{2} \sqrt{a \kappa ^2+\gamma +\omega } \text {ns} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( -r^2-1\right) -4 \beta \left( -r^2-1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) },\\ q_{6}(x,t)= & {} \frac{ \sqrt{2} \sqrt{a \kappa ^2+\gamma +\omega } \text {dc} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( -r^2-1\right) -4 \beta \left( -r^2-1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Supposing \(P=1-r^2,Q=2r^2-1,R=-r^{2}\), from Table 1, so the solution can be obtained

$$\begin{aligned} q_{7}(x,t)=\frac{ \sqrt{2} \sqrt{r^2-1} \sqrt{a \kappa ^2+\gamma +\omega } \text {nc} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2 r^2-1\right) -4 \beta \left( 2 r^2-1\right) }}\right) }{\sqrt{b} \sqrt{2 r^2-1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Supposing \(P=r^2-1,Q=2-r^2,R=-1\), from Table 1, so the solution can be obtained:

$$\begin{aligned} q_{8}(x,t)=\frac{ \sqrt{2} \sqrt{1-r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {nd} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2-r^2\right) -4 \beta \left( 2-r^2\right) }}\right) }{\sqrt{b} \sqrt{2-r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=1-r^2,\) \(Q=2-r^{2},\) \(R=1\), then the solution arises as follows:

$$\begin{aligned} q_{9}(x,t)=\frac{ \sqrt{2} \sqrt{-1+r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {sc} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2-r^2\right) -4 \beta \left( 2-r^2\right) }}\right) }{\sqrt{b} \sqrt{2-r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=-r^2(1-r^2),\) \(Q=2r^{2}-1,\) \(R=1\), then the solution can be examined:

$$\begin{aligned} q_{10}(x,t)=\frac{ \sqrt{2} \sqrt{r^2 \left( 1-r^2\right) } \sqrt{a \kappa ^2+\gamma +\omega } \text {sd} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2 r^2-1\right) -4 \beta \left( 2 r^2-1\right) }}\right) }{\sqrt{b} \sqrt{2 r^2-1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=1,\) \(Q=2-r^{2},\) \(R=1-r^2\), then the solution acquired as

$$\begin{aligned} q_{11}(x,t)=\frac{ \sqrt{2} \sqrt{a \kappa ^2+\gamma +\omega } \text {cs} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2-r^2\right) -4 \beta \left( 2-r^2\right) }}\right) }{\sqrt{b} \sqrt{r^2-2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=1,\) \(Q=2r^{2}-1,\) \(R=-r^2(1-r^2)\), then the solution can be established as

$$\begin{aligned} q_{12}(x,t)=\frac{ \sqrt{2} \sqrt{a \kappa ^2+\gamma +\omega } \text {ds} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{a \left( 2 r^2-1\right) -4 \beta \left( 2 r^2-1\right) }}\right) }{\sqrt{b} \sqrt{1-2 r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Regarding \(P=-\frac{1}{4},Q=\frac{r^2+1}{2},\) \(R=-\frac{(1-r^2)^2}{4}\) and \(F=r cn\pm dn\) from Table 1, the solution can be evaluated as

$$\begin{aligned} q_{13,14}(x,t)=-\frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \pm \text {dn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) +r \text {cn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) \right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Regarding P, Q , R as \(P=\frac{1}{4},Q=\frac{-2r^2+1}{2},\) \(R=\frac{1}{4}\), hence, the solution is constructed

$$\begin{aligned} q_{15,16}(x,t)=\frac{ \sqrt{a \kappa ^2+\gamma +\omega } \left( \text {ns} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) \mp \text {cs}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) \right) }{\sqrt{b} \sqrt{2 r^2-1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Setting \(P=\frac{1-r^2}{4},Q=\frac{r^{2}+1}{2},R=\frac{1-r^2}{4}\) from Table 1 \(F=\hbox {nc}\mp \hbox {sc}\), due to this settings the solution can be expressed as

$$\begin{aligned} q_{17,18}(x,t)=\frac{ \sqrt{r^2-1} \sqrt{a \kappa ^2+\gamma +\omega } \left( \text {nc} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) \mp \text {sc}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) \right) }{\sqrt{b} \sqrt{r^2+1}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Setting \(P=\frac{1}{4},Q=\frac{r^{2}-2}{2},R=\frac{r^4}{4}\) from Table 1 \(F=\hbox {ns}\mp \hbox {ds}\), due to this settings the solution can be expressed as

$$\begin{aligned} q_{19,20}(x,t)=\frac{ \sqrt{a \kappa ^2+\gamma +\omega } \left( \text {ns} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) \mp \text {ds}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) \right) }{\sqrt{b} \sqrt{2-r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Assigning \(P=\frac{r^{2}}{4},Q=\frac{r^{2}-2}{2},R=\frac{r^{2}}{4}\), this assignments corresponds to the solution:

$$\begin{aligned} q_{21,22}(x,t)=\frac{ \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \left( i\text {sn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) \mp \text {cn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) \right) }{\sqrt{b} \sqrt{r^2-2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Assigning \(P=\frac{r^{2}}{4},Q=\frac{r^{2}-2}{2},R=\frac{r^{2}}{4}\), the solution determined as

$$\begin{aligned} q_{23,24}(x,t)=\frac{ \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {dn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) }{\sqrt{b} \sqrt{2-r^2} \left( \mp \text {cn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) +\sqrt{1-r^2} \text {sn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) \right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Choosing \(P=\frac{1}{4},Q=\frac{1-2r^2}{2},R=\frac{1}{4}\), the solution is constructed as

$$\begin{aligned} q_{25,26}(x,t)= & {} \frac{ \sqrt{a \kappa ^2+\gamma +\omega } \left( i r \text {cn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) \mp \text {dn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) \right) }{\sqrt{b} \sqrt{1-2 r^2}}e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Choosing \(P=\frac{1}{4},Q=\frac{1-2r^2}{2},R=\frac{1}{4}\) from Table 1, this choices follows \(F=\frac{sn}{1\pm cn}\), so that the solution can be constructed as

$$\begin{aligned} q_{27,28}(x,t)=\frac{ \sqrt{a \kappa ^2+\gamma +\omega } \text {sn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) }{\sqrt{b} \sqrt{2 r^2-1} \left( \pm \text {cn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( 1-2 r^2\right) -2 \beta \left( 1-2 r^2\right) }}\right) +1\right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

Supposing \(P=\frac{r^2}{4},Q=\frac{r^2-2}{2},R=\frac{1}{4}\), from Table 1, this choices correspond to \(F=\frac{sn}{1\pm dn}\), so solution can be stated as

$$\begin{aligned} q_{29,30}(x,t)=\frac{ \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {sn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) }{\sqrt{b} \sqrt{r^2-2} \left( \pm \text {dn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( 2-r^2\right) }}\right) +1\right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=\frac{r^{2}-1}{4},\,Q=\frac{r^{2}+1}{2},\,R=\frac{r^{2}-1}{4}\,\), then the solution is declared as

$$\begin{aligned} q_{31,32}(x,t)=\frac{ \sqrt{1-r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {dn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1} \left( \mp r\text {sn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) +1\right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

While \(P=\frac{1-r^{2}}{4},\,Q=\frac{r^{2}+1}{2},\,R=\frac{1-r^{2}}{4}\,\), then the solution informed as

$$\begin{aligned} q_{33,34}(x,t)=\frac{ \sqrt{r^2-1} \sqrt{a \kappa ^2+\gamma +\omega } \text {cn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1} \left( \mp \text {sn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) +1\right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

When P, Q, R are set as \(P=\frac{(1-r^{2})^2}{4},Q=\frac{r^{2}+1}{2},R=\frac{1}{4}\), so the solution is settled as

$$\begin{aligned} q_{35,36}(x,t)=\frac{i \sqrt{\left( 1-r^2\right) ^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {sn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) }{\sqrt{b} \sqrt{r^2+1} \left( \text {dn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) \mp \text {cn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2+1\right) -2 \beta \left( r^2+1\right) }}\right) \right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

When P, Q, R are set as \(P=\frac{(r^{2})}{4},Q=\frac{r^{2}-2}{2},R=\frac{1}{4}\), so the solution can demonstrated as

$$\begin{aligned} q_{37,38}(x,t)=\frac{ \sqrt{r^2} \sqrt{a \kappa ^2+\gamma +\omega } \text {cn} \left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( r^2-2\right) }}\right) }{\sqrt{b} \sqrt{r^2-2} \left( \mp \text {dn}\left( \frac{\sqrt{a \kappa ^2+\gamma +\omega } \left( \frac{2 a \kappa t^{\mu }}{\mu }+x\right) }{\sqrt{\frac{1}{2} a \left( r^2-2\right) -2 \beta \left( 2-r^2\right) }}\right) +\sqrt{1-r^2}\right) }e^{i \left( \theta +\frac{\omega t^{\mu }}{\mu }-\kappa x\right) }. \end{aligned}$$

5 Graphical representations

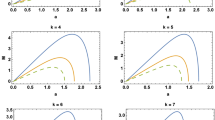
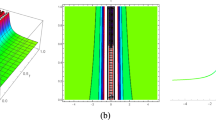
Some of the graphical representations of remarkable solutions has been shown in this section. 2D-dimensional graphical illustrations are given to compare the behavior of the solutions for different values of parameters. In addition, 3D surface graphics are represented to show the spatiotemporal extension of the obtained wave solutions. Surface plots for real and imaginary parts of the solution \(q_1(x,t)\) are shown in Fig. 1a, b, respectively. It can be seen that the amplitude of the waves is increased with imaginary and real spatial propagation. To examine the dependence of the wave function on parameters, 2D graphs are given for the different values of the parameters beta and a in Fig. 1c–f, respectively, for the same solution. As can be seen both for Fig. 1c, d that increasing \(\beta\) caused to decrease in amplitude of real and imaginary parts. On the other hand, increase in the amplitude of the wave function and an accompanying phase shift of \(\pi /2\) for the increasing values of the parameter a can be seen in Fig. 1e, f. It can be thought that these types of phase shifts can cause to decaying of the optical pulses (Fig. 2).

Fig. 1
figure 1

Surface plots of \(q_1(x,t)\) for \(\theta =0.8,\kappa =2,r=1,b=0.1,\mu =0.75,\omega =-1,\gamma =0.1\)

Full size image
Fig. 2
figure 2

Surface plots of \(q_1(x,t)\) for \(\beta =1, a=0.2, t=1, \theta =0.8,\kappa =2,r=1,b=0.1,\mu =0.75,\omega =-1,\gamma =0.1\) and different values of \(\mu\)

Full size image

Surface plots for real and imaginary parts of the solution \(q_2(x,t)\) are shown in Fig. 3a, b, respectively. As can be seen from the figure that obtained result is a soliton solution. As can be seen both for Fig. 3c, d that increasing \(\gamma\) caused to increase in the amplitude of real and imaginary parts. On the other hand, increase in the amplitude of the wave function and an accompanying slight phase shift for the increasing values of the parameter \(\gamma\) can be seen in Figs. 3c, d and 4.

Fig. 3
figure 3

Surface plots of \(q_2(x,t)\) for \(\theta =1,\beta =0.001, \kappa =1,r=1,a=0.2, b=0.1,\mu =0.8,\omega =0.1\)

Full size image
Fig. 4
figure 4

Surface plots of \(q_2(x,t)\) for \(t=1, \gamma =1, \theta =1,\beta =0.001, \kappa =1,r=1,a=0.2, b=0.1,\mu =0.8,\omega =0.1\) and different values of \(\mu\)

Full size image

6 Conclusions

In this article, authors acquired the wave solutions of conformable fractional complex Ginzburg–Landau equation arising in nonlinear optics using Jacobi elliptic expansion method. The Jacobi elliptic function method includes the most general form of the solutions, because the method includes Jacobi elliptic function. The limits of the Jacobi elliptic functions give both periodic, trigonometric, hyperbolic, etc. solutions of the considered equation. The obtained results show that considered method is efficient, accurate, and reliable tool to solve the nonlinear fractional partial differential equations in conformable sense. In addition, 3D graphical illustrations and 2D comparative graphics for different values of various parameters are represented to see the effects of the changing values of parameters over the solution. This study will illuminate the researchers for further studies who make researches on optics and laser technology.