Paraxial propagation of radially polarized first-order chirped Airy Guassian beams in uniaxial crystals orthogonal to the optical axis

Abstract

We have studied the propagation of radially polarized first-order chirped Airy Guassian beams (RPCAiGBs) in uniaxial crystals orthogonal to the optical axis. The intensity distribution, the maximum intensity, the propagation trajectory and velocity of the beams in different view planes are investigated in this paper. We find that for the x component (RPCAiGXBs) and the y component (RPCAiGYBs) of the RPCAiGBs, the intensity first propagates along the x and y directions, respectively. Later, the intensity of these two components flows into the side lobes along the x direction. We also examine the effects on the trajectory, the velocity and the focused performance of the RPCAiGBs caused by the distribution factor ($\chi _0$), the first-order chirp parameter ($\beta$) and the ratio of the extraordinary refractive index ($n_\mathrm{e}$) to the ordinary refractive index ($n_\mathrm{o}$) ($n_\mathrm{e}/n_\mathrm{o}$). Thus, by choosing appropriate $\chi _0$, $n_\mathrm{e}/n_\mathrm{o}$ and $\beta$, we are able to adjust these characteristics.

1 Introduction

In 1979, the Airy beams were proven theoretically as a solution of force-free Schrödinger equation in quantum physics by Berry and Balazs [1]. It has been proven that under adverse environments such as in scattering and turbulent media, the Airy beams are robust, which shows a self-healing property [2]. Also there is a self-accelerating feature even in the absence of any external potential [3, 4]. The Airy beams contain infinite energy which is not physically realizable. However, in 2007, Airy beams with finite energy were demonstrated experimentally by Siviloglou et al. [3, 4]. Subsequently, with the unique features of self-healing, self-accelerating and nondiffraction [5], the Airy beams have drawn much attention and have been investigated widely.

Owing to their novel characteristics [6, 7], the radially polarized beams (RPBs) have aroused much attention and have been studied in many fields, for instance, acceleration techniques [8, 9], particles guiding or trapping [10, 11], high resolution microscopy [12] and particularly material processing [13, 14]. In 2006 and 2007, the radially polarized light beams [15, 16] and radially polarized elegant light beams [17] were investigated by Deng et al. Later, in 2016, the RPBs were further studied by Gu et al. [18] who investigated vectorial self-diffraction behaviors and polarization evolution properties of the RPBs induced by anisotropic Kerr nonlinearity. Then, Khonina et al. developed the way to generate the radially and azimuthally polarized beams, including the beams of higher orders [19]. Recently, in 2018, the radially polarized Airy beams with unique factors like vortex and chirp have been studied by Zhong et al. [20] and Xie et al. [21].

The first-order chirped Airy Guassian beams are obtained from the Airy beams multiplied by a Guassian factor and including a first-order chirp parameter. On the one hand, the Airy Gaussian beams (AiGBs) make the Airy beams propagate in a more realistic way since the AiGBs carry finite power, retain the diffraction-free property within a limited propagation distance, and can be realized experimentally to a very good approximation [22]. On the other hand, a chirp is a signal where the frequency increases or decreases with time. In the early 1990s, the first demonstration of controlling and using simple linear chirped laser pulses was carried by Melinger et al. [23]. Later, Zhang et al. studied the impacts of a linear chirp and a quadratic chirp on finite energy Airy beams in a linear medium with an external parabolic potential [24]. Recently, the propagation properties of the chirped Airy beams through the gradient-index medium [25] and the chirped Airy vortex beams through left-handed and right-handed material slabs [26] have been discussed, respectively.

It is interesting to investigate the propagation of laser beams through uniaxial crystals owing to their important applications in the conversion of polarization [27], amplitude and phase modulation [28, 29], and so on. The propagation properties of the Airy beams [30], the circular Airy beams [31, 32], the Airy vortex beams [33], the Airy Gaussian beams [34, 35], the Airy Guassian vortex beams [36, 37], the chirped Airy vortex beams [38], the chirped Airy Guassian vortex beams [39] and the radially polarized Airy beams [21] through uniaxial crystals have been discussed. However, there is no report on the paraxial propagation of the radially polarized first-order chirped Airy Guassian beams (RPCAiGBs) in uniaxial crystals. Thus, in the rest of this paper, we will discuss the RPCAiGBs in uniaxial crystals propagating orthogonally to the optical axis.

The organization of the paper is as follows. In Sect. 2, analytical expressions, including the electric fields, propagation trajectories and the velocities of the x component (RPCAiGXBs) and y component (RPCAiGYBs) of the RPCAiGBs in such medium will be deduced. In Sect. 3, we will illustrate the propagating properties of the RPCAiGXBs and the RPCAiGYBs. Then, the impacts of the distribution factor ($\chi _0$), the first-order chirp factor ($\beta$) and the ratio of the extraordinary refractive index to the ordinary refractive index ($n_\mathrm{e}/n_\mathrm{o}$) will be discussed, separately. Finally, we conclude the results in Sect. 4.

2 Analytical expressions of the RPCAiGBs in uniaxial crystals orthogonal to the optical axis

In the Cartesian coordinate system, the z-axis is taken to be the propagation axis while the x-axis is chosen as the optical axis of the uniaxial crystal. The relative dielectric tensor $\varepsilon$ of the uniaxial crystal [29, 30, 40] is depicted as:

$$\begin{aligned} \varepsilon = \begin{pmatrix} n_e^{2} &{} 0 &{} 0 \\ 0 &{} n_o^{2} &{} 0 \\ 0 &{} 0 &{} n_o^{2} \end{pmatrix}, \end{aligned}$$

(1)

where $n_\mathrm{e}$ and $n_\mathrm{o}$ are the extraordinary and the ordinary refractive indices of the uniaxial crystal. Additionally, we suppose that the RPCAiGBs in the uniaxial crystal orthogonal to the optical axis is incident on the uniaxial crystals at the initial plane z = 0 where the electric fields can be expressed as:

$$\begin{aligned} E_x(x,y,0)= & {} \frac{x}{w_1}Ai\left( \frac{x}{w_1}\right) Ai\left( \frac{y}{w_2}\right) \,\mathrm{exp}\left[ \frac{ax}{w_1}+\frac{by}{w_2}+i\beta (\frac{x}{w_1}+\frac{y}{w_2})\right] \mathrm{exp}\left( -\frac{x^{2}+y^{2}}{w_0^{2}}\right) , \end{aligned}$$

(2)

$$\begin{aligned} E_y(x,y,0)= & {} \frac{y}{w_2}Ai\left( \frac{x}{w_1}\right) Ai\left( \frac{y}{w_2}\right) \,\mathrm{exp}\left[ \frac{ax}{w_1}+\frac{by}{w_2}+i\beta (\frac{x}{w_1}+\frac{y}{w_2})\right] \mathrm{exp}\left( -\frac{x^{2}+y^{2}}{w_0^{2}}\right) , \end{aligned}$$

(3)

where Ai($\cdot$) denotes the Airy function, a and b are exponential truncation factors ranging from 0 to 1 and $\beta$ stands for the first-order chirp factor. $w_0$ depicts the waist size of the initial beams and $w_1$, $w_2$ represent arbitrary transverse scales, for which $w_1=w_2=\chi _0w_0$, $\chi _0$ being the distribution factor displaying unique properties. If $\chi _0$ goes to 0, the RPCAiGBs will tend to be radially polarized first-order chirped Airy beams (RPCAiBs) and radially polarized first-order chirped Guassian beams (RPCGBs), if $\chi _0$ goes to infinity. Under paraxial approximation, the propagation of the RPCAiGBs in uniaxial crystal propagating orthogonally to the optical axis [29, 30] reads

$$\begin{aligned} E_x(x,y,z)= & {} \frac{ikn_0}{2\pi z}\mathrm{exp}(-ikn_ez)\iint _{-\infty }^{+\infty }U_1 \mathrm{d}x_0\mathrm{d}y_0, \nonumber \\ U_1= & {} E_x(x_0,y_0,0)\,\mathrm{exp}\begin{bmatrix} {-\frac{ik[n_o^{2}(x-x_0)^{^{2}}+n_e^{2}(y-y_0)^{2}]}{2zn_e}} \end{bmatrix}, \end{aligned}$$

(4)

$$\begin{aligned} E_y(x,y,z)= & {} \frac{ikn_0}{2\pi z}\mathrm{exp}(-ikn_oz)\iint _{-\infty }^{+\infty } U_2 \mathrm{d}x_0\mathrm{d}y_0, \nonumber \\ U_2= & {} E_y(x_0,y_0,0)\,\mathrm{exp} \begin{bmatrix} -\frac{ikn_o[(x-x_0)^{2}+(y-y_0)^{2}]}{2z} \end{bmatrix}, \end{aligned}$$

(5)

where z signifies the propagation distance and $k=2\pi /\lambda$ is the wave number, of which $\lambda$ represents the optical wavelength. After substituting Eqs. (2–3) into Eqs. (4–5), the propagation of the RPCAiGBs through the uniaxial crystal propagating orthogonally to the optical axis in a distance z can be deduced as:

$$\begin{aligned} E_x(x,y,z)= & {} \frac{ikn_o}{2zw_1}\frac{1}{\sqrt{P_1P_2}}\,\mathrm{exp}[S_1(x,y,z)]K_1K_2, \end{aligned}$$

(6)

$$\begin{aligned} E_y(x,y,z)= & {} \frac{ikn_o}{2zw_2}\frac{1}{P_3}\,\mathrm{exp}[S_2(x,y,z)]K_3K_4, \end{aligned}$$

(7)

where

$$\begin{aligned} \begin{aligned} S_1&=-ik\left( n_ez+\frac{n_0^{2}x^{2}+n_e^{2}y^{2}}{2zn_e}\right) -\frac{1}{4}\left( \frac{Q_1^{2}}{P_1}+\frac{Q_2^{2}}{P_2}\right) \\&+\frac{1}{8}\left( \frac{Q_1}{w_1^{3}P_1^{2}}+\frac{Q_2}{w_2^{3}P_2^{2}}\right) -\frac{1}{96}\left( \frac{1}{w_1^{6}P_1^{3}}+\frac{1}{w_2^{6}P_2^{3}}\right) , \\ S_2&=-ikn_oz-\frac{ikn_o(x^{2}+y^{2})}{2z}-\frac{1}{4P_3}(Q_3^{2}+Q_4^{2})\\&+\frac{1}{8P_3^{2}}\left( \frac{Q_3}{w_1^{3}}+\frac{Q_4}{w_2^{3}}\right) -\frac{1}{96P_3^{3}}(\frac{1}{w_1^{6}}+\frac{1}{w_2^{6}}), \\ K_1&=\left( -\frac{Q_1}{2P_1}+\frac{1}{8w_1^{3}P_1^{2}}\right) Ai(M_1)-\frac{1}{2w_1P_1}Ai'(M_1), K_2=Ai(M_2), \\ K_3&=\left( -\frac{Q_4}{2P_3}+\frac{1}{8w_2^{3}P_3^{2}}\right) Ai(N_1)-\frac{1}{2w_2P_3}Ai'(N_1), K_4=Ai(N_2), \\ M_1&=\frac{1}{16w_1^{4}P_1^{2}}-\frac{Q_1}{2w_1P_1}, M_2=\frac{1}{16w_2^{4}P_2^{2}}-\frac{Q_2}{2w_2P_2}, \\ N_1&=\frac{1}{16w_2^{4}P_3^{2}}-\frac{Q_4}{2w_2P_3}, N_2=\frac{1}{16w_1^{4}P_3^{2}}-\frac{Q_3}{2w_1P_3}, \\ P_1&=-\frac{1}{w_0^{2}}-\frac{ikn_o^{2}}{2zn_e}, P_2=-\frac{1}{w_0^{2}}-\frac{ikn_e}{2z}, P_3=-\frac{1}{w_0^{2}}-\frac{ikn_o}{2z}, \\ Q_1&=\frac{a+i\beta }{w_1}+\frac{ikn_0^{2}x}{zn_e}, Q_2=\frac{b+i\beta }{w_2}+\frac{ikn_ey}{z}, \\ Q_3&=\frac{a+i\beta }{w_1}+\frac{ikn_0x}{z}, Q_4=\frac{b+i\beta }{w_2}+\frac{ikn_oy}{z}. \end{aligned} \end{aligned}$$

(8)

$Ai'\left( \cdot \right)$ represents the derivative of the Airy function. Equations (6–7) suggest that the RPCAiGXBs are affected by both $n_\mathrm{e}$ and $n_\mathrm{o}$. Conversely, the RPCAiGYBs are only impacted by $n_\mathrm{o}$. Furthermore, the intensity of the RPCAiGXBs and the RPCAiGYBs in uniaxial crystals orthogonal to the optical axis can be described, respectively, as:

$$\begin{aligned} I_x=\left| E_x(x,y,z) \right| ^{2}, I_y=\left| E_y(x,y,z) \right| ^{2}. \end{aligned}$$

(9)

The total intensity of the RPCAiGBs in uniaxial crystals orthogonal to the optical axis is given by:

$$\begin{aligned} I=I_x+I_y. \end{aligned}$$

(10)

Next, the propagation trajectory expressions of the RPCAiGXBs on the x–z plane and y–z plane can be obtained from Eq. (6), which are

$$\begin{aligned} x_1=\frac{z^{2}n_{e}^{2}w_0^{4}}{4w_1^{3}(A^{2}+B_1^{2})}-\frac{\beta zn_{e}}{kn_{o}^{2}w_1}, y_1=\frac{z^{2}n_{e}^{2}w_0^{4}}{4w_2^{3}(A^{2}+B_2^{2})}-\frac{\beta z}{kn_{e}w_{2}}, \end{aligned}$$

(11)

and the velocity of the beams in the x and y directions can be described as:

$$\begin{aligned} V_{x1}= & {} \frac{zn_{e}^{2}w_{0}^{4}(A^{2}+B_{1}^{2})-zn_{e}^{2}w_{0}^{4}A^{2}}{2w_{1}^{3}(A^{2}+B_{1}^{2})^{2}}-\frac{\beta n_e}{kn_{o}^{2}w_{1}}, \end{aligned}$$

(12)

$$\begin{aligned} V_{y1}= & {} \frac{n_{e}w_{0}^{4}A(A^{2}+B_{2}^{2})-2zn_{e}^{2}w_{0}^{4}A^{2}}{4w_{2}^{3}(A^{2}+B_{2}^{2})^{2}}-\frac{\beta }{kn_{e}w_{2}}, \end{aligned}$$

(13)

where

$$\begin{aligned} A=2zn_e, B_1=kn_o^{2}w_0^{2}, B_2=kn_e^{2}w_0^{2}. \end{aligned}$$

(14)

Likewise, the propagation trajectory expressions of the RPCAiGYBs in x–z plane and y–z plane can be obtained from Eq. (7), which are

$$\begin{aligned} x_2=\frac{z^{2}w_0^{4}}{4w_1^{3}(C^{2}+D^{2})}-\frac{\beta z}{kn_ow_1}, y_2=\frac{z^{2}w_0^{4}}{4w_2^{3}(C^{2}+D^{2})}-\frac{\beta z}{kn_ow_2}, \end{aligned}$$

(15)

and the velocity of the beams in the x and y directions can be described as:

$$\begin{aligned} V_{x2}= & {} \frac{zw_{0}^{4}(C^{2}+D^{2})-zw_{0}^{4}C^{2}}{2w_{1}^{3}(C^{2}+D^{2})^{2}}-\frac{\beta }{kn_{o}w_{1}}, \end{aligned}$$

(16)

$$\begin{aligned} V_{y2}= & {} \frac{zw_{0}^{4}(C^{2}+D^{2})-zw_{0}^{4}C^{2}}{2w_{2}^{3}(C^{2}+D^{2})^{2}}-\frac{\beta }{kn_{o}w_{2}}, \end{aligned}$$

(17)

where

$$\begin{aligned} C=2z, D=kn_ow_o^{2}. \end{aligned}$$

(18)

3 Analysis and discussion

Having obtained Eqs. (6–7) and Eqs. (11–18) which indicate the analytical expressions of the electric field of the RPCAiGBs, their transverse trajectories and the velocity of the main lobes, we further investigate how the distribution factor, the first-order chirp parameter as well as the ratio of the extraordinary refractive index to the ordinary refractive index affect the propagation of the RPCAiGBs propagating uniaxial crystals orthogonally to the optical axis. The basic parameters are as follows: $\lambda =632$ nm, $w_1=w_2=100\mu$m, $a=b=0.1$, $n_\mathrm{o}=2.616$ and $Z_\mathrm{r}=kw_1^{2}/2$ (the Rayleigh range). Hereafter, these parameters are the same as those aforesaid. In this section, we treat $\chi _0$ as an argument whose value is changed during the discussion. Thus, the value of $w_0$ can be calculated by $w_1$, $w_2$ and $\chi _0$.

Firstly, we study the properties of the RPCAiGXBs in a number of different aspects. Figures 1a1, a2 are the intensity distributions of the RPCAiGXBs on z–x plane and z–y plane. Two conclusions we can get from these graphs: (1) the acceleration in the x direction is much faster than the one in the y direction; (2) there is a focused performance at Z = 15Z_r which corresponds to the highlighted point in Fig. 1a3. Figure 1a3 depicts the maximum intensity of the RPCAiGXBs as a function of propagating distance and Fig. 1b1–b4 depict the intensity distribution of the RPCAiGXBs on the x–y plane. Combining Fig. 1a3, b1–b4, one can see that as the propagation distance increases, the intensity in side lobes gradually flows into the main lobe along the x direction, and at the beginning, the maximum intensity keeps decreasing because focusing is weaker than diffraction. When Z > 10Z_r, as focusing gets stronger, the maximum intensity increases and the intensity continues converging into the main lobe forming a peak at Z = 15Z_r. Afterwards, the intensity flows back into the side lobes along the x direction and the intensity declines with propagating.

Fig. 1

Intensity distributions of the RPCAiGXBs propagating uniaxial crystals orthogonally to the optical axis with $\beta = 0.5$, $n_e=1.5n_o$ and $\chi _0 =0.1$. a1–a2 Intensity distribution on the z–x and z–y planes; a3 the maximum intensity as a function of z; b1–b4 Intensity distribution on x–y plane at Z = 1Z_rZ = 11Z_r, Z = 15Z_r and Z = 30Z_r, respectively

Fig. 2

Intensity distribution of the RPCAiGYBs through uniaxial crystals orthogonal to the optical axis with $n_\mathrm{e}=1.5n_\mathrm{o}$, $\beta =0.5$ and $\chi _0=0.1$. All are the same as those in Fig. 1 except for the view planes in Fig. 2b1–b4, where we set $z=1\mathrm{Z}_\mathrm{r}$, $z=10{\mathrm{Z}_\mathrm{r}}$, $z=20{\mathrm{Z}_\mathrm{r}}$ and $z=30{\mathrm{Z}_\mathrm{r}}$, respectively

Next, we investigate the propagation properties of the RPCAiGYBs when most of the parameter settings are the same as those in Fig. 1. Referring to the Eq. (15), we can find that the propagation trajectory of the RPCAiGYBs is the same both in the x and y directions as depicted in Fig.2a1–a2 if $w_1$ is equal to $w_2$. From Fig. 2a3, we see that the maximum intensity of the RPCAiGYBs decreases monotonically and there is no focused performance in the RPCAiGYBs when the parameters are identical to those in Fig. 1. Interestingly, in Fig. 2b1–b4, the intensity of the RPCAiGYBs flows along the y direction at first and converges into the main lobe gradually. However, after a certain distance, it transfers back into the side lobes along the x direction.

Now, we start to explore the effects of $\chi _0$, $\beta$ and $n_\mathrm{e}/n_\mathrm{o}$. First of all, we plot the propagation trajectories of the RPCAiGXBs and the RPCAiGYBs in Fig. 3a1–a3 and their corresponding velocities of the main lobes in Fig. 3b1–b3. Notably, as the trajectory expressions of the RPCAiGYBs in the x and y directions are the same, Fig. 3a3, b3 can be applied in both the x and y directions. For both the x component and the y component, the deflection degree gets larger when $\chi _0$ is smaller. By comparing Fig. 3a1, a3, one can see that the deflection of the RPCAiGXBs in the x direction is stronger than that of the RPCAiGYBs, while the deviation of the RPCAiGXBs in the y direction is weaker than that of the RPCAiGYBs. As for the acceleration of the RPCAiGXBs and the RPCAiGYBs as shown in Fig. 3b1–b3, it is clear that for these two components, the acceleration is larger as the $\chi _0$ gets smaller. Whereas, if it is set at a larger value like 0.3, the acceleration will first ascend and then decrease.

Fig. 3

The propagation trajectories of the RPCAiGXBs (a1–a2) and the RPCAiGYBs (a3) in the x and y directions and their corresponding velocity of the main lobes (b1–b3) when $\beta =0.5$ and $n_\mathrm{e}=1.5n_\mathrm{o}$

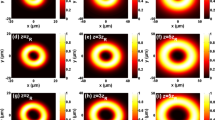
Figure 4 depicts the intensity distribution of the RPCAiGBs through uniaxial crystals orthogonal to the optical axis with different $\chi _0$ on x–y plane. One can see that when $\chi _0$ is taken to be 0.01, there are more side lobes and the process of intensity flowing along the x and y directions is more evident. However, when $\chi _0$ is set to the value 0.5, there is a lobe at first and four lobes at the end. So, it is seen that when $\chi _0$ is smaller [see Fig. 4a1], the RPCAiGBs tend to be the RPCAiBs and as $\chi _0$ getting larger, the characteristics of Airy beam become weaker. In other words, when $\chi _0$ is equal to 0.5, the RPCAiGBs act more like the RPCGBs [see Fig. 4c1]. Additionally, when $\chi _0$ is small, as we can see from the first two rows, the intensity is distributed along the x and y directions initially and these two directions stand for the RPCAiGXBs and the RPCAiGYBs, respectively. Gradually, it converges into the main lobes along the x and y directions. After a certain distance, the intensity of the beams flows into the side lobes in the x direction and that process is more evident and dominant for the RPCAiGYBs.

Fig. 4

Intensity distribution of the RPCAiGBs through uniaxial crystals orthogonal to the optical axis on x–y plane when $\chi _0$ is equal to 0.01 in (a1–a4), 0.1 in (b1–b4) and 0.5 in (c1–c4), respectively, when $\beta =0.5$ and $n_\mathrm{e}=1.5n_\mathrm{o}$

Fig. 5

The maximum intensity of the RPCAiGXBs (a1) and the RPCAiGYBs (a2) in uniaxial crystals orthogonal to the optical axis as a function of propagating distance with different $\chi _0$ in the case of $\beta =0.5$ and $n_\mathrm{e}=1.5n_\mathrm{o}$

Figure 5 plots the maximum intensity of the RPCAiGXBs and the RPCAiGYBs as a function of z for different $\chi _0$. There are some similarities for these two beams. For example, when $\chi _0$ is small, the maximum intensity first decreases because diffraction is more powerful than focusing; whereas after a certain distance, it increases owing to the fact that focusing surpasses diffraction. After arriving at the peak value, the maximum intensity drops gradually. In addition, it is seen that the maximum intensity gets larger and the focused position is farther away from the initial plane as $\chi _0$ gets smaller. However, if $\chi _0$ exceeds a certain value, the focused performance will disappear. Conversely, by comparing Fig. 5a1, a2, one can discover that the focusing performance is more evident for the RPCAiGXBs. More concretely, the maximum intensity at the focused position for the RPCAiGXBs is even greater than the initial value as we can see from the triangle line in Fig. 5a1. To conclude, by controlling $\chi _0$, we are able to modulate the propagating trajectory, the velocity of the main lobes, the focused performance and the intensity of the RPCAiGBs.

Fig. 6

Side-view evolution of the RPCAiGXBs and the RPCAiGYBs through uniaxial crystals orthogonal to the optical axis in z–x plane (the first row) and z–y plane (the second row) and the velocities of the RPCAiGXBs (c1–c2) and the RPCAiGYBs (c3) in the x and y directions with varying $\beta$ when $\chi _0=0.1$ and $n_\mathrm{e}=1.5n_\mathrm{o}$

Here, we center around the impacts of the first-order chirp parameter $\beta$ depicted in Fig. 6 and we consider $\chi _0=0.1$ and $n_\mathrm{e}=1.5n_\mathrm{o}$ in this situation. Figure 6a1, a2, b1, b2 are the side-view intensity distribution of the RPCAiGXBs while Fig. 6a3, a4, b3, b4 are those of the RPCAiGYBs. The graphs mentioned above evidently demonstrate that $\beta$ plays a crucial rule in the trajectories of the RPCAiGXBs and the RPCAiGYBs. We are easily able to conclude that as the first-order chirp parameter increases, the propagation trajectories of the RPCAiGXBs and the RPCAiGYBs both move downwards in the x and y directions. So, we can deduce that the propagation trajectory of the RPCAiGBs also moves downwards in the x and y directions as $\beta$ getting larger. Furthermore, we plot the velocities of the main lobes of the RPCAiGXBs and the RPCAiGYBs along the x and y directions in Fig. 6c1–c3. One can see that generally, the magnitude of the velocity decreases at first and then rises in the opposite direction. Besides, the acceleration of the beams is the same when $\beta$ is different but the magnitude of the initial velocity is higher when $\beta$ is larger. In the end, we conclude that one can modulate the propagation trajectory and the velocity of the RPCAiGBs by controlling $\beta$.

Fig. 7

The maximum intensity distribution of the RPCAiGXBs (a1) through uniaxial crystals orthogonal to the optical axis as a function of z in the circumstance of varying $n_\mathrm{e}/n_\mathrm{o}$ and intensity distribution on z–x plane (b1, b2) and z–y plane (b3)–(b4) when $n_\mathrm{e}/n_\mathrm{o}$ is taken to be 1.2 and 1.8. The parameters are chosen as $\chi _0=0.1$ and $\beta =0.5$

Finally, we concentrate on the influences caused by $n_\mathrm{e}/n_\mathrm{o}$. Referring to Eqs. (6–7) and (11–18), we find that the RPCAiGXBs are affected by $n_\mathrm{e}$ and $n_\mathrm{o}$ while the RPCAiGYBs are only influenced by $n_\mathrm{o}$. So, we only discuss the effects of $n_\mathrm{e}/n_\mathrm{o}$ on the RPCAiGXBs which are also identical to those of the RPCAiGBs. Above all, we first consider the situation when $n_\mathrm{e}/n_\mathrm{o}\ne 1$ (in anisotropic circumstance). As we can tell from Fig. 7a1, the focusing position will be closer to the initial plane and focused performance will be more evident as the ratio of $n_\mathrm{e}$ to $n_\mathrm{o}$ gets larger. After propagating a certain distance, the maximum intensity increases slightly owing to the fact that focusing is stronger than diffraction but later the influence of diffraction is stronger so it declines afterwards. Then, we take $n_\mathrm{e}/n_\mathrm{o}=1.2$ and $n_\mathrm{e}/n_\mathrm{o}=1.8$ as examples to discuss as displayed in Fig. 7b1–b4. One can see that the focusing performance is more compelling when $n_\mathrm{e}/n_\mathrm{o}=1.8$ [see Fig. 7b1–b2] and the acceleration is different in the x and y directions when changing $n_\mathrm{e}/n_\mathrm{o}$. More specifically, as the ratio of $n_\mathrm{e}/n_\mathrm{o}$ increases, the acceleration in the x direction is stronger while that in the y direction is weaker. When it comes to $n_\mathrm{e}/n_\mathrm{o}=1$ (in isotropic circumstance), the maximum intensity reduces monotonously and there is not a peak value, which means that the focusing performance does not exist in this situation. Nonetheless, we can still find some similarities while $n_\mathrm{e}/n_\mathrm{o}$ is different. For example, the initial maximum intensity of the RPCAiGXBs is the same even though the values of $n_\mathrm{e}/n_\mathrm{o}$ are diverse.

Fig. 8

The maximum intensity distribution of the RPCAiGBs through uniaxial crystals orthogonal to the optical axis as a function of the x direction (the first row) and the y direction (the second row) when $n_\mathrm{e}/n_\mathrm{o}$ is taken to be 1.2 and 1.8. The parameters are chosen as $\beta =0.5$ and $\chi _0=0.1$

Fig. 9

The intensity distribution of the RPCAiGBs through uniaxial crystals orthogonal to the optical axis in z–x plane (a1–a2), z–y plane (a3–a4) and x–y plane (b1–b4) when $n_\mathrm{e}/n_\mathrm{o}$ is equal to 1.2 and 1.8. The parameters are chosen as $\beta =0.5$ and $\chi _0=0.1$

To further reveal the acceleration and intensity focusing properties of the RPCAiGBs under the impacts of $n_\mathrm{e}/n_\mathrm{o}$ through uniaxial crystals orthogonal to the optical axis, the maximum intensity distribution of the RPCAiGBs as a function of the x and y directions and intensity distribution in various view planes when $\beta =0.5$ and $\chi _0=0.1$ are shown in Figs. 8 and 9. Originally, the intensity distribution of the RPCAiGBs along the x and y directions is similar when $n_\mathrm{e}/n_\mathrm{o}$ is different. When Z = 10Z_r, if $n_\mathrm{e}/n_\mathrm{o}$ gets larger, the acceleration in the x direction is faster while the one in the y direction is slower. Apart from that, when $n_\mathrm{e}/n_\mathrm{o}=1.8$, the maximum intensity of the RPCAiGBs is smaller at Z = 1Z_r, whereas it becomes greater at Z = 10Z_r. Figure 9a1–a4 depict the side-view propagation of the beams. One can see that when $n_\mathrm{e}/n_\mathrm{o}=1.8$, the deflection in the x direction is stronger while the one in the y direction is weaker. What is more, it is revealed in Fig. 9b1–b4 that $n_\mathrm{e}/n_\mathrm{o}$ has an impact on the focused position. More concretely, if $n_\mathrm{e}/n_\mathrm{o}=1.2$, a smaller value, the focused point is Z = 17Z_r while if $n_\mathrm{e}/n_\mathrm{o}=1.8$, a larger value, the focused point is Z = 12Z_r. These also coincide with the conclusions we get from Fig. 8. In summary, one can control the focused performance and the deflection degree by setting appropriate $n_\mathrm{e}/n_\mathrm{o}$.

4 Conclusion

Analytical propagation expressions of the x and y components of the RPCAiGBs in uniaxial crystals orthogonal to the optical axis have been derived. Our results show that at first, the intensity of the RPCAiGXBs and RPCAiGYBs flows along the x and y directions individually and, finally, the intensity of these two components both propagates along the x direction to the side lobes. In addition, the bending degree of the RPCAiGXBs in the x direction is clearer than that in the y direction, while the bending degree of the RPCAiGYBs in the x and y directions is the same. Then, we investigate the impacts of $\chi _0$ which enhance the propagation deviation with a smaller value. Also, the RPCAiGBs propagate like the RPCAiBs when $\chi _0$ is set as a small value while the beams act like the RPCGBs with a large one. By controlling the $\chi _0$, one can modulate the focusing performance of the PRCAiGXBs and the RPCAiGYBs. More precisely, when $\chi _0$ is small, there is a focusing performance at a certain propagation distance and the peak value of the maximum intensity is higher while it acts oppositely when $\chi _0$ is large. With respect to the influence of $\beta$, the trajectories descend in the x and y directions for both the RPCAiGXBs and the RPCAiGYBs with a larger value. Equations (11–18) indicate that $n_\mathrm{e}/n_\mathrm{o}$ only affects the RPCAiGXBs but has no influence on the RPCAiGYBs if $n_\mathrm{o}$ is fixed. In anisotropic circumstance, the focusing performance appears and the maximum intensity of the focused point is bigger when $n_\mathrm{e}/n_\mathrm{o}$ is larger. Additionally, the acceleration of the x and y components in the x direction is larger, while that in the y direction is slower with larger $n_\mathrm{e}/n_\mathrm{o}$ which means that with an increase of $n_\mathrm{e}/n_\mathrm{o}$, the bending degree of the RPCAiGBs is stronger in the x direction but weaker in the y direction.