Atom localization in five-level atomic system driven by an additional incoherent pump

Abstract

We propose a new scheme for two-dimensional (2D) and three-dimensional (3D) atom localization via spatial quantum interference in a five-level atomic system driven by an additional incoherent pump. Because of the position-dependent atom–field interaction, the position information of the atom can be obtained by the measurement of the probe absorption. We find that the 3D atom localization is obtained with high precision by adjusting the incoherent pump. In particular, we show that adjusting the incoherent pump can lead to a redistribution of the atoms and a significant change in the visibility of the interference pattern. As a result, the atom can be localized in volumes that are substantially smaller than a cubic optical wavelength.

1 Introduction

Atom localization, one of the most intriguing effects in quantum optics, has became an active research topic because of its potential applications in atom nanolithography [1] and the measurement of center-of-mass wave function of moving atoms [2]. Based on atomic coherence, many schemes were proposed for control of atom localization in one and two dimensions [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Recently, by interacting with three orthogonal standing-wave fields, some schemes have also been used to achieve three-dimensional (3D) atom localization. For instance, a scheme for 3D atom localization was proposed by Ivanov et al. using the measurement of the atomic-level population in a four-level tripod-type atomic system [21]. Hamedi and Juzeliunas [22] have been put forward for 3D atom localization scheme in a five-level atom-light coupling configuration, in which the effect of the relative phase of the applied fields was considered. Quite recently, Zhu et al. [23] proposed an efficient scheme for high-precision 3D atom localization via spatial interference in a generic double two-level atomic system driven by a weak probe field and three mutually perpendicular standing-wave fields.

In this work, we investigate the 2D and 3D localization behaviors in a five-level atomic system in which an incoherent pump is applied. Our work is related to references [21,22,23,24], but our scheme displays certain differences. First, we have discussed the influence of the incoherent pump on 2D and 3D localization behaviors, which may offer a great possibility to localize the atom at a given position with high localization precision and spatial resolution under appropriate conditions. Second, by properly modulating the incoherent pump, we can localize the atom at a particular position in three dimensions, and the conditional probability and precision can be improved greatly compared to the schemes discussed in [21,22,23,24]. Furthermore, our scheme is based on the probe-absorption measurement, which is much easier to carry out in the practical experiment compared with the spontaneous-emission measurement scheme [24].

2 The model and dynamic equation

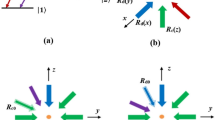
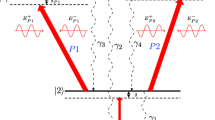
We consider a five-level atomic system shown in Fig. 1. This model has been proposed previously in a different context for high refractive index contrast with low absorption [25]. The transitions $\left| 2 \right\rangle \leftrightarrow \left| 4 \right\rangle$ and $\left| 3 \right\rangle \leftrightarrow \left| 5 \right\rangle$ are driven by two coherent laser fields with Rabi frequencies $\varOmega_{1}$ and $\varOmega_{2}$, respectively, and a weak probe is coupled to both transitions $\left| 1 \right\rangle \leftrightarrow \left| 4 \right\rangle$ and $\left| 4 \right\rangle \leftrightarrow \left| 5 \right\rangle$ with Rabi frequencies $\varOmega_{p1}$ and $\varOmega_{p2}$, respectively. An incoherent pump field with a rate $\varLambda$ is applied to transition $\left| 1 \right\rangle \leftrightarrow \left| 4 \right\rangle$. In the following discussion, we consider 2D and 3D atom localization behaviors that the atom interacts with the standing-wave fields. In the 2D atom localization, we take $\varOmega_{1}$ and $\varOmega_{2}$ as two orthogonal standing-wave laser fields that couple two different atomic transitions, respectively, i.e. $\varOmega_{1} = \varOmega_{m} \sin (kx) + \varOmega_{a}$ and $\varOmega_{2} = \varOmega_{n} \sin (ky) + \varOmega {}_{b}$. In the 3D atom localization, we take $\varOmega_{2}$ as the composition of two orthogonal standing waves with the same frequency that drives the transition $\left| 3 \right\rangle \leftrightarrow \left| 5 \right\rangle$, while $\varOmega_{1}$ corresponds to a standing-wave field, i.e. $\varOmega_{2} = \varOmega_{yz} [\sin (ky) + \sin (kz)]$ and $\varOmega_{1} = \varOmega_{x} \sin (kx) + \varOmega_{c}$.

Fig. 1

a Schematic diagram of a closed Λ-type three-level atomic system, b an atom moves along the z axis, interacting with two orthogonal standing-wave fields in the x–y plane, and c $\varOmega_{2} (y)$ and $\varOmega_{2} (z)$ are the combinations of two orthogonal standing-wave fields aligning along the corresponding y and z directions, respectively, $\varOmega_{1} (x)$ is the standing-wave field aligning along the x direction, and the probe field and incoherent pump field propagate along the z direction

In dipole and rotating-wave approximation, the Hamiltonian of the system in the interaction picture can be written as [26,27,28]

$$ \begin{aligned} H_{I} /\hbar & = - (\Delta_{p1} - \Delta_{1} )\left| 2 \right\rangle \left\langle 2 \right| - (\Delta_{p1} + \Delta_{p2} - \Delta_{2} )\left| 3 \right\rangle \left\langle 3 \right| - \Delta_{p1} \left| 4 \right\rangle \left\langle 4 \right| \\ & \quad {\kern 1pt} - (\Delta_{p1} + \Delta_{p2} )\left| 5 \right\rangle \left\langle 5 \right| - (\varOmega_{p1} \left| 4 \right\rangle \left\langle 1 \right| + \varOmega_{p2} \left| 5 \right\rangle \left\langle 4 \right| + \varOmega_{1} \left| 4 \right\rangle \left\langle 2 \right| + \varOmega_{2} \left| 5 \right\rangle \left\langle 3 \right| + H.c.), \\ \end{aligned} $$

(1)

here $\Delta_{p1} = \omega_{p} - \omega_{41}$, $\Delta_{p2} = \omega_{p} - \omega_{54}$, $\Delta_{1} = \omega_{1} - \omega_{42}$, and $\Delta_{2} = \omega_{2} - \omega_{53}$ are the detunings of the laser fields. The five states $\left| 1 \right\rangle$, $\left| 2 \right\rangle$, $\left| 3 \right\rangle$, $\left| 4 \right\rangle$ and $\left| 5 \right\rangle$ correspond to ${}^{ 8 5}{\text{Rb}}$ atomic levels $5{\text{S}}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} (F = 2)$, $5{\text{S}}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} (F = 2)$, $5{\text{S}}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} (F = 3)$, $5{\text{P}}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} (F = 3)$ and $4{\text{D}}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} (F = 3)$, respectively.

The master equation of motion is as follows:

$$ \dot{\rho } = - \frac{i}{\hbar }[H_{I} ,\rho ] - L\rho , $$

(2)

and $L\rho$ represents the incoherent contributions given by

$$ L\rho = L_{41}^{\gamma } \rho + L_{42}^{\gamma } \rho + L_{53}^{\gamma } \rho + L_{54}^{\gamma } \rho + L^{d} \rho + L^{\varLambda } \rho , $$

(3a)

$$ L_{jk}^{\gamma } \rho = \frac{{\varGamma_{jk} }}{2}\left( {\left| j \right\rangle \left\langle j \right|\rho + \rho \left| j \right\rangle \left\langle j \right| - 2\left| k \right\rangle \left\langle j \right|\rho \left| j \right\rangle \left\langle k \right|} \right), $$

(3b)

$$ L^{d} \rho = \sum\limits_{j \ne k} {\gamma_{jk}^{d} \left| j \right\rangle \left\langle k \right|} , $$

(3c)

$$ L^{\varLambda } \rho = \frac{\varLambda }{2}\left( {\left| 1 \right\rangle \left\langle 1 \right|\rho + \rho \left| 1 \right\rangle \left\langle 1 \right| - 2\left| 4 \right\rangle \left\langle 1 \right|\rho \left| 1 \right\rangle \left\langle 4 \right|} \right), $$

(3d)

where $L_{jk}^{\gamma } \rho$ describes spontaneous emission from $\left| j \right\rangle$ to $\left| k \right\rangle$ with rate $\varGamma_{jk}$. The second term, $L^{d} \rho$, models additional pure dephasing for $\rho_{jk}$ with rate $\gamma_{jk}^{d}$, such that the total damping rate of this coherence is $\gamma_{jk} = \gamma_{jk}^{d} + (\varGamma_{j} + \varGamma_{k} )/2$, with $\varGamma_{j} = \sum_{k} \varGamma_{jk}$ being the total decay rate out of state $\left| j \right\rangle$. The third contribution $L^{\varLambda } \rho$ describes the incoherent pumping from $\left| 1 \right\rangle$ to $\left| 4 \right\rangle$ with rate $\varLambda$.

We assume the probe field to be weak enough to be treated as a perturbation to the system in linear order. The related zeroth-order [superscript (0)] and first-order [superscript (1)] contributions for $\rho_{ij}$ are obtained [29] as

$$ \rho_{11}^{(0)} = \frac{{2\gamma_{42} \varGamma_{41} \varOmega_{1}^{2} }}{{\varLambda \gamma_{42}^{2} \varGamma_{42} + \varLambda \varGamma_{42} \Delta_{1}^{2} + 2\gamma_{42} (2\varLambda + \varGamma_{41} )\varOmega_{1}^{2} }}, $$

(4a)

$$ \rho_{22}^{(0)} = \frac{{\varLambda \left( {\gamma_{42}^{2} \varGamma_{42} + \varGamma_{42} \Delta_{1}^{2} + 2\gamma_{42} \varOmega_{1}^{2} } \right)}}{{\varLambda \gamma_{42}^{2} \varGamma_{42} + \varLambda \varGamma_{42} \Delta_{1}^{2} + 2\gamma_{42} \left( {2\varLambda + \varGamma_{41} } \right)\varOmega_{1}^{2} }}, $$

(4b)

$$ \rho_{44}^{(0)} = \frac{{2\varLambda \gamma_{42} \varOmega_{1}^{2} }}{{\varLambda \gamma_{42}^{2} \varGamma_{42} + \varLambda \varGamma_{42} \Delta_{1}^{2} + 2\gamma_{42} \left( {2\varLambda + \varGamma_{41} } \right)\varOmega_{1}^{2} }}, $$

(4c)

$$ \rho_{55}^{(0)} = 0 $$

(4d)

$$ \rho_{41}^{(1)} = \frac{{\left( {\rho_{44}^{(0)} - \rho_{11}^{(0)} } \right)\varOmega_{p1} }}{{\Delta_{p1} + i\left( {\gamma_{41} + \frac{\varLambda }{2}} \right) + \frac{{\varOmega_{1}^{2} }}{{\Delta_{1} - \Delta_{p1} - i(\gamma_{21} + \varLambda /2)}}}}, $$

(4e)

$$ \rho_{54}^{(1)} = \frac{{f_{1} \left( {\rho_{44}^{(0)} - \rho_{55}^{(0)} } \right)\varOmega_{p2} }}{{f_{2} }}, $$

(4f)

here the coefficients are given by

$$ \begin{aligned} f_{1} & = - i[ - \gamma_{32} - i(\Delta_{2} - \Delta_{p2} - \Delta_{1} )][( - i\gamma_{32} + \Delta_{2} - \Delta_{p2} - \Delta_{1} )(i\gamma_{52} + \Delta_{p2} + \Delta_{1} ) \\ & \quad + \varOmega_{2}^{2} - \varOmega_{1}^{2} ]\left\{ {\gamma_{43} + i(\Delta_{2} - \Delta_{p2} ) + \frac{{\varOmega_{1}^{2} }}{{\gamma_{32} + i(\Delta_{2} - \Delta_{p2} - \Delta_{1} )}} + } \right. \\ & \quad {\kern 1pt} {\kern 1pt} \left. {\frac{{\varOmega_{1}^{2} [(i\gamma_{43} - \Delta_{2} + \Delta_{p2} )( - i\gamma_{32} + \Delta_{2} - \Delta_{p2} - \Delta_{1} ) - \varOmega_{2}^{2} + \varOmega_{1}^{2} }}{{[\gamma_{32} + i(\Delta_{2} - \Delta_{p2} - \Delta_{1} )][( - i\gamma_{32} + \Delta_{2} - \Delta_{p2} - \Delta_{1} )(i\gamma_{52} + \Delta_{p2} + \Delta_{1} ) + \varOmega_{2}^{2} - \varOmega_{1}^{2} ]}}} \right\}, \\ \end{aligned} $$

$$ \begin{aligned} f_{2} & = \left[ {\gamma_{32} + \gamma {}_{54} + i(\Delta_{2} - 2\Delta_{p2} - \Delta_{1} )} \right]\varOmega_{1}^{2} \left[ {(i\gamma_{43} - \Delta_{2} + \Delta_{p2} )( - i\gamma_{32} + \Delta_{2} - \Delta_{p2} - \Delta_{1} ) - \varOmega_{2}^{2} + \varOmega_{1}^{2} } \right]{\kern 1pt} \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left[ {( - i\gamma_{32} + \Delta_{2} - \Delta_{p2} - \Delta_{1} )(i\gamma_{52} + \Delta_{p2} + \Delta_{1} ) + \varOmega_{2}^{2} - \varOmega_{1}^{2} } \right]\left\{ {\left[ {\gamma_{32} + i(\Delta_{2} - \Delta_{p2} - \Delta_{1} )} \right]} \right. \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \times \left. {\left[ {( - i\gamma_{43} + \Delta_{2} - \Delta_{p2} )(i\gamma_{54} + \Delta_{p2} ) + \varOmega_{2}^{2} } \right] + (\gamma_{54} - i\Delta_{p2} )\varOmega_{1}^{2} } \right\}, \\ \end{aligned} $$

Then, the linear susceptibility of the probe field can be written as

$$ \chi = \frac{{3N\lambda_{p}^{3} }}{{8\pi^{2} }}\left( {\frac{{\varGamma_{41} \rho_{41}^{(1)} }}{{\varOmega_{p1} }} + \frac{{\varGamma_{54} \rho_{54}^{(1)} }}{{\varOmega_{p2} }}} \right), $$

(5)

here $N$ is the atomic density and $\lambda_{p}$ is the wave length of the probe field. It is well known that the imaginary part of the susceptibility $\text{Im} (\chi )$ accounts for absorption of the probe field, which depends on the position of the atom moving in the three orthogonal standing waves, i.e., the probe absorption can provide the position information of the atom.

3 Results and discussion

In this section, we analyze the conditional position probability distribution of the atom via a few numerical calculations based on the probe absorption $\text{Im} (\chi )$, and demonstrate 2D and 3D atom localization behaviors by measuring probe absorption. Here, a realistic candidate for the proposed atomic system can be found in [25, 29]. For such a case, parameters are chosen as $\varGamma_{41} = \varGamma_{42} = 6{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varGamma_{54} = 1.5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{MHz}}$, $N = 2.1 \times 10^{14} {\kern 1pt} {\kern 1pt} {\text{cm}}^{ - 3}$, $\gamma_{54} = 2 1 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and $\gamma_{41} = \gamma_{42} = \gamma_{43} = 1 0 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$.

3.1 2D localization

First of all, we consider the 2D atom localization where a standing-wave field $\varOmega_{1} = \varOmega_{m} \sin (kx) + \varOmega_{a}$ drives atomic transition $\left| 2 \right\rangle \leftrightarrow \left| 4 \right\rangle$, while the atomic transition $\left| 3 \right\rangle \leftrightarrow \left| 5 \right\rangle$ is driven by another standing-wave field $\varOmega_{2} = \varOmega_{n} \sin (ky) + \varOmega_{b}$.

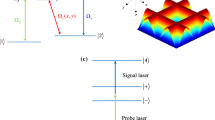
The probe absorption $\text{Im} (\chi )$ versus the positions ($kx,ky$) for different probe detuning $\Delta_{p2}$ is plotted in Fig. 2. As can be seen, the probe absorption $\text{Im} (\chi )$ depend strongly on the detuning $\Delta_{p2}$. On the condition of $\Delta_{p2} = 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the probe absorption are distributed in four different quadrants (Fig. 2a). When the detuning is tuned to $\Delta_{p2} = 8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{MHz}}$, the peak maxima of probe absorption are mainly localized in x–y plane with four crater-like patterns (Fig. 2b). When the detuning is increased to $\Delta_{p2} = 1 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, we obtain four narrow localization peaks. The resulting absorption exhibits four spike-like patterns (Fig. 2c). However, in the case of $\Delta_{p2} = 1 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 2d), the probe absorption is distributed in four different quadrants with low value, which implies that too large probe detuning will bring a destructive effect to the precision of 2D atom localization.

Fig. 2

The probe absorption $\text{Im} (\chi )$ versus positions ($kx/\pi$,$ky/\pi$) for a $\Delta_{p2} = 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$; b $\Delta_{p2} = 8{\kern 1pt} {\kern 1pt} {\text{MHz}}$; c $\Delta_{p2} = 10{\kern 1pt} {\kern 1pt} {\text{MHz}}$; and d $\Delta_{p2} = 10.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are $\Delta_{p1} = 0.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\Delta_{1} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\Delta_{2} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varLambda = 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{m} = 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{n} = 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{a} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, and $\varOmega_{b} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$

In Fig. 3, we investigate how the probe absorption depends on the intensities of the coherent coupling fields $\varOmega_{i} (i = a,b)$. For $\varOmega_{a} = 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and $\varOmega_{\text{b}} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the peak maxima are situated in the first and second quadrants with two spike-like patterns (Fig. 3a). In the case of $\varOmega_{a} = 1.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and $\varOmega_{b} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, one can find that there are two crater-like patterns in the first and second quadrants (Fig. 3b). Interestingly, when the coherent coupling fields are $\varOmega_{a} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and $\varOmega_{b} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 3c), the localization peak in the second quadrant is completely disappeared. For the case that $\varOmega_{a} = 0. 6{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and $\varOmega_{b} = 0. 6{\kern 1pt} {\kern 1pt} {\text{MHz}}$, it can be seen that there is only a crater-like pattern in the first quadrant (Fig. 3d). These results allow us to say that, via adjusting the two coherent coupling fields, high-precision and high-efficiency 2D atom localization is obtained.

Fig. 3

The probe absorption $\text{Im} (\chi )$ versus positions ($kx/\pi$, $ky/\pi$) for a $\varOmega_{a} = 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{b} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$; b $\varOmega_{a} = 1.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{b} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$; c $\varOmega_{a} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{b} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$; and d $\varOmega_{a} = 0. 6{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{b} = 0. 6{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are the same as Fig. 2c

To show the dependence of the 2D atom localization on the rate of the incoherent pump field, we show the effects of the rate $\varLambda$ on the probe absorption in Fig. 4. When the rate of the incoherent pump field is adjusted to $\varLambda = 0.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the probe absorption $\text{Im} (\chi )$ shows two wave-like patterns and a spike-like pattern in first quadrant (Fig. 4a). However, on the condition of $\varLambda = 1.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 4b), the probe absorption displays two inverted wave-like patterns and a spike-like pattern located at the positions $(kx/\pi ,ky/\pi ) = (0.5,0.5)$. In this case, two inverted wave-like packets indicate $\text{Im} (\chi ) < 0$, which corresponds to the probe field is amplified. In other words, by appropriately adjusting the rate of the incoherent pump field, the 2D atom localization observed here occurs via measuring both the probe absorption and gain. In addition, the position-dependent patterns are novel, which are quite different from the earlier proposals [11,12,13,14, 16, 18, 20].

Fig. 4

The probe absorption $\text{Im} (\chi )$ versus positions ($kx/\pi$, $ky/\pi$) for a $\varLambda = 0.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$; b $\varLambda = 1.5{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are the same as Fig. 3c

3.2 3D localization

In this section, we take $\varOmega_{2}$ as the composition of two orthogonal standing waves with the same frequency that drives the transition $\left| 3 \right\rangle \leftrightarrow \left| 5 \right\rangle$, while $\varOmega_{1}$ corresponds to a standing-wave field, i.e. $\varOmega_{2} = \varOmega_{yz} [\sin (ky) + \sin (kz)]$ and $\varOmega_{1} = \varOmega_{x} \sin (kx) + \varOmega_{c}$, and then address how the system parameters can be used to achieve 3D atom localization.

The probe absorption $\text{Im} (\chi )$ versus the positions ($kx,ky,kz$) for different probe detuning $\Delta_{p2}$ is plotted in Fig. 5. When $\Delta_{p2} = 1 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, it can be seen that the probe absorption is distributed in different subspaces of the 3D space (Fig. 5a). When the probe detuning is tuned to $\Delta_{p2} = 1 3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{MHz}}$, the probe absorption is located in four subspaces with four spheres (Fig. 5b). For the case $\Delta_{p2} = 1 4. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the probe absorption is also situated in four subspaces of the 3D space (Fig. 5c), but the volume of the sphere in each subspace becomes small. Furthermore, when the probe detuning is detected at an appropriate value (i.e. $\Delta_{p2} = 1 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$ Fig. 5d), the probe absorption exhibits four much smaller spheres in the four different subspaces. In such a case, we can achieve much better spatial resolution in the condition position probability distribution of the atom. The reasons for the above results can be qualitatively explained as follows. From Eq. (5), it is straight forward to show that there is a strong correlation between the probe detuning $\Delta_{p2}$ and the probe absorption; the varying probe detuning will alter the absorption of the atom medium, and then influences the spatial distribution of the probe absorption. Consequently, we can observe different localization structures in Fig. 5.

Fig. 5

Isosurfaces for the probe absorption $\text{Im} (\chi ) = 0.01$ versus positions ($- 1 \le kx/\pi \le 1$, $- 1 \le ky/\pi \le 1$, $- 1 \le kz/\pi \le 1$) for different values of $\Delta_{p2}$. a $\Delta_{p2} = 1 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$; b $\Delta_{p2} = 13{\kern 1pt} {\kern 1pt} {\text{MHz}}$; c $\Delta_{p2} = 1 4. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$; and d $\Delta_{p2} = 15{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are $\Delta_{p1} = 1 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\Delta_{1} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\Delta_{2} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varLambda { = }1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{p1} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{p2} = 0. 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{c} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{x} = 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$, $\varOmega_{yz} = 5{\kern 1pt} {\kern 1pt} {\text{MHz}}$

In Fig. 6, we study the effect of the coupling field $\varOmega_{c}$ on the 3D atom localization. In the case of $\varOmega_{c} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the maxima of the probe absorption are distributed in four subspaces (Fig. 6a). But under the condition of $\varOmega_{c} = 0.1{\kern 1pt} {\kern 1pt} {\text{MHz}}$, the probe absorption are distributed in four subspaces with different localization precision, in which the probe absorption in the subspaces ($- x$, $- y$, $- z$) and ($- x$, $y$, $z$) displays two small-diameter spheres with high precision and the probe absorption in the subspaces ($x$, $- y$, $- z$) and ($x$,$y$,$z$) exhibits two large-diameter spheres with low precision, which leads to the localization of the atom at these spheres (Fig. 6b). When the probe detuning is tuned to $\varOmega_{c} = 0.2{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 6c), it is easy to see that the two spheres in the subspaces ($- x$, $- y$, $- z$) and ($- x$, $y$, $z$) becomes smaller while the two spheres in the subspaces ($x$, $- y$, $- z$) and ($x$, $y$, $z$) becomes bigger. Most interestingly, as we further increase the coupling field $\varOmega_{c}$ to $0. 3{\kern 1pt} {\kern 1pt} {\text{MHz}}$, two spheres in the subspaces ($- x$, $- y$, $- z$) and ($- x$, $y$, $z$) are completely disappeared and the maxima of the probe absorption situated in two spheres as shown in Fig. 6d. In such a condition, the probability of finding the atom in 3D space is increased to 1/2, which is a significant advantage of our proposed scheme.

Fig. 6

Isosurfaces for the probe absorption $\text{Im} (\chi ) = 0.01$ versus positions ($- 1 \le kx/\pi \le 1$, $- 1 \le ky/\pi \le 1$, $- 1 \le kz/\pi \le 1$) for different values of $\varOmega_{c}$. a $\varOmega_{c} = 0{\kern 1pt} {\kern 1pt} {\text{MHz}}$; b $\varOmega_{c} = 0. 1{\kern 1pt} {\kern 1pt} {\text{MHz}}$; c $\varOmega_{c} = 0. 2{\kern 1pt} {\kern 1pt} {\text{MHz}}$; and d $\varOmega_{c} = 0. 3{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are the same as Fig. 5d

In Fig. 7, we show the probe absorption versus the positions ($kx,ky,kz$) for four different rates of the incoherent pump $\varLambda$, it is easy to see that the probe absorption in the case of $\varLambda { = 1}{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 7a) is distributed in two subspaces ($x$, $- y$, $- z$) and ($x$, $y$,$z$). As we increase $\varLambda$ from $1$ to $2{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 7b), two small spheres in the subspaces ($- x$, $- y$, $- z$) and ($- x$, $y$, $z$) appear. As we further increase $\varLambda$ to $3{\kern 1pt} {\kern 1pt} {\text{MHz}}$ and then to $4{\kern 1pt} {\kern 1pt} {\text{MHz}}$ (Fig. 7c, d), the volume of the spheres in the subspaces ($- x$,$- y$, $- z$) and ($- x$, $y$,$z$) becomes more and more larger. This suggests, by increasing the rate $\varLambda$, that the localization precision is reduced and the probability of finding the atom in 3D space is increased to 1/4. Based on the above analysis, it is straightforward to show that high-precision 3D atom localization is obtained only when $\varLambda$ reaches a proper value.

Fig. 7

Isosurfaces for the probe absorption $\text{Im} (\chi ) = 0.01$ versus positions ($- 1 \le kx/\pi \le 1$, $- 1 \le ky/\pi \le 1$, $- 1 \le kz/\pi \le 1$) for different values of $\varLambda$. a $\varLambda { = 1}{\kern 1pt} \;{\text{MHz}}$; b $\varLambda { = 2}{\kern 1pt} {\kern 1pt} {\text{MHz}}$; c $\varLambda { = 3}{\kern 1pt} {\kern 1pt} {\text{MHz}}$; and d $\varLambda { = 4}{\kern 1pt} {\kern 1pt} {\text{MHz}}$. The other parameters are the same as Fig. 5d

4 Conclusions

In conclusion, we have proposed a scheme for 2D and 3D atom localization behaviors in a five-level atomic system in which an incoherent pump is applied. Due to the position-dependent atom–field interaction, the position information of the atom in the standing-wave fields can be obtained by the probe absorption. More importantly, the precision and spatial resolution of 2D and 3D atom localization behaviors are improved via an incoherent pump, which is a significant advantage that previous schemes [11,12,13,14,15,16,17,18,19,20,21,22,23,24] do not have. As a result, our scheme may be helpful in optical imaging [30], laser cooling or atom nano-lithography via atom localization.

Finally, it is pointed out that we do not consider the effect of atomic motion and hence, there is no the Doppler-free broadening effect in our treatment. Consequently, the results here are suitable only for the cold atoms.