1 Introduction

The process of sequential casting [1] of steel is the most diffused industrial approach for the production of different grades of steel, i.e. materials characterized by a different elemental composition of the alloy. The possibility of locating precisely the transition zone between two consecutive grades is of great interest for the steel industry, since the material in the transition layer cannot be re-cast and must be disposed as a waste. An accurate determination of the length of the transition zone would minimize the amount of material to be discarded and, thus, would have an important economic and environmental advantage with respect to the current approach, which purposely overestimates the length of the transition zone, for safety reasons.

A joint European effort, funded in the framework of the CE research fund for coal and steel (RFCS), has been developed in last years with the purpose of accurately modelling the sequential cast process and determining experimentally, using the laser-induced breakdown spectroscopy (LIBS) technology [2], the variation of the steel composition during the process of sequential casting.

The results of this project, named LACOMORE (laser-based continuous monitoring and resolution of steel grades in sequence casting machines) have evidenced that the mixing of the steel grades during the process is not homogeneous, and this may affect the spatial homogeneity of the final product. Therefore, it became evident the need for developing theoretical models of the sequential casting process that should take into account the effect of imperfect mixing of the material in the tundish, during the casting process [3,4,5].

Several models have been proposed, in recent years, of the continuous casting process [6,7,8,9]. Most of them, however, implies a deep knowledge of the geometry of the system, and are difficult to implement in the steel factory everyday use. More recently, Mier Vasallo et al. [10] proposed a simple mathematical model, capable of predicting reliably the change in elemental concentration in the transition between two different steel grades.

In this paper, we present the extension of this model, which implies a perfect and instantaneous mixing of the different steel grades, to take into account that the mixing process in the tundish occurs on a time scale not negligible with respect to the typical duration of the transition between two sequential grades. We will then compare the prediction of this improved method with the results of the LIBS analysis of the steel composition in the transition zone.

2 The process of sequential casting

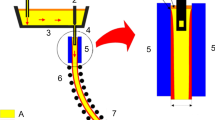
The process of sequence casting of steel occurs in a reservoir, called tundish, which can be filled up to a volume Vmax. In this process, the composition of the material is varied continuously by adding the material corresponding to the new steel grade to the remains of the material of the previous one, which at time t = 0 occupy a volume V0 of the tundish. The new material is introduced in the tundish at time t = 0 at a rate A(t) (m3/min), while the tundish is emptied through one or more strands at a constant rate B (m3/min). The sequential casting process is sketched in Fig. 1.

Fig. 1
figure 1

Schematic representation of the sequential casting process. For simplicity, a single-output strand is considered

Full size image

3 Current modelling of the sequential casting process

A precise description of the sequential casting process would imply the use of complex hydrodynamic equations, which should take into account the exact geometry of the tundish and the output strand(s) (see, for example, Ref. [11]). However, a simple one-dimensional model of the transition between different steel grades in a sequential casting machine has been developed and patented by one of the authors (DMV) [10]. According to this model, the transition of the concentration of a given element during the process of changing of the steel grade is represented by two coupled first-grade differential equations. To ease the comprehension, a list of the symbol used (with the corresponding units) is reported in Table 1.

Table 1 Nomenclature
Full size table

Assuming at time t = 0 a volume in the tundish equal to V0 of the first grade of steel, with a concentration C1 of a given element, we can express the variation of the steel volume in the tundish with time as:

$$V\left( {t\; + \;\Delta t} \right)\; = \;V\left( t \right)\; + \;A(t)\Delta t - B\Delta t,$$
(1)

where A(t) represents the input flux of the material with a concentration C2 of the same element (second grade steel) and B is the output flux (for the sake of simplicity, a single-output strand is assumed). The model is easily generalized to take into account the presence of an arbitrary number n of output strands.

Since the maximum volume of the tundish cannot be exceeded, we can assume a variable input flux:

$$A\left( t \right)\; = \;K \left( {V_{ \hbox{max} } \; - \;V(t)} \right)\; + \;B,$$

which corresponds to the following V(t) dependence:

$$V\left( t \right)\; = \; \left( {V_{ \hbox{max} } - V_{0} } \right)\left( {1 - e^{{ - \frac{t}{{\tau_{0} }}}} } \right)\; + \;V_{0} ,$$
(2)

where K = 1/τ0 represents the rate at which the tundish is filled.

Alternatively, we can assume a constant input flux rate A(t) > n B until V(t) = Vmax, while after that time the input flux must balance the output flux (A(t) = B).

The temporal variation of the volume of steel in the tundish consequently becomes (see Fig. 2)

$$\begin{array}{*{20}l} {V\left( t \right)\; = \;V_{0} \; + \;\left( {A - B} \right)t} \hfill & {t\; < \;\left( {V_{ \hbox{max} } - V_{0} } \right)/\left( {A - B} \right)} \hfill \\ {V\left( t \right)\; = \;V_{ \hbox{max} } } \hfill & {t\; \ge \;\left( {V_{ \hbox{max} } - V_{0} } \right)/\left( {A - B} \right)} \hfill \\ \end{array} .$$
(3)
Fig. 2
figure 2

Time variation of the volume occupied by the steel in the tundish, according to Eq. (2) (black continuous line) and Eq. (3) (red dashed line). The two curves are temporally shifted one with respect to the other for a better comparison

Full size image

The second first-order differential equation involves the concentration C of the element of interest.

Assuming a complete and instantaneous mixing between the old and new material in the tundish, we can write the mass balance equation (which express the variation of the concentration of the element at a given time t at the output of the tundish) as

$$C\left( {t + \Delta t} \right)V\left( {t + \Delta t} \right)\; = \;C\left( t \right)V\left( t \right) + C_{2} A\left( t \right)\Delta t - BC\left( t \right)\Delta t.$$
(4)

We can write this relation as

$$C\left( {t + \Delta t} \right)V\left( {t + \Delta t} \right) - C\left( t \right)V\left( t \right)\; = \; - \;BC\left( t \right)\Delta t + C_{2} A(t)\Delta t,$$

or, for ∆t → 0

$$\frac{\text{d}}{{{\text{d}}t}}C\left( t \right)V\left( t \right)\; = \; - \;BC\left( t \right) + C_{2} A(t).$$

An equivalent way for writing Eq. 4 is

$$V\left( t \right)\frac{\text{d}}{{{\text{d}}t}}C\left( t \right) + C\left( t \right)\frac{\text{d}}{{{\text{d}}t}}V\left( t \right)\; = \; - \;BC\left( t \right) + C_{2} A(t),$$

that must be solved with the condition C(t = 0) = C1.

Dividing by V(t), we obtain

$$\frac{\text{d}}{{{\text{d}}t}}C\left( t \right)\; = \; - \left( {\frac{1}{V\left( t \right)}\frac{\text{d}}{{{\text{d}}t}}V\left( {\text{t}} \right)\; + \;\frac{B}{V(t)}} \right) C(t)\; + \; \frac{{C_{2} A(t)}}{V(t)}.$$
(5)

In the simple case in which the input flux can be considered as constant (Eq. 3), the above equation becomes:

$$\frac{\text{d}}{{{\text{d}}t}}C\left( t \right)\; = \; - \;A \frac{{C\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right)t} \right)}}.$$
(6)

4 Improvement of the model

A more realistic model of the continuous casting process should take into consideration the possibility of an imperfect mixing of the material in the tundish. Imperfect mixing reflects in the spatial inhomogeneity of the final product. Therefore, considering the effect of imperfect mixings would help in improving the quality of the steel. Despite its roughness, we will show in the following that such a simplified stochastic model would be able to represent semi-quantitatively the experimental evidence obtained by the LIBS technique.

For representing the inhomogeneity of the material at a given position × (the product of the casting velocity and time) we can represent its section (surface area = S), perpendicular to the casting direction, using a ‘Rubik-cube’ model (see Fig. 3).

Fig. 3
figure 3

The ‘Rubik cube’ structure of the billet surface at position x

Full size image

According to this representation, the mass balance condition described by Eq. (6) can be written independently for each small cube (whose volume would be ∆S × ∆x = ∆S × v × ∆t) in the form:

$$\frac{{C\left( {t + \Delta t} \right) - C(t)}}{\Delta t}\; = \; - \;A \frac{{R\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right)t} \right)}}.$$
(7)

In practice, this (extremely rough) model assumes that the slab or billet of steel would result by the union of n = S/∆S non-interacting identical small billets, each one characterized, at the position x = v × t and in the volume ∆S × ∆x, by a homogeneous composition given by the R(t) stochastic variable.

It should be noted that in sequential casting machines, the structure of the tundish and the geometry of the strands is optimized for minimizing the inhomogeneity of the material, and a substantial homogenization also occurs in the output strand(s), so that the hypothesis of non-mixing small billets would not be realistic. Nevertheless, the model should be able to represent well, at least qualitatively, the real experimental conditions.

Assuming that the probability function of the random variable R(t) could be described as

$$P\left( {R\left( t \right)} \right)\; = \;\frac{1}{{\sqrt {2\pi } \sigma (t)}}{\text{e}}^{{ - \frac{{\left( {R(t) - C(t)} \right)^{2} }}{{2\sigma (t)^{2} }}}} ,$$
(8)

we can correlate (empirically) the width σ(t) of the probability distribution to the inhomogeneity of the material.

In a first approximation, one could in fact assume that

$$\sigma = \left| {C_{2} - C(t)} \right|\frac{A(t)\; \times \;\Delta s\; \times \;v\; \times \;\Delta t}{V(t)}.$$
(9)

This assumption satisfies the intuitive conditions that the inhomogeneity of a given element in the slab/billet, at a position x, should depend

  1. (a)

    on the absolute value of the difference between its concentration C(t) in the tundish at time t and the one in the second steel grade (C2) and

  2. (b)

    on the ratio between the input volume (A(t) × ∆s × v × ∆t) and the volume of the material in the tundish.

For modelling the inhomogeneity of the sample, Eq. (7) must be solved numerically. We describe in the next section the algorithm used for the numerical simulation.

5 Numerical simulation

The simplest way of calculating numerically the solution of Eq. (6), assuming a linear input flow as described in Eq. (3), is the direct Euler method, which approximates the derivatives with finite differences

$$\frac{{C\left( {t + \Delta t} \right) - C(t)}}{\Delta t} = - A\frac{{C\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right)t} \right)}}.$$
(10)

The value of C at time t + ∆t can be calculated on the basis of its value at time t:

$$C\left( {t + \Delta t} \right) = C\left( t \right) - A\frac{{C\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right)t} \right)}}\Delta t,$$
(11)

with the condition that C(t = 0) = C1.

We can obtain a more stable numerical solution of Eq. (6) considering the finite difference in the Euler algorithm as an approximation of the derivative calculated at the time t + ∆t/2. To improve the precision and stability of the numerical solution, therefore, we should evaluate the numerical value of the concentration that appears at the right of the equal sign at that intermediate time (leapfrog method). This approach retains the simplicity of the Euler method, while guaranteeing a more stable behaviour of the solution.

In practice, we first apply the forward Euler method for calculating the value of the concentration at time t = t + ∆t/2

$$C\left( {t + \Delta t/2} \right)\; = \;C\left( t \right)\; - \;A\frac{{C\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right) \left( {t\; + \;\frac{\Delta t}{2}} \right)} \right)}}\frac{\Delta t}{2}.$$
(12)

After that, we use this value for obtaining the value of the concentration at the time t + ∆t

$$C\left( {t + \Delta t} \right) = C\left( t \right) - A\frac{{C\left( {t + \frac{\Delta t}{2}} \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right) \left( {t + \frac{\Delta t}{2}} \right)} \right)}}\Delta t.$$
(13)

The leapfrog method gives a result that is more precise of the Euler method, with a minimum increase in the computational time. We have realized a Matlab© routine for the numerical solution of Eq. (6), using this method.

For solving Eq. (7), the same approach should be applied, considering in this case that the integration interval ∆t cannot be chosen arbitrarily. In fact, the product of the casting velocity v with ∆t, in our model, gives the spatial scale of the sample inhomogeneity.

The finite differences equation to be solved is, in this case:

$$C\left( {t + \Delta t} \right) = C\left( t \right) - A\frac{{R\left( t \right) - C_{2} }}{{\left( {V_{0} + \left( {A - B} \right)t} \right)}}\Delta t,$$
(14)

with R(t) defined by Eqs. (8) and (9) and the condition that C(t = 0) = C1.

For evaluating the variations in concentration of the element of interest along the surface perpendicular to the casting direction, at the position x = v∆t, we repeated the simulation of Eq. (14) several times, to build the histogram of the concentration C(t) and extracted the mean value and width of the resulting distribution (standard deviation).

We present in the next section the results of the simulation and their comparison with the experimental LIBS analysis.

6 Results

In the framework of the activities of the LACOMORE project, portions of a billet corresponding to the transition between two consecutive grades (Fig. 4) were analyzed using the double-pulse Laser-Induced Breakdown Spectroscopy technique [12].

Fig. 4
figure 4

The transition billet analyzed by LIBS at the positions marked in the figure

Full size image

The details of the experiment have been presented elsewhere [3], so only the main results of the experiments will be discussed here.

For each position x = v × t, 150 independent spectra were acquired on the (polished) billet outer surface, corresponding to spots of roughly 200 microns in diameter, separated by the same distance, perpendicularly to the casting direction (see Fig. 5).

Fig. 5
figure 5

Geometry of the LIBS measurements

Full size image

The quantitative analysis of the single spectra, performed with the support of an Artificial Neural Network [13], showed a very good agreement between the (spatially averaged) LIBS quantitative measurements and the results of independent analysis performed in the Chemical Laboratory of Sidenor using the Optical Emission Spectroscopy (OES) instrument ARL™ 4460 from Thermo Scientific™ [14].

LIBS measurements and the analytical techniques used, together with the comparison between Spark OES and LIBS results, were discussed in detail in [3]. We refer the reader to this paper for more details about the experimental results.

The LIBS analysis was able to follow with a good precision the transition between the compositions of the different grades, and in particular the changes in concentration of Ni and Cr due to the transition between the two grades (see Fig. 6).

Fig. 6
figure 6

Dependence on Ni (squares) and Cr (circles) spatially averaged concentration with the distance from the edge of the safety margin. The length of the error bar represents the standard deviation of the LIBS results (150 independent measurements) [3]

Full size image

The variation of the space-averaged concentration of these elements with the position in the transition billet is well represented by the numerical solution of Eq. (14), which coincides with the predictions of Eq. (6) (see Fig. 7).

Fig. 7
figure 7

Dependence on a Ni and b Cr concentration with the distance from the edge of the safety margin. Continuous line: predictions of Eqs. (6) and (14); squares: space-averaged results of LIBS analysis. The length of the error bar represents the standard deviation of the measurements [3]

Full size image

The LIBS analysis, because of its higher spatial resolution with respect to OES, has the capability of evidencing the inhomogeneity of the material at a given position; this effect cannot be modelled using Eq. (6), but Eq. (14) must be solved, instead.

For determining the dependence of the sample inhomogeneity with the position x = v × t in the transition billet, Eq. (14) was solved using 150 independent realizations. The spatial scale of the sample inhomogeneity was empirically determined by varying the ∆t parameter in the simulation, since it is assumed to be of the order of ∆x = v × ∆t. In Fig. 8, the results of the simulation for the variation of Ni concentration in the transition billet are shown (the corresponding figure for Cr is similar and is not shown here).

Fig. 8
figure 8

Dependence of the Ni concentration at different positions in the transition billet. The lines represent the results of the simulation of Eq. (14) in 150 independent realizations

Full size image

In Fig. 9, the standard deviation of the Ni concentration is shown, as a function of the position x = v × ∆t in the transition billet.

Fig. 9
figure 9

Dependence of the standard deviation of the Ni concentration in the transition billet. The continuous line represents the results of the simulation or Eq. (14) on 150 independent measurements. The points represent the experimental standard deviation measured in the LIBS experiment

Full size image

Note that the points before the 4 m position correspond to the first steel grade, before the introduction of the material corresponding to the second grade. Both theoretically and experimentally (Ref. [3]), the material can be considered as spatially homogeneous, and the experimental and theoretical standard deviation of the elemental concentrations is very small.

However, the experimental data and the theoretical analysis show that the standard deviation of the steel composition is not negligible even when the spatially averaged concentration of the elements of interest has almost reached the nominal value corresponding to the second steel grade, as evidenced also in the experimental results obtained at Sidenor plant by Laserna et al. [5]. While this is not actually a problem in current industrial practice, since an extra safety zone is purposely removed after the reach of the theoretical nominal values of the second steel grade to guarantee the homogeneity of the final product, the inhomogeneous mixing of the materials in the tundish must be considered, for improving the predictive capability of the existing theoretical model.

7 Conclusion

In spite of the roughness of the ‘Rubik cube’ model developed, the agreement between the results of numerical simulation and the results obtained in the LIBS experiment is remarkable. Of course, one should not forget that the spatial inhomogeneity is introduced in the model as an empirical parameter and, therefore, the present results, although qualitatively correct, could not be used easily transferred to other casting geometries or used for predicting the actual inhomogeneity of the sample. Nevertheless, the simple model presented in this paper evidences the importance of using an experimental strategy, as the one based on the LIBS analysis supported by an Artificial Neural Network, capable to explore very quickly and with high spatial resolution the inhomogeneity of the sample. As a result of this work, both the experimental results and the stochastic ‘Rubik cube’ model of the process evidenced that the present theoretical model of the continuous casting process has to be improved, taking into account the effect of inhomogeneous mixing of the materials in the tundish. At the same time, the results presented evidence the usefulness of LIBS for on-line determination of the boundaries of the intermixing zone, since the technique is able to determine both the average composition of the material and the standard deviations. The application of LIBS diagnostics would thus reduce the quantity of material discarded in the extra safety zone, allowing for a more efficient process, both economically and environmentally.