Trapping two types of Rayleigh particles using a focused partially coherent anomalous vortex beam

Abstract

The radiation forces of focused partially coherent anomalous vortex (AV) beams on Rayleigh particles of different refractive indices are studied theoretically and numerically. The influences of the topological charge, the beam order and coherence length on the radiation force are also discussed. It is shown that the focused partially coherent AV beam can be used to trap high index of refraction particles at the focus and to trap low index of refraction particles in the vicinity of the focus. It is also found that the radiation force can be modulated by the topological charge, the beam order and the coherence length.

1 Introduction

The technique of optical trapping is based on the force of radiation pressure from focused laser beams to significantly trap and move a wide range of particle types, including atoms, molecules and nanoparticles, without inflicting detectable optical damage [1,2,3]. Since the invention, optical trapping has been a powerful tool and successfully applied in a variety of areas of science, such as physics, chemistry and biophysical research [4,5,6]. Up to now, different types of beams have been widely studied to trap particles, such as Gaussian beam [7], Laguerre–Gaussian beam [8], Lorentz–Gaussian beam [9], cylindrical vector beam [10], elegant Hermite-cosine-Gaussian beam [11], anomalous hollow beam [12], zero-order Bessel beam [13] and anomalous vortex beam [14]. In the above studies, the incident light beams for optical traps are assumed to be fully coherent. As we know, any laser field is always partially coherent in practice [15]. Thus, it is of practical significance to investigate the trapping effect of partially coherent beams.

In the past decades, the study on the optical trapping properties of partially coherent beams has become a subject of great interest [16,17,18,19,20,21,22,23]. For example, Wang et al. [16] investigated the influence of the spatial coherence length on the trapping effect of Rayleigh dielectric sphere. Auñón et al. [17] established a theory of the averaged optical force exerted by a partially coherent light on a dipolar particle. Recently, Zhao et al. [18] proposed a new method to trap two types of particles with different indices by varying the spatial coherence of partially coherent elegant Laguerre–Gaussian beam.

Over the past several years, anomalous vortex (AV) beams have attracted extensive interest due to their unique properties and wide applications in optical manipulation and atom guiding [14, 24,25,26]. For example, Yang et al. [24] revealed that the AV beam possesses interesting novel features on propagation, i.e., the AV beam becomes an elegant Laguerre–Gaussian (ELG) beam in the far field. Moreover, it is shown that the AV beam is a general model, and the hollow Gaussian beam, the ordinary Gaussian, the Bessel–Gauss beam and the Bessel vortex beam are special cases of the AV beam. Yuan et al. [25] studied the effect of aperture on the propagation properties of AV beams. Xu et al. [26] investigated the characteristics of an AV beam through the paraxial optical system and found that the beam quality of the AV beam will become good when the beam parameters are not too large.

However, as far as we know, the trapping characteristics of focused partially coherent AV beams have not yet been investigated. This paper is devoted to the analysis of radiation force produced by focused partially coherent AV beams on Rayleigh dielectric particles with different refractive particles. The analytical expressions for the propagation of partially coherent AV beams through a paraxial ABCD optical system are derived. The effects of different beam parameters, including the coherence length, beam order and topological charge of the partially coherent AV beam, on the radiation forces are discussed. Finally, the stable trapping conditions for the partially coherent AV beams have been analyzed in detail.

2 Analytical expressions and the focusing properties of focused partially coherent AV beams through thin lens optical system

The electric field of the AV beam at z = 0 is defined as follows [24]:

$${E_{n,m}}({\rho _0},{\theta _0})={E_0}{\left( {\frac{{{\rho _0}}}{{{\omega _0}}}} \right)^{2n+\left| m \right|}}\exp \left( { - \frac{{\rho _{0}^{2}}}{{\omega _{0}^{2}}}} \right)\exp ( - im{\theta _0}),$$

(1)

where E₀ is a constant, and n and m indicate the beam order and the topological charge, respectively. ω₀ is the beam waist width of fundamental Gaussian beam. ρ₀ and θ₀ are the radial and the azimuthal coordinates, respectively.

It is well known that a partially coherent beam can be characterized by the cross-spectral density (CSD). The CSD of the electric field for points in the transverse plane, ρ₁ and ρ₂, can be written as:

$$W({\rho _1},{\rho _2})=\left\langle {E({\rho _1}){E^ * }({\rho _2})} \right\rangle ,$$

(2)

where $\langle$$\rangle$ denotes an ensemble average. The asterisk stands for the complex conjugate.

Here, we assume a partially coherent light source in the initial plane with field correlation properties described by a Gaussian–Schell correlator:

$$\mu ({\varvec{\rho}_1},{\varvec{\rho}_2},0)=\exp \left( { - \frac{{{{\left| {{\varvec{\rho}_1} - {\varvec{\rho}_2}} \right|}^2}}}{{{\delta ^2}}}} \right),$$

(3)

where δ is spatial coherence length, ρ₁, ρ₂ are arbitrary points in the beam.

From Eqs. (1)–(3), the CSD of a partially coherent AV beam at the source plane z = 0 in the rectangular coordinate system is expressed as:

$$\begin{aligned} W({x_1},{y_1},{x_2},{y_2};0) & ={\left( {\frac{{x_{1}^{2}+y_{1}^{2}}}{{\omega _{0}^{2}}}} \right)^{n+\frac{m}{2}}}\exp \left( { - \frac{{x_{1}^{2}+y_{1}^{2}}}{{\omega _{0}^{2}}}} \right){(x_{1}^{2}+y_{1}^{2})^{ - \frac{m}{2}}}{({x_1}+i{y_1})^m} \\ & \quad \times {\left( {\frac{{x_{2}^{2}+y_{2}^{2}}}{{\omega _{0}^{2}}}} \right)^{n+\frac{m}{2}}}\exp \left( { - \frac{{x_{2}^{2}+y_{2}^{2}}}{{\omega _{0}^{2}}}} \right){(x_{2}^{2}+y_{2}^{2})^{ - \frac{m}{2}}}{({x_2} - i{y_2})^m} \\ & \quad \times \exp \left( { - \frac{{{{({x_1} - {x_2})}^2}+{{({y_1} - {y_2})}^2}}}{{2{\delta ^2}}}} \right). \\ \end{aligned}$$

(4)

Within the validity of the paraxial approximation, the CSD of a partially coherent AV beam after propagating in the paraxial ABCD optical system is characterized by [15]:

$$\begin{aligned} W({\rho _{1x}},{\rho _{1y}};{\rho _{2x}},{\rho _{2y}},z) & ={\left( {\frac{1}{{\lambda \left| B \right|}}} \right)^2}\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {W({x_1},{y_1},{x_2},{y_2},0)} } } } \\ & \quad \times \exp \left[ { - \frac{{ik}}{{2B}}(Ax_{1}^{2} - 2{x_1}{\rho _{1x}}+D\rho _{{1x}}^{2}) - \frac{{ik}}{{2B}}(Ay_{1}^{2} - 2{y_1}{\rho _{1y}}+D\rho _{{1y}}^{2})} \right] \\ & \quad \times \exp \left[ {\frac{{ik}}{{2B}}(Ax_{2}^{2} - 2{x_2}{\rho _{2x}}+D\rho _{{2x}}^{2})+\frac{{ik}}{{2B}}(Ay_{2}^{2} - 2{y_2}{\rho _{2y}}+D\rho _{{2y}}^{2})} \right]{\text{d}}{x_1}{\text{d}}{y_1}{\text{d}}{x_2}{\text{d}}{y_2}, \\ \end{aligned}$$

(5)

where r₁ (ρ_1x, ρ_1y) and r₂ (ρ_2x, ρ_2y) are the position vectors in the output plane and k = 2π/λ is the wavenumber with λ being the wavelength.

On substituting Eq. (4) to (5), the CSD of a partially coherent AV beam at the output plane is written as:

$$\begin{aligned} W({\rho _{1x}},{\rho _{1y}};{\rho _{2x}},{\rho _{2y}},z) & ={\left( {\frac{1}{{\lambda \left| B \right|}}} \right)^2}\frac{{{\pi ^2}}}{{{A_1}{A_2}}}{\left( {\frac{1}{{\sqrt {2{A_1}{A_2}} \omega _{0}^{2}}}} \right)^{m+2n}}{(2i)^{ - (2m+4n)}} \\ & \quad \times \exp \left( {\frac{{ - {k^2}\rho _{{1x}}^{2}}}{{4{A_1}{B^2}}}} \right)\exp \left( { - \frac{{ikD\rho _{{1x}}^{2}}}{{2B}}+\frac{{ikD\rho _{{2x}}^{2}}}{{2B}}} \right)\exp \left[ {{{\left( {\frac{{ik{\rho _{1x}}}}{{4{A_1}\sqrt {{A_2}} {\delta ^2}B}}+\frac{{ - ik{\rho _{2x}}}}{{2\sqrt {{A_2}} B}}} \right)}^2}} \right] \\ & \quad \times \exp \left( {\frac{{ - {k^2}\rho _{{1y}}^{2}}}{{4{A_1}{B^2}}}} \right)\exp \left( { - \frac{{ikD\rho _{{1y}}^{2}}}{{2B}}+\frac{{ikD\rho _{{2y}}^{2}}}{{2B}}} \right)\exp \left[ {{{\left( {\frac{{ik{\rho _{1y}}}}{{4{A_1}\sqrt {{A_2}} {\delta ^2}B}}+\frac{{ - ik{\rho _{2y}}}}{{2\sqrt {{A_2}} B}}} \right)}^2}} \right] \\ & \quad \times \sum\limits_{{{c_1}=0}}^{m} {\sum\limits_{{{c_2}=0}}^{m} {\sum\limits_{{{d_1}=0}}^{n} {\sum\limits_{{{d_2}=0}}^{n} {\sum\limits_{{{p_1}=0}}^{{m - {c_1}+2n - 2{d_1}}} {\sum\limits_{{{q_1}=0}}^{{\frac{{{p_1}}}{2}}} {\sum\limits_{{{p_2}=0}}^{{{c_1}+2{d_1}}} {\sum\limits_{{{q_2}=0}}^{{\frac{{{p_2}}}{2}}} {{i^{{c_1}+{c_2}}}\frac{{\left( {m - {c_1}+2n - 2{d_1}} \right)!}}{{{p_1}!\left( {m - {c_1}+2n - 2{d_1} - {p_1}} \right)!}}} } } } } } } \frac{{({c_1}+2{d_1})!}}{{{p_2}!({c_1}+2{d_1} - {p_2})!}}} \\ & \quad \times {( - 1)^{{c_2}+{q_1}+{q_2}}}\frac{{m!}}{{{c_1}!(m - {c_1})!}}\frac{{m!}}{{{c_2}!(m - {c_2})!}}\frac{{n!}}{{{d_1}!(n - {d_1})!}}\frac{{n!}}{{{d_2}!(n - {d_2})!}}\frac{{{p_1}!}}{{{q_1}!(p - 2{q_1})!}}\frac{{{p_2}!}}{{{q_2}!({p_2} - 2{q_2})!}} \\ & \quad \times {\left( {\frac{1}{{\sqrt {2{A_1}{A_2}} {\delta ^2}}}} \right)^{{p_1}+{p_2} - 2{q_1} - 2{q_2}}}{H_{m - {c_1}+2n - 2{d_1} - {p_1}}}\left( {\frac{{ - k{\rho _{1x}}}}{{\sqrt {2{A_1}} B}}} \right){H_{m - {c_2}+2n - 2{d_2}+{p_1} - 2{q_1}}}\left( {\frac{{ - k{\rho _{1x}}}}{{4{A_1}\sqrt {{A_2}} {\delta ^2}B}}+\frac{{k{\rho _{2x}}}}{{2\sqrt {{A_2}} B}}} \right) \\ & \quad \times {H_{{c_1}+2{d_1} - {p_2}}}\left( {\frac{{ - k{\rho _{1y}}}}{{\sqrt {2{A_1}} B}}} \right){H_{{c_2}+2{d_2}+{p_2} - 2{q_2}}}\left( {\frac{{ - k{\rho _{1y}}}}{{4{A_1}\sqrt {{A_2}} {\delta ^2}B}}+\frac{{k{\rho _{2y}}}}{{2\sqrt {{A_2}} B}}} \right), \\ \end{aligned}$$

(6)

with

$${A_1}=\frac{1}{{\omega _{0}^{2}}}+\frac{1}{{2{\delta ^2}}}+\frac{{ikA}}{{2B}},$$

(6a)

$${A_2}=\frac{1}{{\omega _{0}^{2}}}+\frac{1}{{2{\delta ^2}}} - \frac{{ikA}}{{2B}} - \frac{1}{{4{A_1}{\delta ^4}}}.$$

(6b)

The intensity distribution of a partially coherent AV beam at the output plane is given by:

$$I({\rho _{1x}},{\rho _{1y}})=W({\rho _{1x}},{\rho _{1y}};{\rho _{1x}},{\rho _{1y}},z).$$

(7)

In the above derivations, we have used the following integral formulas [27, 28]:

$$\int\limits_{{-\infty }}^{\infty } {{\alpha ^n}\exp [ - {{(\alpha - \beta )}^2}]} {\text{d}}\alpha ={(2i)^{ - n}}\sqrt \pi {H_n}(i\beta ),$$

(8)

$${H_n}(\alpha +\beta )=\frac{1}{{{2^{n/2}}}}\sum\limits_{{m=0}}^{n} {\left( {\begin{array}{*{20}{c}} n \\ m \end{array}} \right){H_m}(\sqrt 2 \alpha ){H_{n - m}}(\sqrt 2 \beta )} ,$$

(9)

$${H_n}(\alpha )=\sum\limits_{{m=0}}^{{n/2}} {{{( - 1)}^m}} \frac{{n!}}{{m!(n - 2m)!}}{(2\alpha )^{n - 2m}},$$

(10)

$${({x_1}+i{y_1})^m}=\sum\limits_{{p=0}}^{m} {\frac{{m!{i^p}}}{{p!(m - p)!}}} {x_1}^{{m - p}}{y_1}^{p}.$$

(11)

Considering the propagation of the partially coherent AV beam through a lens system, where f is the focus length of the thin lens, Δz is the axial distance between the geometrical focus plane and the output plane and the output plane is located at z = f + Δz, the ABCD matrix for the system is:

$$\left( {\begin{array}{*{20}{c}} A&B \\ C&D \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {{{ - \Delta z} \mathord{\left/ {\vphantom {{ - \Delta z} f}} \right. \kern-0pt} f}}&{f+\Delta z} \\ {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} f}} \right. \kern-0pt} f}}&1 \end{array}} \right).$$

(12)

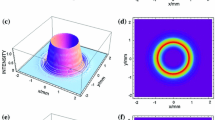
We choose the following parameters: λ = 632.8 nm, f = 5 mm, ω₀ = 10 mm, the laser beam power P = 1 W. Substituting Eq. (12) into Eqs. (6) and (7), we calculate in Fig. 1 the evolution behavior of the intensity distribution of focused partially coherent AV beam for different values of the coherence length (δ/ω₀ = 0.2, 0.4, 1, respectively) at different propagation distances in the vicinity of the focus. One finds from Fig. 1 that the focusing properties of a partially coherent AV beam are very interesting and different from that of the fully coherent case [14]. At the focal plane, the intensity profile of the focused partially coherent AV beam is of quasi-Gaussian distribution for low coherent cases, which is because the effect of the Gaussian–Schell correlator. Furthermore, maximum intensity increases as the coherence length increases, and the width of the focused partially coherent AV beam spot becomes smaller, which means a partially coherent AV beam can be focused tighter. When the output plane is a little away from the focal plane, the intensity of focused partially coherent AV beam becomes a dark hollow profile and the maximum intensity decreases as the distance away from focal plane increases. Owing to these focusing characteristics, the focused partially coherent AV beam can be expected to trap particles with different refractive indices at different positions.

Fig. 1

Intensity distribution of partially coherent AV beams with δ = ω₀ at different distances: a Δz = 0, b Δz = 0.5 µm, c Δz = 1 µm. d Evolution of partially coherent AV beams intensity distribution for different values of δ from Δz = − 1 to Δz = 1 µm

3 Radiation force on high index of refraction particles produced by focused partially coherent AV beams at the focal plane

Now, we investigate the radiation force produced by focused partially coherent AV beams acting upon a Rayleigh particle. According to the Rayleigh scattering theory, a Rayleigh particle can be regarded as a point dipole. There are two types of radiation forces acting on a Rayleigh particle: the scattering force and the gradient force. The scattering force F_scat tends to push a Rayleigh particle out of focus and destabilize the optical trap. The scattering force can be expressed as [3]:

$${\vec {F}_{{\text{scat}}}}={{{{\vec {e}}_z}{n_m}\alpha {I_{{\text{out}}}}} \mathord{\left/ {\vphantom {{{{\vec {e}}_z}{n_m}\alpha {I_{{\text{out}}}}} c}} \right. \kern-0pt} c},$$

(13)

$$\alpha =\frac{8}{3}\pi {(ka)^4}{a^2}{\left( {\frac{{{\eta ^2} - 1}}{{{\eta ^2}+2}}} \right)^2},$$

(14)

where ${\vec {e}_z}$ is a unit vector along the beam propagation direction.η = n_p/n_m denotes the relative index, and n_p and n_m denote the refractive index of the particle and ambient, respectively. α is the cross section of radiation pressure for the interaction between the light beam and microsphere. $a$ is the radius of the Rayleigh particle. c is the speed of the light in vacuum. I_out is the optical intensity of the focused beam.

Then the gradient force F_grad is responsible for pulling a Rayleigh particle toward the center of focus. The gradient force can be expressed as [3]:

$${\vec {F}_{{\text{grad}}}}={{2\pi {n_m}\beta \nabla {I_{{\text{out}}}}} \mathord{\left/ {\vphantom {{2\pi {n_m}\beta \nabla {I_{{\text{out}}}}} c}} \right. \kern-0pt} c},$$

(15)

$$\beta ={a^3}\frac{{{\eta ^2} - 1}}{{{\eta ^2}+2}}.$$

(16)

By applying Eqs. (6), (7), (12)–(16), we can calculate the radiation force at the output plane produced by focused partially coherent AV beams. We assume n_m = 1.33, $a$ = 50 nm and the other calculation parameters are the same as in Fig. 1.

Figure 2 shows the radiation force of focused partially coherent AV beams on high index of refraction particles (n_p = 1.59) for different values of the mode orders n and m with δ = 6 mm at the focal plane. The sign of the radiation forces determines the direction of the force: for the positive F_scat, the direction of the scattering force is along the + z direction; for positive F_grad,x and F_grad,z, the direction of the gradient force is along the + x or + z direction. From Fig. 2a, b, we find that the transverse gradient force points to the focus at the focal plane. Comparing Fig. 2c, f, one can see that the longitudinal gradient force is always larger than that of the scattering force. Thus, the high index of refraction particles can be stably captured at the focus. Furthermore, we can see that the radiation forces increase as the beam order n increases or topological charge m decreases.

Fig. 2

Scattering force and gradient force produced by focused partially coherent AV beams on a Rayleigh particle with n_p = 1.59 for different mode orders n, m with δ = 6 mm at the focal plane

Figure 3 displays the influence of the coherence length of focused partially coherent AV beam with n = 1, m = 1 on the radiation forces exerted on high index of refraction Rayleigh particles at the focal plane; other calculation parameters are the same as in Fig. 2. One finds from Fig. 3 that the scattering force, transverse gradient force and the longitudinal gradient force increase as the coherence length increases. However, when the coherence length equals 20 mm, there is not a stable equilibrium point for high-index particles at the focus point. For the chosen parameters in this paper, from the numerical calculations we can see that for low coherence cases (2 mm ≤ δ ≤ 10 mm), trapping high-index particles is feasible at the focus point and the trapping stability can be enhanced by increasing the coherence length.

Fig. 3

Effect of the coherence length on the radiation forces exerted on the high index of refraction particles at the focal plane. a F_{grad, x}, b F_scat, c F_{grad, z}

4 Radiation force on low index of refraction particles produced by focused partially coherent AV beams near the focal plane

We calculate in Fig. 4 the radiation force of focused partially coherent AV beams acting on the low index of refraction particles (n_p = 1) for different values of the mode orders n and m with δ = 6 mm at the axial distance Δz = 0.5µ m, and other calculation parameters are the same as Fig. 3. It is found from Fig. 4a, b that there exists one transverse stable equilibrium point at the axial distance Δz = 0.5 µm, and the transverse gradient force decreases as the beam order n or topological charge m increases. Figure 4c, d shows that the scattering force decreases with the increment of beam order n or topological charge m. Figure 4e, f shows that the particle cannot be stably trapped along the z direction. Therefore, the focused partially coherent AV beam only can transversely trap the low index of refraction particles at the axial distance Δz = 0.5µ m.

Fig. 4

Scattering force and gradient force produced by focused partially coherent AV beams with δ = 6 mm on a Rayleigh particle with n_p = 1 for different mode orders n, m at the Δz = 0.5 µm

Figure 5 indicates the influence of the coherence length of focused partially coherent AV beam with n = 1, m = 1 on the radiation forces exerted on low index of refraction Rayleigh particles at the axial distance Δz = 0.5 µm. From Fig. 5, it can be found that the gradient force and scattering force increase with increment of the coherence length. Therefore, it is much easier to trap low index of refraction particles to z-axis as for the larger coherence length.

Fig. 5

Effect of the coherence length on the radiation forces exerted on the low index of refraction particles at the axial distance Δz = 0.5 µm. a F_{grad, x}, b F_scat, c F_{grad, z}

5 Analysis of trapping stability

It is well known that the small particle usually suffers from the Brownian motion due to the thermal fluctuation from the ambient. According to fluctuation and dissipation theorem, the Brownian force is defined as [29]:

$$\left| {{F_{\text{B}}}} \right|={(12\pi \kappa a{k_{\text{B}}}T)^{1/2}},$$

(17)

where κ is viscosity of the medium, at T = 300 K, k_B is the Boltzmann constant, $a$ is the radius of the particle.

Then we obtain the Brownian force to be F_B = 2.5 × 10⁻³ pN. On comparing this value with the scattering and gradient forces in Figs. 2, 3, 4 and 5, one can find that both the gradient force and the scattering force are much larger than the Brownian force. Thus, the high-refractive index particle can be stably trapped at the focus plane, and the low-refractive index particle can be transversely trapped at the axial distance Δz = 0.5µ m.

6 Conclusion

In this paper, we have derived the analytical expressions of a partially coherent AV beam through the optical system, and have numerically and theoretically studied the radiation force acting on Rayleigh particles with different refractive indices. It has been found that a partially coherent AV beam can be used to trap the high index of refraction particles at the focal plane, and transversely capture the low index of refraction particles nearby the focal plane. Moreover, the radiation forces acting on the particles depend on the topological charge, the beam order and the coherence length. Finally, the trapping stability is also analyzed. This is of great importance for applications of the partially coherent anomalous vortex beam in the field of optical tweezers.