Virtual wavefront calibration method based on ray tracing for alignment error compensation in the interferometric bearing ball measurement system

Abstract

The accuracy of laser interferometry for measuring bearing balls is limited because it is challenging to realize null positioning of the ball being assessed. Even a slight alignment error causes the reflected wavefront to carry an uncertain aberration, which results in the surface error being obscured by the wavefront aberration. To effectively separate the surface error from the reflected wavefront, a virtual wavefront calibration method of ray tracing for alignment error compensation in the interferometric bearing ball measurement system is proposed. A virtual wavefront measurement model with variable alignment vector of the system is established based on the ray tracing principle and coordinate transform theory. According to the virtual wavefront, a calibration process is achieved in the virtual model with a known regularization and optimization method; as a result, no accurate adjustment mechanism is required to adjust the position of the bearing ball in the actual measurement system. Simulation and experiment results indicate that the proposed method is effective, and the repeatability of this measurement system is better than λ/40 peak–valley value. The final results may promote the application of this method in other fields of optical measurement.

1 Introduction

High-precision ball bearings are widely used in the aerospace, airline, transportation and manufacturing industries, such as in aircraft engine rotor system, high-speed railway vehicle, machine tool spindle components and so on. The ball bearings must operate at very high speeds and endure high radial and thrust loads; thus, it is necessary to ensure the high precision of these bearing balls, including ultrasonic and magnetic testing for inner flaws, chemical etching to find grinding burns and measurement of surface [1, 2].

The surface measurement of bearing balls is a kind of sphericity measurement. Precise measurement methods for spheres include contact measurements and non-contact measurements [3]. Contact measurements, such as the use of a three-coordinate measuring machine and the use of a profilometer, are direct and absolute; however, they are prone to causing secondary damage to the measured surface. By contrast, laser interferometry is a rapid, non-contact test method with high precision and high sensitivity that is based on the wavelength of the laser source and dose no damage to the measured surface. The precise interferometric measurement system is based on dual-beam interferometry [4, 5]. The reference wavefront reflected from the standard mirror interferes with the measurement wavefront reflected from the target surface, which includes the surface error, alignment error and other environmental information [6]. The phase information of the surface under test can be extracted from the interference images and then the surface error can be obtained [7].

With the development of metrology, the measurement accuracy of laser interferometry has gradually increased [8, 9]. Accurate measurements can be achieved on the condition that the target is precisely aligned in the null position [10]. However, in actual measurement, the null position is inconvenient and not easily achieved. Alignment error limits the accuracy of an interferometer measurement system. In general, measurement using an interferometer is an indirect method that depends on the optical path difference between the reflected wavefronts. Even a slight misalignment will lead to retracing error [6]; as a result, an obvious wavefront aberration is added, and this incident aberration cannot be distinguished from the aberration introduced by surface error. Therefore, it is critical to eliminate the misalignment aberration of the bearing ball to improve the performance of interferometry.

A number of studies have investigated the alignment error of interferometry. The traditional method of eliminating alignment error is to use a camera as an on-line aided monitor [11]. With a precision 6° adjustment mechanism, a calibration process is performed to make the interferometric fringe of the system approximately zero through real-time monitoring. In actual application of bearing ball measurement, the adjustment mechanism is simplified to 3 degrees of freedom for the symmetry of the ball, but this process is still time consuming and it exhibits residual wavefront aberration (RWA) when the fringe is not strictly zero. A misalignment sensitivity matrix (MSM) method is utilized based on an established analytical relationship between the alignment error and the wavefront to perform calibration process [12, 13]. Regarding the random alignment error, in some cases, it is impossible to describe the relationship analytically. Moreover, an approximate process of simplifying the relationship from non-linear system has been performed, and the method is effective when the alignment error is small. Lower-order Zernike coefficients of the RWA analysis have been applied to separate the aberration caused by different kinds of alignment errors [14]. However, directly removing the lower-order Zernike coefficients causes a part of the surface error to be eliminated, which often has greater influence on the measured result than the aberration brought in by the alignment error.

In this paper, we concentrate on the calibration of the alignment error in bearing ball surface measurement with Twyman–Green interferometry. The limitation of a high-accuracy measurement is that an uncertain alignment error occurs in the measurement process that cannot be easily separated from the reflected wavefront. To analyze the alignment error, first, we establish the theoretical model of the measurement system. A computational measurement model based on ray tracing is constructed to analyze the reflected wavefront of the system. In order to reserve the high-spatial frequencies of the surface error, we use wavefront data instead of polynomial fitting of the wavefront. Next, we propose the VWC method of ray tracing based on the model with variable alignment vectors to achieve a calibration process. The reverse optimization is applied to match the alignment error of the experimental wavefront and the virtual wavefront in the model. After compensating the alignment error, the surface error can be calculated even if the bearing ball being assessed is not well positioned. Simulations and experiments were performed to confirm that the proposed method is feasible and repeatable for practical application. Thus, the Twyman–Green interferometry system in combination with method of alignment error is a suitable candidate for the high-accuracy surface measurement of bearing balls and other spherical surfaces.

Section 2 describes the interferometric bearing ball measurement system based on Twyman–Green interferometry. The alignment error in various positions is also discussed in detail. In Sect. 3, the principle of the VWC method is proposed including computational measurement model, alignment vectors and reverse optimization process. Then measurement simulations and experiments of a bearing ball in different misaligned positions are presented in Sects. 4 and 5. Finally, a conclusion is drawn in Sect. 6.

2 Principle and alignment error of the interferometric bearing ball measurement system

2.1 Basic principle

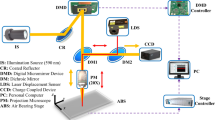
The bearing ball measurement system is based on phase shifting interferometry (PSI) [5]. Figure 1 shows a schematic diagram of the proposed system. A Twyman–Green setup is employed in this system, including the laser source, the detector and the interferometer. The laser source is a frequency-stabilized laser, and a charge-coupled device (CCD) camera is introduced as the detector to capture a series of digitized-intensity images with each phase-shifting step. The interferometer includes the collimation, the reference part and the measurement part. A beam from the laser passes through a spatial filter and a beam expander to obtain a collimated beam. After passing through a beam splitter (BS), the beam is divided into two parts. One is the reference beam, which is reflected from the reference mirror, and the other is the measurement beam, which is reflected from the surface of the bearing ball after passing through a plano-convex lens (PCL). The two beams produce interference and are imaged onto the detector by the CCD camera. The PSI is applied by moving the reference mirror with piezoelectric (PZT) actuators. With the different positions of the reference mirror, a series of interferometric images is obtained to determine the phase of the wavefront.

Fig. 1

The schematic diagram of the interferometric bearing ball measurement system

The intensity $I(x,y)$ recorded by CCD of each pixel $(x,y)$ on the interference image can be expressed as:

$$I(x,y)={I_{\text{r}}}(x,y)+{I_{\text{m}}}(x,y)+2\sqrt {{I_{\text{r}}}(x,y) \cdot {I_{\text{m}}}(x,y)} \phi (x,y),$$

(1)

where $\phi (x,y)={\phi _{\text{r}}}(x,y) - {\phi _{\text{m}}}(x,y)$; ${\phi _{\text{r}}}(x,y)$ and ${\phi _{\text{m}}}(x,y)$ are the phases of the reference and measurement beams, respectively; and ${I_{\text{r}}}(x,y)$ and ${I_{\text{m}}}(x,y)$ are the intensities of the reference and measurement beams, respectively.

Based on PSI, at least a three-step movement of the reference mirror is required. Setting three-step phase shifts as − $\sigma$, 0 and $\sigma$, $\phi \left( {x,y} \right)$ yields the following:

$$\phi (x,y)=\arctan \left( {\frac{{1 - os\sigma }}{{\sin \sigma }} \cdot \frac{{{I_1}(x,y) - {I_3}(x,y)}}{{2{I_2}(x,y) - {I_1}(x,y) - {I_3}(x,y)}}} \right),$$

(2)

where ${I_1}(x,y)$, ${I_2}(x,y)$ and ${I_3}(x,y)$ represent the intensities of the interference images from each phase-shifting step. The solution to the equations is raw phase data. To remove the 2π discontinuities in the raw phase data, the process of phase unwrapping is introduced. In the interferometric bearing ball measurement system, the path-independent method [15, 16] is employed to solve the unwrapped phase.

In the ideal case, there is no alignment error, and the null testing condition is available. The reflected wavefront ${W_{{\text{SE}}}}$ caused by surface error consists of the phase $\phi \left( {x,y} \right)$ of each single point on the premise that the spatial dependence $\left( {x,y} \right)$ of each item is omitted for conciseness. The surface error of the bearing ball under test can be expressed as:

$${E_{\text{S}}}=\frac{{{W_{{\text{SE}}}}}}{{2\pi }} \cdot \frac{\lambda }{2} \cdot \frac{1}{{{n_0}}}=\frac{{{W_{{\text{SE}}}}}}{{4\pi {n_0}}} \cdot \lambda ,$$

(3)

where ${n_0}$ is the refractive index of the air, and $\lambda$ is the wavelength of laser source.

2.2 Alignment error analysis

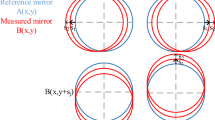
Theoretically correct but not accurate in actual measurement, the above system does not take into account the alignment errors [17, 18]. When the ball being assessed is not exactly adjusted in the theoretical position of the bearing ball measurement system, the reflected wavefront will contain an uncertain aberration caused by alignment error. In general, the alignment error of the surface under test has six degrees of freedom, while in the bearing ball measurement three degrees of freedom is participated in alignment error calibration for the symmetry of the sphere. Alignment error will cause the null condition to break down and result in retracing error [18]. Figure 2 shows the alignment error of different conditions.

Fig. 2

Spatial position under a the null testing condition; b–d translational misalignment in single axis, x-axis, y-axis, and z-axis, respectively; e translational misalignment in three axis. Simulation interference images under f the null testing condition; g–i translational misalignment in single axis, x-axis, y-axis, and z-axis, respectively; j translational misalignment in three axis

The surface error of the bearing ball under test is usually constructed from the test wavefront as:

$${W_{{\text{SE}}}}=f({W_{\text{R}}}),$$

(4)

where ${W_{\text{R}}}$ refers to the test wavefront obtained in the actual experiment. In the ideal case, the null condition can be achieved and the interference fringe is only affected by the surface error. The retrace errors exist if the surface departs from the nominal form even with perfect alignment, however they typically will be relatively small compared to the misalignment error. ${W_{{\text{SE}}}}$ is equal to ${W_{\text{R}}}$, ignoring system error and environmental error. ${E_{\text{S}}}$ is easily calculated from Eq. (3). However, a certain alignment error occurs during measurement and breaks down the null condition in general. The traditional method usually employs an accurate adjustment mechanism to reach a relatively accurate position; however, RWA remains when the fringe is not strictly zero. The aberration caused by alignment error limits the application of the measurement system with laser interferometry in the precision measurement.

3 VWC method of ray tracing for alignment error compensation

3.1 VWC method of ray tracing

To analyze the aberration caused by alignment error, we propose the VWC method of ray tracing based on the computational optic model of the measurement system with alignment vector.

An accurate surface error can be obtained only when the alignment error is calibrated. The virtual wavefront system of ray tracing is a numerical wavefront [19] interferometer aimed at approaching the condition of the real interferometer. Therefore, our work is to ensure that the alignment errors of these two interferometers are as close as possible.

In general, the possible misalignments of the surface under test are illustrated in Fig. 3. The surface may suffer unwanted misalignments corresponding to six basic degrees of freedom in 3D Cartesian space. We set the three translational degrees of freedom as $a$, $b$ and $c$ and the three rotational degrees of freedom as $\alpha$,$\beta$, and $\gamma$.

Fig. 3

Geometric model of the measurement system with alignment vector

These six parameters of alignment error define the alignment vector $\Delta$.

$$\Delta =[a,b,c,\alpha ,\beta ,\gamma ].$$

(5)

Assuming that the test surface in theoretical position moves to a random position, we obtain a certain vector $\Delta$ to express the movement. Thus, we have a new point $P'\left( {x',y',z'} \right)$ of the surface under test from the original point $P\left( {x,y,z} \right)$ of the theoretical coordinate system with four coordinate transformation matrices:

$${R_{12}}=\left[ {\begin{array}{*{20}{c}} 1&0&0&a \\ 0&1&0&b \\ 0&0&1&{{f_{{\text{pc}}}}+c} \\ 0&0&0&1 \end{array}} \right],$$

(6)

$${R_{23}}=\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos \alpha }&0&{\sin \alpha } \\ 0&{ - \sin \alpha }&1&{\cos \alpha } \\ 0&0&0&1 \end{array}} \right],$$

(7)

$${R_{34}}=\left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta }&0 \\ 0&1&0&0 \\ {\sin \beta }&0&{\cos \beta }&0 \\ 0&0&0&1 \end{array}} \right],$$

(8)

$${R_{45}}=\left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma }&0&0 \\ { - \sin \gamma }&{\cos \gamma }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right],$$

(9)

$$\left[ {\begin{array}{*{20}{c}} {x'} \\ {y'} \\ {z'} \\ 1 \end{array}} \right]={R_{45}}{R_{34}}{R_{23}}{R_{12}}\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \\ 1 \end{array}} \right]=F(\Delta )\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \\ 1 \end{array}} \right],$$

(10)

where ${f_{{\text{pc}}}}$ is the focus length of the PCL. $F(\Delta )={R_{45}}{R_{34}}{R_{23}}{R_{12}}$ is taken as the alignment variate function (AVF) of the virtual wavefront system. With AVF, the surface equation is confirmed as $G(\Delta )=0$. Because of the rotational symmetry of the sphere, the geometric model of the measurement system of bearing ball simplifies to 3° and AVF is only influenced by ${R_{12}}$.

3.2 Alignment error compensation using the VWC method

In the traditional method, the misalignments are adjusted by employing precise adjusting mechanism or manual operation. Nevertheless, the calibration process is still troublesome and time consuming [20, 21]. Furthermore, RWA remains when the fringe is not zero. Therefore, we propose the VWC method of ray tracing instead of actual adjustment misalignment.

First, we obtain test wavefront ${W_{\text{R}}}$ in the actual experiment with the bearing ball measurement system. ${W_{\text{R}}}$ can be expressed as:

$${W_{\text{R}}}={W_{\text{S}}}+{W_{{\text{AE}}}}+{W_{{\text{SE}}}},$$

(11)

where ${W_{\text{S}}}$ refers to the wavefront aberration of the system error and the environmental error, ${W_{{\text{AE}}}}$ refers to the wavefront aberration of the alignment error, and ${W_{{\text{SE}}}}$ refers to the wavefront aberration of surface error, which is the measurement target of interest.

In the proposed system, ${W_{\text{S}}}$ can be obtained by the measurement of a standard reflector in place of the test arm. After compensating the effect of ${W_{\text{S}}}$, we obtain ${W_{\text{R}}}'$, which is only influenced by ${W_{{\text{AE}}}}$ and ${W_{{\text{SE}}}}$:

$${W_{\text{R}}}'={W_{{\text{AE}}}}+{W_{{\text{SE}}}}.$$

(12)

${W_{{\text{AE}}}}$ changes the shape of ${W_{\text{R}}}^{\prime }$ and influences the values of PV and root-mean-square (RMS) of the surface. The calibration process is aimed at eliminating the influence of ${W_{{\text{AE}}}}$ upon the measurement result.

Next, we obtain the virtual numeric wavefront ${W_{\text{U}}}$ with the virtual wavefront system. According to AVF, $G(\Delta )$ including alignment vector $\Delta$ is obtained. ${W_{\text{U}}}$ is a virtual wavefront without any surface error. Thus, we have:

$${W_{\text{U}}}(G(\Delta ))={W_{{\text{UAE}}}}(G(\Delta )),$$

(13)

where the wavefront ${W_{{\text{UAE}}}}$ is influenced only by the alignment error.

The VWC method is adopted to estimate the difference between the virtual wavefront and the actual wavefront. If we find the alignment vector $\Delta$ to make ${W_{{\text{UAE}}}}(G(\Delta ))={W_{{\text{AE}}}}$, then we will have:

$${W_{{\text{SE}}}}={W_{\text{R}}}' - {W_{{\text{UAE}}}}(G(\Delta ))$$

(14)

Thus, the purpose of the virtual wavefront system is to adjust the alignment vector $\Delta$ to make the alignment error in the virtual model equal to that of the actual experiment. Under these circumstances, ${W_{{\text{SE}}}}$ can be solved correctly, even if, in the actual experiment, the surface is still misaligned.

Since the change of alignment vector $\Delta$ can be performed in the virtual wavefront system, it can be considered as an optimization problem. Alignment error has a more significant influence on the test wavefront than surface error [12]; therefore, ${W_{\text{R}}}'$ is employed for the optimization process. Mathematically,

$$\varepsilon (\Delta )={W_{\text{R}}}' - {W_{{\text{UAE}}}}(\Delta ).$$

(15)

In the measuring system, the wavefront ${W_{\text{R}}}'$ is written in matrix form as follows:

$${W_{\text{R}}}'=\left[ {\begin{array}{*{20}{c}} {{R_{11}}}&{{R_{12}}}& \cdots &{{R_{1n}}} \\ {{R_{21}}}&{{R_{22}}}& \cdots &{{R_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{R_{m1}}}&{{R_{m2}}}& \cdots &{{R_{mn}}} \end{array}} \right],$$

(16)

where $m$ and $n$ refer to the number of pixels of the tested wavefront.

Correspondingly, ${W_{{\text{UAE}}}}(\Delta )$ can be written as:

$${W_{{\text{UAE}}}}(\Delta )=\left[ {\begin{array}{*{20}{c}} {{U_{11}}(\Delta )}&{{U_{12}}(\Delta )}& \cdots &{{U_{1n}}(\Delta )} \\ {{U_{21}}(\Delta )}&{{U_{22}}(\Delta )}& \cdots &{{U_{2n}}(\Delta )} \\ \vdots & \vdots & \ddots & \vdots \\ {{U_{m1}}(\Delta )}&{{U_{m2}}(\Delta )}& \cdots &{{U_{mn}}(\Delta )} \end{array}} \right].$$

(17)

Here, we introduce mathematical symbols to analyze the optimization problem. The coefficient of determination ${W_{{\text{RS}}}}$ can be defined as:

$${W_{{\text{RS}}}}=\frac{{\sum\nolimits_{{i=1}}^{m} {\sum\nolimits_{{j=1}}^{n} {{{({U_{ij}}(\Delta ) - \bar {R})}^2}} } }}{{\sum\nolimits_{{i=1}}^{m} {\sum\nolimits_{{j=1}}^{n} {{{({R_{ij}} - \bar {R})}^2}} } }},$$

(18)

where $\bar {R}$ refers to the average value of ${R_{ij}}$. Optimization of the objective function can be defined as:

$$\chi (\Delta )=\hbox{min} {({W_{{\text{RS}}}} - 1)^2}.$$

(19)

By solving optimization $\chi (\Delta )$ with a known regularization and optimization method, we obtain the alignment vector $\Delta$ that describes the actual measurement system; thus, the location of simulated virtual wavefront is consistent with the location in actual experiment. This process is much easier than the actual adjustment in the experiment. Thus, the ${W_{{\text{UAE}}}}(G(\Delta ))$ is obtained, and ${W_{{\text{SE}}}}$ can be solved correctly.

4 Simulations

The VWC method was conducted in a simulated measurement for a bearing ball with a diameter of 40 mm, whose actual surface errors are 0.2702λ (PV) and 0.0199λ (RMS). The PLC with a radius of 13.1 mm is employed, whose thickness and refractive index are 11.7 mm and 1.515497 at the wavelength λ = 632.8 nm, respectively.

In this simulation, the bearing ball measurement system of laser interferometry was modeled according to these parameters above in ray tracing model, serving as the actual experiment system with a certain alignment error to obtain interference images. With these images, we can easily calculate the wavefront data ${W_{\text{R}}}'$ while ignoring the system error and environmental error. Subsequently, the numerical wavefront was simulated using the VWC method. With the iterative optimization process for the alignment vector $\Delta$, ${W_{{\text{SE}}}}$ can be solved after alignment error compensation. The result is shown in Fig. 4. Figure 4a shows one of the interference images from the simulated measurement. Figure 4b, c shows the 2D surface error map without and with the proposed calibration method, respectively; their PV values are 3.1628λ and 0.2713λ, respectively. Without calibrating the alignment error, the surface error is obscured by the wavefront aberration caused by disalignment. The surface error of the PV value without calibration has been amplified nearly 12-fold. Figure 4d is the actual surface error of the simulation and Fig. 4e is the residual error of Fig. 4d. The difference of PV between Fig. 4c and Fig. 4d is 0.0011λ.

Fig. 4

The simulation result. a Simulation interference image. b Surface error without calibration. c Surface error with the VWC method. d Actual surface error. e Residual error of c

The repeatability simulation results of an identical location are presented to verify the stability of the VWC method. The results are shown in Table 1. The maximum differences of the PV and RMS values between the simulation results and the actual surface error are approximately 0.0124λ and 0.0074λ, respectively.

Table 1 The simulation results of an identical location

The three independent simulations with different disalignment of the bearing ball were conducted based on the VWC method, defined as Sim. A, B and C, respectively. After calibration, the alignment error of the three simulations were compensated and the spatial displacement is shown in Table 2.

Table 2 The spatial displacement in the three independent simulations with different locations

Figure 5 shows the solved surface error of the three simulations. The PV values of them are 0.2799λ, 0.2679λ and 0.2742λ, while RMS values are 0.0232λ, 0.0188λ and 0.0220λ, respectively. The maximum differences of the PV and RMS values between the simulation results and the actual surface error are approximately 0.012λ and 0.0044λ, respectively.

Fig. 5

The solved surface errors of a Sim. A, b Sim. B and c Sim. C as obtained with the VWC method

5 Experiments and results

The interferometric bearing ball measurement system at the wavelength of 632.8 nm shown in Fig. 6 was set up to confirm the validity of the VWC method. The measurement system consists of three parts: He–Ne laser source, collimation part and interferometer part. The laser source is a frequency-stabilized He–Ne laser (LE-LS-633-2.0NA) with a central wavelength of 632.8 nm and a beam diameter of 1.18 mm. The collimation part is composed of a spatial filter aimed at obtaining a better collimation plane wavefront instead of a Gaussian plane-wave. The interferometer part is primarily a Twyman–Green interferometer, including a beam expander, a CCD camera, a reference mirror with PZT and the bearing ball being assessed.

Fig. 6

The interferometric bearing ball measurement system

In this experiment, we take a bearing ball with a radius of 20 mm as the target. The parameters of the PCL are the same as those in the simulation.

The first step was to establish the optical geometric model of the measurement system. With the VWC method, ${W_{{\text{UAE}}}}(G(\Delta ))$ with variable alignment vector $\Delta$ was obtained. Moreover, ${W_{\text{S}}}$ was solved by the measurement of a standard reflector. Subsequently, the bearing ball was assessed using the measurement system, and then ${W_{\text{R}}}'$ was calculated from the interference images with the PSI method according to Eq. (2). Thus, we set the $\hbox{min} {\left| {\chi (\Delta )} \right|^2}$ as an objective function; the end condition of this optimization was a $\chi (\Delta )$ less than 0.005λ. After the optimization process, $\Delta$ was found, and ${W_{{\text{UAE}}}}(G(\Delta ))$ was removed from ${W_{\text{R}}}'$. Finally, the calibration process was performed and ${E_{\text{S}}}$ was calculated according to Eq. (3). The measurement result is shown in Fig. 7. Figure 7a is one of the interference images captured from the CCD camera in actual measurement. Figure 7b, c are 2D maps of the PV value with and without the VWC method, respectively, and the PV values are 6.2650λ and 0.6301λ, respectively. Clearly, without compensation based on the VWC method, the surface error is obscured by the wavefront alignment error.

Fig. 7

The measurement result. a Interference image. b Surface error without calibration. c Surface error with the VWC method

The result of repeatability measurements in the proposed measurement system is presented to verify the stability of the VWC method. The ten independent experimental results with an identical location of the bearing ball indicate that the VWC method could achieve measurement repeatability of λ/60 (PV) and λ/100 (RMS), even if the bearing ball is not well aligned. The experimental results are shown in Table 3.

Table 3 The measurement results in the ten independent experiments with an identical location of the bearing ball

Next, three experiments with different locations were conducted as Exp. A, B and C, respectively. The alignment error of the three experiments were compensated based on VCW method and the spatial displacement is shown in Table 4.

Table 4 The spatial displacement in the three independent experiments with different locations

Figure 8 shows the interference images and the measurement results of the three different positions of the bearing ball. The PV values of these three experiments are 0.6343λ, 0.6374λ and 0.6587λ, and their RMS values are 0.0275λ, 0.0203λ and 0.0329λ, respectively. When the ball position adjustment changes, the interference images change at the same time. With the VWC method, the measurement results remain at a stable level. The maximum deviations of the PV and RMS values are 0.0244λ and 0.0126λ, respectively. In summary, the experimental results are consistent with the simulation results, indicating that the repeatability of the VWC method is approximately λ/40 (PV) or λ/80 (RMS).

Fig. 8

Measurement results of Exp. A, Exp. B and Exp. C, respectively. a–c Interference images and d–f solved surface errors as obtained with the VWC method

The VWC method with variable alignment vectors is demonstrated to be an effective method for implementing the bearing ball measurement system with laser interferometry. The repeatability of the surface error of a fixed but misaligned bearing ball is better than λ/60 (PV) and λ/100 (RMS). When the ball under test is moved to different locations, the maximum deviation is λ/40 (PV) and λ/80 (RMS). Error sources in the proposed measurement system include the modeling error in the virtual wavefront system, environmental error and the residual system of the standard reflector testing, and the phase-extracting error of PSI and residual alignment error caused by phase compensation with surface error after calibration. The residue error of the standard reflector testing is around λ/200 (PV) after compensation of ${W_{\text{S}}}$. An estimation of approximately λ/100 (PV) can be given for the above error sources in the measurement system. The accuracy may be increased if the optimization step size is even smaller and the end condition is stricter in the algorithm. However, the accuracy is inevitably limited due to the compensation between the surface error and the alignment errors. Currently, the measurement repeatability is approximately λ/40 (PV); thus, the proposed measurement system should be adequate for other applications.

6 Conclusion

To effectively and precisely measure bearing balls without causing contact damage, a general measurement system based on Twyman–Green interferometry in combination with the VWC method is proposed. According to the PSI technology, we applied a PZT to move the reference mirror to capture a series of interference images. To obtain the unwrapped phase, we applied the path-independent method. To compensate the alignment error caused by inaccurate positioning of the bearing ball, we propose the VWC method based on ray tracing in the virtual measurement system instead of adjusting the actual system. With reverse optimization of AVF, the alignment error can be compensated. The system is highly flexible and does not require a precision adjustment mechanism. The results show that the proposed measurement system with laser interferometry is effective for bearing ball testing even if the ball is not well adjusted. The measurement repeatability of the VWC method is approximately λ/40 (PV). We anticipate that the proposed technique will be a promising metrological method in other fields of surface measurement.