1 Introduction

The impact of a magnetic field on an incident light can be traced back to M. Faraday’s experimental works, in which the polarization plane of the light propagating through a transparent medium undergoes a rotation proportional to the strength of magnetic field [1]. Since then, the Faraday effect has been playing an important role in diagnosing the strength of the magnetic field in many areas [2,3,4,5,6,7].

For a sufficiently strong light that exceeds the ionization threshold of the medium, the components of the medium are dynamically varying with the electric strength, which means the time-varying refractive index. For example, as an intense laser pulse is focused on a dilute gaseous medium, the leading edge of the laser pulse propagates in the almost neutral medium, while the trailing edge travels in the partially ionized plasma. In the presence of an axial strong magnetic field, the direction of the laser electric field experiences time-dependent rotations [8].

In many practical applications, the magnetic field is not in the direction of the laser propagation. For example, in indirect inertial confinement fusion, an axial strong magnetic field is used to improve the laser-coupling in hohlraum plasma, in which the laser beams are focused on the hohlraum wall in some specific directions. During the interaction of an ultra-intense laser pulse with a solid or plasma medium, strong magnetic fields can be generated via several mechanisms, e.g., the Biermann battery effects [9], the Weibel instability [10,11,12], the inverse Faraday effect [13, 14], the ponderomotive forces of intense laser beams [15, 16], etc. These mechanisms describe how the motion of electrons generates the electric current which is the source of the seed magnetic fields in dense plasma, and the directions of magnetic field are also complicated. Moreover, the self-generated magnetic field also has an influence on the polarizations of incident laser pulse, and consequently in turn affects the dynamics of the dense plasma.

The main purpose of this paper is to investigate the impact of a magnetic field with arbitrary direction on the polarization of the incident intense laser pulse, where the magnetic field is assumed to be constant for convenience. Figure 1 is the schematic illustration of this work. A strong pulse linearly polarized along \({\mathbf {e}}_x\)-axis propagates in a gaseous medium (Helium), and \({\mathbf {e}}_\xi\) is the propagation direction. The magnetic field \({\mathbf {B}}\) is orientated with the angles \(\theta\) and \(\phi\). From the microscopic viewpoint, a helium atom is ionized by the strong laser field, and then the ionized electron is accelerated by the laser field and the external magnetic field. Throughout this paper, the international system of units is adopted unless otherwise noted.

Fig. 1
figure 1

Schematic model of an incident laser pulse traveling through a gaseous medium in the presence of strong magnetic field whose direction is parameterized by \(\theta\) and \(\phi\). The inlet represents a microscopic process that a helium atom is ionized by the strong laser field, and then the ionized electron quivers with the magnetic field and laser electric field

Full size image

2 Theoretical model

To describe the evolution of a laser pulse propagating along \({\mathbf {z}}\)-axis, we adopt the co-moving frame with the laser pulse, \(\tau =t-z/c\) and \(\xi =z\), where t and \(\tau\) are the time variables of the laser pulse in the laboratory and co-moving frames, respectively, \(\xi\) is the propagation variable, and c the speed of light in vacuum. Using the slowly varying-envelope approximation, the propagation equation of a strong femtosecond laser pulse reads [8]

$$\begin{aligned} -\frac{2}{c}\frac{\partial ^2{\mathbf {E}}}{\partial \xi \partial \tau }=\mu _0\frac{\partial ^2{\mathbf {P}}_\mathrm{ion}}{\partial \tau ^2}+\mu _0\frac{\partial {\mathbf {J}}_\mathrm{p}}{\partial \tau }{,} \end{aligned}$$
(1)

where \(\mu _0\) is the magnetic permeability. For a short propagation distance (\(\sim 1\text { cm}\)) that is less than the Rayleigh length, the transverse diffraction can be neglected. Besides, for a dilute gaseous medium, the contribution to the polarization from the neutral atoms is not taken into consideration because it is sufficiently small compared with that from the ionized electrons [8]. It is noted that the ionization process and the acceleration of ionized electrons are treated separately, which are different from the reference [8]. The first term \({\mathbf {P}}_\mathrm{ion}\) on the right-hand side means the polarization caused by the optical field ionization. The last term (i.e., plasma current \({\mathbf {J}}_\mathrm{p}\)) accounts for plasma oscillations under the influence of external magnetic field and laser electric field.

2.1 Atomic ionization

As a response to the external electric field, the ionization process can also be regarded as a kind of extremely nonlinear polarization effects. In the classical formalism, we use the energy conservation condition during the process of ionization. In this case, the polarization caused by ionization of medium is a transient process, and the energy loss is used to release the atomic electrons:

$$\begin{aligned} d{\mathbf {P}}_\mathrm{ion}(\tau )\cdot {\mathbf {E}}(\tau )=eI_\mathrm{p} \mathrm{d}\rho _{e}(\tau ), \end{aligned}$$
(2)

where e is the electron charge, \(I_\mathrm{p}\) is the ionization potential of helium atom in unit of electron Volt (eV), and \(\mathrm{d}\rho _{e}(\tau )\) is the electron density produced within the interval \(\mathrm{d}\tau\) at \(\tau\). Supposing the polarization \(d{\mathbf {P}}_\mathrm{ion}(\tau )\) is created in the direction of \({\mathbf {E}}(\tau )\), we have

$$\begin{aligned} \frac{\partial ^2{\mathbf {P}}_\mathrm{ion}(\tau )}{\partial \tau ^2}=eI_\mathrm{p}\frac{\partial }{\partial \tau }\left[ \frac{{\mathbf {E}}(\tau )}{\left| {E}(\tau )\right| ^2}\frac{\partial \rho _{e}(\tau )}{\partial t}\right] {.} \end{aligned}$$
(3)

The electron density \(\rho _e(\tau )\) is determined by the rate equation \(\partial \rho _e(\tau )/\partial \tau =W(E)\left[ \rho _0-\rho _e(\tau )\right]\), where \(\rho _0\) is the initial density of the gaseous medium. The ionization rate W(E) depends on the ionization mechanisms parameterized by the electric strength E through \(\gamma _K=\omega _L\sqrt{2I_\mathrm{p}}/E\) (in atomic units) [17, 18], such as multiphoton ionization, tunneling ionization and over-barrier ionization, where \(\omega _L\) is the central angular frequency of the laser field.

2.2 Plasma current

The electric current caused by the laser-produced plasma is determined by \(d{\mathbf {J}}_\mathrm{p}(\tau )=e{\mathbf {v}}({\tau _0},\tau )\mathrm{d}\rho _{e}(\tau _0)\), then we have

$$\begin{aligned} {\mathbf {J}}_\mathrm{p}(\tau )=e\int ^{\tau }_{-\infty }{\mathbf {v}}(\tau ',\tau )\frac{\partial \rho _e}{\partial \tau '}\mathrm{d}\tau '{,} \end{aligned}$$
(4)

where \({\mathbf {v}}(\tau _0,\tau )\) is the velocity at \(\tau\) of electrons which are released at \(\tau _0\). The derivative of the current is obtained by differentiating Eq. (4) with respect to \(\tau\):

$$\begin{aligned} \frac{\partial {\mathbf {J}}_\mathrm{p}}{\partial \tau }=e\frac{\partial \rho _e}{\partial \tau }{\mathbf {v}}(\tau ,\tau )+e\int ^{\tau }_{-\infty }{\frac{\partial \rho _e}{\partial \tau '}\frac{\partial {\mathbf {v}}(\tau ',\tau )}{\partial \tau }}\mathrm{d}\tau '{,} \end{aligned}$$
(5)

where \({\mathbf {v}}(\tau ,\tau )\) is the initial velocity of electrons as they are released, which can be neglected compared with the time-dependent velocity gained during the acceleration. The factor \({\partial {\mathbf {v}}(\tau ',\tau )}/{\partial \tau }\) in the last term is just the acceleration of ionized electrons. When a femtosecond laser pulse propagates in dilute gaseous medium, the collisions of an electron with other electrons or atoms can be neglected. Therefore, the dynamics of an electron that is born at \(\tau _0\) is described by the Lorentz equation under the influence of strong laser electric field \({\mathbf {E}}(\tau )\) and a strong magnetic field \({\mathbf {B}}\), which reads in the matrix form,

$$\begin{aligned} \frac{\partial {\mathbf {V}}(\tau _0,\tau )}{\partial \tau }=\varOmega {\mathbf {V}}(\tau _0,\tau )+{\mathbf {A}}(\tau ) \end{aligned}$$
(6)

with

$$\begin{aligned} {\mathbf {V}}(\tau _0,\tau )&=\left[ \begin{matrix} {{v}_{x}} \\ {{v}_{y}} \\ {{v}_{\xi }} \\ \end{matrix} \right] ,\quad {\mathbf {A}}(\tau )=\frac{e}{m_e}\left[ \begin{matrix} {{E}_{x}} \\ {{E}_{y}} \\ {{E}_{\xi }} \\ \end{matrix} \right] ,\\ \varOmega&=\omega _\mathrm{c}\left[ \begin{matrix} 0 &{} {{b}_{\xi }} &{} -{{b}_{y}} \\ -{{b}_{\xi }} &{} 0 &{} {{b}_{x}} \\ {{b}_{y}} &{} -{{b}_{x}} &{} 0 \\ \end{matrix} \right] , \end{aligned}$$

where \(\omega _\mathrm{c}=eB/m_e\) is the electron cyclotron frequency in the magnetic field \(B=|{\mathbf {B}}|\), and \(b_x=\sin \theta \cos \phi ,\; b_y=\sin \theta \sin \phi\), and \(b_\xi =\cos \theta\). The collisions of the ionized electrons with their parent ions are not involved here because the electrons’ trajectories are bent greatly by the magnetic field, and the Coulomb attractions from the parent ions are also neglected.

Using the established procedure and performing some calculations, the analytical solution to Eq. (6) is obtained in the integral form as

$$\begin{aligned} {\mathbf {V}}\left( {{\tau }_{0}},\tau \right)&={\mathbf {U}}(\tau -{{\tau }_{0}}){\mathbf {V}}({{\tau }_{0}},{\tau _0})\nonumber \\&\quad +\int _{-\infty }^{\tau }{{\mathbf {U}}}(\tau -\tau '){\mathbf {A}}(\tau ')\mathrm{d}\tau ', \end{aligned}$$
(7)

where

$$\begin{aligned} {\mathbf {U}}\left( \tau \right)= & {} {{{\mathbf {Q}}}_{0}}+{{{\mathbf {Q}}}_{1}}\sin \left( {{\omega }_{c}}\tau \right) +{{{\mathbf {Q}}}_{2}}\left[ 1-\cos \left( {{\omega }_{c}}\tau \right) \right] , \\ {{{\mathbf {Q}}}_{0}}= & {} \left[ \begin{matrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{matrix} \right] ,\quad {{{\mathbf {Q}}}_{1}}=\left[ \begin{matrix} 0 &{} {{b}_{\xi }} &{} -{{b}_{y}} \\ -{{b}_{\xi }} &{} 0 &{} {{b}_{x}} \\ {{b}_{y}} &{} -{{b}_{x}} &{} 0 \\ \end{matrix} \right] , \\ {{{\mathbf {Q}}}_{2}}= & {} \left[ \begin{matrix} -b_{y}^{2}-b_{\xi }^{2} &{} {{b}_{x}}{{b}_{y}} &{} {{b}_{x}}{{b}_{\xi }} \\ {{b}_{x}}{{b}_{y}} &{} -b_{x}^{2}-b_{\xi }^{2} &{} {{b}_{y}}{{b}_{\xi }} \\ {{b}_{x}}{{b}_{\xi }} &{} {{b}_{y}}{{b}_{\xi }} &{} -b_{x}^{2}-b_{y}^{2} \\ \end{matrix} \right] . \end{aligned}$$

It shows that the Lorentz force from the magnetic field changes the electron trajectories with a frequency \(\omega _\mathrm{c}\), which makes the electrons have velocity components along the \({\mathbf {y}}\)-axis and \({\xi }\)-axis.

2.3 Propagation equation

By substituting Eqs. (3) and (5) into Eq. (1) and using Eq. (6), we can obtain the propagation equation of the laser pulse in gaseous medium. To analyze the conversion of electric field from x-component to y- and \(\xi\)-components more conveniently, we integrate the two sides over \((-\infty ,\tau ]\), and achieve the final propagation equation in integro-differential form:

$$\begin{aligned} \frac{\partial {\mathbf {E}}}{\partial \xi }=&-\frac{e\mu _0 c I_\mathrm{p} }{2}\left[ \frac{\mathbf {E(\tau )}}{\left| E(\tau )\right| ^2}\frac{\partial \rho _e}{\partial \tau }\right] -\frac{1}{2c}\int ^{\tau }_{-\infty }d\tau '\omega _\mathrm{p}^2(\tau '){\mathbf {E}}(\tau ')\nonumber \\&-\frac{e^2\mu _0 c}{2 m_e}\int ^{\tau }_{-\infty }d\tau '\left[ \int ^{\tau '}_{-\infty }{d\tau ''\frac{\partial \rho _{e}}{\partial \tau ''}{\mathbf {V}}({\tau ''},\tau ')}\times {\mathbf {B}}\right] , \end{aligned}$$
(8)

where \(\omega _\mathrm{p}(\tau )=\sqrt{{\rho _e(\tau )e^2}/({m_e\varepsilon _0})}\) is the time-dependent plasma frequency due to the time-dependent electron density \(\rho _e(\tau )\), and \(\mu _0\varepsilon _0={1}/{c^2}\) is used. The first term represents the laser energy loss due to the optical field-ionization of the gaseous medium. The second term means that the ionized electrons gain their kinetic energies from the laser field, and then drive the plasma oscillating with the time-varying frequency \(\omega _\mathrm{p}(\tau )\). The second line describes the bending of the electrons’ velocity by the external strong magnetic field, which converts the laser energy from the x-component to the y- and \(\xi\)-components, i.e., the excitation of the electric field along the \({\mathbf {y}}\)- and \({\xi }\)-axes.

3 Simulations and discussion

In our calculations, the linearly polarized laser pulse with a central wavelength \(\lambda _L=800\) nm is focused on the gaseous medium, \(\mathbf {{E}}_\mathrm{in}(\tau )={\mathbf {e}}_xE_0f(\tau )\cos (\omega _L\tau )\), where \({\mathbf {e}}_x\) is the unit vector along the \({\mathbf {x}}\)-axis, the angular frequency \(\omega _L=2\pi c/\lambda _L\). The electric strength \(E_0\) relates to the peak intensity \(I_0=\varepsilon _0cE_0^2/2\). The envelop is chosen as \(f(\tau )=\exp {\left[ -\tau ^2/\tau ^2_\mathrm{f}\right] }\), where \(\tau _f=5\text { fs}\) characterizes the pulse length.

Considering the spreading of the laser pulse in time domain, the computational time duration ranges from \(-12\) to \(40 \text { fs}\) in this work. The number of grid points for \(\tau\) is 3000, which corresponds to the grid spacing \(\varDelta \tau \approx 0.017 \text { fs}\). The laser pulse propagates for a distance of \(1.0\text { cm}\), and the fixed step size \(\varDelta \xi =0.1\upmu \text {m}\).

Figure 2(a)–(c) presents the profiles of the final electric pulse normalized by the input laser field \(E_0\), and the initial parameters are given in the caption. For the sake of comparison, the incident laser pulse is also plotted by red dashed line in (a). Clearly, the x-component of the final pulse denoted by the blue solid line exhibits significant blue-shifting and decays greatly, and spreads as a long tail on the back edge of the pulse, which is circumscribed by the black dashed rectangle. In (b) and (c), the electric field components polarized along \({\mathbf {y}}\)-axis and \({\xi }\)-axis are excited after \(\tau \sim -4\) fs (the black dashed-dotted line) with almost the same oscillation period.

Fig. 2
figure 2

The profile of the normalized output electric field at a distance of \(\xi =1\text { cm}\). a–c are the x-, y- and \(\xi\)-components of the output electric field in time domain, respectively. Here, the incident laser intensity is \(I_0=2\times 10^{15} \text {W/cm}^2\), and the external magnetic strength \(B_0=2500\) Tesla (T), \(\phi =\pi /3\), and \(\theta =\pi /6\)

Full size image

3.1 Velocity distribution of ionized electrons

According to the classical Ampére–Maxwell’s equation [19], \({\partial {\mathbf {E}}}/{\partial t}\sim {\mathbf {J}}_s/\varepsilon _0\) (the magnetic field is omitted), where the \({\mathbf {J}}_s\) is the electric current source caused by the plasma’s movement, \(\varepsilon _0\) is the dielectric constant. By taking the producing rate as weighting factors, we can define the velocity distribution of ionized electrons [20],

$$\begin{aligned} {\mathcal {P}}(\tau ,{\mathbf {V}})=\int ^\tau _{-\infty }\frac{\partial \rho _e}{\partial \tau '}\delta [{\mathbf {V}}-{\mathbf {V}}(\tau ',\tau )]\mathrm{d}\tau ', \end{aligned}$$
(9)

where \(\delta [\cdot ]\) is the Dirac function matching the velocity of ionized electrons with the coordinate reference \({\mathbf {V}}\). It is noteworthy that the distribution function satisfies the time-dependent density of ionized electrons, \(\rho _e(\tau )=\int {\mathcal {P}}({\mathbf {V}})d^3V\). In Fig. 3, we give the snapshots of velocity distributions in the \(V_Y\)–\(V_\xi\) plane at several moments for the initial laser field shown in the upper panel. From the snapshots, we can see that the velocity distribution of ionized electrons has polygon-like structure consisted of several strips. To explain this, we use the Keldysh parameter \(\gamma _K<0.8\) to characterize the significant ionization regimes since the larger electric strength corresponds to the small Keldysh parameter, which are plotted by red curves and circumvented by black rectangles. For instance, around \(\tau =-4.0\) fs, plenty of electrons begin to be released, and then are accelerated and bent according to Eq. (7) by the external magnetic field and laser field. Around \(-2.7\) fs, another ionization burst occurs (see the upper panel), and the produced electrons are also accelerated, and contribute to the velocity distribution. Therefore, there are two strips in the snapshot denoted by \(\tau =-2.14\) fs, and five strips in the snapshot denoted by \(\tau =3.32\) fs. Furthermore, with the influence of the strong magnetic field and laser field, the polygon-like structure will rotate collectively.

Fig. 3
figure 3

Snapshots of the velocity distributions at several moments. Here, the parameters are the same as that used in Fig. 2

Full size image

To reveal the mechanism of generation of electric field along \({\mathbf {y}}\)- and \(\xi\)-directions, we calculate the time-dependent average electric currents

$$\begin{aligned} {\mathbf {J}}_s(\tau )&=e\int {\mathbf {V}}{\mathcal {P}}({\mathbf {V}})d^3{V}\nonumber \\&=e\int ^{\tau }_{-\infty }\mathrm{d}\tau '\frac{\partial \rho _e}{\partial \tau '}{\mathbf {V}}(\tau ',\tau ) \end{aligned}$$
(10)

and the generated electric field

$$\begin{aligned}&{\mathbf {E}}_s(\tau )\sim \frac{1}{\varepsilon _0}\int ^{\tau }_{\infty }\mathrm{d}\tau '{\mathbf {J}}_s(\tau ')\nonumber \\&\quad =\frac{e}{\varepsilon _0}\int ^{\tau }_{\infty }\mathrm{d}\tau '\int ^{\tau '}_{-\infty }\mathrm{d}\tau ''\frac{\partial \rho _e}{\partial \tau ''}{\mathbf {V}}(\tau '',\tau '). \end{aligned}$$
(11)

From Fig. 4, we can see clearly that the electric components (\(E_{X,Y,Z}\)) along the three orthogonal directions are excited around \(\tau =4.0\) fs. Particulary, the component \(E_X\) (green dashed line) has the opposite sign with the initial laser pulse (blue solid line), which means the decay of the incident electric field polarized along \({\mathbf {x}}\)-axis. Part of the laser energy is transferred into its components in \({\mathbf {y}}\)- and \(\xi\)-directions by the ionized electrons.

Fig. 4
figure 4

Incident electric field (left-hand side ordinates) and generated field components (right-hand side ordinates) after 0.1 \(\upmu\)m propagation

Full size image

3.2 Energy partitions

During the energy transfers and conversions, certain amount of the laser energy is carried by the ionized electrons in the form of kinetic energy, which causes the generation of electric field along \({\mathbf {y}}\)- and \({\xi }\)-axes, the heating of the partially ionized gaseous medium, and thus the rapid loss of the total laser energy. To trace out the process of the energy transfer, we calculate the normalized energy (flux) carried by the laser pulse, \(P(\xi )=\int ^{+\infty }_{-\infty }|{\mathbf {E}}(\xi ,\tau )|^2 \mathrm{d}\tau /P_0\), where \(P_0={\int ^{+\infty }_{-\infty }|{\mathbf {E}}_\mathrm{in}|^2(\tau )\mathrm{d}\tau }\) represents the incident laser energy. Since the transverse refraction has been omitted during the laser’s propagation, the laser energy is represented as energy density without confusion. Here, we separate the laser energy into four parts: the energies carried by the electric field polarized along \({\mathbf {x}}\)-, \({\mathbf {y}}\)- and \({\xi }\)-axes, respectively, and the laser loss that deposited into the gaseous medium (including atomic ionization and others),

$$\begin{aligned} P_j(\xi )&=\frac{1}{P_0}{\int ^{+\infty }_{-\infty }E_j^2(\xi ,\tau )\mathrm{d}\tau }, \end{aligned}$$
(12)
$$\begin{aligned} P_\mathrm{loss}({\xi })&=1-\sum _{j=x,y,\xi } P_j(\xi ), \end{aligned}$$
(13)

where \(E_j(\xi ,\tau )\) is the jth component of the laser field at the distance of \(\xi\). The \(P_\mathrm{loss}\) is defined by the energy conservation law. The blue solid line represents the evolution of the energy density of the x-component of laser field, and the green solid line represents that of the y-component of the laser field. The energy density carried by the \(\xi\)-component is plotted by red solid line. Moreover, the laser energy loss is also given by cyan dashed line. The four kinds of energy densities are approaching some stable values, because the maximal electric strength decreases below the ionization threshold and few electrons are produced.

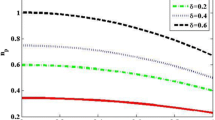
To explore the dependence of the energy partitions on the direction of the magnetic field, we calculate Eq. (12) for different orientation angles, \(\theta\) and \(\phi\). The angle \(\theta\) varies from 0 to \(\pi\) with a spacing \(\varDelta \theta =0.1 \pi\), and the angle \(\phi\) from 0 to \(2\pi\) with \(\varDelta \phi =0.2\pi\). The simulation results are presented in Fig. 5, from which we observe some interesting and precise symmetries,

$$\begin{aligned} P_x(\theta ,\phi )&=P_x(\theta ,\pi \pm \phi )=P_x(\theta ,2\pi -\phi )=P_x(\pi -\theta ,\phi )\nonumber ,\\ P_y(\theta ,\phi )&=P_y(\theta ,\pi +\phi )=P_y(\pi -\theta ,2\pi -\phi ),\nonumber \\ P_\xi (\theta ,\phi )&=P_\xi (\theta ,\pi +\phi )=P_\xi (\pi -\theta ,2\pi -\phi ). \end{aligned}$$
(14)
Fig. 5
figure 5

The dependence of energy transfers on the angles, \(\theta\) and \(\phi\). a \(P_x\); b \(P_y\); c \(P_{\xi }\). The parameters also are \(I_0=2\times 10^{15}\hbox { W/cm}^2\), and \(B = 2500\) T

Full size image

Based on the derivations above, the symmetries come from the mathematical structures of \(\varOmega\) in Eq. (6) or the matrix \({\mathbf {Q}}_j\) in Eq. (7). After careful examinations, we notice that the symmetries of the polarizations of the final laser pulse with respect to the angles are slightly different from that of the energy partitions,

$$\begin{aligned} E_x(\theta ,\phi )&=E_x(\theta ,\pi \pm \phi )=E_x(\theta ,2\pi -\phi )=E_x(\pi -\theta ,\phi )\nonumber ,\\ E_y(\theta ,\phi )&=E_y(\theta ,\pi +\phi )=-E_y(\pi -\theta ,2\pi -\phi ),\nonumber \\ E_\xi (\theta ,\phi )&=-E_\xi (\theta ,\pi +\phi )=-E_\xi (\pi -\theta ,2\pi -\phi ). \end{aligned}$$
(15)

In Eqs. (14) and (15), \(\theta\) and \(\phi\) are chosen as acute angles.

4 Conclusions

In summary, we investigate the intense laser pulse propagating through dilute gaseous medium in the presence of an external strong magnetic field which is characterized by its strength (B) and two angles (\(\theta\) and \(\phi\)). The treatments of responses from ionized electrons are performed by analytically solving the Lorentz equations.

The simulations show that the intense incident laser field causes significant ionizations of gaseous medium, which leads to the time-varying densities of medium constituents. The medium atoms first absorb sufficient energies from the incident laser field to release their electrons, and then the ionized electrons are accelerated by the laser electric field and the external magnetic field. The intense magnetic field bends the trajectories and velocities of the ionized electrons, and consequently the electric field components polarized along \({\mathbf {y}}\)- and \({\xi }\)-axes are generated according to Ampére’s law. By varying the angles \(\theta\) and \(\phi\), we find some interesting symmetries of the energy density partitions, which originate from the mathematical structure of evolutions matrix of electrons’ velocity (see Eq. (7)).

According to the analyses above, the polarization of the electric field can be modulated by varying the direction of the strong magnetic field. It indicates that the self-generated magnetic field by the laser-produced plasma will exert an influence on the incident laser pulse itself, and the consequent laser pulse will in turn change the dynamics of the plasma. The scheme proposed in this paper can be naturally generalized to picosecond or even longer laser pulses, where the collisions of the ionized electrons with other charged particles, the stimulated Raman scattering, the stimulated Brillouin scattering, etc., should all be taken into consideration. Moreover, the Cotton–Mouton effect will also play its role in influencing the incident laser pulse, especially for an ultrastrong magnetic field. From the macroscopic viewpoint, the Cotton–Mouton effect closely relates to the difference between the refractive coefficients of the propagation medium [21]. In our case, the medium components are time-dependent because of optical field ionization, and the ionized electrons are dominated. The Cotton–Mouton effect needs to be modeled by considering the microscopic processes, including the field ionization, dynamics of bound electron, and the acceleration the ionized electrons in the laser field and the external magnetic field.