1 Introduction

Airy wave packet was first introduced by Berry and Blazes as solutions of the potential-free Schrödinger equation within the context of quantum mechanism in 1979 [1]. The most remarkable feature of this Airy packet is its ability to freely accelerate even without any external potential. However, from a practical point of view, it is impossible to experimentally generate Airy packet due to its infinite energy. Until 2007, Christodoulides and Siviloglou predicted theoretically [2] and then observed experimentally [3] accelerating finite energy Airy beams in the area of optics. Such beam is characterized by a main intensity lobe that decays exponentially to zero on one side and decays with damped oscillations on the other. Several unique properties for these beams are diffraction-free, transverse acceleration, and self-healing [4], which lend it to some particular applications such as optical trapping and micro-manipulation [5,6,7], light bullets [8], curved plasma channel generation [9], optical routing [10], image signal transmission [11], vacuum electron acceleration [12], abrupt autofocusing [13], and so on.

In the past decade, many studies have been focused on the propagation and properties of Airy beams in linear and nonlinear media such as Kerr medium [14, 15], photorefractive (PR) media [16, 17], nonlocal nonlinear media [18], and have shown that the structure of Airy beams can be altered due to the existence of nonlinearity or amplitude and phase modulation [19,20,21]. On the one hand, linear Airy beam propagation allows soliton shedding when the initial Airy power is in a certain range, and the soliton exhibits periodical oscillation during propagation and moves along a straight trajectory [22,23,24,25,26,27]. Moreover, interactions of two shifted counter propagating Airy beams with a relative phase have also been researched in various nonlinear media, which can generate single solitons and soliton pairs [28,29,30]. On the other hand, there exists an additional class of accelerating beams in the presence of nonlinearity, namely nonlinear accelerating beams [31]. Propagation and interaction of such beams have been studied in different nonlinear media [32,33,34,35]. However, to the best of our knowledge, the related work has not been reported in biased PR media with quadratic electro-optic (EO) effect. Therefore, it is very important to investigate the dynamics and properties of Airy beams and nonlinear accelerating beams in such nonlinear media due to their potential applications of beam controlling and routing light in optical information processing field.

In this paper, we study the propagation dynamics of Airy beams and nonlinear accelerating beams in biased PR bulk media with quadratic EO effect by means of numerical simulations. In Sect. 2 we derive the basic equation of beam propagation and discuss the relation to the special case of a PR bulk media with quadratic EO effect under an external bias electric field. In Sect. 3 at first propagation of linear single Airy beam in the nonlinear media is investigated. It is found that, owing to the existence of stronger nonlinearity, localized beam state starts to form after shedding some radiation and propagates along a straight trajectory with periodic oscillations of amplitude and width; we call this beam breathing Airy soliton in this paper. Moreover, we discuss the propagation control of such soliton and its stability against small fluctuations. Later, interactions of two linear in-phase and out-of-phase Airy beams are studied. In particular we show that breathing solitons and soliton pairs are supported by varying the external bias electric field, the transverse separation, and the phase difference between the two Airy beams. In Sect. 4 we solve the nonlinear evolution equation numerically and also find that the interaction of nonlinear accelerating beams can produce breathing solitons and soliton pairs, and an interesting analogy to the interaction of nonlinear accelerating beams in dependence on the external bias electric field is shown. Section 5 contains our summary and conclusions.

2 Basic equation

In this section we consider an optical beam that propagates in an externally biased PR media with quadratic EO effect along the z axis and is permitted to diffract only along the x direction. For simplicity, only the one-dimensional nonlinear diffraction theory will be taken into account. The evolution of the beam is governed by the following nonlinear Schrödinger equation:

$$\left( {\frac{\partial }{{\partial z}} - \frac{i}{{2k}}\frac{{{\partial ^2}}}{{\partial {x^2}}}} \right)U\left( {x,z} \right)=\frac{{ik}}{{{n_{\text{e}}}}}\Delta nU\left( {x,z} \right),$$
(1)

where U(x, z) represents the slowly varying envelope of incident beam, \(\Delta n= - (1/2)n_{{\text{e}}}^{3}{g_{{\text{eff}}}}\varepsilon _{0}^{2}{({\varepsilon _{\text{r}}} - 1)^2}E_{{{\text{sc}}}}^{2}\) is the change in refractive index, ne is the unperturbed refractive index of the PR media, geff is the effective quadratic EO coefficient, ε0 and εr, respectively, are the vacuum and relative dielectric constants, Esc is the space-charge field inside the PR media, k = (2π/λ0)ne is the wave number, and λ0 is the free-space wavelength of the lightwave used. For relatively broad beam configurations, the space-charge field can be obtained from the Kukhtarev–Vinetskii model and is approximately given by [36]

$${E_{{\text{sc}}}}={E_0}\frac{{{I_\infty }+{I_{\text{d}}}}}{{I+{I_{\text{d}}}}},$$
(2)

where E0 denotes the externally applied electric field, I = |U(x, z)|2 is the intensity of the light beam, I∞ is a constant value of I at x → ± ∞, and Id is the dark irradiance of the media. Because of quadratic relation between the refractive index change and the space-charge field, the polarity of biasing field has no influence on the kind of nonlinearity. Only the sign of quadratic EO coefficient geff determines the nonlinearity (the sign is positive for self-focusing and negative for self-defocusing). In this paper, we are interested in the self-focusing nonlinearity (geff > 0) where the optical beam intensity is expected to vanish at infinity; thus, I∞ = 0. Moreover, for convenience, let us adopt the following dimensionless coordinates, i.e., let \(\xi =z/(kx_{0}^{2})\), \(s=x/{x_0}\), and \(q=I_{{\text{d}}}^{{ - 1}}U\), where x0 is an arbitrary transverse scale. By employing these latter transformations and by substituting Eq. (2) into Eq. (1),the dimensionless amplitude q(s, ξ) of the light field is found to satisfy [37]:

$$i\frac{{\partial q}}{{\partial \xi }}+\frac{1}{2}\frac{{{\partial ^2}q}}{{\partial {s^2}}} - \delta \frac{q}{{{{\left( {1+{{\left| q \right|}^2}} \right)}^2}}}=0.$$
(3)

Equation (3) has only one free parameter, δ, and the solution of Eq. (3) may be classified according to the value of this parameter and initial distribution of the field q(s, ξ) at ξ = 0. Here \(\delta ={k^2}x_{0}^{2}n_{{\text{e}}}^{2}{g_{{\text{eff}}}}\varepsilon _{0}^{2}{({\varepsilon _{\text{r}}} - 1)^2}E_{0}^{2}/2\) is proportional of the square of applied dc field E0. Obviously, we can adjust the external bias electric field to change the value of δ. For illustration purposes, let the photorefractive media be potassium lithium tantalate niobate (KLTN); we take the following parameters [38]: λ0 = 0.5 µm, ne = 2.2, x0 = 20 µm, geff = 0.12 m4 C− 4, εr = 8000.

3 Propagation of linear finite-energy Airy beams

When the third term in Eq. (3) is neglected, the equation reduces to a linear Schrödinger equation with an exact truncated solution for an Airy wave [2]

$$q(s,\xi )={A_0}\operatorname{Ai} \left( {s - \frac{{{\xi ^2}}}{4}+ia\xi } \right)\exp \left( {as - \frac{1}{2}a{\xi ^2} - \frac{1}{{12}}i{\xi ^3}+\frac{1}{2}i{a^2}\xi +\frac{1}{2}is\xi } \right),$$
(4)

where Ai(·) is the Airy function, A0 is the initial amplitude. The real decay factor a > 0 is a positive quantity that ensures the optical beam carries finite energy (we take a = 0.08 throughout). At the input plane, the initial field distribution for an Airy beam can be described by

$$q(s,\xi =0)={A_0}\operatorname{Ai} \left( s \right)\exp (as).$$
(5)

In the linear regime, A0 has no influence on the Airy solution of the linear Eq. (3) in free space. However, propagation of an optical beam in nonlinear media depends heavily on the initial power or amplitude because of the PR effect. Here, to investigate the dynamics of Airy beams, we change the parameters δ and A0, both of which can affect the strength of nonlinearity.

We first study the dynamics of one Airy beam propagation by varying δ with A0 = 1. Equation (3) is solved by means of the well-known split-step Fourier transform methods with Eq. (5) as an initial condition; the simulation results are shown in Fig. 1. For relative small external bias electric field (δ = 1), one can see in Fig. 1a that the Airy beam evolves by performing acceleration in free space and then exhibits diffraction properties. The inset in Fig. 1a presents the input truncated Airy amplitude profile at ξ = 0. When one sets δ = 3, and repeats the evolution, the corresponding result is displayed in Fig. 1b. As can be seen, a breathing Airy soliton can be formed out of the centered energy about the Airy main lobe as expected. The soliton exhibits periodic oscillations in the soliton intensity and width as a function of propagation distance. In addition, we note that the Airy wavefront continues to propagate along a parabolic trajectory (see the white dashed lines in Fig. 1). This is due to independence of linear waves and solitons in the pure nonlinear Schrödinger model (3). When δ = 5, it is shown in Fig. 1c that the soliton breathing period becomes shorter and the intensity stronger for the reason that the tail power of the Airy beam is almost trapped into the main lobe to shed a soliton due to the enhanced self-focusing effect. However, with further increasing δ until it is large enough, we found that the soliton width will become more and more narrow, i.e., the soliton breaks into filaments. Ultimately, the beam collapses as a result of catastrophic self-focusing effect. Also, similar results can be obtained by varying the initial amplitude A0 under an appropriate value of δ = 3.6038 which corresponds to E0 = 9000 V/m, as shown in Fig. 2. Curiously, for sufficient large A0, the soliton generated from the Airy main lobe will tilt to the right and additional weaker soliton states can emerge from the energy of the side lobe. The reason for such behavior is considered to be the conservation of momentum of Eq. (3), as found in [14].

Fig. 1
figure 1

Dynamics of linear truncated Airy beam for A0 = 1 and δ = 1 (a), 3 (b) and 5 (c), respectively. An inset in a is the input Airy beam profile. A thick white dashed line is a trajectory s = ξ2/4 of the Airy beam in a linear media

Full size image
Fig. 2
figure 2

Dynamics of linear truncated Airy beam for δ = 3.6038 and A0 = 1, 2 and 3, respectively

Full size image

We examined the dependences of the parameters of soliton, shedding from Airy main lobe, on A0 and δ. In Fig. 3a, b, the oscillations of soliton peak intensity are shown as a function of propagation distance for select values of A0 and δ, respectively. It is clear that all curves show a similar oscillating behavior, and the soliton mean peak intensity increases and the oscillation period (the period is defined as the distance between adjacent peaks or troughs of the oscillating soliton envelope) decreases with higher initial amplitude A0 or parameters δ. These oscillations about the soliton are known to arise as a result of the compensation between the diffraction and the nonlinear effect; they are not balanced but comparable.

Fig. 3
figure 3

Oscillations of soliton peak intensity for different A0 and δ. a δ = 3.6038; b A0 = 2.5

Full size image

All results described above were linked with solitons propagated along ξ-axis or tilted to the right at a small angle under higher initial amplitude. Next, we are interested in controlling the solitons’ propagation and discussing their stability in order to develop some potential applications of such soliton. To achieve such a purpose, we introduce a launch angle to the input Airy beam in the following form [39, 40]:

$$q(s,\xi =0)={A_0}\operatorname{Ai} (s)\exp (as)\exp (ivs),$$
(6)

where v is associated with the initial launch angle θ [θ = v/(kx0)] of the Airy beam; it can be controlled by varying the transverse displacement of the imaging lens with respect to the axis of the system in experiment.

Figure 4 shows the dynamics of an Airy beam for different values of v with A0 = 1 and δ = 3.6308. At the same time, we study the stability of the breathing Airy soliton by adding a Gaussian white noise (10% of the amplitude) to the initial beam. Immediately visible is that when v is negative, the shedding soliton tilts to the left (see Fig. 4a), when v = 0, it travels along ξ-axis (see Fig. 4b), and when v is positive, it deflects to the right (see Fig. 4c). The bigger the value of |v|, the greater the tilt angle of the soliton. In addition, the soliton propagates in a stable fashion over a long distance. Notice that, except for the output position, the change of launch angle has no influence on the intensity or width of the shedding soliton. As an example, one can see the soliton intensity plots in Fig. 4d–f corresponding to the white dashed lines (ξ = 20) in Fig. 4a–c, respectively.

Fig. 4
figure 4

a–c Deflection of soliton propagation for different v. d–f Soliton intensity plots corresponding to the location of white dashed lines (ξ = 20) in a–c, respectively

Full size image

After the investigation of dynamics of single Airy beam, we now turn to the numerical simulation of interaction between two linear Airy beams in PR media with EO effect. It is worth mentioning that a linear superposition of truncated Airy solutions also is a solution of Eq. (3) without nonlinearity. Therefore, we can assume that the incident beam is composed of two shifted counter propagating Airy beams with relative phase between them [28, 29, 35]:

$$\begin{aligned} q(s,\xi =0) & ={A_1}\operatorname{Ai} (s - B)\exp \left[ {a(s - B)} \right] \\ & \quad +{A_2}\operatorname{Ai} \left[ { - (s+B)} \right]\exp \left[ { - a(s+B)} \right]\exp (iQ), \\ \end{aligned}$$
(7)

where A1 and A2 are initial amplitudes of the two Airy beams, B is the transverse position shift between them, Q is the relative phase shift between the two components; in this paper, we restrict our simulations to two values of Q = 0 and Q = π, both of which correspond to in-phase and out-of-phase Airy beams, respectively.

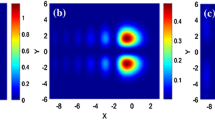
In Fig. 5 we display the evolution of the incident beam from Eq. (7) for various B and Q with A1 = A2 = 3 and δ = 3.6038. Because a large separation between Airy components in the incidence would lead to a weak interaction, here, we only show the cases of some relatively small separation. In the case in-phase (Q = 0), represented in Fig. 5a1–e1, both Airy components attract each other, and after collision, they fuse to a single bound breathing soliton, which periodically changes its amplitude and profile and propagates in a straight line in the center of the beam. Besides, additional weaker symmetric localized beams can also be formed out of the side lobes. With decreasing |B|, the attraction between the two components becomes stronger, and the intensities of side localized beams become more and more weak. For a phase difference Q = π, Fig. 5a2–e2 shows that both Airy components repel each other after collision, and bound breathing soliton pairs can generate from the two main and side lobes. As |B| decreases, the repulsion is gradually increased. Similar behavior has been reported in Kerr and saturable nonlinear media [28, 29].

Fig. 5
figure 5

Interactions of two linear Airy beams in PR media with quadratic EO effect for A1 = A2 = 3, δ = 3.6038, and selected values of B. a1–e1 In-phase case; a2–e2 out-of-phase case

Full size image

Since the external bias electric field has a remarkable influence on the propagation dynamics of single Airy beam, the interaction of two Airy beams is simulated by varying δ under given values of A1 = A2 = 3, and B = − 1, as displayed in Fig. 6a1–e2. Our calculations indicate that, as δ increased, the attraction between the two in-phase Airy beams increased and the soliton breathing period decreased (see Fig. 6a1–e1), but the repulsion between the two out-of-phase Airy beams decreased as well as the soliton pairs breathing period (see Fig. 6a2–e2). Note that, although the two out-of-phase components appear to be attracted as the external bias electric field increased in PR media with linear EO effect [35], we find that similar behavior does not show up for PR media with quadratic EO effect. In addition, when we set B = − 2 and redo the evolution of the interactions of the two in-phase Airy beams, the results are seen in Fig. 6a3–e3. It is very remarkable that two breathing solitons bifurcate from the interaction for both δ = 3 (see Fig. 6c3) and δ = 5 (see Fig. 6e3), respectively.

Fig. 6
figure 6

Interactions of two linear Airy beams in PR media with quadratic EO effect for A1 = A2 = 3 and selected values of δ. a1–e1 In-phase case with B = − 1; a2–e2 out-of-phase case with B = − 1; a3–e3 in-phase case with B = − 2

Full size image

4 Nonlinear accelerating beams

In addition to linear, we are also interested in seeking nonlinear accelerating beams: stationary solutions in accelerated frame. Because the only possible curve an accelerating beam can take is parabolic in the linear case, setting a travelling variable \(s - {\xi ^2}/4\) to substitute for s into Eq. (3) [31] yields

$$i\frac{{\partial q}}{{\partial \xi }} - i\frac{\xi }{2}\frac{{\partial q}}{{\partial s}}+\frac{1}{2}\frac{{{\partial ^2}q}}{{\partial {s^2}}} - \delta \frac{q}{{{{\left( {1+{{\left| q \right|}^2}} \right)}^2}}}=0.$$
(8)

In order to find the stationary accelerating solution of Eq. (8), the dimensionless amplitude q(s, ξ) can be written as \(q(s,\xi )=u(s)\exp \left[ {i\left( {s\xi /2+{\xi ^3}/24} \right)} \right]\), which gives rise to the following stationary equation:

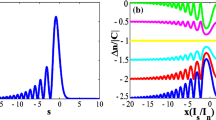
$$\frac{{{\partial ^2}u}}{{\partial {s^2}}} - su - \delta \frac{u}{{{{\left( {1+{{\left| u \right|}^2}} \right)}^2}}}=0.$$
(9)

Equation (9) can be solved by noting that the amplitude is small enough at s → ∞. Therefore, we can treat Eq. (9) as an initial value problem by using the boundary conditions \(u(s)=\alpha \operatorname{Ai} (s)\) and \(u^{\prime}(s)=\alpha \operatorname{Ai} ^{\prime}(s)\) at large s > 0 and integrate Eq. (9) from there on. Here α represents the nonlinearity strength induced by the potential solution. As an example, in Fig. 7a we display numerically obtained intensity profile of the accelerating mode at δ = 1 and α = 10. It is evident that this solution has the same Airy-like tail for s → − ∞ and possesses infinite energy. The beams tail is not identical to the Airy tail; it matches only asymptotically. As seen in Fig. 7b, the nonlinear solution accelerates along a parabolic trajectory. However, because of the infinite energy, it is reasonable to truncate the oscillation tail at an appropriate s and retain only ten lobes for obtaining finite energy beams. The corresponding propagation property is shown in Fig. 7c. One can see that the truncated solution sheds radiation but forms no solitons.

Fig. 7
figure 7

a Intensity of nonlinear accelerating beams at ξ = 0 with δ = 1 and α = 10. b Propagating accelerating solution and c truncated accelerating solution

Full size image

Similar to linear Airy beams’ interactions from Eq. (7), we now study the interactions of two truncated nonlinear accelerating beams which accelerate mutually in the opposite directions. The incident beam can be represented as

$$q(s,\xi =0)={q_1}(s - B)+\exp (iQ){q_2}\left[ { - (s+B)} \right],$$
(10)

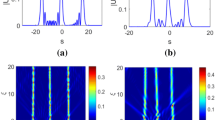
where q1 and q2 are two truncated accelerating solutions of Eq. (8). Due to the symmetry of the nonlinearity of the media, it is easy to obtain the solution of Eq. (9) in the opposite direction by directly reversing u(s) about s = 0. Figure 8 shows the propagation dynamics of two in-phase and out-of phase truncated nonlinear accelerating beams by varying the transverse separation and the relative phase difference with δ = 3.6038. Note that the position of the main lobe of the nonlinear solution moves to the left (s ≈ − 2.32), so we choose some relative small separations between the two beams to investigate their interactions. It is seen that the in-phase beams attract each other and shed an odd number of solitons after collision, while single breathing solitons with certain oscillating periods can only be formed in the center of the beam (see Fig. 8a1–e1). For the out-of-phase case, the two beams repel each other and generate soliton pairs, in which one soliton pair is originated from the main lobes, and the other from the side lobes. Curiously, the intensities of soliton pairs of the main lobes are stronger than that of side lobes in Fig. 8d2, but the behaviour is contrary in Fig. 8e2.

Fig. 8
figure 8

Interactions of truncated nonlinear accelerating beams in PR media with quadratic EO effect with δ = 3.6038, α = 10 and different transverse separations B. a1–e1 In-phase case; a2–e2 out-of-phase case

Full size image

We next change the value of parameter δ and repeat the simulations with B = − 2; the results are shown in Fig. 9. Interestingly, it is found that breathing solitons and soliton pairs can generate only within a certain range of the external bias electric field in the in-phase (see Fig. 9b1–d1) and out-of-phase cases (see Fig. 9b2–d2). Furthermore, in such simulation conditions we found that the upper and lower thresholds for the formation of single solitons and soliton pairs are δ = 5.39 and 1.31, respectively, meaning that the incident beams will subscribe to diffraction if the bias is too small or too big and no solitons exist, see examples in Fig. 9a1, e1, a2, and e2. For the range where breathing solitons or soliton pairs exist, with increasing δ, it is seen that the intensity amplitude increases and the attraction and repultion of the two truncated components become stronger in the in-phase and out-of-phase cases, respectively.

Fig. 9
figure 9

Interactions of truncated nonlinear accelerating beams in PR media with quadratic EO effect with B = − 2, α = 10 and different parameters δ. a1–e1 In-phase case; a2–e2 out-of-phase case

Full size image

5 Conclusion

In summary, we have investigated numerically the propagation behavior of linear Airy beams and nonlinear accelerating optical beams in biased PR media with quadratic EO effect. For linear Airy beams, single solitons can be formed by varying the initial amplitude and the external bias due to the existence of stronger nonlinearity. The breathing period of the soliton decreases and the soliton mean intensity increased with an increase of initial amplitude or external bias electric field. Furthermore, the solitons’ propagation direction can be controlled by introducing a launch angle and they can propagate stably. The interactions of both in-phase and out-of-phase linear Airy beams show that single solitons and soliton pairs can be produced during propagation, and their properties are affected heavily on the beams separation, relative phase difference, and the external bias electric field. For nonlinear accelerating beam, it has same Airy-like tail and possesses infinite energy. The interactions of two in-phase truncated nonlinear accelerating beams can generate an odd number of breathing solitons, and soliton pairs can be produced in the out-of-phase case. Interestingly, it is found that only solitons and soliton pairs can generate only within a certain range of the external bias electric field in the in-phase and out-of-phase cases: no soliton exists if the bias is too high or too low.