Direct electron acceleration for diagnostics of a laser pulse focused by an off-axis parabolic mirror

Abstract

We develop a theoretical basis for a new method of high-intensity ultrashort laser pulse diagnostics via vacuum electron acceleration from an ultrathin foil. A laser pulse is focused by an off-axis parabolic mirror, which has practical interest for most experiments with high-intensity pulses. The field description is based on Stratton–Chu integrals, which allow covering all focusing ranges up to the diffraction limit where the six-component laser field is correctly described. The theoretical approach uses a test particle method applicable for quite thin foils and rarefied gases, where the plasma fields do not substantially affect electron acceleration. The diagnostic method is to use measurements of angular-spectrum characteristics of laser accelerated or scattered electrons to compare them with the theory developed here. The proposed method can diagnose not only the intensity but also the quality of a laser pulse.

1 Introduction

After new techniques for amplifying a laser pulse such as CPA [1] and OPCPA [2] were developed, the light pulse energy of lasers with a fs/ps pulse duration has steadily increased. Many laser facilities have now attained petawatts of peak power [3,4,5,6,7] and will soon break through this level [8,9,10,11]. For such powerful lasers, the pulse intensity can be of unprecedented magnitude. Even now, sub-PW laser pulses can be focused into a spot size of a few wavelengths where the peak intensity can be as high as $\sim 10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$ [12, 13]. The quality of ultraintense laser pulses should undoubtedly be controlled with a high accuracy for efficiency in all kinds of laser-target experiments. There are worldwide techniques for laser intensity measurements. We mention one of them as detection of photoelectron yield [14], that allows to measure laser intensities with rather high accuracy but only for low intensities. Another approach is based on the estimation of a peak intensity, commonly derived from the temporal and spatial characteristics measured from an attenuated laser beam. However, for relativistically intense pulses this method is unlikely to give correct intensity evaluation due to wavefront tilting, recompression effects, mode distortions in the laser stretcher–amplifier–compressor chain [15]. Therefore, a development of new techniques is of high demand for laser pulse testing.

The most straightforward approach might be to irradiate charged particles with a laser, measure their angular-spectral distributions, and reconstruct the laser pulse characteristics from these measured distributions. Electrons, being most reactive to the laser field, have already been chosen as a carrier of information about the laser pulse [16, 17]. The corresponding nonlinear Thomson scattering can also be used [18, 19]. The proposed technique is based on the assumption that the interaction between particles (the collective field effect) is negligible compared with the interaction between the laser and particles. This condition can be satisfied by using ultrathin foils or rarefied gas in experiments. This method was recently tested experimentally in the interaction of a rarefied gas (at a pressure of $10^{-5}$ to $10^{-3}\,\hbox {mbar}$) with a Ti:sapphire laser pulse focused into a spot of diameter $2.2$ µm, and the results were compared with simulations of the electron interaction with a Gaussian-shaped laser pulse [20].

There are many works devoted to electron motion in the field of an electromagnetic pulse. If the laser spot size is sufficiently large compared with the laser wavelength, then the electromagnetic pulse can be described as a plane wave, and in accordance with the Lawson–Woodward theorem [21], a charged particle is accelerated by the leading edge of the pulse and decelerated by the trailing edge without a net energy gain [22, 23]. A sharper focusing results in an electron oscillation amplitude comparable to the focal spot size. Such a strongly inhomogeneous laser intensity makes the Lawson–Woodward theorem inapplicable and provides so-called vacuum electron acceleration. In this case, the commonly used paraxial approximation for laser beam propagation (see, e.g., [16]) is no longer applicable, and the very important regime of ultratight laser focusing requires an advanced approach for describing the laser field. For this, some works have used paraxial formulas with correction terms [24], and others have described the laser field by the exact solution of the vector Helmholtz equation deduced by the spectral method [18, 25] and with diffraction integrals [17, 26]. Popov took the first steps in studying electron dynamics in the field of a laser pulse focused by an on-axis parabolic mirror and noted some specific characteristics of electron acceleration by such a field configuration [26]. Nevertheless, this approach cannot claim to be suitable for practical experiments, which require a specific theory of charged particle acceleration from a tight focal spot. In turn, we have proposed a model of an off-axis mirror used in the most typical focusing scheme and have already tested this model for electron acceleration by homogeneous and Gaussian laser pulses [17].

In this paper, we present a detailed theoretical analysis of electron dynamics in a high-intensity laser pulse focused by an off-axis parabolic mirror up to the diffraction limit in the context of the important use of such a theory as a basis for advanced diagnostics of a tightly focused relativistically intense laser pulse. We use Stratton–Chu integrals, to which we devote Sect. 2. This approach allows quantitatively describing different spatial configurations of the incident laser beam. In Sect. 3, we describe the electron characteristics in detail depending on laser parameters such as peak intensity, focusing tightness, the spatial–temporal profile of the pulse, and its initial phase. Our study addresses the relations between the electron characteristics and the laser parameters as a new method for laser pulse diagnostics.

2 Laser fields of a pulse focused by an off-axis parabolic mirror

To describe a focused laser pulse, we use the model of a perfectly reflecting parabolic mirror [27] with a radius $\rho$ and an off-axis angle $\psi _{\mathrm{off}}$. We calculate the components of the laser field with Stratton–Chu integrals [28] and boundary conditions for incident (i) and reflection (r) beams at a point S (x, y, z) on the mirror surface A and at a point $Q(x_1,y_1,z_1)$ in the area of the reflected pulse propagation. In turn, the electric and magnetic fields ${\mathbf {E}}$ and ${\mathbf {B}}$ are defined by

$$ \begin{aligned} {\mathbf{E}}(S) & = {\mathbf{E}}_{i} + {\mathbf{E}}_{r} = 2{\mathbf{n}}({\mathbf{n}}\cdot{\mathbf{E}}_{i} ), \\ {\mathbf{H}}(S) & = {\mathbf{H}}_{i} + {\mathbf{H}}_{r} = 2{\mathbf{H}}_{i} - 2{\mathbf{n}}({\mathbf{n}}\cdot{\mathbf{H}}_{i} ), \\ {\mathbf{E}}(Q) & = \frac{1}{{4\pi }}\iint {\left( {2ik[{\mathbf{n}} \times {\mathbf{B}}_{i} ]G + 2({\mathbf{n}}\cdot{\mathbf{E}}_{i} )\nabla G} \right)}{\text{d}}A, \\ {\mathbf{B}}(Q) & = \frac{1}{{4\pi }}\iint {\left( {2[[{\mathbf{n}} \times {\mathbf{B}}_{i} ] \times \nabla G]} \right)}{\text{d}}A. \\ \end{aligned} $$

(1)

where ${\mathbf {n}}$ is a unit vector normal to the integration surface, ${\mathbf {k}}$ is the laser wave vector, $G=e^{ikr_{QS}}/ikr_{QS}$ is the Green’s function for the Helmholtz equation, and ${\mathbf {r}}_{QS}= \{\varDelta x_{QS},\,\varDelta y_{QS},\,\varDelta z_{QS}\}=\{(x-x_1),(y-y_1),(z-z_1)\}$. Because all calculations are done for a large focal length F of the parent mirror (Fig. 1) compared with the laser wavelength (i.e., $kF\gg 1$), we can neglect border effects [29].

If the optical axis of the parent mirror overlaps the z-axis, then we can describe the integration surface A as the part of the parabola given by $z=(x^2+y^2)/4F-F=F(s-1)$, and the unit vector ${\mathbf {n}}$ is equal to

$$\frac{1}{\sqrt{1+s}}\{-x/2F,-y/2F,1\}.$$

In the case of an off-axis mirror, its center is shifted on the x–z plane by a distance h in relation to the center of the parent mirror (Fig. 1). The integration area is then restricted by the inequality $(x-h)^2+y^2\le \rho ^2$.

An incident pulse directed along the optical axis is described by

$$\begin{aligned} {\mathbf{E}}_{i} & = (E_{{0x}} {\mathbf{e}}_{x} + E_{{0y}} {\mathbf{e}}_{y} )\exp ( - i(kz + \omega t + \phi _{0} )), \\ {\mathbf{B}}_{i} & = (E_{{0y}} {\mathbf{e}}_{x} - E_{{0x}} {\mathbf{e}}_{y} )\exp ( - i(kz + \omega t + \phi _{0} )), \\ \end{aligned}$$

(2)

where $\omega$ ($k=\omega /c$, and c is the speed of light) and $\phi _0$ are the frequency and the initial phase of the laser wave, and $E_{0x}(x,y)$ and $E_{0y}(x,y)$ are functions describing the laser spatial profile. If the phase of these functions is independent of the x and y coordinates, then the incident pulse has a plane front. After such a coordinate system is introduced, surface integrals (1) reduce to double integrals on the x–y plane.

Fig. 1

Scheme of a laser pulse focused by an off-axis parabolic mirror with the off-axis angle $\psi _\mathrm{off}$, the mirror radius $\rho$, and the respective focal lengths of the parent and off-axis mirrors F and $F_\mathrm{eff}$

For this geometry of the focusing system and light beam propagation, the electric field of the considered laser pulse (1) is represented as

$$ {\mathbf{E}} = \frac{1}{{2F\lambda }}\iint {\left(i{A}_{e} + \frac{{{a}_{e} }}{{kr_{{QS}} }}\right)}\cdot\frac{{{\mathbf{E}}_{i} e^{{ikl}} }}{{r_{{QS}}^{2} }}{\text{d}}x{\text{d}}y, $$

(3)

where $\lambda$ is the laser wavelength and the expressions for the magnetic field can be given by a suitable replacement ${\mathsf {A}}_e\rightarrow {\mathsf {A}}_b,$ and ${\mathsf {a}}_e\rightarrow {\mathsf {a}}_b$, where

$$ \begin{aligned} {\mathsf {A}}_e & = \left( {\begin{array}{*{20}l} {2Fr_{{SQ}} - x\Delta x_{{QS}} } \hfill & { - y\Delta x_{{QS}} } \hfill & 0 \hfill \\ { - x\Delta y_{{QS}} } \hfill & {2Fr_{{SQ}} - y\Delta y_{{QS}} } \hfill & 0 \hfill \\ {x\left( {r_{{SQ}} - \Delta z_{{QS}} } \right)} \hfill & {y\left( {r_{{SQ}} - \Delta z_{{QS}} } \right)} \hfill & 0 \hfill \\ \end{array} } \right), \\ {\mathsf {A}}_b & = \left( {\begin{array}{*{20}l} { - x\Delta y_{{QS}} } \hfill & {2F\Delta z_{{QS}} - y\Delta y_{{QS}} } \hfill & 0 \hfill \\ {x\Delta x_{{QS}} - 2F\Delta z_{{QS}} } \hfill & {y\Delta x_{{QS}} } \hfill & 0 \hfill \\ {2F\Delta y_{{QS}} } \hfill & { - 2F\Delta x_{{QS}} } \hfill & 0 \hfill \\ \end{array} } \right), \\ {\mathsf {a}}_e & = {\mathbf{r}}_{{SQ}} \cdot\left( {\begin{array}{*{20}c} x & y & 0 \\ \end{array} } \right),\quad {\mathsf {a}}_b = - {\mathsf {A}}_b , \\ l & = r_{{QS}} - F(s - 1) \\ & = \sqrt {r_{1}^{2} + r^{2} - 2(xx_{1} + yy_{1} + zz_{1} )} - F(s - 1), \\ \end{aligned} $$

(4)

and r and $r_1$ are the respective distances between the laser focus and points S (on the mirror surface) and Q (an observation point).

Because the integration surface of the off-axis mirror is asymmetric with respect to the center of the paraboloid, the reflected pulse propagates in the direction of the $z^{\prime}$-axis, which is found by rotating the z-axis about the y-axis through an angle $\psi _\mathrm{off}$. To analyze the characteristics of the focused pulse and the dynamics of an electron in the laser field, we use a primed coordinate system obtained by a rotation matrix:

$$\begin{aligned} x_{1} & = x^{\prime}\cos \psi _{{{\text{off}}}} - z^{\prime}\sin \psi _{{{\text{off}}}} , \\ z_{1} & = x^{\prime}\sin \psi _{{{\text{off}}}} + z^{\prime}\cos \psi _{{{\text{off}}}} , \\ y_{1} & = y^{\prime}, \\ \end{aligned}$$

(5)

where $\psi _\mathrm{off}$ is called the off-axis angle. The laser field components in the primed system can be derived from formulas (3) by an inverse transformation. In Fig. 1, the center ray of the reflected pulse corresponds to the line $A_1O$, which we use like an alignment axis for the off-axis angle. For the off-axis mirror, the effective focal length can be introduced as the length of $A_1O$ (Fig. 1), given by $F_\mathrm{eff}=2F/(1+\cos \psi _\mathrm{off})$.

One of the most important focusing characteristics is the f-number, $f_\#$, which describes a convergence angle of the light rays. If an incident pulse has a rectangular spatial profile with the diameter equal to the mirror size, then $f_\#$ is given by $f_\#=F_\mathrm{eff}/2\rho$. Increasing this parameter for the same intensity distribution corresponds to increasing of the laser focal spot size. The focal diameter as a function of $f_\#$ depends on the spatial form of the incident beam, which must be taken into account [17].

It is known that the components of the focused laser beam depend on the off-axis angle value [27]. Focal distributions of the laser field components are shown in Fig. 2. Here and hereafter, we omit the primes on the coordinates $(x^{\prime},y^{\prime},z^{\prime})$. The results are shown for homogeneous incident laser beams linearly polarized along the x-axis ($E_{x0}=$ const) and focused by mirrors with different off-axis angles. This is the only polarization that we consider in our paper. In the case of an on-axis mirror ($\psi _\mathrm{off}=0^{\circ }$), the $|E_x|^2$ and $|B_y|^2$ components have a maximum located in the laser pulse focus, which is shown in Fig. 2 for $f_\#=1.5$. The longitudinal components ($|E_z|^2$ and $|B_z|^2$) are dipolelike, while the $E_y$ and $B_x$ components have four maximums. The light components do not have the same amplitudes: for the results shown in Fig. 2, the ratios are $\left| {E_{z} } \right|_{{\max }}^{2} /\left| {E_{x} } \right|_{{\max }}^{2} = 1.4 \times 10^{{ - 2}}$ and $\left| {E_{y} } \right|_{{\max }}^{2} /\left| {E_{x} } \right|_{{\max }}^{2} = 3.7 \times 10^{{ - 5}}$.

Fig. 2

Distributions of the electric components for a laser beam with a homogeneous initial spatial profile in the focal plane of parabolic mirrors ($f_\#=1.5$) with $\psi _\mathrm{off}=0^{\circ }$ and $\psi _\mathrm{off}=60^{\circ }$, where $E_x$ is a component of the laser pulse polarization, $E_y$ is the other transverse component. and $E_z$ is the longitudinal component

As the off-axis angle increases, the $E_y$ and $B_x$ components are most sensitive to its changes. Their maxima unite in couples forming a dipolelike distribution on the focus plane (Fig. 2). At the same time, the comparative amplitude of their absolute values increases, and for $\psi _\mathrm{off}=60^{\circ }$ at $f_\#=1.5$, it attains $\left| {E_{y} } \right|_{{\max }}^{2} /\left| {E_{x} } \right|_{{\max }}^{2}=4.6\times 10^{-3}$. The structure of the light component distributions depends on the focus tightness and the off-axis angle, and at larger $f_\#$ values, the transition from a quadrupolelike to a dipolelike distribution occurs for a smaller off-axis angle.

This paper is devoted to estimating laser characteristics including the laser intensity, which is determined by the expression $I=c|{\mathbf {E}}|^2/8\pi$. Here, we are interested in its peak value $I_F$, which is attained in the center of the focal spot for all spatial laser distributions that we consider.

The features of the laser field components associated with the off-axis mirror geometry and the focal spot size must be taken into account to quantify the charged particle dynamics in strong laser fields. The next section is devoted to a detailed analysis of the particle motion and the theoretical background of a new method for the laser pulse diagnostics.

3 Dynamics of charged particles in the laser field

For the purposes of laser diagnostics, we should provide specific conditions under which the particle interaction forces are negligible compared with the laser strength and the particle dynamics is determined by the pulse parameters. This can be achieved in the case of a rarefied gas or ultrathin nanofoils. This approach allows using the test particle method to calculate the charged particle dynamics, which involves solving the relativistic equation of motion with the Lorentz force:

$$\frac{{{\text{d}}\gamma {\mathbf{v}}}}{{{\text{d}}t}} = \frac{q}{m}\left( {{\mathbf{E}} + \frac{{[{\mathbf{v}} \times {\mathbf{B}}]}}{c}} \right),\quad \frac{{{\text{d}}{\mathbf{R}}}}{{{\text{d}}t}} = {\mathbf{v}},$$

(6)

where q and m are the particle charge and mass, ${\mathbf {R}}$, ${\mathbf {v}}$, and $\gamma$ are the particle position vector, velocity, and Lorentz factor, and ${\mathbf {E}}$ and ${\mathbf {B}}$ are the real parts of the components in formulas (3). For ionized atoms, which are thousand of times heavier than an electron, this equation takes the nonrelativistic form under intensities lower than $10^{24}\,\hbox {W}\,\hbox {cm}^{-2}$ for $\lambda =0.8$ µm. At the same time, the electron behavior already becomes relativistic for intensities exceeding $10^{18}\,\hbox {W}\,\hbox {cm}^{-2}$. Here, we analyze the laser interaction with electrons in this intensity range.

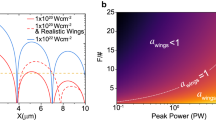
In addition to self-consistent plasma fields, we also neglect the effect of radiation friction force (RFF) in Eq. (6). This effect plays a significant role in the interactions of intensive laser pulses with oncoming beam of energetic electrons ($5 \times 10^{{22}} \,{\text{W}}\,{\text{cm}}^{{ - 2}}$ laser intensity and 40 MeV electrons [30]). Accounting for radiation damping effect reduces net energies of electrons and ions [31, 32]. In the recent work [33], it has been shown that for stronger and longer laser pulses ($10^{{23}} - 10^{{24}} \,{\text{W}}\,{\text{cm}}^{{ - 2}}$ and 125 fs) radiation friction results in enhanced production of longitudinal plasmas waves. In the case of ultrahigh power pulses, RFF also impacts dynamics of electrons initially at rest. The criterion for neglecting the RFF effect is formulated in the following way. The radiation friction force from classical approximation: $F_\mathrm{FF} \approx 2e^2\gamma ^2\omega ^2a_0^2/3c^2$ [22] [where $a_0=e E/(m\omega c)$ is the normalized laser amplitude] is compared with the Lorentz force, $F_{\text{L}} \approx a_0m\omega c$. This restricts $a_0$ in vacuum: $a_0 \ll 3 \lambda /4\pi r_e\gamma ^2$, where $r_e$ is the classical electron radius. For the plane-wave valuation of $\gamma$-factor [31, 34] this expression transforms to $a_0 \ll 50$. However, for a tight focusing considered here such an estimate is not correct. This is why we use both $a_0$ and $\gamma$ directly from numerical calculations to control the applicability of chosen model (Fig. 3). If this condition is violated, an overestimation of the electron energies occurs [35] and theoretical model should be advanced to apply to experiments.

Fig. 3

Applicability limit of the model neglecting RFF is shown with black line. Gray line corresponds to $a_0 \approx 215$ that refers to $I = 10^{23}\hbox { W}\hbox { cm}^{-2}$ for Ti:Sapphire lasers. Maximum energies attained in our calculations (see below Figs. 8, 12) are shown with triangle points

Fig. 4

Scheme of electron acceleration from an ultrathin foil by a focused laser pulse

We integrated trajectories independently by the Adams method [36] and the Boris scheme [37]. A good agreement between the results confirmed the calculation accuracy. To analyze the dependence of electron characteristics on the laser pulse parameters, we numerically computed the electron acceleration for particles regularly located in a monolayer imitating an ultrathin foil normal to the direction of the central ray propagation at a distance of the Rayleigh length ($z_{\text{R}}\equiv \pi D_{F}^2/4\lambda$, where $D_{F}$ is the focal spot diameter) in front of the beam focus. This configuration is shown schematically in Fig. 4. We chose the nanofoil size as $10D_{\text{FWHM}}\times 10D_{\text{FWHM}}$, where $D_{\text{FWHM}}$ is the focal spot diameter measured between points where the intensity is equal to half the maximum intensity. Unless otherwise specified, we used the following laser parameters: the incident laser pulse is linearly polarized with laser wavelength $\lambda =0.8$ µm and is focused by an off-axis parabolic mirror with $\psi _\mathrm{off}=60^{\circ }$. As in [18], we chose a temporal envelope given by the expression:

$$f(t,z)=\varTheta \left[ 1-\frac{|kz-\omega (t-\tau )|}{\omega \tau }\right] \cos ^2\left[ \frac{\pi }{2}\frac{(kz-\omega (t-\tau ))}{\omega \tau }\right] ,$$

where $\varTheta (x)$ is the Heaviside function and $\tau =70$ fs is a parameter characterizing the laser pulse duration, which corresponds to the half-maximum duration $\tau _{\text{FWHM}}\approx 26$ fs.

The model of laser–particle interaction that we consider here restricts the foil thickness in experiments by the inequality

$$\Delta z \ll \frac{{a_{0} n_{{{\text{cr}}}} }}{{\pi n_{e} }}\lambda , $$

(7)

where $n_\mathrm{cr}= m_e\omega ^2/(4\pi e^2)$ is the electron critical density equal to $1.7\times 10^{21}\,\hbox {cm}^{-3}$ for $\lambda =0.8$ µm, and $n_{e}$ is the electron density. This condition is based on comparing the laser field amplitude E with the Coulomb field, $E_\mathrm{pl}=2\pi en_e\varDelta z$. In accordance with Eq. (7), the lower the laser intensity is, the thinner the foil that should be used for the diagnostics. This estimate shows that a carbon foil with a thickness $<18\,\hbox {nm}$ should be used for the laser intensity $I=10^{21}\,\hbox {W}\,\hbox {cm}^{-2}$.

Here, we neglect spatial–temporal effects. The effect of the pulse duration on the spatial laser field distribution was analyzed in detail in [38], and this effect was also shown to be insignificant for $D_F<c\tau$.

3.1 Typical electron distributions

Fig. 5

a Angular distribution of electrons with net energy exceeding 50 KeV, and b net electron energy as a function of the initial position of the particle: the laser pulse characteristics are $D_{\text{FWHM}}\approx1.5\,\lambda$ and $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$

Fig. 6

Angular spectra of electrons accelerated by the laser pulse ($D_{\text{FWHM}}\approx1.5\,\lambda$, $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$) from an ultrathin nanofoil

In a recent work [17], we used the model presented in the preceding sections to compare angular spectra of particles accelerated by laser pulses with different radially symmetric spatial profiles, such as Gaussian and rectangular profiles, and laser pulses described by paraxial formulas. Here, we decided on a detailed analysis of the electron interaction with a homogeneous laser pulse for the purpose of laser diagnostics. Similarly to the previous work, we use a spherical coordinate system with angles $(\vartheta ,\,\varphi )$ with respect to the origin at the best focus position, where $\vartheta$ is the azimuthal angle (between a radius vector of the observed point and the z-axis) and $\varphi$ is the corresponding polar angle measured from the laser pulse polarization direction (from the x-axis in the x–y plane).

We obtained the results presented in this subsection for $f_\#=1.5$, $D_{\text{FWHM}}\approx1.5\lambda$, and the peak laser intensity $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$. We averaged the angular-spectral electron characteristics over the initial phase of the laser pulse in each subsection except the last, which is devoted to the phase effect.

The angular distribution of electrons with an energy exceeding 50 KeV is shown in Fig. 5a. It is almost isotropic in $\varphi$ with the maximum at $\vartheta _{\text{max}}\approx 45^{\circ }$. Similar results were found in [38] for lower intensities and larger focal spots. For $1-v_z/c\gg \lambda /(\pi D_F)$, the electron dynamics can be rather well described using the relativistic ponderomotive force, which predicts an isotropic electron distribution (with respect to the polar angle), unlike the case of a plane wave.

At the same time, the net electron energy depends on the electric components of the laser field, being proportional to the integral of the function $({\mathbf {v}}\cdot {\mathbf {E}})$ over time. Hence, the axial asymmetry of the $E_z$ component, shown in Fig. 2, introduces anisotropy into the distributions of the high-energy electrons. Figure 5b shows the final electron energy as a function of the initial electron position, which has maximums not on the z-axis matching the maximums of the longitudinal component of the electric field. But the ratio of the $E_z$ component to the polarization component is inversely proportional to the focal spot size $D_F$ [38, 39], which is why the demonstrated anisotropy disappears in the case of greater values of the beam focal diameter, when the $v_zE_z$ term in the integrand becomes negligible compared with $v_xE_x$. The dependence of the final energy on $({\mathbf {v}}\cdot {\mathbf {E}})$ also results in the area of electron acceleration having a ring shape, similarly to typical focal rings of a homogeneous laser beam [40].

The angular spectra of the accelerated particles are shown in Fig. 6. Because the particles located closer to the x–z plane gain greater energy (Fig. 5b), the electron spectrum as a function of $\varphi$ has peaks at $0^{\circ }$ and $180^{\circ }$ (Fig. 6a). High-energy electrons form jets propagating along the polarization plane, which were already shown in the case of an on-axis parabolic mirror [26].

The most energetic particles move closer to the direction of light propagation, which is shown in Fig. 6b. This result agrees with the plane electromagnetic wave approach [38], where the dependence of the Lorentz factor on $\vartheta$ is given by $\gamma =1+ 2/\mathrm{tan}^2\vartheta$. We previously showed [18] that outgoing electrons tend to be oriented along the pointing vector, which changes their escape angle in the case of a focused laser pulse compared with a plane laser wave.

3.2 Manipulation with laser power

Fig. 7

Characteristics of electrons accelerated by laser pulses with different peak intensities: a spectra, b cutoff energy, and c temperature of low-energy electrons

The maximum intensity can be controlled by both the laser peak power and the focal spot size. In this subsection, we calculate for homogeneous laser beams with different peak powers focused by an off-axis parabolic mirror with a fixed angular aperture $f_\#=1.5$ ($D_{\text{FWHM}}\approx1.5\,\lambda$). In Fig. 7a, we show the angle-integrated electron spectra for intensities from $10^{21}$ to $10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$. The results show that electrons gain more energy for a more powerful incident pulse. Such an energy increase is seen for both low-energy and high-energy electrons. It can be clearly seen that the electron cutoff energy $\epsilon _{\text{max}}$ increases with a peak intensity. For $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$, the electron energy $45\,\hbox {MeV}$ corresponds to a fourth order decrease of ${\text{d}}N/{\text{d}}\epsilon$, while for $I_F=5\times 10^{21}\,\hbox {W}\,\hbox {cm}^{-2}$, this value decreases to $30\,\hbox {MeV}$ (Fig. 7a, b). The most energetic electrons are accelerated in the process of their synchronization with the laser pulse, the so-called capture-and-acceleration (CAS) scenario [41], where an electron gains substantial net energy for a long time. Such particles form isolated high-energy peaks of the angular spectra and must be omitted in the laser diagnostics.

Reducing the laser power results in narrowing the area for electron acceleration to final energies exceeding 1 MeV. Calculations show that for $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$, the particles with energies exceeding 1 MeV are accelerated from the surface of $S_\mathrm{MeV}=66\,\lambda ^2$, while this area decreases to $S_\mathrm{MeV}=10\,\lambda ^2$ for $I_F=10^{21}\,\hbox {W}\,\hbox {cm}^{-2}$. With $S_\mathrm{MeV}$ and the known nanofoil parameters, the charge of MeV electrons can be estimated by the formula:

$$Q_\mathrm{MeV}=en_eS_\mathrm{MeV}\varDelta z.$$

(8)

In accordance with Eq. (8), a nanofoil with the same parameters as above, and $\varDelta z=5\,\hbox {nm}$, the considered charges, respectively, turn out to be 34 nC and 5 nC to satisfy condition (7).

One more characteristic that can be used to evaluate the intensity is the effective temperature $T_e$ of low-energy electrons, which characterizes its spectral slope. As is clear from Fig. 7a, the steepness of the slope of the electron spectra at low energies depends on the laser intensity and increases as the laser power decreases. To estimate $T_e$, we fit the particle distribution (${\text{d}}N/{\text{d}}\epsilon$) with the exponential $e^{-\epsilon /T_e}$ in the low-energy range ($\epsilon <2\,\hbox {MeV}$), where $\epsilon$ is the net electron energy. In Fig. 7c, we show this temperature as a function of the laser intensity.

3.3 Manipulation with focal spot size

Fig. 8

Characteristics of electrons accelerated by pulses with the same power $P \approx 200\,{\text{TW}}$ and different focal spot sizes: a spectra, b electron energy as a function of the peak intensity (including the case of a fixed focal spot size), the relation between the peak laser intensity and $f_\#$, and c distribution of electrons with energies exceeding 10 MeV

Table 1 The angular aperture $f_\#$, focal spot size $D_{\text{FWHM}}$, peak intensity $I_F$ for the laser power 195 TW, and total charge of MeV electrons accelerated from 18-nm foil

We performed several simulations for different values of the parameter $f_\#$ keeping the other laser pulse characteristics, i.e., $\hbox {P} \approx 200\,\hbox {TW}$, which corresponds to $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$ used in the preceding subsection for $f_\#=1.5$. We varied the focal spot diameter from $1.1$ to $6.2\,\lambda$ accompanied with an intensity decrease as shown in Table 1. A nanofoil was placed at a distance of the Rayleigh length in front of the focus, and its surface was expanded to values of $10D_{\text{FWHM}}\times 10D_{\text{FWHM}}$ (proportional to the focal spot size in each simulation). The calculations show that changing $f_\#$ from 1 to 4 results in increasing the cutoff energy $\epsilon _{\text{max}}$ (Fig. 8a) and the charge of the electrons with an energy exceeding 1 MeV (Table 1). We calculated the latter as in the preceding subsection. Increasing this parameter further accompanied by an intensity decrease and diameter expansion leads to reducing the maximum energy, which is similar to the results discussed in the preceding subsection (Fig. 8b). Hence, we observe a nonmonotonic response of the electron characteristics to variation of $f_\#$.

A similar behavior of electron energies as functions of the focal spot size was previously shown in works using simpified models of the focusing system less suitable for describing experiments in the cases of linearly polarized [18, 26] and radially polarized [42] laser pulses. This effect is explained as follows: in a high-intensity ultratightly focused laser pulse, the electron oscillation amplitude is comparable to the beam focal spot, and a particle, therefore, leaves the interaction area without attaining a high energy. Increasing the size of the focal spot results in a more efficient laser–particle interaction, even at a lower laser intensity. Correspondingly, if the focal spot size exceeds the electron oscillation amplitude, then decreased intensity due to focal expansion reduces the electron energy. As a result, inaccurately determining the focal spot size can lead to overestimating the laser peak intensity evaluated by the cutoff energy of angular-integrated spectra.

Possible ambiguities in interpreting diagnostic results by measuring the angular-integrated electron spectra require more sophisticated analysis-based angular measurements. The value of the laser beam convergence angle also affects the angular-spectral electron distributions, which can be used for additional diagnostics. In Fig. 8c, we show angular distributions of high-energy particles (with energy exceeding 10 MeV) for different $f_\#$ values. The escape angle of high-energy particles depends strongly on the focal spot size and increases as the focal diameter decreases, for example, being approximately $20^{\circ }$ for $f_\#=1.5$ and $27^{\circ }$ for $f_\#=1.0$. Hence, measuring the electron current in addition to angular-integrated spectra distributions can allow solving the problem of simultaneously evaluating the peak laser intensity and the focal spot size.

3.4 Effect of the spatial profile of the incident laser pulse

Fig. 9

a Focal pulse intensity profile for the Laguerre–Gaussian mode. b Energy spectra of accelerated electrons for homogeneous and Laguerre–Gaussian incident laser beam spatial profiles

As shown above, the spatial distributions of laser field components in the focal domain define the dynamics of the electrons accelerated from a nanofoil located near the focus. Varying the spatial profile of the incident pulse leads to a corresponding change in the electron distribution and consequently provides information about the laser pulse. We recently showed differences in the electron characteristics for Gaussian and homogeneous laser beam profiles with the same energies, powers, and focal spot sizes [17]. As a result, the intensive diffraction rings in Fig. 2 formed by focusing a homogeneous laser beam have a strong influence on the electron spectra.

As one more instructive example of practical interest, we consider an incident Laguerre–Gaussian laser beam, which can be described by

$$ E_{{0x}}^{{\lg }} = E_{0} e^{{ - \frac{{(x - h)^{2} + y^{2} }}{{\rho _{0}^{2} }}}} \cdot L_{1}^{0} \left( {2\frac{{(x - h)^{2} + y^{2} }}{{\rho _{0}^{2} }}} \right), $$

(9)

where $L^0_1(x)$ is the Laguerre polynomial given by $(1-x)$. The corresponding focal intensity distribution is given by a localized filament within an intensive ring (Fig. 9a). The intensity of the focal ring is comparable to the central peak intensity, which essentially affects the accelerated particle distributions. A similar laser configuration was recently used [43] to explain the results obtained in experiments on laser intensity estimation [20].

To compare the dynamics of electrons accelerated by laser beams with homogeneous or Laguerre–Gaussian spatial profiles, we chose corresponding laser pulses with the same energies, time durations, and diameters of the incident pulses. The latter was defined based on the area containing 99% of the laser power, whose peak value is 195 TW. Our calculations have been performed using $f_\#=1.5$ for the focusing mirror, which for the considered power of the Laguerre–Gaussian mode corresponds to $3.5\times 10^{21}\,\hbox {W}\,\hbox {cm}^{-2}$ of the peak intensity and $D_\mathrm{FWHM}=1.42\,\lambda$, in contrast to $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$ and $D_\mathrm{FWHM}=1.58\,\lambda$ for the focused homogeneous laser beam.

An initial spatial distribution with a high-intensity peripheral ring results in modifying the angle-integrated spectrum, demonstrating a peak of high-energy electrons (Fig. 9b). Similar results were presented for lower intensities ($I_F\approx 10^{20}\,\hbox {W}\,\hbox {cm}^{-2}$) of the laser pulse described via the lowest and first-order approximations of the solution of the Maxwell equations with a corresponding study of the electron spectra detected at different angles [43].

The cutoff energy in the spectrum of particles accelerated by the Laguerre–Gaussian mode is approximately equal to 35 MeV, which is less than in the case of acceleration by a homogeneous beam (Fig. 9b). The charge of particles accelerated to net energies exceeding 5 MeV increases from 5 nC for the homogeneous beam to 9.8 nC for the Laguerre–Gaussian beam. These electrons are initially located between the main central peak and the ring of the Laguerre–Gaussian mode, and can be divided into two representative groups. The particles in the first group are reflected by the peripheral ring and propagate at small angles almost collimated (within a cone of $<15^{\circ }$) because their propagation straightens on the edges of the central filament and the ring by their light pressures. The particles in the second group are pushed by the pondermotive force of the central intensity peak and cannot be reflected by the ring. The maximum of their angular distribution is attained at $\vartheta \approx 20^{\circ }$, which is equal to the escape angle of high-energy electrons accelerated by a focused homogeneous laser pulse. We, therefore, observe two angular peaks of high-energy electrons in the case of a focused Laguerre–Gaussian mode in contrast to acceleration in the case of a homogeneous pulse. Other particles, scattered by the light ring from the outside of the laser caustics, do not reach high energies and propagate at large angles with an angular maximum $\vartheta _\mathrm{max}\approx 60^{\circ }$, which is somewhat larger than in the case of a homogeneous laser pulse ($\vartheta _\mathrm{max}\approx 45^{\circ }$).

Our study shows how the laser beam spatial distribution can be diagnosed by analyzing the measured angular characteristics of accelerated electrons. At the same time, the particle dynamics is also determined by the temporal pulse profile, which we discuss in the next subsection.

3.5 Effect of the laser pulse temporal shape

Fig. 10

a Example temporal profile of a short laser pulse with a leading-edge shape defect (see Sect. 3.5). b Spectra of electrons accelerated by the laser pulse with and without (gray and black) this defect

An important problem is the diagnosis and control of the laser pulse temporal profile and its defects. Because the shape of the laser pulse can affect particle acceleration, this acceleration could be used for more advanced pulse diagnostics. There are several conventional methods for measuring the pulse power distribution in a wide temporal range [44, 45], but they are inapplicable to ultraintense pulses at the femtosecond/subpicosecond scale. Therefore, the main part of the pulse and the adjacent domains (pulse wings) can be depicted only roughly. Here, we pose the question whether direct electron acceleration can be used for such diagnostics.

The contributions, which affect the temporal intensity contrast ratio, can be roughly separated into three types: (1) prepulses on the nanosecond time scales before the main pulse relevant to ASE (amplified spontaneous emission), (2) prepulses on the picosecond time scales (mainly generated by nonlinear mixing of postpulses), and (3) deterioration of the rising slope of the main pulse (the example considered here). In our model, we neglect the ASE contribution to electron acceleration before the arrival of the main pulse. Since laser–matter interaction experiments require minimizing ASE, the technological work done during the last decade has led to a remarkable improvement in contrast (1), which for state-of-the-art lasers reaches $1:10^{12}$ [46]. Such high laser contrast prevents nanofoils from destructions and the finite contrast problem shifts toward the quality of the laser pulse at ps time scale (2), where the temporal intensity contrast ratio is significantly worse 1:($10^6- 10^{10}$) [6, 47, 48]. At the same time, not even a very high contrast, $\sim 1:10^6$, will produce only modest pre-acceleration electrons up to $\sim 100\hbox { eV}$ for laser intensity $10^{{21}} \,{\text{W}}\,{\text{cm}}^{{ - 2}}$ that is significantly less than characteristic electron energies, which can be used for diagnostic.

As an example, we chose a smooth laser power profile with a shape defect in the form of a femtosecond bell-shaped prepulse as shown in Fig. 10a. Similar distribution types were shown for modern petawatt facilities [6, 49]. Two Gaussian pulses shifted in time relative to each other are used to model this example. The prepulse has an amplitude 8.3 times less than the main pulse, which follows 46 fs behind it. We choose the total energy of both pulses with or without this defect to be the equal. We calculate for an off-axis mirror with $f_{\#}=1.5$, and the peak focal intensities of the defective and perfect pulses are also the same, $I_F=10^{22}\,\hbox {W}\,\hbox {cm}^{-2}$.

In Fig. 10b, we show the angle-integrated electron spectra for both pulse configurations. The calculations show that electrons are less energetic after acceleration by a laser beam with the shape defect corresponding to Fig. 10a. The lightweight particles are blown off by the prepulse without interaction with the main peak, which is why the resulting spectrum agrees with the spectrum of electrons accelerated by the low-intensity laser pulse considered above (Fig. 7a). Therefore, the approach with test electrons can be used only as a constituent part of more complicated diagnostics, for instance, involving acceleration of massive particles, such as protons, which interact with the entire laser pulse. We note that this point is worth considering in the future.

Fig. 11

The CEP of an ultrashort pulse

3.6 The carrier–envelope phase of ultrashort pulses

Fig. 12

Spectra of electrons accelerated by 3-fs laser pulses with different initial phases

One more laser pulse characteristic of interest for ultrashort pulses is the relative phase between the carrier and the envelope, the so-called carrier–envelope phase (CEP) $\varDelta \phi$ (cf. Fig. 11). Pulses of a few cycles of relativistic intensities can now be generated [50, 51], which opens a new field of research in high-energy field physics with lasers. Contemporary laser technologies allow controlling the CEP [52, 53], which is important, for example, for increasing the stability of few-cycle and single-cycle laser pulse interaction with plasma [54]. Results on wakefield acceleration with a 3.4-fs relativistic laser pulse without CEP stabilization were recently described [55]. Nevertheless, relevant simulations have shown the sensitivity to the CEP in agreement with theoretical works [56]. Direct electron acceleration has also been considered in the regime of few-cycle laser pulses, which is effective for producing high-energy electron bunches but is sensitive to the laser pulse phase [42]. The laser pulse phase could be used as a basis for CEP control.

We performed a series of simulations without initial phase averaging for a 3-fs laser pulse focused by two different off-axis mirrors with $f_\#=1.5$ and $f_\#=1$. We show the obtained electron spectra in Fig. 12, where “max” corresponds to a zero shift between the carrier and envelope phases, and “min” corresponds to $\varDelta \phi =\pi /2$. Our results show that the cutoff energy is sensitive to the CEP only in the case of ultratight focusing, for example, $f_\#=1.0$. Such diagnostics are, therefore, very restricted and should probably be supplemented by measurements of the radiation in the process of nonlinear Thomson/Compton scattering to achieve better certainty of the diagnostics.

Finally, we note that our calculations have also shown a dependence of the electron energy on the pulse duration. The angular-integrated electron spectra obtained for 3-fs laser pulses (Fig. 12) show a higher energy cutoff compared with the energies achieved in acceleration by a significantly longer 30-fs pulse (Fig. 8a). This shows a potential capacity of the direct electron acceleration method for measuring the pulse duration but requires more detailed study in the future. Moreover, such an ultrashort duration, considered in this subsection, is at the limit of the applicability condition for the temporal envelope approximation used in this paper and demands more accurate simulations, which should involve taking the effect of the temporal distribution on the spatial laser field distribution in the caustics into account.

3.7 Effect of possible uncontrollable parameters on intensity diagnostics

Besides the particular laser parameters, there are factors that can introduce certain variations in the experiments of the laser diagnostics. Some of them are concerned with stability and accuracy of the laser facility, the others can emerge because of low accuracy of the target positioning. We carried out a series of calculations with the same peak intensity of laser pulses, $I_F = 10^{22}\hbox { W}\hbox { cm}^{-2}$, to study impact of some possible uncontrollable parameters.

Fig. 13

Spectra of electrons accelerated by laser pulse with the peak intensity of $10^{22}\hbox { W}\hbox { cm}^{-2}$: “reference pulse”—laser pulse used in previous sections ($\tau \approx 26\, fs, D_\mathrm{FWHM} \approx 1.5\,\lambda$), “hot spot (X)”—initial spatial laser profile with a hot spot displaced from the beam center by half of its radius along x-axis, “hot spot (Y)”—initial spatial laser profile with a hot spot displaced from the beam center by half of its radius along y-axis, “extended pulse”—laser pulse duration being 5% longer than in the case of “reference pulse” and “focal plane”—target placed in the plane of best focus position

In addition to the contents of Sect. 3.5, where the laser pulse with fs-defect has been studied, we have considered the distortion of the laser pulse in terms of possible uncontrollable variations in its duration. The calculations have been performed for the laser pulse with the 5 % longer duration (Fig. 13, “extended pulse”) as compared to the 26-fs reference pulse (Fig. 13, “reference pulse”). The results show that the pulse extension over 5% leads to the 10% decreasing of the electron energy cutoff. At the same time, the temperature of low-energy particles remains unchanged. Thus, the minimization of the pulse duration fluctuations is an important aspect for more accurate diagnostics of the laser intensity.

Spatial laser beam distortions also could affect spectra of accelerated electrons. Among them we note hot spots, whose intensity can achieve or even exceed the maximum pulse intensity, and failure in positioning of the focusing mirror, that leads to the displacement of the laser beam relative to the mirror center. In our calculations, we simulated Gaussian hot spots with radius of $0.1\,\rho$ on the transversal spatial profile of the homogeneous incident laser pulse. The spots were displaced from the laser beam axis by a half of its radius along x direction [Fig. 13, “hot spot (X)”] and y direction [Fig. 13, “hot spot (Y)”]; on the mirror surface the amplitude of the laser field in the point of the hot peak was twice as large as in the points outside the hot spots. The focal spot of the hot spot perturbed pulse looks like the same one for the pulse without hot spots. The perturbed pulse can be represented by set of two pulses with different beam radius. Since the focal spot size varies in inverse proportion to the diameter of the incident pulse for the given focal length, the focused hot spot acts as a low-intensive background for the main spot in the focal plane. However, this changing of the spatial profile modifies spectral distributions of electrons (as seen in Fig. 13) and can be potentially identified.

Impact of the incident beam diameter fluctuations and beam positioning relative to the mirror center on the electron distributions can be evaluated via the results discussed in Sect. 7, because these distortions can be reduced to the variation of the focal spot size. Since focal diameter is proportional to $f_\#$, which is given by $F_\mathrm{eff}/(2\rho )$, relative errors in these diameters (the incident pulse and the focal spot) equal to each other. It means that 5%-changing of the beam diameter leads to the similar change in the focal spot size. Then, in accordance with Fig. 8b, the relative error of the cutoff energy and peak intensity evaluated through this figure, is estimated to be $1.5 \%$ and $3.6 \%$, respectively, for the given laser power and $f_\# = 1.5\, (D_{\text{FWHM}} \approx 1.5\,\lambda )$. Effect of mirror-beam misalignment, when their centers are shifted relative to each other, can be estimated through additional mirror with another off-axis angle. As it was shown above, $F_\mathrm{eff} = 2F/(1 + \cos \psi _\mathrm{off})$, for 5% error in the off-axis angle equal to $60^{\circ }$ the relative derivation of the effective focal length achieves 3%. In this case, the relative error of the focal spot is also 3%, that leads to 0.9% error in the cutoff electron energy and gives 2.2% error in the evaluated peak intensity for the discussed parameters.

As a final note, let us discuss a role of an accuracy in a target positioning. Figure 13 displays spectrum of electrons initially located in the plane of best focus position (“focal plane”), i.e., the electron spectrum for the ideally accurate foil positioning. We have carried out a series of calculations for the different positions of the nanofoil. The results have shown insignificant influence of the target position within the limits of Rayleigh length on the electron spectra.

To sum up, the method of diagnostics is sensitive to the uncertainties in the laser pulse duration and distortions of its spatial profile. This should be taken into account for the intensity estimation or could be used for quality rating of the laser beam. At the same time, this diagnostic approach is quite stable relative to small deviations in mirror and target positioning.

4 Conclusions

We have described the characteristics of electrons directly accelerated by a short tightly focused laser pulse from an ultrathin nanofoil for diagnosing different laser pulse parameters. We analyzed the results obtained theoretically for electron interactions with laser pulses of different peak powers, focal spot sizes, spatial–temporal profiles, and also CEP (in the case of ultrashort pulses) to find the relations between the spectral-angular characteristics of accelerated electrons and certain laser pulse parameters. Our advance in developing new, easy-to-handle, low-cost diagnostics is due to an accurate description of the laser fields of the pulse (using Stratton–Chu integrals [28]) focused by an off-axis parabolic mirror.

Studying the dependence of the electron dynamics on the laser intensity was central in our work. The intensity can be changed by varying either the laser power or the focal spot size. Our findings showed a different response of the electron characteristics depending on the way the intensity is changed. If the pulse intensity is changed by manipulating laser power, then there is monotonic change of the corresponding electron energy cutoff and the temperature of the low-energy electrons. Higher laser power results in a higher electron energy. But this is not the case if the laser intensity is changed by varying the tightness of the laser focusing. For such pulse manipulation, there is nonmonotonic dependence of the electron energy cutoff on the focal spot size (on the laser intensity). Although this fact is in accordance with previous works [18, 26, 42], our focusing model is of practical interest because it quantifies this effect with an off-axis mirror. The size of the focal spot (angular aperture) affects the angle of the energetic electron escape, which can be used in addition to the electron spectra to simultaneously measure both the peak intensity and the focal spot size. The simulations also showed a sensitivity of the electron dynamics to the spatial–temporal laser profile, which is also useful for laser diagnostics. But with regard to evaluation of the CEP, the relative advantage of the new method can be thought of as related to ultratight focusing and very accurate measurements, which are still problematic.

The method of diagnostics proposed is sensitive to the uncertainties in the laser pulse duration and distortions of laser beam spatial profile. This should be taken into account for the intensity estimation or could be used for quality rating of the laser beam. At the same time, this diagnostic approach is quite stable relative to small deviations in mirror and foil positioning.

Further development of the diagnostic method proposed for an off-axis parabolic mirror should be aimed at analyzing electron acceleration in the laser interaction with a rarefied gas. The effect of nonlinear Thomson scattering and proton acceleration as diagnostic tools could also be considered using the approach developed here. One more important future step should be to consider laser pulses with other polarizations, such as circular, radial, and azimuthal: their diagnostics are in high demand because of several advantages of exotic polarizations for laser-triggered particle acceleration.