1 Introduction

It is well known that an optical vortex and an edge dislocation are two kinds of phase dislocations [1, 2]. The optical vortex is connected to the orbital angular momentum of light, whose helical phase fronts are described by \(\exp \left( {in\theta } \right)\), where θ is the azimuthal angle, and \(n\hbar\) is the orbital angular momentum carried per photon [3]. The edge dislocation with π-shift is located along a curve at transverse plane [4]. Much interest has been exhibited in optical beams carrying phase singularity because of their potential applications in optical manipulation, optical data storage, optical communications and biological tissues [5,6,7,8,9,10,11,12,13,14,15]. Vortex beam generation methods have been proposed [16,17,18]. Chen et al. proposed a simple method for simultaneous determination of the sign and the magnitude of the topological charge of a partially coherent vortex beam [19]. Cheng et al. reported energy flux density and angular momentum density of Pearcey–Gauss vortex beams in the far field [20]. Chen et al. studied the propagation characteristics of ring Airy Gaussian vortex beams [21]. Qu et al. investigated that plasma q-plate for generation and manipulation of intense optical vortices [22]. Zhang and Wang have studied the propagation dynamics of off-axis symmetrical and asymmetrical vortices embedded in flat-topped beams [23]. The transformation of optical vortices propagating through atmospheric turbulence was reported in [24, 25]. The dynamic trajectory of the noncanonical vortex has significant deviations from their canonical counterparts of the same topological charge [26, 27].

In this paper, we studied the transformation of an optical vortex and an edge dislocation propagating through atmospheric turbulence. In the second section, the analytical expressions for the cross-spectral density function of mixed screw-edge dislocations beams propagating through atmospheric turbulence are derived. The evolution behavior of mixed screw-edge dislocations propagating through atmosphere turbulence is studied in the third section. The fourth section summarizes the main results of this paper.

2 Theoretical model

The initial field distribution of mixed screw-edge dislocations beams at the source z = 0 can be expressed as follows [28, 29]:

$$E\left( {{\varvec{s}}{\text{, }}z=0} \right)=\frac{{\left( {a{s_x}+\text{i}{s_y}} \right)\left( {{s_x} - b} \right)}}{{{w^2}}}\exp \left( { - \frac{{s_{x}^{2}+s_{y}^{2}}}{{{w^2}}}} \right),$$
(1)

where s = (sx, sy) is a 2D position vector, w is the waist width of mixed screw-edge dislocations beams, b denotes the off-axis distance of edge dislocation, and a is a dimensionless parameter, if a < 0, an optical vortex phase of mixed dislocations rotates clockwise, if a > 0, the optical vortex phase rotates anticlockwise. Figure 1 presents the phase distribution and normalized intensity distribution of mixed screw-edge dislocations beams at the source plane. The calculation parameters are w = 3 cm, a = 2, and b = 1 cm. From Fig. 1 we see that in mixed screw-edge dislocations beams there exist an edge dislocation and a noncanonical optical vortex with topological charge + 1 because phase increment around the optical vortex is unlinear with the azimuthal angle [27].

Fig. 1
figure 1

a Phase distribution and b normalized intensity distribution of mixed screw-edge dislocations beams at the source plane

Full size image

The cross-spectral density function of mixed screw-edge dislocations beams at the source plane z = 0 is expressed as

$$\begin{aligned} {W_0}\left( {{{\varvec{s}}_1},{{\varvec{s}}_2},z=0} \right) & =\left\langle {{E^{\text{*}}}({{\varvec{s}}_1},0)E({{\varvec{s}}_2},0)} \right\rangle \\ & {\kern 1pt} =\frac{1}{{{w^4}}}\sum\limits_{{l=0}}^{1} {\frac{{{{\left( {a{s_{1x}}} \right)}^l}{{\left( { - iy} \right)}^{1 - l}}}}{{l!\left( {1 - l} \right)!}}} \left( {{s_{1x}} - b} \right)\exp \left( { - \frac{{s_{{1x}}^{2}+s_{{1y}}^{2}}}{{{w^2}}}} \right) \\ & \quad \times \sum\limits_{{m=0}}^{1} {\frac{{{{\left( {a{s_2}_{x}} \right)}^m}{{\left( {iy} \right)}^{1 - m}}}}{{m!\left( {1 - m} \right)!}}} \left( {{s_{2x}} - b} \right)\exp \left( { - \frac{{s_{{2x}}^{2}+s_{{2y}}^{2}}}{{{w^2}}}} \right), \\ \end{aligned}$$
(2)

where * denotes the complex conjugate.

In accordance with extended Huygens–Fresnel principle [30], the cross-spectral density function of mixed screw-edge dislocations beams propagating through atmospheric turbulence can be calculated as

$$\begin{aligned} W\left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right) & ={\left( {\frac{k}{{2\uppi z}}} \right)^2}\int {\int {\int {\int {{W_0}} } } } \left( {{{\varvec{s}}_1},{{\varvec{s}}_2},z=0} \right)\exp \left\{ { - \frac{{\text{i}k}}{{2z}}\left[ {{{\left( {{{\varvec{s}}_1} - {\varvec{\rho}_1}} \right)}^2} - {{\left( {{{\varvec{s}}_2} - {\varvec{\rho}_2}} \right)}^2}} \right]} \right\} \\ & \quad {\kern 1pt} \times \left\langle {\exp \left[ {{\psi ^*}\left( {{\varvec{\rho}_1}, {{\varvec{s}}_1}} \right)+\psi \left( {{\varvec{\rho}_2}, {{\varvec{s}}_2}} \right)} \right]} \right\rangle {\text{d}}{{\varvec{s}}_1}{\text{d}}{{\varvec{s}}_2}, \\ \end{aligned}$$
(3)

where ρ1 = (ρ1x, ρ1y) and ρ2 = (ρ2x, ρ2y) denote the position vector at the z plane, k = 2π/λ is the wave number, <\(\cdot\)> denotes the average over the ensemble of the atmosphere turbulence. \(\left\langle {\exp \left[ {{\psi ^*}\left( {{\varvec{\rho}_1}, {{\varvec{s}}_1}} \right)+\psi \left( {{\varvec{\rho}_2}, {{\varvec{s}}_2}} \right)} \right]} \right\rangle\) can be written as [31]

$$\left\langle {\exp \left[ {{\psi ^*}\left( {{\varvec{\rho}_1},{{\varvec{s}}_1}} \right)+\psi \left( {{\varvec{\rho}_2},{{\varvec{s}}_2}} \right)} \right]} \right\rangle \approx {\text{exp}}\left[ { - \frac{{{{\left( {{{\varvec{s}}_1} - {{\varvec{s}}_2}} \right)}^2}+{{\left( {{\varvec{\rho}_1} - {\varvec{\rho}_2}} \right)}^2}+\left( {{{\varvec{s}}_1} - {{\varvec{s}}_2}} \right)\left( {{\varvec{\rho}_1} - {\varvec{\rho}_2}} \right)}}{{\rho _{0}^{2}}}} \right],$$
(4)

where \({\rho _0}={(0.545C_{n}^{2}{k^2}z)^{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}\) denotes the spatial coherence radius of a spherical wave propagation through atmospheric turbulence and \(C_{n}^{2}\) specifies the refraction index structure constant. The larger the \(C_{n}^{2}\), the stronger the atmospheric turbulence.

Substituting Eqs. (2) and (4) into Eq. (3), we adopt the following integral formula [32]:

$$\int {{x^n}\exp \left( { - p{x^2}+2qx} \right)} {\text{d}}x=n!\exp \left( {\frac{{{q^2}}}{p}} \right)\sqrt {\frac{\pi }{p}} {\left( {\frac{q}{p}} \right)^n}\sum\limits_{{k=0}}^{{E\left[ {\frac{n}{2}} \right]}} {\frac{1}{{\left( {n - 2k} \right)!k!}}{{\left( {\frac{p}{{4{q^2}}}} \right)}^k}} ,\quad \left( {n=0,{\text{ }}1,{\text{ }}2 \ldots } \right).$$
(5)

We obtain analytical expressions for the cross-spectral density function of mixed screw-edge dislocations beams propagating through atmospheric turbulence, which is given by

$$\begin{aligned} W\left( {{\rho _1},{\rho _2},z} \right) & =\frac{1}{{{w^4}}}{\left( {\frac{k}{{2\pi z}}} \right)^2}\exp \left[ { - \frac{{{{\left( {{\rho _1} - {\rho _2}} \right)}^2}}}{{\rho _{0}^{2}}}} \right]\exp \left[ { - \frac{{ik}}{{2z}}\left( {\rho _{1}^{2} - \rho _{2}^{2}} \right)} \right] \\ & \quad {\kern 1pt} \times \sum\limits_{{l=0}}^{1} {\sum\limits_{{m=0}}^{1} {\sum\limits_{{k=0}}^{{E\left[ {\frac{{1 - m}}{2}} \right]}} {\sum\limits_{{h=0}}^{{1 - m - 2k}} {\sum\limits_{{q=0}}^{{E\left[ {\frac{{1 - l+h}}{2}} \right]}} {\frac{{\pi {a^{l+m}}{{\left( { - i} \right)}^{1 - l}}{{\left( i \right)}^{1 - m}}\left( {1 - m} \right)!{A^{m - 1}}{A^k}}}{{{4^k}\sqrt {AC} l!\left( {1 - l} \right)!m!\left( {1 - m} \right)!\left( {1 - m - 2k} \right)!k!}}} } } } } \\ & \quad \times \frac{{\left( {1 - m - 2k} \right)!\left( {1 - l+h} \right)!}}{{h!\left( {1 - m - 2k - h} \right)!\left( {1 - l+h - 2q} \right)!q!}}{\left( {\frac{{{B_y}}}{2}} \right)^{1 - m - 2k - h}}{\left( {\frac{1}{{\rho _{0}^{2}}}} \right)^h}{\left( {\frac{D}{C}} \right)^{1 - l+h}} \\ & \quad \times \left( {\frac{C}{{4{D^2}}}} \right)\exp \left( {\frac{{B_{y}^{2}}}{{4A}}+\frac{{{D^2}}}{C}} \right)\left\{ {\left[ {E\left( {F - bG} \right) - Hb\left( {L - bM} \right)} \right]} \right\}, \\ \end{aligned}$$
(6)

where

$$A=\frac{1}{{{w^2}}} - \frac{{\text{i}k}}{{2z}}+\frac{1}{{\rho _{0}^{2}}},$$
(7)
$${B_y}= - \frac{{\text{i}k{\rho _{2y}}}}{z}+\frac{{{\rho _{1y}} - {\rho _{2y}}}}{{\rho _{0}^{2}}},$$
(8)
$$C=\frac{{\text{i}k}}{{2z}}{\text{+}}\frac{1}{{\rho _{0}^{2}}}{\text{+}}\frac{1}{{{w^2}}} - \frac{1}{{A\rho _{0}^{4}}},$$
(9)
$$D=\frac{{\text{i}k{\rho _{1y}}}}{{2z}} - \frac{{{\rho _{1y}} - {\rho _{2y}}}}{{2\rho _{0}^{2}}}+\frac{{{B_y}}}{{2A\rho _{0}^{2}}},$$
(10)
$$E=\sum\limits_{{j=0}}^{{E\left[ {\frac{{1+m}}{2}} \right]}} {\sqrt {\frac{\pi }{A}} \frac{{\left( {m+1} \right)!{A^{ - \left( {m+1} \right)}}{A^j}}}{{{4^j}\left( {m+1 - 2j} \right)!j!}}} \sum\limits_{{p=0}}^{{E\left[ {\frac{{1+m - 2j}}{2}} \right]}} {\frac{{\left( {m+1 - 2j} \right)!}}{{\rho _{0}^{{2p}}\left( {m+1 - 2j - p} \right)!p!}}{{\left( {\frac{{{B_x}}}{2}} \right)}^{m+1 - 2j - p}}} \exp \left( {\frac{{B_{x}^{2}}}{{4A}}} \right),$$
(11)
$$F=P\left( {l+p+1} \right)!{\left( {\frac{{2AO\rho _{0}^{4} - {B_x}\rho _{0}^{2}}}{{2\left( {AN\rho _{0}^{4} - 1} \right)}}} \right)^{l+p+1}}\sum\limits_{{{h_{\text{1}}}=0}}^{{E\left[ {\frac{{l+p+1}}{2}} \right]}} {\frac{1}{{\left( {l+p+1 - 2{h_{\text{1}}}} \right)!{h_{\text{1}}}!}}} {\left( {\frac{{A\left( {AN\rho _{0}^{4} - 1} \right)}}{{{{\left( {2AO\rho _{0}^{2} - {B_x}} \right)}^2}}}} \right)^{{h_{\text{1}}}}},$$
(12)
$$G=P\left( {l+p} \right)!{\left( {\frac{{2AO\rho _{0}^{4} - {B_x}\rho _{0}^{2}}}{{2\left( {AN\rho _{0}^{4} - 1} \right)}}} \right)^{l+p}}\sum\limits_{{{h_{\text{2}}}=0}}^{{E\left[ {\frac{{l+p}}{2}} \right]}} {\frac{1}{{\left( {l+p - 2{h_{\text{2}}}} \right)!{h_{\text{2}}}!}}} {\left( {\frac{{A\left( {AN\rho _{0}^{4} - 1} \right)}}{{{{\left( {2AO\rho _{0}^{2} - {B_x}} \right)}^2}}}} \right)^{{h_{\text{2}}}}},$$
(13)
$$H=\sum\limits_{{u=0}}^{{E\left[ {\frac{m}{2}} \right]}} {\sqrt {\frac{\pi }{A}} \frac{{\left( m \right)!{A^u}{A^{ - m}}}}{{{4^u}\left( {m - 2u} \right)!u!}}} \sum\limits_{{v=0}}^{{E\left[ {\frac{{m - 2v}}{2}} \right]}} {\frac{{\left( {m - 2u} \right)!}}{{\rho _{0}^{{2v}}\left( {m - 2u - v} \right)!v!}}{{\left( {\frac{{{B_x}}}{2}} \right)}^{m - 2u - v}}} \exp \left( {\frac{{B_{x}^{2}}}{{4A}}} \right),$$
(14)
$$I=P\left( {l+v+1} \right)!{\left( {\frac{{2AO\rho _{0}^{4} - {B_x}\rho _{0}^{2}}}{{2\left( {A\rho _{0}^{4}N - 1} \right)}}} \right)^{l+v+1}}\sum\limits_{{{h_{\text{3}}}=0}}^{{E\left[ {\frac{{l+v+1}}{2}} \right]}} {\frac{1}{{\left( {l+v+1 - 2{h_{\text{3}}}} \right)!{h_{\text{3}}}!}}} {\left( {\frac{{A\left( {A\rho _{0}^{4}N - 1} \right)}}{{{{\left( {2AO\rho _{0}^{2} - {B_x}} \right)}^2}}}} \right)^{{h_{\text{3}}}}},$$
(15)
$$M=P\left( {l+v} \right)!{\left( {\frac{{2AO\rho _{0}^{4} - {B_x}\rho _{0}^{2}}}{{2\left( {A\rho _{0}^{4}N - 1} \right)}}} \right)^{l+v}}\sum\limits_{{{h_{\text{4}}}=0}}^{{E\left[ {\frac{{l+v}}{2}} \right]}} {\frac{1}{{\left( {l+v - 2{h_{\text{4}}}} \right)!{h_{\text{4}}}!}}} {\left( {\frac{{A\left( {A\rho _{0}^{4}N - 1} \right)}}{{{{\left( {2AO\rho _{0}^{2} - {B_x}} \right)}^2}}}} \right)^{{h_{\text{4}}}}},$$
(16)
$$N=\frac{{\text{i}k}}{{2z}}{\text{+}}\frac{1}{{\rho _{0}^{2}}}{\text{+}}\frac{1}{{{w^2}}},$$
(17)
$$O=\frac{{ik{\rho _{1x}}}}{{2z}}+\frac{{{\rho _{1x}} - {\rho _{2x}}}}{{2\rho _{0}^{2}}}$$
(18)
$$P=\exp \left( {\frac{{{{\left( {2AO\rho _{0}^{2} - {B_x}} \right)}^2}}}{{4A\left( {AN\rho _{0}^{4} - 1} \right)}}} \right)\sqrt {\frac{{A\rho _{0}^{4}\pi }}{{A\rho _{0}^{4}N - 1}}} .$$
(19)

According to the symmetry, Bx can be obtained by replacing ρ1y, and ρ2y in By with ρ1x, and ρ2x.

The spectral degree of coherence is defined as [33]

$$\mu \left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right)=\frac{{W\left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right)}}{{{{\left[ {I\left( {{\varvec{\rho}_1},z} \right)I\left( {{\varvec{\rho}_2},z} \right)} \right]}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}}},$$
(20)

where I(ρi, z) = W(ρi, ρi, z) (i = 1, 2) stands for the spectral intensity. The position of optical vortex is determined using Eqs. (21) and (22) [34]

$$\text{Re}\left[ {\mu \left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right)} \right]=0,$$
(21)
$$\text{Im}\left[ {\mu \left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right)} \right]=0,$$
(22)

where Re and Im denote the real and imaginary parts of \(\mu \left( {{\varvec{\rho}_1},{\varvec{\rho}_2},z} \right)\), respectively. The sign of optical vortices is determined by the vorticity of phase contours around singularities [35], namely the sign of the topological charge corresponds to plus and minus when the varying phases are in counterclockwise and clockwise directions, respectively.

3 Evolution behavior of mixed screw-edge dislocations

Figure 2 gives curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) and contour lines of phase of mixed screw–edge dislocations beams at the source plane z = 0 and propagating through atmospheric turbulence at the propagation distance z = 0.6, 5 and 8 km. The calculation parameters are λ = 1.06 µm, w = 3 cm, \(C_{n}^{2}\) = 10− 15 m− 2/3, ρ1 = (1 cm, 1 cm) a = 2, b = 1 cm. Figure 2a, e infers that there exists mixed screw-edge dislocations at the source plane z = 0, which is composed of an optical vortex (marked as A) with topological charge + 1 and an edge dislocation (marked as B), the optical vortex A is located at (0, 0). Figure 2b, f indicates that the position of the optical vortex A moves to (–0.02 cm, 1.97 cm), the edge dislocation B evolves into a pair of optical vortices (marked as B+ and B−) with topological charge + 1 and − 1, whose position are located at B+(1.43 cm, − 3.33 cm) and B−(0.59 cm, 4.29 cm) at a propagation distance of z = 0.6 km. Figure 2c, g shows that the position of optical vortices A, B+ and B− continues to move (− 2.85 cm, 6.44 cm), (4.44 cm, 4.11 cm) and (0.67 cm, 16.7 cm), respectively, at z = 5 km. Figure 2d, h infers that the optical vortex A still exists and the pair of optical vortices B+ and B− vanishes at z = 8 km. From Fig. 2 we can know that when mixed screw-edge dislocations beams propagate through atmospheric turbulence, an optical vortex with topological charge + 1 always exists; an edge dislocation evolves into a pair of optical vortices, when the transmission distance is far enough, the pair of optical vortices vanishes.

Fig. 2
figure 2

Curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) and contour lines of phase of mixed screw–edge dislocations beams at the source plane (a, e) z = 0 and at the propagation distance (b, f) z = 0.6 km, (c, g) 5 km and (d, h) 8 km through atmospheric turbulence; empty circles indicates that the topological charge is − 1, and filled circles mean that the topological charge is + 1; the abscissa represents ρ2x direction, the ordinate represents ρ2y direction, and their units are cm

Full size image

Figure 3 gives curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) and contour lines of phase of mixed screw-edge dislocations beams at the source plane z = 0, propagating through atmospheric turbulence at the propagation distance z = 0.6 km, 5 km and 8 km. The calculation parameters are a = − 2. The other calculation parameters are the same as those in Fig. 2.

Fig. 3
figure 3

Curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) and contour lines of phase of mixed screw-edge dislocations beams at the source plane (a, e) z = 0 and at the propagation distance (b, f) z = 0.6 km, (c, g) 5 km and (d, h) 8 km through atmospheric turbulence; empty circles indicate that the topological charge is − 1, and filled circles mean that the topological charge is + 1; the abscissa represents ρ2x direction, the ordinate represents ρ2y direction, and their units are cm

Full size image

Figure 3a, e shows that there exists an optical vortex (marked as C) with topological charge − 1 and an edge dislocation (marked as D) at the source plane z = 0, the optical vortex C is located at (0, 0). From Fig. 3b, f we see that the position of the optical vortex C moves to (− 0.01 cm, − 1.99 cm), the edge dislocation D evolves into a pair of optical vortices (marked as D+ and D−) with the opposite topological charge, whose position is located at D+(0.59 cm, − 4.28 cm) and D−(1.43 cm, 3.35 cm) at z = 0.6 km. Figure 3c, g indicates that the position of optical vortices C, D+ and D− continues move to (–2.98 cm, − 6.01 cm), (0.79 cm, − 15.77 cm) and (4.17 cm, − 4.69 cm), respectively, at z = 5 km. Figure 3d, h shows that the optical vortex C still exists and the pair of optical vortices D+ and D− vanishes at z = 8 km. From Fig. 3 we can know that when mixed screw-edge dislocations beams propagate through atmospheric turbulence, an optical vortex with topological charge − 1 always exists; an edge dislocation evolves into a pair of optical vortices, and the pair of optical vortices vanishes when the transmission distance becomes large enough.

Figure 4 gives the 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z. The calculation parameters of Fig. 4a, b are the same as those in Figs. 2 and 3, respectively. From Fig. 4a, b we can see that when mixed screw-edge dislocations beams propagate through atmospheric turbulence, with the increment of the propagation, the optical vortices A and C always exist; the pairs of optical vortices B+ and B−, D+ and D− annihilate at z = 7.24 and 6.79 km, respectively. Figure 4 shows that when mixed screw-edge dislocations beams propagate through atmospheric turbulence, an optical vortex always exists, and an edge dislocation evolves into a pair of optical vortices; when the transmission distance is far enough, the pair of optical vortices annihilates.

Fig. 4
figure 4

The 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z; filled circles indicate that the topological charge is − 1, and filled circles mean that the topological charge is + 1

Full size image

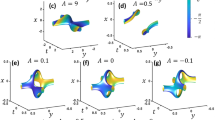
Figure 5 gives the 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z. The calculation parameters are (a, c) a = 2, (b, d) a = − 2, (a, b) \(C_{n}^{2}\) = 2 × 10− 15 m− 2/3 and (c, d) \(C_{n}^{2}\) = 3 × 10− 15 m− 2/3. The other calculation parameters are the same as those in Fig. 2. From Fig. 5a, b we see that the optical vortices A and C always exist and the pairs of optical vortices B+ and B−, D+ and D− annihilate at z = 5.24 and 4.77 km for \(C_{n}^{2}\) = 2 × 10− 15 m− 2/3, respectively. Figure 5c, d indicates that the optical vortices A and C always exist and the pairs of optical vortices B+ and B−, D+ and D− annihilate at z = 4.37 and 3.88 km for \(C_{n}^{2}\) = 3 × 10− 15 m− 2/3, respectively. Figures 4 and 5 show that when mixed screw–edge dislocations beams propagate through atmospheric turbulence, the bigger the refraction index structure constant \(C_{n}^{2}\), the smaller the annihilation distance of a pair of optical vortices.

Fig. 5
figure 5

The 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z; (a, b) \(C_{n}^{2}\) = 2 × 10− 15 m− 2/3 and (c, d) \(C_{n}^{2}\) = 3 × 10− 15 m− 2/3; empty circles indicate that the topological charge is − 1, and filled circles mean that the topological charge is + 1

Full size image

Figure 6 gives the 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z. The calculation parameters are (a, c) a = 2, (b, d) a = − 2, (a, b) b = 1.2 cm and (c, d) b = 1.4 cm. The other calculation parameters are the same as those in Fig. 2. From Fig. 6a, b we can see that the optical vortices A and C always exist and the pairs of optical vortices B+ and B−, D+ and D− annihilate at z = 6.35 and 5.91 km for b = 1.2 cm, respectively. Figure 6c, d indicates that the optical vortices A and C always exist and the pairs of optical vortices B+ and B−, D+ and D− annihilate at z = 5.5 and 5.07 km for b = 1.4 cm, respectively. Figures 4 and 6 show that when mixed screw-edge dislocations beams propagate through atmospheric turbulence, the bigger the off-axis distance of an edge dislocation b, the smaller the annihilation distance of a pair of optical vortices.

Fig. 6
figure 6

The 3D trajectory of optical vortices in atmospheric turbulence versus the propagation distance z; a, b b = 1.2 cm and (c, d) b = 1.4 cm; empty circles indicate that the topological charge is − 1, and filled circles mean that the topological charge is + 1

Full size image

Figure 7 gives curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) of mixed screw–edge dislocations beams at the source plane z = 0, propagating through atmospheric turbulence at the propagation distance z = 1 and 6 km. The calculation parameters are (a–c) a = 2, (d–f) a = − 2 and b = 0 cm. The other calculation parameters are the same as those in Fig. 2. Figure 7a–c indicates that when mixed screw-edge dislocations propagate through atmospheric turbulence, mixed screw-edge dislocations evolve into two optical vortices with topological charge + 1; with the increasing propagation dislocation, two optical vortices spin clockwise. Figure 7d–f show that mixed screw-edge dislocations evolve into two optical vortices with topological charge − 1, two optical vortices spin counterclockwise with increasing propagation distance. From Fig. 7 we can see that when the off-axis distance of an edge dislocation is zero, mixed screw-edge dislocations evolve into two optical vortices with topological charge + 1 or − 1; with the increasing propagation dislocation, two optical vortices spin counterclockwise or clockwise.

Fig. 7
figure 7

Curves of Re µ = 0 (solid curves) and Im µ = 0 (dashed curves) of mixed screw–edge dislocations beams at the source plane (a, d) z = 0 and at the propagation distance (b, e) z = 1 and e, f 6 km through atmospheric turbulence; empty circles indicate that the topological charge is − 1, and filled circles mean that the topological charge is + 1

Full size image

4 Conclusions

By using the extended Huygens–Fresnel principle, taking the mixed screw-edge dislocations beams as an example, the analytical expressions for the cross-spectral density function of mixed screw-edge dislocations beams propagating through atmospheric turbulence have been derived and used to study the evolution behavior of mixed screw-edge dislocations. It is shown that when mixed screw-edge dislocations beams propagating through atmospheric turbulence, the position of an optical vortex varies with the increasing propagation, an edge dislocation evolves into a pair of optical vortices; when the transmission distance becomes large enough, the pair of optical vortices annihilates. The bigger the \(C_{n}^{2}\) and b, the smaller the annihilation distance of the pair of optical vortices. Especially, mixed screw-edge dislocations evolve into two optical vortices with topological charge + 1 or − 1 when the off-axis distance of the edge dislocation b = 0, two optical vortices spin counterclockwise or clockwise with increasing propagation distance. The results obtained have potential applications in optical communications.