High-order harmonic generation in H₂⁺ via multicolor beam superposition: barrier suppression ionization regime

Abstract

Generation of high-order harmonics (HOHs) and attosecond pulses in the barrier suppression ionization regime for a target of hydrogen molecular ion, ${\text{H}}_{2}^{+}$, with large inter nuclear distance is introduced in this work. Some broadband femtosecon laser pulses are designed based on multicolor beam superposition method in order to interact with ${\text{H}}_{2}^{+}$. Behavioral study of harmonics cutoff, attosecond pulse widths and intensities, along with the maximum ionization intensity with respect to the spectral width of driving pulses was carried out. Molecular orbitals in this study are estimated via the linear combination of atomic orbital approximation, and temporal variations of these orbitals are studied in the various ionization regimes. It is seen in this work that although the cutoff harmonic is increased by the driving pulse intensity, but it is insensitive to the spectral driving pulsewidth. This study showed that intensities of the generated attosecond pulses gradually decreased by increasing the bandwidth of the driving laser pulse, but the duration of them is shown to be insensitive in this respect.

1 Introduction

Study around the atomic and molecular dynamics under the exposure of an intense laser pulse (with intensity of more than 10 TW/cm²) has attracted considerable interest in past decades. The two most distinct processes that can take place during this interaction are high-order harmonic generation (HHG) [1] and above threshold ionization (ATI) [2]. Production of the extreme ultraviolet (EUV) attosecond laser pulses from an intense infrared laser by the use of HHG is a breakthrough in the nonlinear optics. However, the first experiments on attosecond pulse generation [3, 4] were performed based on the previous theoretical investigations [1, 5,6,7]. The ionization trends define which phenomenon can take place. Based on the Keldysh rule, the ionization processes in nonlinear optics can be categorized into various phenomena such as tunneling and over-the-barrier ionization for the values of the Keldysh parameter lower than the unity, and multiphoton ionization for mostly higher values of this parameter [8]. HHG is one of the nonlinear effects that can occur under the tunneling or over-the-barrier ionization process. High-order harmonic generation can be described using the so-called simple man’s model. According to this three-step model, the electron (I) is considered to quickly tunnel out through the barrier due to the intense and low frequency laser field, then (II) accelerates freely in the laser electric field while the electric field reverses its motion direction until (III) the electron recombine with the parent ion, and excess of its energy convert to a high energy photon [9, 10]. In the tunneling ionization, the external intense electric field distorts the symmetry of the Coulomb potential well and deforms it to a barrier against the electron, in which it can tunnel out to the free space. But, in the over-the-barrier ionization regime, the strength of the external field is sufficiently high to completely suppress the barrier potential so that the electron can escape the ion freely. The threshold intensity for over-the-barrier ionization, I_b, can be found via a simple study of the distorted soft-core potential under the laser field action. Hydrogen-like atoms with single potential well have a fixed ${I_{\text{b}}}=4 \times {10^9}\frac{{I_{{\text{P}}}^{4}}}{{{{\rm Z}^2}}}$, where I_P is the ionization potential in eV and Ζ is the charge state of the relevant atom. For example for hydrogen atom, ${I_{\text{b}}}=140~\;{\text{TW/c}}{{\text{m}}^2}$, as mentioned in [11]. But in molecules, especially for the simplest ion molecule, i.e., in hydrogen molecular ion (HMI), ${\text{H}}_{2}^{+}$, the threshold intensity for the over-the-barrier ionization depends on the inter-nuclear distance. Besides, the classical cutoff frequency, ω_c, of the harmonic spectrum depends on the incidental laser frequency, ω, and intensity, I, via the relation of ω_c = I_P + 3.17U_P [1], where ${U_{\text{P}}}=I/4{\omega ^2}$ is the ponderomotive energy of the free electron in the external laser field. Thus, it can be predicted classically that the cutoff order of the high-order harmonics (HOHs) extends to higher values by increasing the incidental laser intensity.

Several studies including the experimental measurements [3, 4, 12,13,14,15,16] and theoretical simulations have been carried out on the HHG and attosecond pulse generation [11, 17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. But, ${\text{H}}_{2}^{+}$, and its isotopes are attractive cases to study as simple diatomic molecules. Electron localization and electron dynamics under the Born–Oppenheimer (BO) [11, 22,23,24,25] or non-Born–Oppenheimer (NBO) [26,27,28,29,30,31,32,33,34,35] approximation have been investigated in one [22, 31,32,33,34,35] or three [11, 23,24,25,26,27,28,29,30] dimensional approaches. Molecular orbital (MO) method in the form of linear combination of atomic orbitals (LCAO) mostly used for the theoretical investigations on molecules or molecular ions. The LCAO-MO method was introduced by Lennard-Jones [46], but had been used earlier by Pauling [47] for the ${\text{H}}_{2}^{+}$ ion.

In this paper, we have proposed some especially designed intense multicolor linearly polarized femtosecond pulses via super imposing several continuous wave (CW) beams with frequency difference in the order of δω = 0.005 a.u., in which their intensities are spectrally distributed by a Gaussian function centered at ω₀ = 0.057 a.u. By changing width of the Gaussian distribution, Δω, from 0.01 to 0.04 a.u. several femtosecond driving pulses with various broad spectral pulse-widths can be obtained, which by employing them we can theoretically study the behavior of generated HOHs under the influence of these broadband pulses on the ${\text{H}}_{2}^{+}$. However in this work, the femtosecond driving pulses are designed in the frequency domain because of repeatability, producibility with a few number of beams, and chirp-freeness of designed pulses. Furthermore, in this work, an HMI with an intermediate nuclear separation (R = 10 a.u.) has been considered so as to easily see the vigorous difference between the over-the-barrier and lower-the-barrier ionization. In this research, behavior of the probability density of the wavefunction, ionization probability corresponding to the norm of the remaining wavefunction, populations of the two lowest electronic states of the ${\text{H}}_{2}^{+}$, Harmonics power spectrum and their time–frequency distribution as well as the attosecond pulse train generated from these spectrums have been investigated for the aforementioned values of the pulse peak intensities with respect to the driving pulse spectral width ($\Delta \omega$). It should be noted that time-dependent Schrödinger equation in one dimension (1D-TDSE) under the single active electron (SAE) and Born–Oppenheimer (BO) approximations is employed for the simplicity.

2 Theoretical model

In this article, high-order harmonic generation for a target of hydrogen molecular ion, H₂⁺, is studied in the barrier suppression ionization regime. For this purpose, we produced some multicolor pulses by superimposing many continuous wave (CW) beams coherently. In this section, we present theoretical relations that have been used in this study. The Hartree atomic units (a.u.) are used throughout this article, in which the numerical values of four fundamental physical constants (i.e., m_e, e, ħ, k_e = 1/4πε₀) are all unity.

2.1 Electric field

In this study, an HMI is exposed to an intense and especially designed femtosecond pulse, produced by multicolor beam superposition. These beams are separated spectrally by a constant value of δω in frequency domain. They are all in phase and their linearly polarized electric fields are in the same direction. A Gaussian distribution, F(ω_m), centered at ω₀ = 0.057 a.u. (corresponding to 800 nm) with full width at half maximum (FWHM) Δω has been applied to the amplitudes of the beams. Thus, the final linearly polarized electric field can be written in the following form:

$$E(t)={a_0}\mathop \sum \limits_{{m=1}}^{M} \sin [{\omega _m}(t - {t_0})]F({\omega _m}),$$

(1)

where M is the total number of the beams and ω_m is the m-th beam frequency, and a₀ is a constant to normalize the maximum amplitude of the final electric field to E₀. In the equation above, t₀ is chosen in such a way that the amplitude of the first relative peak in the field becomes less than 0.01 E₀. Consequently, the total time duration is T = 2t₀. Also, in this relation, the Gaussian distribution, F(ω_m), is

$$F({\omega _m})=\exp \left( { - 4\ln 2\frac{{{{({\omega _m} - {\omega _0})}^2}}}{{{{(\Delta \omega )}^2}}}} \right).$$

(2)

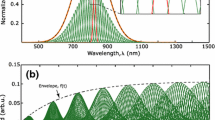
The values for ω_m are taken from 0.012 a.u. (corresponding to 3.8 µm in mid-infrared) to 0.102 a.u. (corresponding to 447 nm in the visible spectrum). Figure 1a shows the Gaussian-distributed intensity magnitudes of contributed beams to produce the final femtosecond pulse. Typical values considered in this figure are Δω = 0.03 a.u. and δω = 0.005 a.u. As it can be seen, the constant number of 19 electric waves is contributed to produce the final electric pulse. But, practically some fewer number of beams concentrated around the center (ω₀ = 0.057 a.u.) are essentially enough to get convergence. However, the objective of this articleis is to investigate the HHG process as a function of the driving pulse bandwidth and intensity. Figure 1b shows the final electric field produced by superimposing these CW beams. As it can be seen in this figure, the generated pulse at the origin is repeated after a certain value of δτ = 6.28/δω. It is one of the advantages of the superposition in the frequency domain in which the generated femtosecond pulse can be repeated periodically as it is shown in Fig. 1b.

Fig. 1

Superposing of 19 electric fields with a constant difference in their frequency, δω = 0.005 a.u., which their amplitudes distributed with a Δω = 0.03 a.u. broadband Gaussian function (a), results in generation of a train of femtosecond pulses by a period of $\delta \tau$ (b). These pulses have a fixed frequency of ω = ω₀ (c) as it is discussed in Eq. (3)

Furthermore, the total number of the beams which are needed to generate the final field is much lower than the previous work [19]. Figure 1c shows the central electric pulse employed in HHG process. Analytically, one can find a compact relation for Eq. (1) given in the following form:

$$E(t)={E_0}\sin [{\omega _0}(t - {t_0})]{{\text{e}}^{ - 4\ln 2\frac{{{{(t - {t_0})}^2}}}{{{{(\Delta T)}^2}}}}},$$

(3)

where ${\omega _0}=({\omega _1}+{\omega _M})/2~$is the central frequency of the spectrum and $\Delta T=\frac{{8\ln 2}}{{\Delta \omega }}$ is the pulse duration. The relation between ΔT and Δω is simply a consequence of time-bandwidth production to describe the pulse duration of a transform limited pulse, based on a certain spectral width. Although we produced a repeating electric pulse upon superposing several CW beams with different frequencies, However, Eq. (3) is only valid for the central pulse (located at t = 0) and is not able to describe another repeated pulses. Consequently, this analitical equation introduces a single driving pulse and allows us to study the behavior of the interaction more easily. Based on the semi-classical Simple Man’s three-step model, strong laser field deforms the coulomb potential of the nucleus and electron can tunnel to the continuum. In this model, the calculations are made by employing the strong field approximation (SFA) and neglecting the ion coulomb field for the propagation of a liberated electron. In addition, the coulomb field is considered as a short range potential, thus, the electron trajectories start at the origin and also electron recombination with ion happens at the origin. Furthermore, in this model, zero velocity is assumed for the electron just in the entrance to the continuum. Classical model can help to understand the electron behavior outside the parent ion. We assume t_i for the electron ionization time and t_r > t_i for its recombination with parent ion. Therefore, the electron velocity, $v(t,{t_{\text{i}}})=\int_{{{t_i}}}^{t} E ({t^\prime }){\text{d}}{t^\prime }$, and trajectory, $r(t,{t_i})=\int_{{{t_i}}}^{t} {\text{d}} {t^\prime }\int_{{{t_i}}}^{{t^{\prime}}} E ({t^{\prime \prime }}){\text{d}}{t^{\prime \prime }}$ in the atomic unit can be obtained. At low frequencies, tunnelling and multiphoton ionization are two competing processes [43].

The Keldysh parameter,$~\gamma =\sqrt {{I_{\text{P}}}/2{U_{\text{P}}}} =\omega \sqrt {2{I_{\text{P}}}} /\varepsilon$, determines the happening ionization process classically, in which $\varepsilon$ is the strength of each electric field that is distributed by $F(\omega )$ in Eq. (2). It can be predicted that for $\gamma <1$ situation, tunnelling ionization is the most probable process, whereas for $\gamma>1$, multi-photon process is dominantly responsible for the ionization. ${U_{\text{P}}}={I_0}/4{\omega ^2}$ is the ponderomotive energy of the electron in the external electric field. Furthermore, the cutoff frequency order in an HHG spectrum can be estimated classically via the relation of ${\omega _{\text{c}}}/\omega =({I_{\text{P}}}+3.17{U_{\text{P}}})/\omega$. Figure 2 shows the classical parameters that can marvelously predict the behavioral effect of the laser field on an atom or a molecule. Ponderomotive energy, cutoff frequency of the HHG power spectrum, and the dimensionless Keldysh parameter are illustrated versus the ingredient frequencies of the generated driving pulse, in this figure. Since the generated pulses finally have a fixed frequency of ω₀ = 0.057 a.u. and have no sign of the chirp effect, delineation of a vertical line at ω₀ = 0.057 a.u. in Fig. 2b predicts the cutoff orders for incidental laser pulses in lower or over barrier ionization regimes. Figure 2c shows that over barrier ionization regime can lay in the tunneling ionization region (γ < 1) but for lower barrier ionization regime (corresponding to ${I_0}<42\;{\text{TW/c}}{{\text{m}}^2}$ enclosed in the orange area) the multi-photon ionization, γ > 1, can be the most probable ionization process. As mentioned above, electron returns to the parent ion at the origin. So, the recollision time ${t_{\text{r}}}$ versus the ionization time ${t_{\text{i}}}$ can be found via solving the following relation:

Fig. 2

a Ponderomotive energy, ${U_{\text{P}}}$, b classical cutoff order, ${\omega _{\text{c}}}/\omega$, and c Keldysh parameter, $\gamma$, for an electric pulse related to Δω = 0.03 a.u., and for typical laser peak intensities of ${I_0}=700~\;{\text{TW/c}}{{\text{m}}^2}$ and ${I_0}=100\;{\text{TW/c}}{{\text{m}}^2}$ in the over-the-barrier ionization region in comparison with ${I_0}=30\;{\text{TW/c}}{{\text{m}}^2}$ in the lower-the-barrier ionization regime, which are respectively illustrated in solid brown, dashed blue, and dash-dotted navy curves. Orange colored areas in these figures represent the lower barrier ionization regions, in which the laser pulse intensity is less than the over barrier ionization threshold, ${I_0}<{I_{\text{b}}}=42\;{\text{TW/c}}{{\text{m}}^2}$. Furthermore, olive rectangle area in c represents the tunneling ionization zone, in which the pulses with the intensities related to this region ionize the target by the tunneling ionization process. It should be noted again that this figure is drawn for an HMI with internuclear distance of R = 10 a.u

$$\mathop \int \limits_{{{t_i}}}^{{{t_r}}} {\text{d}}t\mathop \int \limits_{{{t_i}}}^{t} E(t^{\prime}){\text{d}}t^{\prime}=0,$$

(4)

and one can find the recombination kinetic energy $K({t_{\text{r}}},{t_{\text{i}}})$ of the electron, in atomic units, as follows:

$$K({t_{\text{r}}},{t_{\text{i}}})=\frac{1}{2}{\left[ {\mathop \int \limits_{{{t_i}}}^{{{t_r}}} E(t){\text{d}}t} \right]^2}.$$

(5)

Figure 3 shows the relation between ${t_{\text{r}}}$ and ${t_{\text{i}}}$. From this figure, we can find that for some periods of ionization time, there cannot be found any corresponding recombination time, i.e., if an electron leaves its parent ion at any time during these periods, it will never return again to the ion. These periods of time are colored in light blue (gray) for the case of Δω = 0.030 a.u. On the other hand, there are some instants in which ionized electron has more than one opportunity for returning to the ion. For example for a typical ionization time in the first half cycle (represented by a vertical dached line in Fig. 3), in the case of Δω = 0.030, there can be three recombination times (a, b, c points). Some of the short trajectories (ST) and long trajectories (LT) are also indicated in this figure.

Fig. 3

Recombination time ${t_{\text{r}}}$ versus the ionization time ${t_{\text{i}}}$ in terms of optical cycles. The light blue-colored areas are especially related to the case when Δω = 0.03 a.u. and they are representing never back down temporal regions

2.2 Numerical method for high-order harmonic generation

In this section, we study the effects of these new designed broad-band femtosecond driving pulses on a target of hydrogen molecular ion, ${\text{H}}_{2}^{+}$. For this purpose, we solve the one-dimensional time-dependent Schrödinger equation (1D-TDSE) under the BO and dipole approximations as:

$$\frac{{\partial \psi (z,t)}}{{\partial t}}=\hat {H}\psi (z,t)=[{\hat {T}_z}+U(z,t)]\psi (z,t),$$

(6)

where ${\hat {T}_z}= - \frac{1}{2}\frac{{{\partial ^2}}}{{\partial {z^2}}}$ and $U\left( {z,t} \right)=V\left( z \right)+zE\left( t \right)$. Where z and t are the spatial and temporal components, respectively, and V(z) is the soft-core Coulomb potential,

$$V(z)= - \frac{1}{{\sqrt {{{\left( {z - \frac{R}{2}} \right)}^2}+{\alpha ^2}} }} - \frac{1}{{\sqrt {{{\left( {z+\frac{R}{2}} \right)}^2}+{\alpha ^2}} }},$$

(7)

is introduced for the ion coulomb potential and E(t) is the linearly polarized electric field along the z coordinate discussed in the previous section. Also, α = 1 is a softening parameter to remove the coulomb potential singularity. The split-operator method is used to solve Eq. (6):

$$\psi (z,t+\Delta t) \approx {{\text{e}}^{ - i{{\hat {T}}_z}\frac{{\Delta t}}{2}}}{{\text{e}}^{ - iU(z,t)\Delta t}}{{\text{e}}^{ - i{{\hat {T}}_z}\frac{{\Delta t}}{2}}}~\psi (z,t).$$

(8)

By the use of the calculated wavefunction, we can find other physical quantities of interest such as the population of the ground state ${N_0}(t)$ and norm of the remaining wavepacket $N(t)$ as well as the ionization probability $P(t)=1 - N(t)$. Here, $N(t)$ shows the bound portion of the wavefunction and is not included the ionized parts. Dipole momentum $d(t)$ and acceleration $a(t)$ which induced by the laser field can be used to determine the HHG power spectrum, $\mathcal{S}(\omega )$, time–frequency of the harmonic’s intensity, $\mathcal{W}(\omega ,t)$, and the attosecond pulse train, $\mathcal{I}(t)$ [17, 19].

In this article, we aim to study the effect of these specially designed pulses through the over barrier ionization regime. When the value of external electric field grows enough in such a way that the peak of the barrier becomes lower than the ionization potential, the electron can escape over the barrier. Figure 4 clearly shows that to find the minimum electric field strength, ${E_{\text{b}}}$, which satisfies the over barrier ionization condition; it is sufficient to find a point ${z_{\text{b}}}>R/2~$ in which $\frac{{\partial U}}{{\partial z}}=0$ provided that $U({z_{\text{b}}})= - {I_b}$. Since, in the hydrogen molecular ion, $H_{2}^{+}$, ionization potential, ${I_{\text{p}}}$, depends on the internuclear distance, R, for any electronic states [48, 49]; the discussion above shows that ${E_{\text{b}}}$ depends on R. Also, it can be deduced from this figure that ${E_{\text{b}}}$ values decrease with increasing the internuclear distance. Figure 5 shows ${E_{\text{b}}}(R)$ in $H_{2}^{+}$ for two lowest charge-resonant (CR) pairs of ground state, $1s{\sigma _{\text{g}}}$, and the first excited state, $2p{\sigma _{\text{u}}}$. In oscillation of electric pulse, whenever the absolute value of the electric field exceeds ${E_{\text{b}}}$, over barrier ionization can occur. Figure 6 shows the electron recollision kinetic energy for a typical driving electric pulse with the peak intensity of ${I_0}=7.0 \times {10^{14}}\;{\text{W/c}}{{\text{m}}^2}$ in the over-the-barrier ionization region. In this figure, the recombination kinetic energy of the electron is plotted two times; one is related to the ionization time (ionization profile) and another for the recombination time (recombination profile). Horizontal lines in this figure show ${E_{\text{b}}}$ for ${\text{H}}_{2}^{+}$ when R = 10 a.u. In Fig. 6 for ${E_0}=0.141\;{\text{a.u.}}>{E_{\text{b}}}$, we can observe some periods of time (hachured by orchid) in which $E(t)>{E_{\text{b}}}$. In these regions, over barrier ionization can occur. Also, in this figure, the regions colored in light blue (gray) represent the periods of time in which the ionized electron never come back again to the parent and there is truly no recombination kinetic energy corresponding to the ionization time. Once again we remember that the colored and hachured areas correspond to the ionization time. Although this figure is depicted for a pulse related to the over barrier ionization regime, classical calculations could not differ between the ionization regimes, since trajectory calculations start after the ionization event. Thus, the same behavior for the electron recombination kinetic energy is predicted by the classical calculations in all types of the ionization processes with different values for the electric pulse peak intensities. Furthermore, because of the neglection of all the target characteristics by the approximations, the electron kinetic energy, that obtained by Eq. (5), depends only on the ionization time ${t_{\text{i}}}$ and the behavior of the electric field of the external driving laser pulse. Thus, Fig. 6 cannot recognize the target and is consistent for any target [19, 50]. However, it is predictable from Fig. 2c that the quantum mechanical remarks characterize the differences between these ionization processes as it will be seen in the time–frequency distribution of the harmonics, subsequently.

Fig. 4

Coulomb potential of the ion is sufficiently disturbed by the external laser electric field, E > E_b, in such a way that the bounded electron escapes the ion from top of the barrier

Fig. 5

Minimum strength of laser electric field, E_b, which is needed for the above barrier ionization for the electron lies in the ground state, 1sσ_g, or in the first excited state, 2pσ_u, in an HMI depends on the internuclear distance R

Fig. 6

Classical considerations regarding the recombination kinetic energy of an electron at recollision time, ${t_{\text{r}}}$, affected by an external laser field with the amplitude of ${E_0}=0.141\;{\text{a.u.}}>{E_{\text{b}}}$ in hydrogen molecular ion, ${\text{H}}_{2}^{+}$. The plot is drawn via Eq. (5)

3 Numerical results

As it was mentioned in the previous sections, in this article we have designed an especial set of linearly polarized femtosecond pulses produced by superposing several CW beams. In this study, beams differ by a constant value of δω in their frequency. Furthermore, the amplitudes of these beams are spectrally distributed to a Gaussian function centered at ${\omega _0}$ = 0.057 a.u. (related to ${\lambda _0}$ = 800 nm) and by the FWHM of Δω. Some values of Δω from 0.01 to 0.04 a.u. are used to study the effect of Δω on the final results. Numerical analyses are performed using 1D-TDSE under the dipole and single active electron approximations. To solve the 1D-TDSE numerically, value of dz = 0.05 a.u. and dt = 0.05 a.u. have been taken into account. Width of the spatial coordinate for the electron wavefunction, z, is adjusted to be 200 a.u. for more accuracy. Typical value of Δω = 0.03 a.u. for the FWHM of the incidental laser pulse is chosen for the theoretical considerations. So, the behavior of the involving parameters versus Δω will be studied. Figure 7 again shows a typical driving electric pulse with the peak intensity of 700 TW/cm² which is produced by superposition of 19 beams with frequency difference of δω = 0.005 a.u. from ${\omega _{\text{i}}}$ = 0.012 a.u. to ${\omega _{\text{f}}}$ = 0.102 a.u. In fact, for the most of these pulses, some few numbers of the beams located around the center, ${\omega _0}$, have essential contribution to generate the pulse. However, interaction of these pulses with a hydrogen molecular ion, ${\text{H}}_{2}^{+}$, by the internuclear distance of 10 a.u. is studied here. The initial bound state, ${\psi _0}(z)$, of the ${\text{H}}_{2}^{+}$, supposed to be the ground state, $1s{\sigma _{\text{g}}}$, which is obtained via the LCAO-MO method. In the beginning, Fig. 8 represents the variation of the squared magnitude of electron wavefunction under the influence of three external intense femtosecond laser pulses with the peak intensities of ${I_0}$ = 700 and 100 TW/cm², in over-the-barrier ionization regime, along with the peak intensity of ${I_0}$ = 30 TW/cm², in the lower-the-barrier ionization regime. Figure 9 shows the time-dependent populations of two lowest states of the molecule, i.e., $1s{\sigma _{\text{g}}}$ and $2p{\sigma _{\text{u}}}$, which are obtained from the LCAO-MO method, for three different amplitudes of the laser peak intensities. For this simulation, it is considered that initial population of the first excited state, $2p{\sigma _{\text{u}}}$, to be zero, and it can truly be seen from Fig. 9 that this state is empty at the first time, but it can be occupied and unoccupied frequently in time via electron transfer between this state and the ground state. Occupation rate of the ground state (and consequently first excited state) increases by the driving pulse intensity, where can be seen in Fig. 9 and can be deduced by reviewing Fig. 8, in which we can see that after keeping the electron cloud away from the core, some of the weaker electric pulses are not able to return all of the released part. A small number of electrons transferring between the cores can easily be calculated using normalized probability density of electron in one of the wells:

Fig. 7

A typical electric field representing a 700 TW/cm² femtosecond laser pulse, generated by superposition of a series of Gaussian distributed beams. Spectral width of the pulse is Δω = 0.03 a.u., where the corresponding pulse width results in ΔT = 1.7 OC

Fig. 8

Electronic probability density, P(z, t) = |ψ(z, t)|², of the electron presence in time and space derived by a laser pulse with the width of Δω = 0.03 a.u. for three different laser intensities of a 700 TW/cm², and b 100 TW/cm², in the over-the-barrier, and c 30 TW/cm² related to lower-the-barrier ionization regime

Fig. 9

Populations of the 1sσ_g (solid blue lines) and 2pσ_u (dashed brown lines) states of an HMI corresponding to Δω = 0.03 a.u. for three cases discussed in Fig. 8 as well

$${P_{+\left( - \right)}}(t)=\frac{{|\langle{\varphi _{+\left( - \right)}}|\psi (t)\rangle{|^2}}}{{{{\left| \langle{{\varphi _+}|\psi (t)} \rangle\right|}^2}+{{\left|\langle {{\varphi _ - }|\psi (t)} \rangle\right|}^2}}}$$

(9)

in which, $\psi (t)$ is the time-dependent wavefunction and also $|{\varphi _{+\left( - \right)}}>$ is the steady-state atomic orbital of the hydrogen ground state sitting at R/2 (− R/2). This interchange can also be seen from a delicate inspection of Fig. 8, which is obviously due to oscillation of the field. Figure 10 shows the electron interchange between two wells for three intense laser pulses of the case when Δω = 0.03. Figure 11 shows the norm of the remaining wavepacket, $N(t)$, and the corresponding ionization probability, $P(t)=1 - N(t)$, for two different ionization regimes. By a meticulous comparison with Fig. 3, it can be deduced from Fig. 8 that the released parts of the wavefunction in the no return regions of the ionization time, travel out the window and ionize permanently. So these parts are absolutely ionized and should not be taken into account for the remaining norm, $N(t)$, calculation. Thus, for these calculations we narrowed the spacial widths as much as possible arround the wells. ADK ionization rate in this figure helps to find the sever population depletion instant and the attosecond pulse locations. The figure illustrates that the population depletion rate accelerates when the ADK ionization rate reaches its first peak. Furthermore, mitigation rate of the population corresponding to more intense driving pulse occurs more faster. A simple comparison between the ADK rate in this figure and the electric field of Fig. 7 can shed some light into the matter, because the major strengths of the field lie at its maximum magnitudes, which happens near the mid-time scale.

Fig. 10

Normalized probability density of the electron presence, in the well located at z = R/2, in which Δω = 0.03 a.u

Fig. 11

Norm of the remaining wavepacket, N, and corresponding ionization probability, P, for three driving pulse intensities under the study. In this figure, ADK ionization rate related to these electric fields is also depicted. As it can be seen in the inset, depletion in the electron population occurs in the same magnitude for each ADK peak

The behavior of the total ionization probability, P_max calculated at the end of the pulse, as a function of 1/Δω is depicted in Fig. 12. This figure shows that treatment of the ionization probability with respect to 1/Δω gradually tends to be linear, that is, it can be deduced that maximum ionization probability depends inversely on the spectral pulsewidth (${P_{\rm {max} }}\sim \frac{1}{{\Delta \omega }}$), especially for the weaker pulses related to the intensities of lower-the-barrier ionization regime. Dipole momentum d(t) and acceleration a(t) are two of the most important parameters that can be deduced using the time-dependent electronic wavepacket. Figure 13 clearly shows these two parameters for two aforementioned ionization regimes. HHG spectra are plotted in Fig. 14 for some different values of the spectral width Δω from 0.01 a.u. to 0.04 a.u., and for three different peak intensity values of ${I_0}$ = 700 and 100 TW/cm² in the over-the-barrier ionization regime, and ${I_0}$ = 30 TW/cm², corresponding to the lower-the-barrier ionization regime. For the higher values of $\Delta \omega$, it can be seen that the second cutoff gradually is growing. The classical cutoff expectations (CCE) are also noted for the comparison, which is insensitive to the pulse bandwidth, $\Delta \omega$. From another point of view, we can study the width-frequency (whether spectral, Δω, or temporal, ΔT) distribution of the harmonics. Figure 15 shows the spectral width-frequency distribution of the HOHs generated under the influence of various incidental pulses with many values for spectral (or temporal) widths corresponding to over-the-barrier ionization regime with the peak intensities of ${I_0}=700$ and $100\;{\text{TW/c}}{{\text{m}}^2}$, and lower-the-barrier ionization regime for the peak intensity of ${I_0}=30\;{\text{TW/c}}{{\text{m}}^2}$. As it can be seen in this figure and more clearly in Fig. 16, the cutoff order for the two regimes is almost uniform, except for the large Δω (or equivalently for short pulse duration, ΔT), in which the second cutoff has been raised. Also, in Fig. 16 it is noticeable that the CCE cuts into the actual cutoff. This effect has also been seen in the previous work on the wavelength-distributed beam superposition [19]. Furthermore, Fig. 17 shows the intensity–frequency distribution of the HHG with respect to the intensities from far above the over barrier ionization threshold ${I_0} \gg {I_{\text{b}}}$ to lower-the-barrier ionization region, ${I_0}<{I_{\text{b}}}$, for the case when Δω = 0.03 a.u. This figure shows clearly the increment of the cutoff frequency by increasing the driving laser peak intensity. Additionally, CCE (classical cutoff expectation) is also presented in this figure for justification. Figure 18 shows the time–frequency distribution of the harmonics deduced by the use of the Morlet-wavelet transform of the dipole acceleration. This figure is depicted for three different intensities and for various spectral pulse-widths from (a) Δω = 0.01 a.u. to (d) Δω = 0.04 a.u. In each part, upper plot belongs to the driving pulse with the peak intensity of ${I_0}=700\;{\text{TW/c}}{{\text{m}}^2}$. As it is justified by Fig. 2c, ionization via employing pulses with the peak intensities of these range completely lies in the tunneling ionization region. This means that the ionization by the barrier suppression can be studied similar to the tunnelling ionization. Besides, all the electron behaviors from the ionization to recollision with the parental ion are same as a typical tunnelling ionization process. Central plots in Fig. 18 are related to femtosecond pulses with intensities of about ${I_0}=100\;{\text{TW/c}}{{\text{m}}^2}$ (still in the over-the-barrier ionization regime), and finally lower parts present the time–frequency distributions of HHG via a typical pulse with the intensity lower than the barrier ionization threshold (${I_0}=30\;{\text{TW/c}}{{\text{m}}^2}<{I_{\text{b}}}=42\;{\text{TW/c}}{{\text{m}}^2}$). Figure 2c categorizes these two later cases in the multi-photon ionization due to their Keldysh parameter values that are larger than unity. But for the intermediate case (${I_0}=100~\;{\text{TW/c}}{{\text{m}}^2}>{I_{\text{b}}}$), the barrier suppression process somehow is still responsible for the ionization. So, the ground state electron does not have to absorb any photons to escape from the potential well and, thus, though the Keldysh parameter in this case is greater than 1, ionization and recombination of electron can be studied via the three-step model, same as a tunnelling process. Classical considerations about recollision kinetic energy of an electron with respect to ${t_{\text{i}}}$ or ${t_{\text{r}}}$ that are investigated by Fig. 6 give us the electron trajectories precisely, but are not able to individualize the ionization process. However, meticulous and delicate inspection of the time–frequency distribution of HHG plotted in Fig. 18 shows that for the case of ${I_0}=700~\;{\text{TW/c}}{{\text{m}}^2}$, the electron trajectories are clearly perceivable which confirms that the ionization process behaves completely like a tunneling process. Thus, it can be expected that this driving pulse leads to some sharp attosecond pulses. But for two other weaker pulses, whether in over-the-barrier ionization regime (${I_0}=100\;{\text{TW/c}}{{\text{m}}^2}$) or lower-the-barrier ionization regime (${I_0}=30\;{\text{TW/c}}{{\text{m}}^2}$), the relative indeterminacy of trajectories indicates that in these cases ionization process cannot treat dominantly as a tunneling ionization and it cannot be predicted that some distinct attosecond pulses could be extracted from the interaction of these pulses with an HMI. At the end of this article, attosecond pulse generated due to these interactions can be studied in Figs. 19 and 20. As it is predicted from the ADK ionization rate, there can be some attosecond pulse trains after the exposure of an HMI to intense femtosecond pulses. Figure 19 shows the attosecond pulse train extracted from the interaction of an ${\text{H}}_{2}^{+}$ with the present broadband femtosecond pulses with the FWHM of $\Delta \omega =$ 0.01 to 0.04 a.u. respectively in parts (a)–(d) and with the intensities of ${I_0}=$ 700, 100, and 30 TW/cm² from top to the bottom of each part accordingly. As it can be seen from this figure, the attosecond pulses can be well ordered and clearly distinctive if the initial incidental laser pulse is as intense as possible so much so that it lies deeply in the tunneling ionization region. Although the femtosecond pulse with the intensity of ${I_0}=100\;{\text{TW/c}}{{\text{m}}^2}$ is more intense than the over barrier ionization threshold (${I_{\text{b}}}=42\;{\text{TW/c}}{{\text{m}}^2}\;@\;R=10{\text{ a}}{\text{.u}}.$), it cannot prepare clear trajectories for the released electron (see Fig. 18) and as the middle parts of Fig. 19 show, it cannot lead to some sharp and well-shaped attosecond pulses. This behavior also occurs for the last examined pulse in the lower-the-barrier ionization regime (${I_0}=30\;{\text{TW/c}}{{\text{m}}^2}$). Thus, hereafter, we can discuss the attosecond pulses corresponding to ${I_0}=700\;{\text{TW/c}}{{\text{m}}^2}$. Duration of all pulses in the train is almost equal and as it can be seen in Fig. 19, the pulse duration is about 17 a.s. which is insensitive to Δω. Another remarkable point is regarded as the attosecond pulse intensity with respect to the FWHM of the incidental pulse. Figure 20 shows that the attosecond pulse intensity is decreased gradually by the incidental pulse widths ($\Delta \omega$) or equivalently the attosecond pulse intensities grows by the driving femtosecond pulse durations ($\Delta T$).

Fig. 12

Maximum ionization probability, P_max, calculated at the end of the interaction process versus 1/Δω

Fig. 13

Dipole momentum (a) and acceleration (b) for the case when Δω = 0.03 a.u. for the three various intensities under the study. As it can be seen, dipole momentums and accelerations for these values of intensities are same in the beginning. This similarity also can be seen in the population and/or ionization probability profiles

Fig. 14

HOHs spectra obtained for three incidental pulse intensities of I₀ = 700 TW/cm² (blue solid line), I₀ = 100 TW/cm² (brown solid line) and I₀ = 30 TW/cm² (green-solid line) for some various spectral bandwidth of these pulses from Δω = 0.01 to 0.04 a.u. depicted in a–d, respectively. As it is classically predicted before in Fig. 2b, it can be seen that HOHs cutoff order relating to the more intense driving femtosecond laser pulse is extended to higher values

Fig. 15

Width-frequency distribution for the HOHs generated in the over-the-barrier ionization regime (a, b) and also in the lower-the-barrier ionization regime (c)

Fig. 16

Cutoff order of the harmonics spectrum for I₀ = 700 TW/cm² (upper curves) and I₀ = 100 TW/cm² (middle curves) in the over barrier ionization regime, and for I₀ = 30 TW/cm² (lower curves) in the lower barrier ionization regime. The classical cutoff expectation (CCE) is also presented as horizontal dotted lines for the comparison

Fig. 17

Intensity–frequency distribution of the HOHs generated under the influence of the incidental femtosecond laser pulses with Δω = 0.03 a.u., from below to far above the over-the-barrier ionization threshold. Vertical dashed line identifies the over-the-barrier ionization threshold. CCE calculation is plotted for the comparison

Fig. 18

Time–frequency spectrums obtained from interaction of four different femtosecond laser pulses of Δω = 0.01 a.u. to 0.04 a.u. with an H₂⁺ ion depicted, respectively, in a–d. Spectra related to the over-the-barrier ionization regime are shown in upper part and others, by maintaining the scale, are shown in the lower part of these figures

Fig. 19

a–d Attosecond pulses extracted from interaction process of an HMI (${\text{H}}_{2}^{+}$) with some broadband femtosecond pulses with the spectral width of $\Delta \omega =$ 0.01 to 0.04 a.u., respectively. In these figures, the results related to incidental femtosecond pulses with the intensities of ${I_0}=700,~100,$ and 30 ${\text{TW/c}}{{\text{m}}^2}$ are illustrated in the upper, middle, and lower parts

Fig. 20

Attosecond pulse Intensity versus the spectral width of the initial femtosecond pulse. This figure is related to ${I_0}=700\;{\text{TW/c}}{{\text{m}}^2}$ in the over barrier ionization regime

4 Conclusions

In this article, high-order harmonic generation based on superposing several CW beams was investigated in the over barrier ionization regime. In multicolor beam superposition method, broadband driving laser pulses are formed by superposing numerous CW beams, in which their frequencies differ by a constant value of δω. Such superpositions can be led to some femtosecond driving laser pulses, which interaction of these intense and broadband pulses with a hydrogen molecular ion, ${\text{H}}_{2}^{+}$, led to high-order harmonic generation. Over barrier ionization can be categorized as a tunneling ionization regime regardless of the Keldysh rule. Behavior of the harmonics cutoff, attosecond pulse intensities and widths, with respect to FWHM of driving pulses are done. Time-dependent variations of the molecular orbitals are studied in the over- and lower-the-barrier ionization regimes. In this work, it is concluded that though increasing the intensity of driving pulse leads to increasing the cutoff harmonic order in the HHG spectrum, but the cutoff harmonic was somehow insensitive to the spectral driiving laser pulsewidth. Furthermore, this investigation showed that increasing the incidental pulse width results in decreasing the attosecond pulse intensities slowly, but the attosecond pulse durations were insensitive to the driving femtosecond pulse FWHMs.