1 Introduction

Hyperbolic metamaterials (HMMs) are sub-wavelength-layered metal/dielectric structures whose effective permittivities for different polarizations have different signs [1, 2]. In the past decade, HMMs have rapidly gained a central role in nanophotonics, thanks to their unprecedented ability to access and manipulate the near-field of light emitter or a light scatter [1, 2]. HMMs have shown their extreme aptness and worth-seeing applications in the fields of high-resolution imaging [3], nano-scale waveguiding [4], light confinement [5, 6], exhibiting negative refraction [7, 8], nonlinearity enhancement [5], spontaneous emission engineering [9], thermal emission engineering [10], etc.

On the other hand, slow light effect is an interesting electromagnetic phenomena where the group velocity of light becomes small even approaches zero when light propagates in the strong dispersion media. This phenomena lead to slower speed of light and has aroused a great deal interest due to its potential applications in switching, memory and quantum optics [11, 12], where it is necessary to control the speed of light. Many various engineered structures are proposed to develop the applications based on the slow light effect [12,13,14,15,16,17,18,19,20,21]. Recently, waveguides filled with anisotropic metamaterials cladded by dielectrics or dielectric waveguide cladded by anisotropic metamaterials are demonstrated to investigate the properties of slow light [22,23,24,25,26,27]. These studies show that light can come to complete standstill in anisotropic metamaterial waveguide if the width of the waveguide is tuned to a certain value for a specific frequency or wavelength. For a transverse magnetic (TM) mode, such anisotropic metamaterial can support two different propagation constants, forward and backward. The necessary condition for the complete standstill of light is when these two different forward and backward propagation constants come to a degeneracy point. This degeneracy point means the group velocity of light is zero, which exhibits the phenomena of slow light. However, these studies mainly focus on the effect of HMMs on the properties of slow light while the effect of the cladded dielectric materials is neglected. Actually, different cladded dielectrics may strongly change the properties of slow light. To our best knowledge, the studies of slow light effect using waveguide cladded with arbitrary nonlinear dielectric materials have been less well investigated. Therefore, we have demonstrated four kinds of HMM wavegudies to examine the properties of slow light in this paper. These engineered waveguides are proposed in both asymmetric and symmetric structures. The asymmetric waveguide includes linear–HMM–linear and nonlinear–HMM–linear dielectric structures and the symmetric waveguide includes linear–HMM–linear dielectric structure and nonlinear–HMM–nonlinear dielectric structure. We want to investigate the effect of nonlinearity on the properties of slow light and explore more meaningful results related to slow light because these nonlinear optical devices have the advantage of smaller size and stronger nonlinear effect in metallic structures when compared with usual optical devices.

In this work, the main aim of the paper is to present a analytical study of the characteristics of slow light in a HMM waveguide cladded with arbitrary nonlinear dielectric materials. We wish we may pave a way to the future to fabricate a novel tunable slow light device based on the proposed HMM waveguides. This paper is organized in the following way. In Sect. 2, the model and the corresponding analytical expressions are derived in detail for both asymmetric and symmetric structures. The corresponding numerical results are also discussed with different parameters in Sect. 3. Finally, a short summary is presented in Sect. 4.

2 Theory and formulas

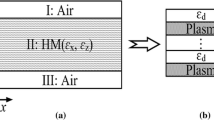
We consider a waveguide made of an anisotropic HMM cladded by dielectric materials with confinement in the xoz-plane, where the schematic diagram is shown in Fig. 1. The HMM is a stack of metal and dielectric with thickness d separating two sides media of two arbitrary dielectric materials that occupy the space of \(z>d\) and \(z<0\), respectively. These two arbitrary dielectric materials can be linear or nonlinear which will be discussed below in detail.

Fig. 1
figure 1

A schematic view of structure considered in this work: the hyperbolic metamaterial waveguide cladded with arbitrary nonlinear dielectric (left) and the hyperbolic metamaterial consists of metal and dielectric periodically (right)

Full size image

Without lost of generality, we consider a TM-polarized wave with the \(\mathbf {H}\) field having y-component only in this work. The electric field at a location in the system can in general be written as

$$\begin{aligned} \mathbf {E}(\mathbf {r},t)=\frac{1}{2}\{iE_{x}(z)\hat{x}+E_{z}(z)\hat{z}\}\exp [i(kx-\omega t)]+c.c., \end{aligned}$$
(1)

where k is the x-component of the wave vector and \(\omega\) is frequency of incident light.

Following Maxwell’s equations \(\nabla \times \mathbf {H}=\partial \mathbf {D}/\partial {t}\) and \(\nabla \times \mathbf {E}=-\mu _{0}\partial \mathbf {H}/\partial {t}\), and fixing the fields \(\mathbf {H}=(0,H_{y},0)\), we can obtain the field amplitudes \(E_{x}(z)\), \(E_{z}(z)\), and \(H_{y}(z)\) in regions 1 and 3 as below:

$$\begin{aligned} \frac{{\text {d}}E_{x}}{{\text {d}}z}= & {} \left( k-\frac{\omega ^{2}}{kc^{2}}\varepsilon _{i}\right) E_{z}, \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\text {d}}(\varepsilon _{i}E_{z})}{{\text {d}}z}= \,& {} k\varepsilon _{i}E_{x}, \end{aligned}$$
(3)
$$\begin{aligned} H_{y}(z)= & {} -\frac{\omega }{k}\varepsilon _{0}\varepsilon _{i}E_{z}. \end{aligned}$$
(4)

Here we consider the general case \(\mathbf {D}=\varepsilon _{i}(E)\mathbf {E}\) [28], where \(\varepsilon _{i}=\varepsilon _{iL}+\alpha _{i}\vert \mathbf {E}\vert ^{\beta }(i=1, 3)\) which denotes the nonlinear dielectric functions in regions 1 and 3, respectively. Here \(\varepsilon _{1, 3L}\) is the linear part of the response, \(\alpha _{1, 3}\) are the nonlinear susceptibilities and are frequency dependent in general, and \(E=\vert \mathbf {E}\vert\). \(\beta\) is the arbitrary nonlinearity, i.e., \(\beta =2\) is a special case for Kerr nonlinear dielectric materials [28]. Especially, \(\alpha _{1, 3}=0\) means that the dielectric materials in regions 1 and 3 are linear. If the dielectric materials in regions 1 and 3 are linear, the dielectric permittivities do not depend on z, and then Eq. (3) reduces to \({\text {d}}E_{z}/{\text {d}}z=kE_{x}\). However, \(\varepsilon _{i}(i=1, 3)\) cannot be canceled in Eq. (3) for nonlinear dielectrics in regions 1 and 3 since the dielectric permittivities depend on z.

The dielectric function of HMM in region 2 is identified by the permittivity tensor with a diagonal form and can be expressed as \(\varepsilon _{2}={\text {diag}}(\varepsilon _{\parallel }, \varepsilon _{\parallel }, \varepsilon _{\perp })\), its diagonal elements have different signs, such as \(\varepsilon _{\parallel }\varepsilon _{\perp }<0\), leading to the hyperbolic dispersion. In our case where the schematic view of structure is shown in Fig. 1, we can get \(\varepsilon _{\parallel }=\varepsilon _{z}\), and \(\varepsilon _{\perp }=\varepsilon _{x}\). Here, as the multi-layer HMM structure is sub-wavelength scaled which means the length of one unit cell consisting of metal and dielectric material is less than the wavelength of light, it could be treated as a homogeneous effective medium and the principal components of the permittivity tensor can be expressed using effective medium approximation [29]:

$$\begin{aligned} \varepsilon _{\parallel }=\, & {} f\varepsilon _{{\text {m}}}+(1-f)\varepsilon _{{\text {d}}}, \end{aligned}$$
(5)
$$\begin{aligned} \varepsilon _{\perp }= & {} \frac{\varepsilon _{{\text {m}}}\varepsilon _{{\text {d}}}}{f\varepsilon _{{\text {d}}}+(1-f)\varepsilon _{{\text {m}}}}, \end{aligned}$$
(6)

where f is the metal filling factor.

The metal discussed in the present paper is described as Drude model and then the corresponding dielectric function can be expressed as \(\varepsilon _{{\text {m}}}=1-\omega _{p}^{2}/\omega ^{2}\), where the \(\omega _{{\text {p}}}\) is plasma frequency which denotes the electron density in the metal. The background dielectric material made from HMM is chosen as glass with the corresponding dielectric constant \(\varepsilon _{{\text {d}}}=2.29\).

The field amplitudes \(E_{x}(z)\), \(E_{z}(z)\), and \(H_{y}(z)\) in region 2 are different from that in regions 1 and 3, which are given by

$$\begin{aligned} \frac{{\text {d}}E_{x}}{{\text {d}}z} = \left( k-\frac{\omega ^{2}}{kc^{2}}\varepsilon _{z}\right) E_{z}, \end{aligned}$$
(7)
$$\begin{aligned} \frac{{\text {d}}(\varepsilon _{z}E_{z})}{{\text {d}}z} = k\varepsilon _{x}E_{x}, \end{aligned}$$
(8)
$$\begin{aligned} H_{y}(z) = -\frac{\omega }{k}\varepsilon _{0}\varepsilon _{z}E_{z}. \end{aligned}$$
(9)
Fig. 2
figure 2

The dielectric function of the hyperbolic metamaterial \(\varepsilon _{z}\) (left) and \(\varepsilon _{x}\) (right) with different filling factors in different frequency regions

Full size image

In the following section, we will derive and present the dispersion relations which are required to examine the properties of slow light in the proposed HMM waveguide. The HMM waveguides have been divided into two conditions: asymmetric and symmetric structures. Two cases will be discussed for each structure in detail.

We first discuss the asymmetric structures where the dielectric materials’ permittivities in regions 1 and 3 are different. The linear–HMM–linear dielectric structure and nonlinear–HMM–linear dielectric structure are considered in this subsection.

2.1 The asymmetric structure: \(\varepsilon _{1}\not =\varepsilon _{3}\)

2.1.1 Linear–HMM–linear dielectric structure

In this case, the dielectric materials in regions 1 and region 3 are different with the corresponding dielectric functions \(\varepsilon _{1}\) and \(\varepsilon _{3}\). Since \(\varepsilon _{i}(i=1, 3)\) is independent of z, Eq. (2) reduces \(dE_{z}/dz=kE_{x}\). Then we can find \(E_{x}(z)\) and \(E_{z}(z)\) in regions 1 and 3 from Eqs. (2)–(4), which can be expressed as:

In region 1 (\(z>d\)),

$$\begin{aligned} E_{x}=\, & {} E_{xd}\exp {[q_{1}(z-d)]}, \end{aligned}$$
(10)
$$\begin{aligned} E_{z}=\, & {} \frac{k}{q_{1}}E_{xd}\exp {[q_{1}(z-d)]}, \end{aligned}$$
(11)

and in region 3 (\(z<0\)),

$$\begin{aligned} E_{x}= \,& {} E_{x0}\exp ({-q_{3}z}), \end{aligned}$$
(12)
$$\begin{aligned} E_{z}= & {} \frac{k}{q_{3}}E_{x0}\exp {(-q_{3}z)}, \end{aligned}$$
(13)

where \(q_{i}=\sqrt{k^{2}-\frac{\omega ^{2}}{c^{2}}\varepsilon _{i}}(i=1, 3)\).

Moreover, in region 2 (\(0<z<d\)), from Eqs. (7)–(9), we also find

$$\begin{aligned} E_{x}= & {} \frac{E_{xd}{\sin }h\,{(q_{2}z)}+E_{x0}{\sin }h\,{[q_{2}(d-z)]}}{{\sin }h\,{(q_{2}d)}}, \end{aligned}$$
(14)
$$\begin{aligned} E_{z}=\, & {} \frac{k\left\{ E_{xd}{\cos }h\,{(q_{2}z)+E_{x0}{\cos }h\,{[q_{2}(d-z)]}}\right\} \frac{\varepsilon _{x}}{\varepsilon _{z}}}{q_{2}{\sin }h\,{(q_{2}d)}}, \end{aligned}$$
(15)

where \(q_{2}=\sqrt{(k^{2}-\frac{\omega ^{2}}{c^{2}}\varepsilon _{z})\frac{\varepsilon _{x}}{\varepsilon _{z}}}\).

Imposing the continuity conditions \(\varepsilon _{z}E_{z0}^{+}=\varepsilon _{3}E_{z0}^{-}\) at the surface \(z=0\) and \(\varepsilon _{z}E_{zd}^{-}=\varepsilon _{1}E_{zd}^{+}\) at the surface \(z=d\), we can obtain the dispersion relation as

$$\begin{aligned} {\tan }h{(q_{2}d)}=-\frac{\frac{\varepsilon _{1}q_{2}}{\varepsilon _{x}q_{1}}+\frac{\varepsilon _{3}q_{2}}{\varepsilon _{x}q_{3}}}{1+\frac{\varepsilon _{1}q_{2}}{\varepsilon _{x}q_{1}}\frac{\varepsilon _{3}q_{2}}{\varepsilon _{x}q_{3}}}. \end{aligned}$$
(16)
Fig. 3
figure 3

Variation of critical width of waveguide for slow light with different dielectric constants of the cladded dielectric materials \(\varepsilon _{3}\); the dielectric constant \(\varepsilon _{1}\) was set to 1 for air

Full size image

2.1.2 Nonlinear–HMM–linear dielectric structure

In this case, we assume the dielectric material in region 1 is nonlinear while in region 3 is linear. The linear region can be treated readily and is similar as mentioned above. The nonlinear dielectric function \(\varepsilon _{1}=\varepsilon +\alpha \vert \mathbf {E}\vert ^{\beta }\) depends on the location. A standard treatment of the nonlinear region 1 invokes a ’first integral’ [30] to obtain an equation for \({\text {d}}E_{x}/{\text {d}}z\). As introduced in Ref. [31], we can obtain the following relation:

$$\begin{aligned} \left( \frac{\omega ^{2}\varepsilon _{1}^{2}}{k^{2}c^{2}}-2\varepsilon _{1}\right) E_{zd}^{2}+\varepsilon E_{d}^{2}+\frac{2\alpha }{2+\beta }E_{d}^{\beta +2}=0. \end{aligned}$$
(17)

Applying the continuity of \(E_{x}\) and \(D_{z}\) across \(z=0\) and \(z=d\), we have \(k\varepsilon _{x}QE_{xd}=q_{2}\varepsilon _{1}PE_{zd}\), where \(Q=\frac{\varepsilon _{3}q_{2}}{\varepsilon _{x}q_{3}}+{\tan }h{(q_{2}d)}\) and \(P=1+\frac{\varepsilon _{3}q_{2}}{\varepsilon _{x}q_{3}}{\tan }h{(q_{2}d)}\). Since \(E_{xd}^{2}+E_{zd}^{2}=E_{d}^{2}\), \(E_{zd}^{2}\) can be solved to give

$$\begin{aligned} E_{zd}^{2}=\frac{k^{2}\varepsilon _{x}^{2}Q^{2}}{k^{2} \varepsilon _{x}^{2}Q^{2}+q_{2}^{2}\varepsilon _{1}^{2}P^{2}}E_{d}^{2}. \end{aligned}$$
(18)

Finally, substituting Eq. (18) into Eq.(17), we can obtain the dispersion relation as

$$\begin{aligned}&\left( \frac{\omega \varepsilon _{1}\varepsilon _{x}}{c}\right) ^{2}Q^{2}-2\varepsilon _{1} \varepsilon _{x}^{2}k^{2}Q^{2}\nonumber \\&\quad +\left(\varepsilon +\frac{2\alpha }{2+\beta }E_{d}^{\beta }\right)\left(k^{2} \varepsilon _{x}^{2}Q^{2}+q_{2}^{2}\varepsilon _{1}^{2}P^{2}\right)=0. \end{aligned}$$
(19)
Fig. 4
figure 4

Variation of critical width of waveguide for slow light with different nonlinearities in the asymmetric structure. The cladded dielectric materials in region 1 were set to air with \(\varepsilon _{1}=1\). The dielectric function of cladded dielectric in region 3 was set to \(\varepsilon _{3}=3.1+\alpha \vert \mathbf {E}\vert ^{\beta }\)

Full size image

Next, we discuss the symmetric structures where the dielectric permittivities in regions 1 and 3 are the same. The linear–HMM–linear dielectric structure and the nonlinear–HMM–nonlinear dielectric structure are considered in this subsection.

2.2 The symmetric structure: \(\varepsilon _{1}=\varepsilon _{3}\)

2.2.1 Linear–HMM–linear dielectric structure

In this case, region 1 and region 3 are the same linear dielectric material; therefore, two possible modes can exist, the odd mode and the even mode. In this paper, we define that a mode is an odd one when \(E_{x}(z)\) is an odd function, and a mode is an even one when \(E_{x}(z)\) is an even function. Our previous work has explored the properties of slow light in a symmetric waveguide filled with hyperbolic metamaterial cladded by linear dielectric material [27]. Therefore, in this paper, we neglect this case.

2.2.2 Nonlinear–HMM–nonlinear dielectric structure

In this case, region 1 and region 3 are the same nonlinear dielectric material. We assume that both the nonlinear dielectric functions as \(\varepsilon _{1, 3}=\varepsilon +\alpha \vert \mathbf {E}\vert ^{\beta }\). As discussed above, there are two modes, the odd mode and even mode, respectively.

For the odd TM mode, the amplitudes \(E_{x}\) and \(E_{z}\) in region 2 can be given as

$$\begin{aligned} E_{x}= & {} \frac{E_{xd}{\sin }h\,{[q_{2}(z-d/2)]}}{{\sin }h\,{(q_{2}d/2)}}, \end{aligned}$$
(20)
$$\begin{aligned} E_{z}= & {} -\frac{k\left\{ E_{xd}{\cos }h\,{[q_{2}(z-d/2)]}\right\} \frac{\varepsilon _{x}}{\varepsilon _{z}}}{q_{2}{\sin }h\,{(q_{2}d/2)}}. \end{aligned}$$
(21)

The continuity of \(E_{x}\) and \(D_{z}\) at the surface \(z=d\) then yields

$$\begin{aligned} -\frac{kE_{xd}{\cos }h\,{(q_{2}d/2)}\varepsilon _{x}}{q_{2}{\sin }h\,{(q_{2}d/2)}} =\varepsilon _{1}E_{zd}. \end{aligned}$$
(22)

Using the relation \(E_{xd}^{2}+E_{zd}^{2}=E_{d}^{2}\) again, we can obtain

$$\begin{aligned} E_{zd}^{2}=\frac{k^{2}\varepsilon _{x}^{2}}{k^{2}\varepsilon _{x}^{2} +\varepsilon _{1}q_{2}{\tan }h{(q_{2}d/2)}}E_{d}^{2}. \end{aligned}$$
(23)

Substituting Eq. (23) into Eq. (17), we can get the dispersion relation for odd TM mode which is given by

$$\begin{aligned} {\tan }h{(q_{2}d/2)}=\left( \frac{\varepsilon _{x}}{q_{2}\varepsilon _{1}}\right) \left( \frac{2k^{2}\varepsilon _{1}-\frac{\omega ^{2}}{c^{2}} \varepsilon _{1}^{2}}{\varepsilon +\frac{2\alpha }{2+\beta }E_{d}^{\beta +2}}-k^{2}\right) ^{1/2}. \end{aligned}$$
(24)

In a similar way above, we easily obtain the dispersion relation for even TM mode as below:

$$\begin{aligned} {\cot }h{(q_{2}d/2)}=-\left( \frac{\varepsilon _{x}}{q_{2}\varepsilon _{1}}\right) \left( \frac{2k^{2}\varepsilon _{1}-\frac{\omega ^{2}}{c^{2}}\varepsilon _{1}^{2}}{\varepsilon +\frac{2\alpha }{2+\beta }E_{d}^{\beta +2}}-k^{2}\right) ^{1/2}. \end{aligned}$$
(25)

Equations (16), (19), and (24), (25) are our main analytical formulas in this paper. In the next section, we will use these four expressions to investigate the properties of slow light. It is worth noting that Eqs. (5) and (6) in Ref. [27] are special cases of the present manuscript. It is convenient to prove that Eqs. (24) and (25) in the manuscript will be simplified to Eqs. (5) and (6) of Ref. [27] when they satisfy the condition \(\varepsilon _{1}=\varepsilon _{3}=1\) used in Ref. [27].

Fig. 5
figure 5

Variation of critical width of waveguide for slow light with different nonlinearity in the symmetric structure. Both the cladded dielectric materials are the same and the dielectric function was set to \(\varepsilon _{1, 3}=3.1+\alpha \vert \mathbf {E}\vert ^{\beta }\)

Full size image

3 Results and discussion

In a follow-up, we numerically investigate the properties of slow light in the HMM waveguide in two situations: (a) asymmetric structures: linear–HMM–linear and nonlinear–HMM–linear cases, and (b) symmetric structures: linear–HMM–linear and nonlinear–HMM–nonlinear cases. All the results are obtained from the dispersion relations based on Eqs. (16), (19) and (24), (25). In the following numerical calculations, we fixed the wavelength of incident light as \(\lambda =632.8\) nm. The filling factor f is chosen as 0.5 and the plasma frequency \(\omega _{\text {p}}\) is chosen as \(3\omega\) except in Fig. 2. Therefore, the dielectric function of the proposed HMM is expressed as \(\varepsilon _{x}=6.4\) and \(\varepsilon _{z}=-2.9\), which is a Type I hyperbolic metamaterial [32]. Moreover, as mentioned in Sect. 1, such proposed HMM waveguide can support both backward and forward propagation constants for each TM mode. The necessary condition for the complete standstill of light is when these two different propagation constants come to a degeneracy point. Therefore, what follows is a discussion of the degeneracy point which can be used to indicate the slow light effect. The degeneracy point is indicated by black dot in Figs. 3, 4 and 5. We also take the \({\text{TM}}_{0}\) mode as the example to examine the properties of slow light in this paper, while other modes have similar behavior as \({\text{TM}}_{0}\) mode.

We first discuss the effect of metal filling factor on the dielectric function of the HMM. Figure 2 shows the dielectric function of the HMM \(\varepsilon _{z}\) and \(\varepsilon _{x}\) with different filling factors in different frequency regions. It is very clear that \(\varepsilon _{z}\) is a smooth continuous function over the whole spectral range starting at positive values for low-frequency regions and decreasing quickly to negative values in the high-frequency regions. On the contrary, \(\varepsilon _{x}\) shows a clear difference. It starts at a positive value then falls quickly to a negative value and then increases to a positive value. These interesting features can significantly control the properties of slow light in the proposed HMM waveguide. Since the metal filling factor can be control tunable, the devices for slow light effect based on the HMM waveguide are actively tunable.

We next show the effect of dielectric permittivities of cladded dielectric materials on the properties of the degeneracy point for the linear–HMM–linear dielectric structure, which is shown in Fig. 3. The cladded dielectric material in region 1 was fixed and set to air with \(\varepsilon _{1}=1\), the other cladded dielectric material in region 3 was set to \({\text{Al}}_{2}O_{3}\) with \(\varepsilon _{3}=3.1\), \({\text{TiO}}_{2}\) with \(\varepsilon _{3}=6.7\), \({\text{CaCO}}_{3}\) with \(\varepsilon _{3}=8.8\), and \({\text{Si}}\) with \(\varepsilon _{3}=11.9\), respectively. It is clear that the width of the HMM waveguide which is required to achieve slow light is significantly changed. Moreover, the width increases with the decreasing of the dielectric constant \(\varepsilon _{3}\). For example, the light stops at width \(d=0.0015\lambda\) for \({\text{Si}}\), at width \(d=0.0032\lambda\) for \({\text{CaCO}}_{3}\), at width \(d=0.0063\lambda\) for \({\text{TiO}}_{2}\), and at width \(d=0.0241\lambda\) for \({\text{Al}}_{2}\text{O}_{3}\). On the basis of these results, we can conclude that choosing different dielectric materials is an optional way to control the properties of slow light in HMM waveguide.

Further, when involved with the nonlinear dielectric materials, the nonlinear effects on the properties of slow light are shown in Figs. 4 and 5, respectively. Figure 4 is plotted for the nonlinear–HMM–linear dielectric structure and Fig. 5 is plotted for nonlinear–HMM–nonlinear dielectric structure. The case of \(\alpha \vert \mathbf {E}\vert ^{\beta }=0\) in both the figures means no nonlinear dielectric material in the cladded materials. It is observed that the nonlinearities significantly change the position of degeneracy point in both asymmetric and symmetric structures, which means the properties of slow light effect can be controlled by adjusting the nonlinearities of the cladded dielectric material. From Fig. 4, it can also be concluded that the critical width of waveguide for slow light decreases which denotes the position of slow light with the increasing of nonlinearities. Therefore, the enhancement of nonlinearities can lead to smaller devices for achieving slow light effect. Such devices are very useful to find novel applications in photonic switch, optical buffers and memory devices replacing current technologies when the smaller devices are indeed needed in future. In Fig. 5, we take both the cladded dielectric materials as nonlinear and have the same dielectric function with \(\varepsilon _{1, 3}=3.1+\alpha \vert \mathbf {E}\vert ^{\beta }\). There are two modes: odd TM mode and even TM mode. Our findings lead us to conclude that these two modes have similar behavior. The critical width of waveguide for slow light increases with the decreasing of the nonlinearity in both modes. Moreover, the critical width in even TM mode is always bigger than in odd TM mode for slow light effect under the same conditions.

4 Conclusions

In this work, we have investigated how nonlinearity changes the properties of slow light in the HMM waveguide. We derived the dispersion relations of light propagating in the proposed HMM waveguide in detail. By calculating the position of the degeneracy point which indicates the occurrence of slow light effect, we have examined the effects of the metal filling factor, cladded dielectric permittivities and nonlinearities on the properties of slow light in both asymmetric (i.e., linear–HMM–linear and nonlinear–HMM–linear cases) and symmetric (i.e., linear–HMM–linear and nonlinear–HMM–nonlinear cases) structures. The results show that the effects significantly change the properties of slow light. Especially, enhancement of nonlinearities of cladded dielectric materials can lead to smaller devices for slow light effect which is required lesser in integrated photonics in the future. Moreover, it is a possible way to achieve the tunable slow light using a HMM waveguide consists of metal and dielectric periodically. However, it should be noted that intrinsic the loss of the HMM materials was neglected in the discussion presented above, which may strongly change the properties of slow light. This idea but impractical assumption was usually employed to approximately predict optical behaviors of plasmonic structures and metamaterials [15]. We believe that the intrinsic loss can change the specific properties but the rules of characteristics of slow light may be unchanged. Moreover, there is a debate on the feasibility of the proposed complete slow light in the HMM waveguides [33]. Therefore, there is still a long way to go to realize the slow light effect in such proposed HMM waveguide. Further researches are needed, especially in the experimental field.