Tunable enhanced Goos–Hänchen shift of light beam reflected from graphene-based hyperbolic metamaterials

Abstract

The tunable and enhanced Goos–Hänchen (GH) shift for TM-polarized reflected beam from the graphene-based hyperbolic metamaterials (GHMM) is theoretically investigated. It is demonstrated that the lateral shift of the reflected beam can be tunable by Fermi energy and thickness of dielectric, and the largest GH shifts can be hundreds of wavelengths due to the enhanced effect by the GHMM. The minimum reflected angle (Brewster angle) moves to larger angle of incidence with the Fermi energy and thickness of dielectric increasing. Numerical simulation results for Gaussian incident beams coincide with the theoretical results from the stationary-phase method. The GH shift from the GHMM, maybe, open a new way for photoelectronic device application in future.

1 Introduction

The Goos–Hänchen (GH) effect shift refers to lateral shift on the interface for different media when a total reflection occurs, which is discovered by Goos and Hänchen [1, 2]. In the last 2 decades, the GH shifts have extensively investigated such as indefinite medium [3], photonic crystals [4], negative refractive media [5], lossless dielectric slab [6], and others. Besides, the manipulation of GH shift is vital for the applications in photoelectric devices. To this end, all kinds of schemes to manipulate the GH shift have been demonstrated. For instance, Wang and Zhu et al. demonstrated the GH shift by coherent control with electric field [7]. Zhao and Gao et al. reported the temperature tunable GH shift on the interface of metal/dielectric composites [8]. Luo et al. proposed the metal-insulator-semiconductor structure to manipulate the GH shift [9].

Graphene, a two-dimensional honeycomb structure, has been shown to possess particular properties [10,11,12]. More importantly, the optical response of graphene is represented by the surface conductivity which can be modulated simply with gate voltage. GH effects in graphene have been discussed in some papers [13,14,15]. Li and Wang et al. present experiment of the GH shift and observe the Giant GH shift in graphene [13]. Wang and Liu et al. reported the GH shifts in graphene asymmetric structure [14]. Jiang et al. presented the electrical tunable GH shift of the transverse magnetic (TM) polarization beam reflected on a graphene-on dielectric surface and found a negative GH shift [15]. In this article, we investigate theoretically the tunable and enhanced Goos–Hänchen (GH) shift for the TM-polarized reflected beam on the graphene-based hyperbolic metamaterials (GHMM) near the Brewster angle.

Hyperbolic metamaterials (HMM) with hyperbolic shape of the dispersion relation have been demonstrated for potential applications in optical waveguide, negative refraction, and imaging hyperlens [16,17,18,19,20,21,22,23,24,25]. Jiao et al. present the design that tunable angle absorption of HMM based on plasma photonic crystals [26]. Xiang et al. reported that the critical coupling can be realized and controlled with GHMM at the near-infrared frequency range [27]. Ning et al. demonstrated a dual-gated tunable absorber by GHMM at the near-infrared frequency range [28]. Considering that graphene has the characteristic behavior of the conductivity as a function of frequency for various chemical potential values, and GHMM has the properties of near-perfect light absorption, in this study, we proposed a GHMM configuration to modulate the lateral shift of the reflected light beam by Fermi energy. By modifying the Fermi energy of the graphene, the conditions of resonance for the GHMM structure are expected to be altered significantly. Therefore, it is anticipated that the GH shift can be easily manipulated by adjusting the Fermi energy. Our theoretical results demonstrate that the GH shift can be hundreds of wavelengths due to the enhanced effect by the GHMM. We believe that the GH shift from the GHMM could open a new way for potential photoelectronic device application in future.

2 Models and methods

2.1 Graphene-based hyperbolic metamaterial

The sheet conductivity of graphene $\sigma$ can be calculated by the Kubo formula [9, 15], and can be denoted as $\sigma ={\sigma _{{\text{intra}}}}+{\sigma _{{\text{inter}}}}$, where the intra-band ${\sigma _{{\text{intra}}}}$ and inter-band ${\sigma _{{\text{inter}}}}$ are given by

$${\sigma _{{\text{intra}}}}=\frac{{i{e^2}{k_{\text{B}}}T}}{{\pi {\hbar ^2}(\omega +{i \mathord{\left/ {\vphantom {i \tau }} \right. \kern-0pt} \tau })}}\left( {\frac{{{E_{\text{f}}}}}{{{k_{\text{B}}}T}}+2\ln \left( {{{\text{e}}^{ - \frac{{{E_{\text{f}}}}}{{{k_{\text{B}}}T}}}}+1} \right)} \right),{\kern 1pt}$$

(1)

$${\sigma _{{\text{inter}}}}=\frac{{i{e^2}}}{{4\pi \hbar }}{\text{ln}}\left| {\frac{{2{E_{\text{f}}}-\hbar (\omega +{i \mathord{\left/ {\vphantom {i \tau }} \right. \kern-0pt} \tau })}}{{2{E_{\text{f}}}+\hbar (\omega +{i \mathord{\left/ {\vphantom {i \tau }} \right. \kern-0pt} \tau })}}} \right|,$$

(2)

where $\omega$ is the incident light frequency, $\hbar$ the Planck constant, ${k_{\text{B}}}$ the Boltzman constant, and $\tau$ the electron–phonon relaxation time. e, T, and ${E_{\text{f}}}$ are an electron charge, the temperature, and Fermi energy, respectively. The effective permittivity ${\varepsilon _{\text{G}}}$ of the graphene sheet is denoted as [9, 15, 27]

$${\varepsilon _{\text{G}}}=1+i\frac{\sigma }{{{d_{\text{G}}}\omega {\varepsilon _0}}},$$

(3)

where ${\varepsilon _0}$ and ${d_{\text{G}}}$ is the permittivity in vacuum and thickness of graphene, respectively.

The effective medium theory is used in the anisotropic GHMM, which has the following uniaxial dielectric tensor components [21, 28]:

$$\varepsilon =\left( {\begin{array}{*{20}{c}} {{\varepsilon _x}}&0&0 \\ 0&{{\varepsilon _y}}&0 \\ 0&0&{{\varepsilon _z}} \end{array}} \right),$$

(4)

where ${\varepsilon _x}={\varepsilon _y}={\varepsilon _\parallel }$ and ${\varepsilon _z}={\varepsilon _ \bot }$. From the effective medium approximations, ${\varepsilon _ \bot }$ and ${\varepsilon _\parallel }$ are the vertical and parallel parts of the permittivity, respectively, and can be written as [27, 28]

$$\begin{gathered} {\varepsilon _\parallel }=\frac{{{d_{\text{G}}}{\varepsilon _{\text{G}}}+{d_{\text{C}}}{\varepsilon _{\text{C}}}}}{{{d_{\text{G}}}+{d_{\text{C}}}}}, \hfill \\ {\varepsilon _ \bot }=\frac{{{\varepsilon _{\text{G}}}{\varepsilon _{\text{C}}}({d_{\text{G}}}+{d_{\text{C}}})}}{{{d_{\text{G}}}{\varepsilon _{\text{C}}}+{d_{\text{C}}}{\varepsilon _{\text{G}}}}}, \hfill \\ \end{gathered}$$

(5)

where ${\varepsilon _{\text{C}}}$ and ${d_{\text{C}}}$ are permittivity of dielectric and thickness of dielectric, respectively. The dispersive surface for TM polarization is deduced by

$$\frac{{k_{z}^{2}}}{{{\varepsilon _x}}}+\frac{{k_{x}^{2}}}{{{\varepsilon _z}}}=k_{0}^{2},$$

(6)

where ${k_0}$ is wave vector in the free space; ${k_x}$ and ${k_z}$ are the wave vector in x and z direction for our structure, respectively. From Eq. (6), the dispersive curve is hyperbolic when ${\varepsilon _x}{\varepsilon _z}<0$, and the graphene-dielectric composite structure is called as GHMM.

2.2 GH shift of the GHMM

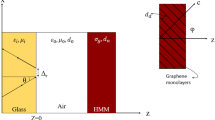
The geometric problem is illustrated in Fig. 1. We assume a GHMM slab in air with the thickness d. A plane wave with incident angle $\theta$ incoming from air into the GHMM slab, the transfer matrix for the GHMM slab can be denoted as [27, 28]

Fig. 1

Schematic diagram of light beam propagating through a GHMM in air

$$\left[ {\begin{array}{*{20}{c}} {\cos ({k_{2z}}d)}&{\frac{{ip}}{{{k_{2z}}}}\sin ({k_{2z}}d)} \\ {i\frac{{{k_{2z}}}}{p}\sin ({k_{2z}}d)}&{\cos ({k_{2z}}d)} \end{array}} \right],$$

(7)

where $p={{{\varepsilon _x}} \mathord{\left/ {\vphantom {{{\varepsilon _x}} {{\varepsilon _1}}}} \right. \kern-0pt} {{\varepsilon _1}}}$ and ${k_{2z}}={{{\omega ^2}} \mathord{\left/ {\vphantom {{{\omega ^2}} {{c^2}}}} \right. \kern-0pt} {{c^2}}}({\varepsilon _y} - {\varepsilon _1}{\mu _1}{\sin ^2}\theta )$for TM polarization.

Then, the reflection coefficient r for TM-polarized incident beam can be obtained by the transfer matrix method:

$$r(d,\theta )=\frac{{{{ - i\sin ({k_{2z}}d)(pk_{{1z}}^{2} - {{k_{{2z}}^{2}} \mathord{\left/ {\vphantom {{k_{{2z}}^{2}} p}} \right. \kern-0pt} p})} \mathord{\left/ {\vphantom {{ - i\sin ({k_{2z}}d)(pk_{{1z}}^{2} - {{k_{{2z}}^{2}} \mathord{\left/ {\vphantom {{k_{{2z}}^{2}} p}} \right. \kern-0pt} p})} {(2{k_{1z}}{k_{2z}})}}} \right. \kern-0pt} {(2{k_{1z}}{k_{2z}})}}}}{{{{\cos ({k_{2z}}d) - i\sin ({k_{2z}}d)(pk_{{1z}}^{2}+{{k_{{2z}}^{2}} \mathord{\left/ {\vphantom {{k_{{2z}}^{2}} p}} \right. \kern-0pt} p})} \mathord{\left/ {\vphantom {{\cos ({k_{2z}}d) - i\sin ({k_{2z}}d)(pk_{{1z}}^{2}+{{k_{{2z}}^{2}} \mathord{\left/ {\vphantom {{k_{{2z}}^{2}} p}} \right. \kern-0pt} p})} {(2{k_{1z}}{k_{2z}})}}} \right. \kern-0pt} {(2{k_{1z}}{k_{2z}})}}}},$$

(8)

where ${k_{1z}}=({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0pt} c})\sqrt {{\varepsilon _1}{\mu _1}} \cos \theta$. The reflection phase ${\phi _r}$ can be denoted as follows:

$$r=\left| r \right|\exp (i{\phi _r}).$$

(9)

If the incident ray is a sufficiently large beam waist (i.e., an angular spectrum of beam is very narrow), the lateral shifts which was proposed with the stationary-phase method [3,4,5] can be described by

$$s= - \frac{\lambda }{{2\pi }}\frac{{{\text{d}}{\phi _r}}}{{{\text{d}}\theta }},$$

(10)

where $\lambda$ is the wavelength in the air.

3 Results and discussion

3.1 The tunable GH shift in GHMM

Figure 2a, b shows the real part of effective permittivity ${\varepsilon _z}$ and ${\varepsilon _x}$, respectively, with different Fermi energies in near-infrared frequency. The Fermi energies of graphene is assumed ${E_{\text{F}}}$ =0.2, 0.38, and 0.4 eV. The other parameters are T = 300 K, $\tau$ = 100 fs, d_C = 8 nm, ${\varepsilon _{\text{c}}}$= 14.3, d_G = 0.35 nm. The real part of ${\varepsilon _z}$ is always positive for all wavelength of interest, and varies slowly with the wavelength increasing while decreased slightly with the Fermi energy increasing. However, the real of ${\varepsilon _x}$ appears resonant behavior at near-infrared frequency. For E_f = 0.4 eV, the resonant wavelength $\lambda$ = 1553 nm, at the frequency, ${\text{Re}}({\varepsilon _x}){\text{Re}}({\varepsilon _z})<0$. From Eq. (6), the dispersive curve is hyperbolic when${\text{Re}}({\varepsilon _x}){\text{Re}}({\varepsilon _z})<0$, and this graphene-dielectric layered structure is called as GHMM. Furthermore, the resonant condition of ${\varepsilon _x}$ can be controlled by increasing Fermi energy. If the Fermi energy increases, the resonant wavelength $\lambda$ has a blue shift.

Fig. 2

a Real part of ${\varepsilon _z}$ versus wavelength for different Fermi energies E_f. b Real part of ${\varepsilon _{\text{z}}}$ versus wavelength for different Fermi energies ${E_{\text{f}}}$

The electrically controlled resonance wavelength provides a way to adjust the reflectivity, reflection phase, and GH shift, as shown in Fig. 3a–c, respectively. From Fig. 3a, it can be found that the reflectivity is greatly reduced with the Fermi energy increasing. At the same time, the minimum reflected angle (Brewster angle) moves to larger angle of incidence. From Fig. 3c, it can be found that the GH shift is large negative close to the Brewster angle, and largely enhanced with the Fermi energy increasing. When Fermi energy E_f = 0.4 eV, the GH shift $S= - 163\lambda$ can be obtained. It can be explained from Fig. 3b that the slope of the reflection phase increases with Fermi energy increasing for the incident angle. Hence, the GH shift enhanced with Fermi energy increasing.

Fig. 3

Dependence of the reflectivity (a), reflection phase (b), and GH shift (c) on the incident angle at different Fermi energies E_f, respectively. Here, $\tau =100$ fs, T = 300 k, d_C = 8 nm, $\lambda =1553\;{\text{nm}}$

3.2 Influence of structure parameter

From Eq. (5), we can find that the thickness of dielectric C is an important parameter, since the effective permittivity of GHMM is strongly dependent on d_c. Figure 4a–c shows the reflectivity, reflection phase, and GH shift for incident angle with various values of d_c, respectively. It is obvious that the reflectivity is urgently reduced with d_c increasing and the absolute of GH shifts are remarkably enhanced with increasing d_c, which is due to the slope of the reflected phase increasing, as shown in Fig. 4b. The negative GH shift is enhanced to $S= - 300\lambda$ for d_c = 15 nm, as shown in Fig. 4c. Hence, the thickness of dielectric C played a key role for the GH shift close to the Brewster angle.

Fig. 4

Dependence of the reflectivity (a), reflection phase (b), and GH shift (c) on the incident angle for different thickness of dielectric C, respectively. Here, E_f = 0.4 eV; other parameters are the same as in Fig. 3

3.3 Gaussian-shaped probe beam simulations of GH shift

In the above analysis, the results of calculation are based on the stationary-phase method [6,7,8,9], for which incident electromagnetic wave is supposed to be a collimated beam. In reality, the Gaussian probe beam is a finite width. When an incident probe beam of Gaussian shape passes through the GHMM structure, the electric field of the incident beam is represented by [9, 15, 29]

$$E_{x}^{{{\text{in}}}}\left| {_{{z=0}}={{({1 \mathord{\left/ {\vphantom {1 {2\pi }}} \right. \kern-0pt} {2\pi }})}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right.\int {A({k_y})\exp (i{k_y}y){\text{d}}{k_y}} ,$$

(11)

where $A({k_y})=({w_y}/\sqrt 2 )\exp [ - w_{y}^{2}{({k_y} - {k_{y0}})^2}/4]$is the beam of Gaussian shape in the angle of incidence $\theta$, ${w_y}={W \mathord{\left/ {\vphantom {W {\cos \theta }}} \right. \kern-0pt} {\cos \theta }}$, ${k_{y0}}=k\sin \theta$, and W is the waist width of beam.

Hence, the reflected electric field of probe beam can be represented by the following [9, 15, 29]:

$$E_{x}^{r}\left| {_{{z=0}}={{({1 \mathord{\left/ {\vphantom {1 {2\pi }}} \right. \kern-0pt} {2\pi }})}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right.\int {r({k_y})} A({k_y})\exp (i{k_y}y){\text{d}}{k_y}.$$

(12)

For the probe beam of Gaussian-shape, the lateral shift is represented by the following [9, 29]:

$$S=\frac{{\int\limits_{{ - \infty }}^{{+\infty }} {{{\left| r \right|}^2}} {A^2}\frac{{\partial {\varphi _r}}}{{\partial {k_y}}}{\text{d}}{k_y}}}{{\int\limits_{{ - \infty }}^{{+\infty }} {{{\left| r \right|}^2}{A^2}{\text{d}}{k_y}} }},$$

(13)

Figure 5a, b shows the numerical simulation of Gaussian-shaped probe beam for the TM polarized from the GHMM for different incident angles with the width of probe beam $W=40\lambda$. Figure 5a shows the case of $\theta ={74.25^ \circ }$, and we can find that the reflected beam is a double-peak contour, which consist with Refs. [2, 29]. The double peak appears owing to the lateral shift larger than the incident beam width. Figure 5b is plotted at the incident angle $\theta ={75^ \circ }$, in which the lateral shift is negligible. The detailed explanations for the reflected light beams for different incident angle can be found in [2].

Fig. 5

Numerical simulations of the reflected beam (red curve) and incident beams (blue curve) shown as the field amplitude versus y-coordinate for the incident angle of a $\theta ={74.25^ \circ }$and b $\theta ={75^ \circ }$. Here, $W=40\lambda$, other parameters are the same as in Fig. 3

Figure 6a, b shows the lateral shift calculated by Eq. (13) with different probe beam width for different Fermi energy and thickness of dielectric C, respectively. It is evident that the numerical simulations results of Gaussian-shaped probe beam coincide with the results from the stationary-phase method, while the wide of probe beam waist is sufficiently large. The discrepancy just appears, while the lateral shift is larger than the width of the incident probe beam (see Fig. 5a).

Fig. 6

Lateral shifts versus beam half-width W under different Fermi energies ${E_{\text{f}}}$ for a and different thickness of dielectric C for b

4 Conclusion

In summary, the GH shift of the TM polarization beam reflected form the GHMM is theoretically investigated. It is found that the GH shift can be tuned through Fermi energy and thickness of dielectric, and the GH shifts can be enhanced to hundreds of wavelength due to the resonant effect. The minimum reflected angle moves to larger angle of incidence with the Fermi energy and thickness of dielectric increasing. The theoretical results from the stationary-phase method are reasonable agreement with the numerical simulation. The GH shift from the GHMM may be interesting for potential photoelectronic device application in future.