1 Introduction

The nonlocal nonlinearity demonstrates a lot of novel properties, such as it can suppress the collapse of (1 + 2)-dimension solitons [1, 2], support the propagation of multipole solitons [3, 4], and provide the attractive force between two optical solitons [5,6,7,8]. Therefore, many scholars have paid attention to it and achieved a series of research results, for example, nonlocal dark soliton [9, 10], nonlocal Bragg soliton [11], ring dark and antidark solitons [12], nonlocal gap soliton [13], elliptic optical soliton [14], Hermite–Gaussian soliton [15], incoherent nonlocal solitons [16], quadratic soliton [17,18,19,20], X-wave [21] and Airy-Gaussian beam [22] in nonlocal media, etc.

The optical beams which are carrying OAM have attracted much attention for that they can exert forces and torques on the microparticles. In fact, the applications of technologies associated with OAM range from optical tweezers to microscopy. Some optical solitons with OAM have been found to be in nonlocal media, such as vortex soliton [23], Laguerre–Gaussian soliton (azimuthal number m ≠ 0) [24], Ince–Gaussian vortex soliton [25], spiraling elliptic optical soliton [26], and spiraling elliptic Hermite–Gaussian soliton [27]. This paper introduces the SELG soliton, which has more complicated structures in its profile and phase compared with the spiraling elliptic Hermite–Gaussian soliton and conventional Laguerre–Gaussian soliton, and can rotate during propagation.

On the other hand, the current researches are mainly focusing on the nonlocal Kerr nonlinearity. In the recent years, the competing nonlocal nonlinearity has been found in the reality materials, for instance, it occurs naturally in Bose–Einstein condensates for the simultaneous local and long range bosonic interaction [28], and in nematic liquid crystals for the comparable thermal and orientational nonlinearities [29]. In addition, some scholars have proved that it has some novel characteristics [30, 31], such as Ref [32] revealed that the suitable competing effects support the stable vortex solitons with topological charge m > 2, as well as one-dimensional multi-hump solitons with number of humps p > 4, all of which are highly unstable in natural nonlocal materials with focusing nonlinearities. Q. Wang demonstrated that the competing nonlocal nonlinearity may drastically affect the interactions of dark solitons [33]. Hence, the study on the propagation of SELG in nonlocal competing CQ nonlinear media should have some new discoveries and actual significances.

2 Theoretical model

The propagation of an optical beam in (1 + 2)-dimensional nonlocal nonlinear media with competing CQ nonlinearities is modeled by the following normalized nonlocal nonlinear equations [30,31,32,33]

$$i\frac{{\partial \psi }}{{\partial z}}+\frac{1}{2}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}}+\frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)\psi +({\alpha _3}{n_3}+{\alpha _5}{n_5})\psi =0$$
(1a)
$${n_3}=\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{R_3}(x - {x^\prime },y - {y^\prime }{{\left| {\psi ({x^\prime },{y^\prime },z)} \right|}^2}{\text{d}}{x^\prime }{\text{d}}{y^\prime }} } ,$$
(1b)
$${n_5}=\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{R_5}(x - {x^\prime },y - {y^\prime }){{\left| {\psi ({x^\prime },{y^\prime },z)} \right|}^4}{\text{d}}{x^\prime }{\text{d}}{y^\prime }} } ,$$
(1c)

where ψ represents the slowly varying envelope, z is the propagation axis, x and y stand for the transverse directions. α3 and α5 are the cubic and quintic nonlinear coefficients, respectively. R3 and R5, which are the nonlocal response functions, were set as the symmetrical Gaussian-shaped as follows,

$${R_3}(x,y)=\frac{1}{{\pi \sigma _{3}^{2}}}\exp \left[ { - \frac{{{x^2}+{y^2}}}{{\sigma _{3}^{2}}}} \right],$$
(2a)
$${R_5}(x,y)=\frac{1}{{\pi \sigma _{5}^{2}}}\exp \left[ { - \frac{{{x^2}+{y^2}}}{{\sigma _{5}^{2}}}} \right],$$
(2b)

where σ3,5 are the characteristic lengths of the response functions. It is well-known that the Gaussian is a non-physical response function [34]. The more physical response function is exponential-decay shaped, and periodic function sin(|x|/σ) [35], etc. However, the solution of the NNLSE can be obtained conveniently using Gaussian-shaped response function and the physical properties do not depend strongly on the concrete shape of the response function. The SELG solution to Eq. (1a) with azimuthal number m and radial number p was introduced as follows

$$\begin{gathered} \psi (x,y,z)=A(z){({X_2}+{Y_2})^{m/2}}L_{p}^{m}[{(X+iY)^2}]\exp \left[ { - \frac{{{X^2}}}{{2{b^2}(z)}} - \frac{{{Y^2}}}{{2{c^2}(z)}}} \right] \hfill \\ \exp (im\varphi )\exp [iB(z){X^2}+i\Theta (z)XY+iC(z){Y^2}+i\theta (z)] \hfill \\ \end{gathered}$$
(3)

where A(z) is the amplitude, L p m[(X + iY)2] represents the Laguerre polynomial. X = xcosωz + ysinωz, Y = − xsinωz + ycosωz, X and Y are rotating coordinates, ω is the angular velocity. φ = arctan(Y/X) is the azimuthal angle, B(z) and C(z) represent the phase-front curvatures in X and Y directions, respectively, Θ(z) stands for the cross-term phase coefficient, and θ(z) is the phase of complex amplitude.

The optical power and OMA can be obtained by inserting Eq. (3) into the following two equations, respectively [26, 27]

$$P=\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{{\left| {\psi (x,y)} \right|}^2}{\text{d}}x{\text{d}}y} } ,$$
(4a)
$$M=\operatorname{Im} \int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{\psi ^*}\left( {x\frac{{\partial \psi }}{{\partial y}} - y\frac{{\partial \psi }}{{\partial x}}} \right){\text{d}}x{\text{d}}y} } .$$
(4b)

According to definition of the second-order moment for beam width, the widths of initial SELG beam are [24]

$${b_{{\text{pm}}}}=\sqrt {\frac{{2\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{x^2}} } {{\left| {\psi (x,y)} \right|}^2}{\text{d}}x{\text{d}}y}}{{\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{{\left| {\psi (x,y)} \right|}^2}{\text{d}}x{\text{d}}y} } }}}$$
(5a)
$${c_{{\text{pm}}}}=\sqrt {\frac{{2\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{y^2}} } {{\left| {\psi (x,y)} \right|}^2}{\text{d}}x{\text{d}}y}}{{\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{{\left| {\psi (x,y)} \right|}^2}{\text{d}}x{\text{d}}y} } }}}$$
(5b)

The ellipticity of the SELG optical beam and the degree of the nonlocality can be expressed as follows [26, 27]

$$\eta =b/c$$
(6a)
$${\delta _{3,5}}={\sigma _{3,5}}/{b_{{\text{pm}}}}$$
(6b)

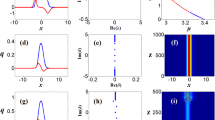
Figure 1 depicts the normalized profiles of the SELG beams in x-direction. The comparison of Fig. 1a–c shows that, when the order increases, the distribution of light field becomes more complex. Such as the red lines (c = 1 and b = 1.1) show that, in the x-direction, the (0, 3), (1, 1) and (2, 1)-order SELG beams have two, four, and six peaks, respectively. Furthermore, the distribution of light field varies with the change of ellipticity. For convenience, first of all, this paper will study the propagation properties of the SELG beams with different orders in nonlocal cubic nonlinear media and different ellipticity in nonlocal quintic nonlinear media, respectively. And, then investigate the effect of nonlocal competing CQ nonlinearities on the propagation of the SELG beam.

Fig. 1
figure 1

Normalized profiles of SELG beams in x-direction. The parameters are chosen as c = 1, b = 1.1, 1.5 and 2 for red, blue and purple lines, respectively. The orders are a p = 0, m = 3, b p = 1, m = 1, and c p = 2, m = 1

Full size image

3 Numerical result

We use the split-step Fourier method to simulate the beam propagation. Obviously, the smaller the step size, the more accurate the result is. The number of points in the transverse x-direction and propagation direction are 512 and 1024, respectively.

3.1 In nonlocal cubic nonlinear media (α 3 = 1, α 5 = 0)

The propagation dynamics and initial phase structures of the SELG solitons with different orders in nonlocal cubic nonlinear media are shown in Figs. 2 and 3, respectively. By comparing the Fig. 1a–c, we can find that, the different-order SELG solitons with the same ellipticity, have the same rotation period (T) and cross-term phase coefficient Θ(z), in addition, the critical power of that is nearly unchanged, which can be clearly observed in Fig. 4a. However, the OAM increases obviously as the order increases. This is because the OAM is related to the beam width. Figure 5 shows that, the higher the order of the soliton, the larger the beam width is.

Fig. 2
figure 2

Propagation of SELG solitons with different orders in nonlocal cubic nonlinear media. The parameters are all chosen as b = 1.5, c = 1, Θ = 0.278, σ3 = 20, a p = 0, m = 1, P01 = 137,500, M01 = 205,000, b p = 0, m = 2, P02 = 141,000, M01 = 412,000, c p = 1, m = 2, P12 = 145,400, M12 = 817,000

Full size image
Fig. 3
figure 3

Initial phase structures of the SELG solitons with different orders. The parameters are all chosen as Fig. 2

Full size image
Fig. 4
figure 4

The critical powers (a) and OAMs (b) of SELG solitons with different orders. The parameters are chosen as b = 1.5, c = 1, Θ = 0.278, σ3 = 20, α3 = 1, α5 = 0. p = 0, 1, 2 correspond to red, blue and purple lines, respectively

Full size image

Besides, the comparison of Fig. 5a–c shows that, the stability of SELG soliton decreases as the order increases. The difference of intensity distributions between the input SELG solitons (black lines) and the output ones (green lines) is so small that one can hardly distinguish it in Fig. 5a, b. However, the difference of that becomes bigger when p = 1, m = 2 in Fig. 5c. Which means that it is the quasi-stable soliton state in Fig. 2c.

Fig. 5
figure 5

Intensity distributions of the SELG solitons for propagation time t = 0 (black lines) and t = 3T (green lines). The parameters are all chosen as Fig. 2

Full size image

3.2 In nonlocal quintic nonlinear media (α 3 = 0, α 5 = 1)

Figure 6 displays the propagation of SELG solitons with different ellipticity in nonlocal quintic nonlinear media with the same degree of nonlocality. In fact, the initial phase structure (as shown in Fig. 7) and intensity distributions (as shown in Fig. 9) of the SELG solitons are different for the different ellipticity. Our simulations have demonstrated that, with the increase of ellipticity, the rotation period (T), cross-term phase coefficient Θ(z), critical power and OAM are all increased, as seen in Figs. 6 and 8. These numerical results are the same as the counterpart of the ground mode which was studied in Ref [26]. In addition, the rotation period slightly increases during propagation. Such as in Fig. 6c, the 1T and 3T at the propagation distance z = 10 and 30.4, respectively.

Fig. 6
figure 6

Propagation of SELG solitons with different ellipticity in nonlocal quantic nonlinear media. The parameters are chosen as δ5 = 10, p = 1, m = 0, c = 1, a b = 1.2, b10 = 1.83, σ5 = 18.3, P10 = 1533, M10 = 2413, Θ = 0.15, b b = 1.5, b10 = 2.76, σ5 = 27.6, P10 = 3771, M10 = 9527, Θ = 0.28, c b = 2, b10 = 4.22, σ5 = 42.2, P10 = 15,000, M10 = 73,186, Θ = 0.38

Full size image
Fig. 7
figure 7

Initial phase structures of the SELG solitons with different ellipticity. The parameters are all chosen as Fig. 5

Full size image
Fig. 8
figure 8

The critical power (red line) and OAM (blue line) of SELG soliton versus the ellipticity. The parameters are chosen as p = 1, m = 0, c = 1, δ5 = 10

Full size image
Fig. 9
figure 9

Intensity distributions of the SELG solitons for propagation time t = 0 (black lines) and t = 3T (green lines). The parameters are all chosen as Fig. 6

Full size image

By comparing the Fig. 9a–c, we found that the stability of SELG soliton decreases as the ellipticity increases. In Fig. 9a, b, the completely stable solitons are formed. In Fig. 9c, the intensity distribution of the SELG beam slightly changes. It is implied that there is only quasi-stable soliton in Fig. 6c.

3.3 In nonlocal competing CQ nonlinear media

For nonlocal competing CQ nonlinear media, first of all, we consider the nonlocal self-focusing cubic and self-focusing quintic nonlinear case, i.e., α3 > 0 and α5 > 0. Figure 10 shows the propagation of the SELG beam in this media. For that, the difference of intensity distributions between the input SELG solitons (black lines) and the output ones (green lines) is so small in Fig. 11, we deem that the stable soliton can be formed.

Fig. 10
figure 10

Propagation of the SELG solitons in nonlocal competing CQ nonlinear media. The parameters are chosen as p = 2, m = 0, b = 1.4, b20 = 3.18, c = 1, σ3 = σ5 = 31.8, δ3 = δ5 = 10, α3 = 1, α3 = 0.001, P10 = 196,570, M10 = 830,000

Full size image
Fig. 11
figure 11

Intensity distributions of the SELG solitons for propagation time t = 0 (black lines) and t = 3T (green lines). The parameters are all chosen as Fig. 10

Full size image

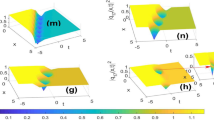
Since the cubic nonlinearity is directly proportional to |ψ|2, and the quintic nonlinearity is directly proportional to |ψ|4, when the quintic nonlinear coefficient α5 increases, a smaller critical power can induce large enough nonlinear effect to balance the diffraction effect. Therefore, the critical power and OAM of a completely stable SELG soliton both decrease as seen in Fig. 12.

Fig. 12
figure 12

The critical power (red line) and OAM (blue line) of SELG soliton versus the quintic nonlinearity coefficient α5. The parameters are chosen as p = 2, m = 0, b = 1.4, b20 = 3.18, c = 1, σ3 = σ5 = 31.8, δ3 = δ5 = 10, α3 = 1

Full size image

However, when the degree of nonlocality δ5 increases, as shown in Fig. 13, the critical power and OAM of a completely stable SELG soliton both increase too. This is due to the fact that the nonlocality can effectively decrease the strength of the nonlinearity, the stronger the nonlocality, the weaker the nonlinearity is. We should increase the initial power to increase the nonlinear effect until it can balance the diffraction effect. And, then the increase of critical power will lead to the increase of angular momentum.

Fig. 13
figure 13

The critical power (red line) and OAM (blue line) of SELG soliton versus δ5. The parameters are chosen as p = 2, m = 0, b = 1.4, b20 = 3.18, c = 1, σ3 = 31.8, δ3 = 10, α3 = 1, α5 = 0.001

Full size image

When α3 > 0 and α5 < 0, this is the nonlocal media with self-focusing cubic and self-defocusing quintic nonlinearities.

Figure 14 shows that, due to the competing effect between cubic and quantic nonlinearities, the bistable SELG solitons, which have the same beam widths and rotation periods (T), but carrying larger or smaller powers as well as OAMs, can be formed in this media. By comparing Fig. 15a, b, we can found that the stability of soliton in Fig. 14a is a bit better than that of soliton in Fig. 14b.

Fig. 14
figure 14

The propagation dynamics of bistable SELG solitons in nonlocal competing CQ nonlinear media. The parameters are chosen as, α3 = 1, α5 = − 0.00001, p = 1, m = 1, Θ = 0.15, b = 1.2, b10 = 2.1, c = 1, σ3 = σ5 = 21, δ3 = δ5 = 10, a Pc=262,890, Mc=650,000, b Pc=4,730,600, Mc=1,912,600

Full size image
Fig. 15
figure 15

Intensity distributions of the SELG solitons for propagation time t = 0 (black lines) and t = 3T (green lines). The parameters are all chosen as Fig. 14

Full size image

The formation powers of the (1, 1)- and (2, 2)-mode bistable SELG solitons in nonlocal competing self-focusing cubic and self-defocusing quintic nonlinear media versus degree of nonlocality, are shown as red and blue lines, respectively, in Fig. 16. One can see that, when the degree of nonlocality increases, the formation powers of the upper branch will decrease, whereas the lower branch will increase.

Fig. 16
figure 16

The critical powers (a) and OAMs (b) of bistable SELG solitons versus the degree of nonlocality in nonlocal competing CQ nonlinear media. The parameters are chosen as α3 = 1, α5 = − 0.00001, p = 1, m = 1, b = 1.2, c = 1 for red lines, α3 = 1, α5 = − 0.00001, p = 2, m = 2, b = 1.1, c = 1 for blue lines and α3 = 1, α5 = − 0.00002, p = 1, m = 1, b = 1.2, c = 1 for purple lines

Full size image

The solution of bistable solitons has a threshold of the degree of nonlocality. The upper and lower branches cross each other at the point of threshold. Above the threshold, solitons do not exist. The threshold will decrease when quintic nonlinear coefficient α2 increases. For example, the threshold is δ3 = δ5 = 12.4 for α5 = − 0.00001 (red lines) and δ3 = δ5 = 10.5 for α5 = − 0.00002 (purple lines).

4 Summary

In conclusion, the propagation of SELG soliton in nonlocal competing CQ nonlinear media was numerically studied. For convenience, the different-order SELG solitons with the same ellipticity were investigated first in nonlocal cubic nonlinear media (α3 = 1 and α5 = 0) and found that they have the same rotation period, cross-term phase coefficient, critical power and different critical OAMs. However, the stability of SELG soliton decreases as the order increases. Such that the completely stable (1, 5)- and (2, 4)-order SELG solitons cannot be formed. Second, we study the SELG solitons with different ellipticity in nonlocal quintic nonlinear media (α3 = 0 and α5 = 1) and the results show that the rotation period, cross-term phase coefficient, critical power and OAM are all increased as the ellipticity increases. In nonlocal competing nonlinear media, when α3 > 0 and α5 > 0, the completely stable SELG solitons also can be formed, but the critical power and OAM varies with the change of nonlinear coefficient and degree of nonlocality. For the case of α3 > 0 and α5 < 0, due to the competing self-focusing cubic and self-defocusing quintic nonlinearities, there are stable bistable SELG solitons, which have the same beam width and rotation period, but carrying larger or smaller powers as well as OAMs, in this media.