1 Introduction

Spatial NL phenomena resulting from the propagation of an intense laser beam in a Kerr medium have been widely studied for many years. Among others, we can cite studies involving self-focusing effects, soliton formation, or filamentation [1, 2]. The latter occurs when the laser peak power is greater than the so-called critical power Pcrit. The NL refractive index (n2), and the NL absorption coefficient, resulting from multiphoton absorption, are key parameters in these processes, as they govern most of NL optical third-order effect. Therefore, their measurement is of a prime importance. Beside the study of spatial NL phenomena, the NL optical characterization of materials is thus also giving rise to a lot of attention from the scientific community for decades. In that way, numerous bulk, liquid and gas materials have been characterized, mostly using the well-known Z-scan techniques [3, 4]. Nevertheless, we can cite other methods based on Kerr effect [5, 6], on supercontinuum generation [7], or on interferometric measurements [8]. Numerous applications covering many fields have emerged from these studies. In particular, applications in laser systems [9] or telecommunications [10] have been reported. The alteration of materials arising from such propagation has also been considered, with, for example, applications in medical surgery [11] or in underwater laser ablation [12]. Since a decade, colloids and quantum dot structures have also shown their potential for efficient observations of spatial NL effects [13, 14]. These structures are made of nanomaterials, mostly semiconductors, which are suspended in a solvent [15]. As a consequence, it has been shown that the magnitude and the sign of the overall nonlinearities of such structures can be fully controlled by the semiconductors of which they are composed. The size, the concentration and the shape of the quantum dots as well as the solvent used also influence the nonlinearities [16]. This behavior allows to engineer the structures for the generation of quasi on-demand NL properties [17, 18]. Functionalization of these structures could thus be envisioned. Very recently, the NL propagation of more exotic beams has been theoretically considered, including azimuthons and necklace beams [19], as they could enable parallel all-optical guiding [20].

Having relatively low NL coefficients, water, ethanol and tetrahydrofuran (THF) are among the most used liquids for solution or colloidal preparations. Their nonlinearities have been fully characterized in the visible and infrared (IR) domains [21,22,23,24]. However, studies reporting their characterization in the ultraviolet (UV) domain are very scarce. To the best of our knowledge, their characterization has been investigated only around 400 nm and for water only [7]. The Kerr effect in solvent that complicates correct estimation of third-order nonlinearities of solutes has not been sufficiently emphasized in the literature [25]. Moreover, the correct NL characterization of the solvent should take into account the response of the silica composing the cell. So, the main motivation for the present work is to fully characterize water, ethanol and THF solvents alone in the UV domain at 355 nm. We measure the NL refractive indices using the D4σ method [4, 26, 27] and the NL absorption coefficients are determined using the usual open-aperture Z-scan technique [3]. Combining both latter methods allows precise NL measurements of the third-order NL response. The experiments were made with laser intensities varying up to 150 GW/cm2. Finally, the critical power, above which filamentation occurs, is given. This parameter is of a great importance for the development of applications as well as for more fundamental studies.

This paper is organized as follows: in Sect. 2 a description of the experimental setup, the theory behind and the related numerical simulation are recalled briefly. The results of the NL refractive index and NL absorption measurements, at different laser intensities, are given in Sect. 3. A summary of the results and a conclusion complete this study.

2 Experiments

The measurements were made using a 10 Hz repetition rate Nd:YAG laser delivering 10-ps pulses (full width at half maximum) at 355 nm.

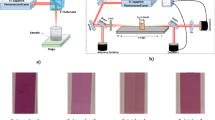
The experimental setup used to implement the D4σ-Z-scan technique is similar to that used in [4, 21] and shown in Fig. 1. The sample (NLM), composed of a 2.46-mm-thick quartz cell’s walls filled with either 2 mm liquid water, ethanol or THF, was mounted on a translation stage and moved along the beam propagation direction (z-axis) in the focus region. The overall process was automatized such that at each step of the motor (1 mm) an image of the output pulse, transmitted by the sample, was acquired by a CCD camera. A second arm was used to monitor the energy fluctuation of the incident laser pulses (via lens L3). The 4f imaging system composed of lenses L1 and L2 can be described with Fourier optics [26, 28]. Moving the sample in the focal region allows determination of the material’s NL parameters because the self-diffraction of the beam on the induced NL phase-shift and/or NL absorption at relatively high intensity originates changes in the transmitted image profile. The evolution of the beam waist relative variation (BWRV), estimated using the first and second moment of the recorded spatial beam intensity distribution, is then calculated versus the position z of the sample. The optical imaging system is aligned carefully to obtain a magnification equal to 1. Thus, it is possible to characterize accurately the profile of the beam (the object) at the entry in the linear regime, which is an important parameter. By means of the optical transfer function related to the free-space propagation over a finite distance and considering the phase transformations due to the lenses of 4f-system [29], we simulated the propagation of the beam from the object to the image plane considering the transmittance of the NL medium positioned at each motor step used for the Z-scan measurement. The transmittance of the NL medium was determined according to the evolution equations of NL phase-shift and intensity in the thin sample approximation [3]. Moreover, in what follows, nonlinear effects of order higher than three are neglected, and stimulated scatterings (Brillouin, Raman, and Rayleigh) are not taken into account. These approximations turn out to be valid because the exciting laser intensity remains below a limit value (the corresponding threshold value). Thermal effects are not significant when one is using ultrashort pulses in the picosecond range at low repetition rate [3]. The amplitude transmittance of the sample is described by \(T(z,u,v)={[1+q(z,u,v)]^{ - 1/2}}\exp [j\Delta \varphi _{{{\text{NL}}}}^{{{\text{eff}}}}\left( {z,u,v} \right)],\) where z stands for the position of the sample in the focus region. u = x/λf1 and v = y/λf1 are the normalized spatial frequencies with λ being the incident laser wavelength. \(q(z,u,v)={C_2}LI(z,u,v)\), where L denotes the thickness of the sample, I(z, u, v) is the intensity of the laser beam inside the sample and C2 in m/W is the two-photon NL absorption coefficient. The NL phase-shift is determined by \(\Delta \varphi _{{{\text{NL}}}}^{{{\text{eff}}}}(z,u,v)=2\pi {n_2}L{I_{{\text{eff}}}}(z,u,v)/\lambda\). The effective intensity seen by the sample is given by \({I_{{\text{eff}}}}(z,u,v)=I(z,u,v)\log [1+q(z,u,v)]/q(z,u,v)\). The peak on-axis NL phase-shift at the focus is \(\Delta {\varphi _0}=\Delta \varphi _{{{\text{NL}}}}^{{{\text{eff}}}}(0,0,0)\) (for more details see [4]). Finally, the fits of the Z-scan profiles provide the NL absorption (in a first step) and NL refraction (in a second step) coefficients of the medium by comparing numerical and experimental data. For each measurement, two sets of acquisitions were performed. The first set was performed in the NL regime and the second one in the linear regime. The linear regime is necessary to remove diffraction, diffusion and/or imperfection contributions from the NL results, due to sample inhomogeneities. Moreover, an image of the entry plane of the 4f-system is performed. This allows the use of the real input object distribution in the numerical simulations leading to high-accuracy NL characterization. To ensure a reliable definition of a noise-free object, we considered a circular aperture as in [30] and measured a radius about 1 mm. The main source of uncertainty comes from the absolute measurement of the laser pulse energy; the accuracy of the Joulemeter is about 10%. All measurements were performed at room temperature with linearly polarized light.

Fig. 1
figure 1

Experimental D4σ-Z-scan setup. The sample is scanned along the beam direction around the focal plane (z = 0). The labels refer to lenses (L1, L2 and L3 with f1 = 20 cm, f2 = 20 cm and f3 = 30 cm), beam splitters (BS1 and BS2), mirrors (M1 and M2) and nonlinear material (NLM)

Full size image

3 Results and discussion

To consider the contributions of the cell’s walls and the solvent, the total NL phase-shift is written as \(\Delta {\varphi _{\text{0}}}=\Delta {\varphi _{\text{c}}}+\Delta {\varphi _{\text{s}}}\), where the subscript c stands for cell and s for the solvent. This leads to the effective NL refractive index of the solvent:

$${\text{1.}}\;\;{\text{without}}\;{\text{NL}}\;{\text{absorption:}}\;\;{n_{2{\text{s}}}}=\frac{{\left( {\lambda \Delta {\varphi _0}/2\pi {I_0}} \right) - {n_{2{\text{c}}}}{L_{\text{c}}}}}{{{L_{\text{s}}}}}{,}$$
(1)
$${\text{2.}}\;\;{\text{with}}\;{\text{NL}}\;{\text{absorption:}}\;\;{n_{2{\text{s}}}}=\frac{{\left[ {\left( {\lambda \Delta {\varphi _0}/2\pi {I_0}} \right) - {n_{2{\text{c}}}}{L_{\text{c}}}} \right]{q_0}}}{{{L_{\text{s}}}\log (1+{q_0})}}{,}$$
(2)

where I0 is the peak focal on-axis intensity, Ls = 2 mm is the solvent thickness, Lc = 2.46 mm is the total thickness of the cell’s walls and q0 = C2I0Ls. The thin sample approximation is used. So, the total thickness of the cell (4.46 mm) should be small enough that changes in the beam diameter along this propagation distance due to either diffraction or NL refraction can be neglected [3].

Figure 2a shows an example of the BWRV versus z for the empty cell with I0 = 198 GW/cm2. The circles are the data and the solid line is the fit, giving n2c = (0.6 ± 0.1) × 10−20 m2/W. This is in agreement, taking into account experimental uncertainties, with previous work performed with similar quartz cells at different wavelengths [31], for which it was found n2c = (0.44 ± 0.1) × 10− 20 m2/W at 532 nm and n2c = (0.81 ± 0.16) × 10−20 m2/W at 1064 nm. This result confirms the nearly constant and very low NL refractive index of quartz from UV to near-IR. Figure 2b shows the variation of the NL refractive index with intensity from 39 to 198 GW/cm2. The error bars are calculated automatically by the program for each set of acquisitions. In addition to the classical error related to the Joulemeter, we take into account other errors depending on the optical quality of the material and on the fluctuations of the laser energy during the scan. These errors are estimated statistically for each scan in the linear regime where the specimen is far from the focus at the level of the signal wing profile (z ≈ ± 30 mm) where normally the BWRV should be equal to zero. Considering the measurement uncertainties in Fig. 2b, n2 remains constant for intensities up to 198 GW/cm2, the evolution is relatively stable, giving a mean value around (0.6 ± 0.2) × 10−20 m2/W. This indicates that the high-order nonlinearities of quartz are negligible in the UV domain.

Fig. 2
figure 2

a Beam waist relative variation versus z at I0 = 198 GW/cm2 using the empty cell (2.46 mm thick) at 355 nm (filled circle: data; solid line: fitting); b corresponding variation of the NL refractive index with intensity (empty cell)

Full size image

NL absorption was investigated for the cell alone in quartz and the three solvents. For the cell, water and ethanol, the NL absorption coefficients are found to be negligible (C2 < 0.01 × 10−11 m/W). However, for THF, as represented in Fig. 3, the NL absorption cannot be ignored. The absence of NL absorption in the cell alone allows to consider that the obtained C2 coefficient is only due to THF. For intensity up to 150 GW/cm2, two-photon absorption remains constant with a mean value C2 = (0.04 ± 0.01) × 10−11 m/W.

Fig. 3
figure 3

Variation of the two-photon absorption coefficient with intensity for THF at 355 nm

Full size image

The Kerr nonlinearities of the solvents were then characterized. First, the quartz cell was filled with water. The results are presented in Fig. 4. Considering both contributions due to the cell’s walls and the water, the overall NL refractive index remains constant, n2tot= (2.3 ± 0.8) × 10−20 m2/W (see Fig. 4b). As NL absorption of water is negligible, following Eq. (1), the NL refractive index of water alone is almost constant, n2w= (1.3 ± 0.2) × 10−20 m2/W for I0 below 200 GW/cm2. This value is in good agreement with a previous study realized at a wavelength of 407 nm [7]. More interestingly, the constant value of the NL refractive index with respect to the laser intensity reveals that no higher order optical nonlinearities are present for water under UV irradiation up to 200 GW/cm2. Finally, as expected, this value is slightly higher than the ones found at 532 nm [n2w = (0.96 ± 0.24) × 10−20 m2/W] and 1064 nm [n2w= (0.8 ± 0.2) × 10−20 m2/W] [21]. The comparison in the IR is done at intensities higher than 4 × 1015 W/m2 where the signal to noise ratio (S/N) is sufficient to ensure reliable effective n2 values in Fig. 4 of reference [21]. In this previous study, the poor S/N at lower intensities in Fig. 4 tilted to 0 the regression line fitting the fifth-order response of water making the n2 value very low. Currently and with the improvements in the image processing program to remove the noise of the CCD, considering only pixels whose gray-level values are higher than 10% of the maximum in the acquired images, the results are more reliable. Note that the water NL refractive index decreases with increasing the wavelength showing a behavior similar to the normal dispersion which occurs when the linear refraction index decreases with increasing the wavelength.

Fig. 4
figure 4

a Beam waist relative variation versus z at I0 = 105 GW/cm2 using the 2.46-mm-thick quartz cell’s walls filled with 2 mm water at 355 nm (filled circle: data; solid line: fitting); b corresponding variation of the NL refractive index with intensity

Full size image

The same experimental procedure is then followed for ethanol and THF. Figure 5 summarizes the results. The obtained values remain constant in the interval between 20 and 150 GW/cm2. Considering both contributions due to the cell’s walls and the material, the total NL refractive index is n2= (2.5 ± 0.6) × 10−20 m2/W for ethanol and n2= (3.0 ± 0.7) × 10−20 m2/W for THF. According to Eq. (1), the NL refractive index is n2e= (1.7 ± 0.3) × 10−20 m2/W for pure ethanol which is ten times lower than the one found in infrared (n2e = 18 × 10−20 m2/W at 1064 nm) [22]. However, in [22] the measurements were performed with respect to a calibration based on CS2 considering the n2 value given by [3]. Here the measurements are done without any calibration to a reference material but following the absolute intensity measurement in the focus region as described in [31]. As previously reported in [31], following this procedure for the characterization of CS2 leads to a 7.5 times lower NL refractive index value than that of the one reported in [3]. If we consider, in addition, that in the previous study of ethanol performed in IR domain [22], the NL response of the cell’s walls was not accounted, this explains the difference of one order of magnitude between the NL refractive indices in the UV and IR domains.

Fig. 5
figure 5

Variation of the NL refractive index at 355 nm with intensity for a 2.46-mm-thick quartz cell’s walls filled with a 2 mm of ethanol and b with 2 mm of THF

Full size image

The results obtained for THF and represented in Fig. 5b should be analyzed taking into account the influence of the NL absorption. Then, following Eq. (2) we found n2T = (2.1 ± 0.7) × 10−20 m2/W, which is almost the same value as the one obtained at 820 nm in the femtosecond regime (n2T = 2.3 × 10−20 m2/W) [23].

Finally, the critical power, \({P_{{\text{crit}}}}=3.77{\lambda ^2}/8\pi {n_0}{n_2}\) [32], above which filamentation in the material occurs, is given, as this parameter is of a great importance for numerous studies and potential applications. n0 is the linear refractive index. Taking into account the chromatic dispersion of n0 with the laser wavelength, we obtain Pcrit = 0.66 MW for water at 355 nm. This value is in a good agreement with a previous study [24], performed at a wavelength of 407 nm with subpicosecond pulses. Corresponding critical powers for ethanol and THF are Pcrit = 0.49 MW and Pcrit = 0.39 MW, respectively. All the results are summarized in Table 1.

Table 1 NL coefficients measured at 355 nm for water, ethanol and THF
Full size table

4 Conclusion

In the present paper, we have reported on the NL characterization of water, ethanol and THF under UV high irradiance at 355 nm in the picosecond regime. For the three solvents, considered in this study, the NL refractive indices remain constant [n2w = (1.3 ± 0.2) × 10−20 m2/W for water, n2e = (1.7 ± 0.3) × 10−20 m2/W for ethanol and n2T = (2.1 ± 0.7) × 10−20 m2/W for THF] for intensities up to 150 GW/cm2. Therefore, no higher order optical nonlinearities are present in the UV domain up to this available power. NL absorption coefficients have also been investigated. They are found to be negligible for water and ethanol, and low for THF (C2 = 0.04 ± 0.01 cm/GW). Finally, the critical power remains below 1 MW for the three solvents. We expect the present study to be useful for numerous future fundamental interest or potential applications in the UV domain.