1 Introduction

The development of ultrashort high-power lasers in the last decade has opened new and active research fields such as fast ignition of inertial confinement fusion (ICF) [1,2,3], high-order-harmonic generation (HHG) [4,5,6], X-ray generation [7], laboratory astrophysics [8, 9], and development of a compact source of high-energy electrons and ions [10,11,12,13]. Copious amounts of experimental investigations have demonstrated the collimated pulses of energetic ions produced in the interactions of short intense laser pulses with solid density thin foil targets [14,15,16,17]. Due to the wide range of potential applications, from high-resolution radiography imaging, probing for the strong electrostatic fields induced in plasmas, radioisotope production, and isochoric heating, to cancer therapy [18], the generation of mono-energetic ion pulses has been an attractive area for researchers recently.

In most of aforementioned applications, there is an interaction of a laser field with overdense plasma. For example, in the target normal sheath acceleration (TNSA), the interaction between a high-intensity (\(10^{18}-10^{21}\,{\text {W/cm}}^2\)) laser pulse with foil targets ranging in thickness from a few to several tens of microns leads to the emission of multi-MeV, high-quality ion pulses [19]. Making use of the relatively new mechanism called radiation pressure acceleration (RPA), particles gain energy directly from the radiation pressure exerted on the target by the laser pulse [20,21,22,23,24,25,26,27,28]. This mechanism has been proposed as a method to get high quality and much more efficient ion beams in comparison with TNSA. To achieve and dominate acceleration for RPA mechanism, a thin foil is irradiated by a circularly polarized laser pulse at normal incidence. For the RPA mechanism electron heating is strongly suppressed to transfer the laser energy directly for ion acceleration. On the other hand, in ICF scenario, a picosecond relativistic laser is required to transmit its energy through large inhomogeneous plasma for rapidly heating of the compressed fuel core in nuclear fusion ignition. To achieve energy gain, the laser energy should be more than 1 MJ within a few nanoseconds. Therefore, in contrast to the RPA mechanism, a strong absorption of laser energy by electrons is required to achieve an efficient ICF process. On the other hand, different numerical and experimental investigations revealed that the laser pulse can be focused during propagation through overdense plasma [29, 30]. Self-focusing of the laser pulse reduces the pulse spot size and enhances laser intensity by more than 1 order of magnitude while temporally steepening the Gaussian pulse and improving the laser contrast [31,32,33,34,35,36,37,38]. When electrons are accelerated, up to the relativistic velocity, inside a self-focused laser pulse, electric currents, and an associated quasi-static magnetic field are produced in plasma. It has been shown that the strength of the axial part of the self-generated magnetic field in the laser interaction with underdense plasma is around a few MG [39]; however, saturation strength can reach up to 107.1 MG in overdense plasmas [31]. It is clear that generation of the magnetic field is a non-linear phenomenon and the magnetic field can be induced in the relativistic laser–plasma interaction. In the present paper, the magnetic field is produced by IFE mechanism in the interaction between a circularly polarized laser field with plasma[40].

In the course of this paper, we consider an overdense axially magnetized plasma lens under normal irradiation of a high-intensity right or left circularly polarized pulse with the normalized vector potential \(a_{00}={\text {eE}}_{00}/m_e\omega c>1\). Overdense plasma can be produced by the interaction of a high-intensity circularly polarized pulse with a thin foil target and the axial magnetic field is modeled as a self-generated magnetic field owing to this interaction. Here, we will use an ultrathin lens due to the present possibility of manufacturing of diamond-like carbon and or polymer-based ultra-thin (sub 10 nm) foil targets [41, 42]. The Fresnel’s coefficients for the right- and left-handed circularly polarized laser pulses propagating through overdense plasma with electron density \(n_e=10n_c\) are obtained by the numerical solution of the coupled differential equations for relativistic factor \(\gamma\) and wave propagation. We find that in the absence of the axial magnetic field and ponderomotive force, opaque plasma becomes transparent and relativistic self-focusing (RSF) takes place. The required normalized vector potential for the RSF is around \(a_{00}\approx 2.5\). It is important to note that, in the laser-plasma interaction in the relativistic regime \(a_{00}>1\), both the self-generated magnetic field and ponderomotive force exist in a real physical system. Therefore, we would like to consider their influences in the course of this paper.

The results revealed that the transmission of a left-handed circularly polarized pulse through the overdense plasma lens is facilitated by increasing the strength of the magnetic field; however, for a right-handed circularly polarized pulse, the transmission is decreased for the laser pulse with vector potential smaller than that required for RSF. Based on the numerical solution, the magnetic field enhances self-focusing effect for the right and weakens it for the left-handed pulses. When the influence of ponderomotive force is taken into account, the critical power for self-focusing of both polarizations is decreased and the Fresnel’s coefficients are changed.

We begin Sect. 2 by a brief review about the anomalous tunneling of the right and left circularly polarized laser pulses through overdense magnetized plasma. In this section, the wave equation for the laser field inside the magnetized plasma lens is obtained. It is shown that the wave equation is coupled with a differential equation in terms of the relativistic factor \(\gamma\). In Sect. 3 we will solve the wave equation and a differential equation for \(\gamma\) as a system of equations by making use of Runge–Kutta technique with proper boundary conditions and the influence of the ponderomotive force is considered and it is shown how the results are modified. Our results are summarized in Sect. 4.

2 Fresnel coefficients and anomalous tunneling

Let us consider a plasma lens with thickness \(\varDelta\) irradiated normally by a circularly polarized pulse from the \(z<0\) side. Here, we assume that the plasma lens is located on \(0<z<\varDelta\). The electric and magnetic fields of a Gaussian circularly polarized laser pulse are given by

$$\begin{aligned} (E_i,B_i)=(\hat{e}_{r\pm },\mp i\hat{e}_{r_\pm })E_0 e^{-i(\omega t-\frac{\omega }{c}z)}, \end{aligned}$$
(1)

where \(\hat{e}_{r_{\pm }}=\hat{e}_{x} \pm i\hat{e}_{y}\) and the subscripts ± refer to the right (+) and left (−) circularly polarized laser pulses, respectively. Moreover, \(E_0\) and \(\omega\) are laser field amplitude and frequency, respectively. For a Gaussian pulse, we consider \(E_0^2=E_{00}^2 e^{-r^2/r_0^2}\), where \(r_0\) defines the initial pulse radius at \(z=0\). Under the condition \(r^2\ll r_0^2\) which is satisfied as well inside the plasma lens, we can divide the cross section of the laser pulse into small parts and consider each part as a plane wave inside the plasma lens. To do this, we introduce the incident, reflected, and transmitted waves as

$$\begin{aligned} (E_{1i},B_{1i})= & {} (\hat{e}_{r\pm },\mp i\hat{e}_{r_\pm })E_{1} e^{-i(\omega t-\frac{\omega }{c}z)},\nonumber \\ (E_{1r},B_{1r})= & {} (\hat{e}_{r\pm },\pm i\hat{e}_{r_\pm })RE_{1} e^{-i(\omega t+\frac{\omega }{c}z)},\nonumber \\ (E_{1t},B_{1t})= & {} (\hat{e}_{r\pm },\mp i\hat{e}_{r_\pm })E_{3} e^{-i(\omega t-\frac{\omega }{c}z)}, \end{aligned}$$
(2)

where \(E_1\) and \(E_3\) are incident and transmitted wave amplitude and R is the reflection coefficient, respectively. If we assume the electric field of the laser pulse as \(E_2=\hat{e}_{r\pm }p(z)e^{-i\omega t}\), the wave equation governed by the envelope of p(z) is

$$\begin{aligned} \frac{{\text {d}}^2\bar{p}(z)}{{\text {d}}z^2}+\frac{\omega ^2}{c^2}\epsilon _{\pm } \bar{p}(z)=0, \end{aligned}$$
(3)

where \(\epsilon _{\pm }=1-\omega _p^2/\omega (\omega \mp \omega _c/\gamma )\gamma\) defines the plasma dielectric permittivity, \(\omega _c=eB/m_0c\) and \(\omega _p=(4\pi ne^2/m_0)^{1/2}\) are non-relativistic Larmor and plasma frequencies and \(-e\) and \(m_0\) are electron charge and rest mass, respectively. Furthermore, \(\bar{p}(z)=eE_2/m_0\omega c\) is normalized laser pulse amplitude (or normalized vector potential). The relativistic factor \(\gamma\) can be written as [43]

$$\begin{aligned} \gamma =\left( 1+\frac{\bar{p}(z)^2}{\left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^2}\right) ^{1/2}. \end{aligned}$$
(4)

Here, the upper and lower signs in all equations correspond to the right- and left-handed circularly polarized pulses. It should be noted that we have neglected the charge density variation and we will proceed it later when the influence of the ponderomotive force is included. To hold the boundary conditions on the back and front sides of the lens, we need to consider the magnetic field inside plasma which is given by \(B_2=(\mp \hat{e}_{r\pm })\frac{c}{\omega } \frac{{\text {d}}p(z)}{{\text {d}}z}e^{-i\omega t}\). The continuity for tangential components of the electric and magnetic fields at \(z=\varDelta\) yields

$$\begin{aligned} \bar{p}(\varDelta )= & {} \bar{E}_3e^{i(\frac{\omega }{c})\varDelta },\nonumber \\ \frac{{\text {d}}\bar{p}}{{\text {d}}z}|_{(z=\varDelta )}= & {} i\frac{\omega }{c}\bar{E}_3e^{i(\frac{\omega }{c})\varDelta }, \end{aligned}$$
(5)

where \(\bar{E}_3\) refers to normalized laser pulse amplitude \(\bar{E}_3=eE_3/m_0\omega c\). Similarly, by employing the continuity of the fields at \(z=0\), we arrive

$$\begin{aligned} (1+R)E_1= & {} p(0),\nonumber \\ (1-R)E_1= & {} -i\frac{c}{\omega }\frac{{\text {d}}p}{{\text {d}}z}|_{(z=0)}. \end{aligned}$$
(6)

Now, from Eq. (6), we can obtain

$$\begin{aligned} \bar{E}_1= & {} \frac{1}{2}\left( \bar{p}(0)-i\frac{c}{\omega }\frac{{\text {d}}\bar{p}}{{\text {d}}z}|_{(z=0)}\right) ,\nonumber \\ R= & {} \frac{\left( \bar{p}(0)+i\frac{c}{\omega }\frac{{\text {d}}\bar{p}}{{\text {d}}z}|_{(z=0)}\right) }{\left( \bar{p}(0)-i\frac{c}{\omega }\frac{{\text {d}}\bar{p}}{{\text {d}}z}|_{(z=0)}\right) }. \end{aligned}$$
(7)

Obviously, \(E_1\) is a complex variable and it is written in the form \(E_1=|E_1|e^{i\varPhi }\). Therefore, writing \(p=p_r+ip_i\), we arrive

$$\begin{aligned} \varPhi =\tan ^{-1}\left( \frac{\bar{p}_i(0)-\frac{c}{\omega }\frac{{\text {d}}\bar{p}_r}{{\text {d}}z}|_{(z=0)}}{\bar{p}_r(0)+\frac{c}{\omega }\frac{{\text {d}}\bar{p}_i}{{\text {d}}z}|_{(z=0)}}\right) . \end{aligned}$$
(8)

It is clear that \(E_1\) will be real if we assume a phase factor \(e^{-i\varPhi }\) for \(E_3\). This means that the phase change \(-\varPhi\) is imposed on the laser pulse during propagation through the plasma lens. Note that we divided the Gaussian pulse to the small beamlets (plane waves); therefore, the different beamlets will suffer different phase shifts. If we assume that the central spot (\(r=0\)) suffers the phase shift \(\varPhi _0\), for a beamlet at r (\(r\ll r_0\)) the phase shift is given by

$$\begin{aligned} \varPhi= & {} \varPhi _0+\frac{\partial \varPhi }{\partial E_{00}}(E_{00}-E_{00} e^{-r^2/2r_0^2}),\nonumber \\\approx & {} \varPhi _0+\frac{\partial \varPhi }{\partial E_{00}}E_{00}\frac{r^2}{2r_0^2}. \end{aligned}$$
(9)

According to the phase constancy of the wavefront of a plane wave (i.e., \(\omega z/c-\varPhi\) = constant), the wavefront converges to the radius of curvature:

$$\begin{aligned} R_c=\left| \frac{\partial ^2z}{\partial r^2}\right| ^{-1}=\frac{\omega }{c}r_0^2\frac{1}{\left| \frac{\partial \varPhi }{\partial E_{00}}E_{00}\right| }. \end{aligned}$$
(10)

To have a complete set of equations we differentiate Eq. (4) with respect to z. Therefore, we find

$$\begin{aligned} \left( \gamma \pm \frac{\omega _c\bar{p}(z)^2}{\omega \gamma ^2\left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^3}\right) \frac{{\text {d}}\gamma }{{\text {d}}z}= \frac{\bar{p}(z)\frac{{\text {d}}\bar{p}(z)}{{\text {d}}z}}{\left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^2}. \end{aligned}$$
(11)

3 Method of solution

3.1 In the absence of ponderomotive force

In this section, we are going to solve the set of Eqs. (3) and (11), by making use of the proper boundary conditions. To do this, first, we pick up an arbitrary value for \(\bar{E}_3\) and solve Eq. (4) at \(z=\varDelta\) for a given parameter \(\omega _c/\omega\). We choose the parameters \(\omega \varDelta /c=0.5\) and \(\omega _p^2/\omega ^2=10\). Therefore, the values of \(\bar{p}(\varDelta )\) and \(\frac{{\text {d}}\bar{p}}{{\text {d}}z}|_{(z=\varDelta )}\) are known. Next, we proceed backward, solving the set of Eqs. (3) and (11) using Runge–Kutta technique. After solving the equations, the amplitude of laser pulse is determined at \(z=0\). Thus, using Eq. (7), the transmission (i.e., \(T=|\bar{E}_3/\bar{E}_1|\)) and reflection coefficients are obtained. It is important to note that in this method, we do not use of any approximation to evaluate the parameter \(\gamma\), which is widely used in the previous studies [44], but in contrast, this value is obtained directly by numerical solution of Eq. (4). In this method, we should solve wave equation (3) and the first-order differential equation for \(\gamma\) together as a system of equations.

Fig. 1
figure 1

Transmission coefficients correspond to the right (red line)- and left (green line)-handed pulses transmitted through a magnetized plasma lens for \(\omega _c/\omega =0.4\), as a function of \(a_{00}\). Point line shows transmission coefficient corresponds to a laser pulse transmitted through an unmagnetized plasma lens as a function of \(a_{00}\)

Full size image

Figure 1 depicts the variation of the laser transmission coefficient as a function of normalized laser pulse amplitude. The red and green solid lines correspond to the right- and left-handed pulses and the point line regards to the propagation of a circularly polarized pulse through a non-magnetized plasma lens, respectively. The figure shows that the left-handed pulse is more effectively transmitted through magnetized overdense plasma compared to the right-handed one. Furthermore, the transmission coefficients for both polarizations increase with \(a_{00}\) as the effective plasma frequency \(\omega _{eff}=\omega _p/\gamma ^{1/2}\) decreases. We know the plasma refractive index is \(n_{\pm }=\sqrt{\epsilon _{\pm }}=\sqrt{1-\omega _p^2/\omega (\omega \mp \omega _c/\gamma )\gamma }\), where the upper and lower signs refer to the right- and left-handed pulses. Therefore, the plasma refractive index can be varied by plasma density, magnetic field strength, and relativistic effect. Therefore, we expect the transmission of left- and right-handed pulses to be different, because they have different refractive index in the presence of the magnetic field. On the hand, it is important to note that the relativistic factor \(\gamma\) is strongly coupled with the magnetic field by Eq. (4), and therefore, the clear explanation about how the refractive index for right- and left-handed laser pulse can be changed by the magnetic field is impossible. This means that, we unable to explain the propagation of the right- and left-handed pulses without numerical solution of Eq. (3).

Figure 2 plots the dependence of reflection coefficients of the right- and left-handed laser pulses as a function of \(a_{00}\). The perceptible difference between the right- and left-handed pulses is obvious in this figure. While reflection amplitude increases for the right-handed pulse by considering the self-generated magnetic field effect, reflection amplitude decreases for the left-handed pulse. Reflection amplitude decreases for both polarizations with increasing the laser pulse amplitude. From Figs. 1 and 2, one can see that the difference between two polarizations disappears for sufficiently intense laser pulse when the relativistic effect overcomes to the self-generated magnetic field influence.

Fig. 2
figure 2

Reflection coefficients correspond to the right (red line)- and left (green line)-handed pulses transmitted through a magnetized plasma lens as a function of \(a_{00}\) for \(\omega _c/\omega =0.4\). Point line shows reflection coefficient corresponds to a laser pulse transmitted through an unmagnetized plasma lens as a function of \(a_{00}\)

Full size image

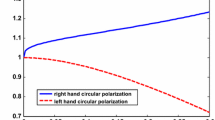
The variation of the normalized radius of curvature \(R_c/(\omega /c)r_0^2\) as a function of \(a_{00}\) is plotted in Fig. 3. This figure shows that the self-generated magnetic field enhances the self-focusing effect for the right-handed and weakens it for the left-handed pulses. It is found from Fig. 3 that the central portion of a right-handed pulse tunnels through the magnetized plasma lens more effectively compared to the left-handed pulse, while marginal rays suffer strong reflection. As a result, the output right-handed pulse has a smaller spot size in comparison with the left one.

The interaction of the high-intensity laser pulse with thin foils has been widely used to produce few-fs nearly single-cycle ultraintense light [45]. In this mechanism for suitably chosen laser and foil parameter, the foil is transparent only to the highest intensity part of the laser pulse. Therefore, the transmitted pulse has a much shorter than the incident pulse. This paper suggested that if we use a right-handed pulse in laser-foil interaction , it is possible to produce more intense, much shorter, and very small spot size output pulses. This effect arises due to the influence of self-generated magnetic field.

Fig. 3
figure 3

Normalized radius of curvature of transmitted wavefront as a function of \(a_{00}\) for the right (red line)- and left (green line)-handed pulses for \(\omega _c/\omega =0.4\). Point line shows the normalized radius of curvature of wavefront transmitted through an unmagnetized plasma lens as a function of \(a_{00}\)

Full size image

3.2 In the presence of ponderomotive force

Fig. 4
figure 4

Transmission coefficients correspond to the right (red line)- and left (green line)-handed pulses transmitted through a magnetized plasma lens as a function of \(a_{00}\) for \(\omega _c/\omega =0.4\), in the presence (solid lines) and in the absence (dashed-dotted lines) of the ponderomotive force

Full size image

It is obvious that an intense Gaussian short laser pulse can exert a ponderomotive force on electrons, due to the laser field nonuniform distribution. When electrons feel this force, they move away from the region of the maximum field amplitude. The longitudinal component of the electron fluid momentum is given as [46]

$$\begin{aligned} \frac{\partial {\mathbf{p}}_L}{\partial t}=e{\varvec{\nabla }} \phi -m_0c^2{\varvec{\nabla }}(\gamma -1), \end{aligned}$$
(12)
Fig. 5
figure 5

Reflection coefficients correspond to the right (red line)- and left (green line)-handed pulses transmitted through a magnetized plasma lens as a function of \(a_{00}\) for \(\omega _c/\omega =0.4\), in the presence (solid lines) and in the absence (dashed-dotted lines) of the ponderomotive force

Full size image

where the first term is the electrostatic force arises from the electron-ion separation and second term can refer to the relativistic ponderomotive force, from which the potential is found as \(U_p=m_0c^2(\gamma -1)\). Physically, for a laser pulse duration shorter than the ion plasma period, the ion is immobile. Therefore, the first term in Eq. (12) is of a charge imbalance between the electrons and ions. In the quasi-steady state, we expect that \(\phi =U_p\). Under this condition and making use of the Poission\(^,\)s equation \(\nabla ^2\phi =4\pi e(n_e-n_0)\), we arrive

$$\begin{aligned} n_e=n_0\left( 1-\frac{c^2}{\omega _p^2}\nabla ^2\gamma \right) . \end{aligned}$$
(13)

By employing the density profile equation (13) in Eq. (3), we will find the wave equation for the laser pulse inside the plasma lens:

$$\begin{aligned} \frac{{\text {d}}^2\bar{p}(z)}{{\text {d}}z^2}+\left[ \frac{\omega ^2}{c^2}\epsilon \left( 1-\frac{c^2}{\omega _p^2}\frac{{\text {d}}^2\gamma }{{\text {d}}z^2}\right) \right] \bar{p}(z)=0. \end{aligned}$$
(14)

In this stage, we need a second equation along with Eq. (14). Hence, differentiating Eq. (11), we obtain a second order differential equation for \(\gamma\):

$$\begin{aligned}&\frac{{\text {d}}^2\gamma }{{\text {d}}z^2}\left( \gamma \pm \frac{\bar{p}(z)^2\omega _c}{\gamma ^2\omega (1\mp \frac{\omega _c}{\gamma \omega })^3}\right) +\alpha \left( \frac{{\text {d}}\gamma }{{\text {d}}z}\right) ^2\pm \beta \frac{{\text {d}}\gamma }{dz}\nonumber \\&\quad =\frac{\left( \frac{{\text {d}}\bar{p}(z)}{{\text {d}}z}\right) ^2+\bar{p}(z)\frac{{\text {d}}^2\bar{p}(z)}{{\text {d}}z^2}}{\left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^2}, \end{aligned}$$
(15)

where \(\alpha\) and \(\beta\) are given as

$$\begin{aligned} \alpha= & {} \left( 1\mp \frac{2\bar{p}(z)^2\omega _c}{\gamma ^3\omega \left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^3}-\frac{3\bar{p}(z)^2\omega _c^2}{\gamma ^4\omega ^2\left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^4}\right) ,\nonumber \\ \beta= & {} \left( \frac{4\bar{p}(z)\frac{{\text {d}}\bar{p}(z)}{{\text {d}}z}\omega _c}{\gamma ^2\omega \left( 1\mp \frac{\omega _c}{\gamma \omega }\right) ^3}\right) . \end{aligned}$$
(16)

Now, we are able to solve the coupled differential equations (14) and (15) using Runge–Kutta technique. Note that the boundary conditions are the same as those used in subsection A; however, the boundary condition for \(\frac{{\text {d}}\gamma }{{\text {d}}z}|_{(z=\varDelta )}\) can be obtained from Eq. (11).

Fig. 6
figure 6

Normalized radius of curvature of transmitted wavefront as a function of \(a_{00}\) for the right (red line)- and left (green line)-handed pulses for \(\omega _c/\omega =0.4\), in the presence (solid lines) and in the absence (dashed-dotted lines) of the ponderomotive force

Full size image

Figure 4 shows the transmission coefficients for the right- and left-handed laser pulse as a function of \(a_{00}\). The solid and dashed lines are figured in the presence and absence of the ponderomotive force, respectively. The pulse transmission for both polarizations consists of an appreciable increase in the presence of the ponderomotive force. In other words, the ponderomotive force facilitates the pulse transmission through overdense plasma by making change of the electron density profile. The reflection coefficients for the laser pulse transmitted through plasma lens is displayed in Fig. 5 in terms of \(a_{00}\). Clearly, the reflection coefficients for both polarizations are decreased compared to the case when the influence of the ponderomotive force is ignored. Figure 6 displays the normalized radius of curvature for both polarizations in the presence and absence of the ponderomotive force. It is found from this figure that the intensity required for self-focusing is decreased when the influence of the ponderomotive force is included. For example, for the right- and left-handed pulses, the self-focusing takes place for \(a_{00}\approx 1.25\) and \(a_{00}\approx 1.5\) instead of \(a_{00}\approx 1.5\) and \(a_{00}\approx 3\), respectively. Moreover, this figure shows that the right-handed pulse is more effectively focused by the plasma lens in comparison with the left-handed one.

4 Summary and conclusion

In summary, we have studied laser pulse transmission through a magnetized overdense plasma lens. Overdense plasma can be produced in the laser pulse interaction with a ultrathin foil and the strong self-generated magnetic field was modeled as an external magnetic field. Here, a circularly polarized laser pulse was normally irradiated on the plasma target and propagated parallel to the external magnetic field. The influences of the self-transparency, ponderomotive force, and external magnetic field were considered in the right- and left-handed circularly polarized laser pulse transmission through overdense plasma. The numerical investigations revealed that in the absence of the ponderomotive force, the external magnetic field facilitated left-handed pulse transmission and weakened it for right-handed pulse. We have shown that the external magnetic field enhances the self focusing effect for the right and weakens it for the left-handed pulses. The inclusion of the ponderomotive force demonstrated the important role of this force in the laser pulse interaction with overdense plasma. In this case, the laser pulse transmission was sufficiently increased for both polarizations compared to the case when the ponderomotive force was missed. The results presented in this paper manifested that the ponderomotive force decreased the intensity required for laser pulse self-focusing for both polarizations. The difference between the right- and left-handed pulses lead us to use of them for different experimental applications. For example, we can produce much more intense pulses of very small spot size in the interaction of a right-handed pulse with a thin foil. Moreover, it seems ICF experiment can be very effective with a right-handed pulse.