Generation of a sub-half-wavelength focal spot with purely transverse spin angular momentum

Abstract

We theoretically demonstrate that optical focus fields with purely transverse spin angular momentum (SAM) can be obtained when a kind of special incident fields is focused by a high numerical aperture (NA) aplanatic lens (AL). When the incident pupil fields are refracted by an AL, two transverse Cartesian components of the electric fields at the exit pupil plane do not have the same order of sinusoidal or cosinoidal components, resulting in zero longitudinal SAMs of the focal fields. An incident field satisfying above conditions is then proposed. Using the Richard–Wolf vectorial diffraction theory, the energy density and SAM density distributions of the tightly focused beam are calculated and the results clearly validate the proposed theory. In addition, a sub-half-wavelength focal spot with purely transverse SAM can be achieved and a flattop energy density distribution parallel to z-axis can be observed around the maximum energy density point.

1 Introduction

Recently, light with transverse SAM has attracted more and more attention [1,2,3,4,5,6,7]. Optical fields with transverse SAM are likely playing an important role in many areas, such as high-resolution microscopy [8], optical trapping [9], particle manipulation [10] and so on. But transverse SAM can only be generated under certain conditions, including plasmonic, evanescent wave and strongly focused beams [17, 18]. An ordinary paraxial beam propagating in free space, which is generally considered as a transverse electric field, has no transverse SAM (In this paper, we only discuss electric fields instead of magnetic fields). With the help of a high NA AL, focused beams with purely transverse SAM have been realized by a particular paraxial beam focusing [6, 7]. However, the focal spot obtained in the literature [7] is not small enough, while a sub-half-wavelength focal spot is usually required in some applications [11, 12]. In this paper, we first theoretically demonstrate that optical focus fields with purely transverse SAM can be obtained when a kind of special incident pupil fields is focused by a high NA AL. Then we propose a concrete incident field that can be realized by spatial light modulators and binary optical elements [12,13,14]. And a sub-half-wavelength focal spot with purely transverse SAM is obtained.

2 Theory analysis

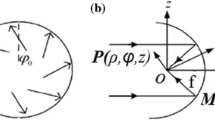
As shown in Fig. 1, using the Richard–Wolf vectorial diffraction method [15], the electric field near the focus can be expressed as:

Fig. 1

Focusing of a collimated beam with high NA AL. $\overrightarrow {{E_{i} }} (\theta ,\varphi )$ is the incident field.$\overrightarrow {{E_{o} }} (\theta ,\varphi )/\!\sin\theta$, to which a black arrow is pointed, is the field at the exit pupil plane. $\overrightarrow {E} (r,\phi ,z)$ is the field near the focal spot

$$\begin{aligned} \overrightarrow {E} (r,\phi ,z) &= \frac{1}{i\lambda }\int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{2\pi } {\sin \theta P(\theta ){\mathbf{A}}(\theta ,\varphi )\overrightarrow {{E_{i} }} (\theta ,\varphi )} } \hfill \\ &\quad \times\exp [ikz\cos \theta + ikr\sin \theta \cos (\varphi - \phi )]{\text{d}}\varphi {\text{d}}\theta , \hfill \\ \end{aligned}$$

(1)

where

$${\mathbf{A}}(\theta ,\varphi ) = \left[ {\begin{array}{*{20}l} {\cos ^{2} \varphi \cos \theta + \sin ^{2} \varphi } \hfill & {\sin \varphi \cos \varphi (\cos \theta - 1)} \hfill \\ {\sin \varphi \cos \varphi (\cos \theta - 1)} \hfill & {\sin ^{2} \varphi \cos \theta + \cos ^{2} \varphi } \hfill \\ {\sin \theta \cos \varphi } \hfill & {\sin \theta \sin \varphi } \hfill \\ \end{array} } \right],$$

(2)

$$\overrightarrow {{E_{i} }} (\theta ,\varphi ) = E_{1} (\theta ,\varphi )\overrightarrow {{e_{x} }} + E_{2} (\theta ,\varphi )\overrightarrow {{e_{y} }} .$$

(3)

In Eq. 1, λ is wavelength; θ _max is the maximum angle determined by the NA of the AL; P(θ) is the pupil plane apodization function, for the AL, P(θ) = cos^1/2 θ; A(θ, φ) is the polarization transformation matrix from an entrance pupil field to an exit pupil field; $\overrightarrow {{E_{i} }} (\theta ,\varphi )$ is the amplitude function of the incidence beam which does not own longitudinal components; k is wave number.

Assume that

$$\begin{aligned} &\overrightarrow {{E_{o} }} (\theta ,\varphi ) = \sin \theta P(\theta ){\mathbf{A}}(\theta ,\varphi )\overrightarrow {{E_{i} }} (\theta ,\varphi ) \hfill \\ &\quad = \left[ {\sum\nolimits_{m = 0}^{\infty } {e^{{i\varPhi_{1m} }} f_{1m} (\theta )\cos m\varphi )\; + \sum\nolimits_{m = 1}^{\infty } {e^{{i\varPsi_{1m} }} g_{1m} (\theta )\sin m\varphi )} } } \right]\overrightarrow {{e_{x} }} \hfill \\ &\qquad + \left[ {\sum\nolimits_{m = 0}^{\infty } {e^{{i\varPhi_{2m} }} f_{2m} (\theta )\cos m\varphi ) + \sum\nolimits_{m = 1}^{\infty } {e^{{i\varPsi_{2m} }} g_{2m} (\theta )\sin m\varphi )} } } \right]\;\overrightarrow {{e_{y} }} \hfill \\ &\qquad + \left[ {\sum\nolimits_{m = 0}^{\infty } {e^{{i\varPhi_{3m} }} f_{3m} (\theta )\cos m\varphi )} + \sum\nolimits_{m = 1}^{\infty } {e^{{i\varPsi_{3m} }} g_{3m} (\theta )\sin m\varphi )} } \right]\overrightarrow {{e_{z} }} , \hfill \\ \end{aligned}$$

(4)

where Φ _nm , Ψ _nm ∊ [0, π), f _nm (θ) and g _nm (θ) are unary real functions (n = 1, 2, 3). To be simpler, we use f _nm  = f _nm (θ), g _nm  = g _nm (θ) and∑ = ∑  ^∞ _m=0 . Substituting Eq. 4 into Eq. 1:

$$\begin{aligned} &\overrightarrow {E} (r,\phi ,z) = E_{x} \overrightarrow {{e_{x} }} + E_{y} \overrightarrow {{e_{y} }} + E_{z} \overrightarrow {{e_{z} }} \hfill \\ &\quad = ik\int_{0}^{{\theta_{\hbox{max} } }} {\bigg[\sum {i^{m} (e^{{i\varPhi_{1m} }} f_{1m} \cos m\phi + e^{{i\varPsi_{1m} }} g_{1m} \sin m\phi )J_{m} } \overrightarrow {{e_{x} }} } \hfill \\ &\qquad + \sum {i^{m} (e^{{i\varPhi_{2m} }} f_{2m} \cos m\phi + e^{{i\varPsi_{2m} }} g_{2m} \sin m\phi )J_{m} } \overrightarrow {{e_{y} }} \hfill \\ &\qquad + \sum {i^{m} (e^{{i\varPhi_{3m} }} f_{3m} \cos m\phi + e^{{i\varPsi_{3m} }} g_{3m} \sin m\phi )J_{m} } \overrightarrow {{e_{z} }} \bigg] \hfill \\ &\qquad \times \exp (ikz\cos \theta )d\theta , \hfill \\ \end{aligned}$$

(5)

SSSwhere J _m  = J _m (krsinθ), J _m (x) is the Bessel function of the first kind with order m. With Eq. 5, the SAM density can be calculated.

Since we only consider electric fields rather than magnetic fields, the SAM density can be written explicitly as [1, 16]:

$$\begin{aligned} &\overrightarrow {s} (r,\phi ,z) = s_{x} \overrightarrow {{e_{x} }} + s_{y} \overrightarrow {{e_{y} }} + s_{z} \overrightarrow {{e_{z} }} \hfill \\ &\quad\propto \text{Im} (E_{y}^{*} E_{z} )\overrightarrow {{e_{x} }} + \text{Im} (E_{z}^{*} E_{x} )\overrightarrow {{e_{y} }} + \text{Im} (E_{x}^{*} E_{y} )\overrightarrow {{e_{z} }} . \hfill \\ \end{aligned}$$

(6)

Meanwhile, the SAM per unit length (along z-axis) can be expressed as:

$$\overrightarrow {\zeta } (z) = \zeta_{x} \overrightarrow {{e_{x} }} + \zeta_{y} \overrightarrow {{e_{y} }} + \zeta_{z} \overrightarrow {{e_{z} }} = \int_{0}^{\infty } {\int_{0}^{2\pi } {\overrightarrow {s} (r,\phi ,z){\text{d}}\phi r{\text{d}}r} } .$$

(7)

Substituting Eqs. 5 and 6 into Eq. 7, the SAM per unit length can be expressed as:

$$\begin{aligned} &\zeta_{x} (z) \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{\infty } } } \hfill \\ &\bigg\{\sum {f_{2m} f_{3m}^{'} J_{m} J_{m}^{'} } \sin [\varPhi_{3m} - \varPhi_{2m} + kz(\cos \theta^{'} - \cos \theta )] + \hfill \\ &\sum {g_{2m} g_{3m}^{'} J_{m} J_{m}^{'} } \sin [\varPsi_{3m} - \varPsi_{2m} + kz(\cos \theta^{'} - \cos \theta )]\bigg\} \hfill \\ &\times r{\text{d}}r{\text{d}}\theta^{'} {\text{d}}\theta , \hfill \\ \end{aligned}$$

(8a)

$$\begin{aligned} &\zeta_{y} (z) \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{\infty } } } \hfill \\ &\bigg\{\sum {f_{3m} f_{1m}^{'} J_{m} J_{m}^{'} } \sin [\varPhi_{1m} - \varPhi_{3m} + kz(\cos \theta^{'} - \cos \theta )] + \hfill \\ &\sum {g_{3m} g_{1m}^{'} J_{m} J_{m}^{'} } \sin [\varPsi_{1m} - \varPsi_{3m} + kz(\cos \theta^{'} - \cos \theta )]\bigg\} \hfill \\ &\times r{\text{d}}r{\text{d}}\theta^{'} {\text{d}}\theta , \hfill \\ \end{aligned}$$

(8b)

$$\begin{aligned} &\zeta_{z} (z) \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{\infty } } } \hfill \\ &\bigg\{\sum {f_{1m} f_{2m}^{'} J_{m} J_{m}^{'} } \sin [\varPhi_{2m} - \varPhi_{1m} + kz(\cos \theta^{'} - \cos \theta )] + \hfill \\ &\sum {g_{1m} g_{2m}^{'} J_{m} J_{m}^{'} } \sin [\varPsi_{2m} - \varPsi_{1m} + kz(\cos \theta^{'} - \cos \theta )]\bigg\} \hfill \\ &\times r{\text{d}}r{\text{d}}\theta^{'} {\text{d}}\theta , \hfill \\ \end{aligned}$$

(8c)

where $J^{\prime}_{m}$  = J _m (kr sin θ′), $f^{\prime}_{nm}$ = f _nm (θ′), $g^{\prime}_{nm}$ = g _nm (θ′) (n = 1, 2, 3).

Obviously, ζ _z (z) will be zero if $f_{1m} f^{\prime}_{2m} = g_{1m} g^{\prime}_{2m} = 0$, which implies that the focal field without longitudinal SAM can be obtained if x and y components of the exit pupil field $\vec{E}_{o} (\theta ,\phi)/\!\sin\theta$ do not have the same order of sinusoidal or cosinoidal components. With the same method, we can control whether ζ _x (z) and ζ _y (z) exist.

It should be pointed out that Eq. 8 is a general conclusion to get a focal field with purely transverse SAM. When a desired $\vec{E}_{o} (\theta ,\varphi )$ is determined, the related $\vec{E}_{i} (\theta ,\varphi )$ can be calculated easily.

$${\mathbf{A}}(\theta ,\varphi )\left[ \begin{aligned} \sin \theta P(\theta )E_{1} (\theta ,\varphi ) \hfill \\ \sin \theta P(\theta )E_{2} (\theta ,\varphi ) \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} E_{x} (\theta ,\varphi ) \hfill \\ E_{y} (\theta ,\varphi ) \hfill \\ E_{z} (\theta ,\varphi ) \hfill \\ \end{aligned} \right]$$

(9)

The right-hand side of Eq. 9 is Cartesian components of $\vec{E}_{o} (\theta ,\varphi )$. A focal field which can only be obtained when Eq. 9 have a solution. If $\overrightarrow {{E_{i} }} (\theta ,\varphi )$ exists, the unique solution, owing to rank(A) = 2, can be expressed as:

$$\left[ \begin{aligned} E_{1} (\theta ,\varphi ) \hfill \\ E_{2} (\theta ,\varphi ) \hfill \\ \end{aligned} \right] = \frac{{({\mathbf{A}}^{T} {\mathbf{A}})^{ - 1} {\mathbf{A}}^{T} \overrightarrow {{E_{o} }} (\theta ,\varphi )}}{P(\theta )\sin \theta } = \frac{{{\mathbf{A}}^{T} \overrightarrow {{E_{o} }} (\theta ,\varphi )}}{P(\theta )\sin \theta }.$$

(10)

Considering rank(A) = 2, the existence of the solution of Eq. 9 is equivalent to that the determinant of the augmented matrix (${\mathbf{A}}|\overrightarrow {{E_{o} }} (\theta ,\varphi )$) is zero, which can be expressed in detail as Eq. A1 in the “Appendix”.

3 Configuration and numerical simulation

According to the theory above, we choose a proper $\vec{E}_{o} (\theta ,\varphi )$ expressed as Eq. 11 and the corresponding $\vec{E}_{i} (\theta ,\varphi )$ is Eq. 12.

$$\begin{aligned} &\overrightarrow {{E_{o} }} (\theta ,\varphi ) = \sin \theta \cos \theta (i\cos \varphi + \cos 2\varphi )\overrightarrow {{e_{x} }} \hfill \\ &\quad + \sin \theta \cos \theta (i\sin \varphi + \sin 2\varphi )\overrightarrow {{e_{y} }} + \sin^{2} \theta (i + \cos \varphi )\overrightarrow {{e_{z} }} , \hfill \\ \end{aligned}$$

(11)

$$\begin{aligned} &\overrightarrow {{E_{i} }} (\theta ,\varphi ) = [(i\cos \varphi + \cos^{2} \varphi - \sin^{2} \varphi \cos \theta )\overrightarrow {{e_{x} }} \hfill \\ &\quad + (i\sin \varphi + \sin \varphi \cos \varphi + \sin \varphi \cos \varphi \cos \theta )\overrightarrow {{e_{y} }} ]/P(\theta ). \hfill \\ \end{aligned}$$

(12)

We consider three factors to choose Eq. 11 as. First, $\vec{E}_{o} (\theta ,\varphi )$ must have more than one order number m to get a focal field with purely transverse SAM. Otherwise the transverse SAM will be zero. Second, it is better to choose small order numbers, m, to get a smaller focal spot. Besides, transverse orthogonal components of $\vec{E}_{o} (\theta ,\phi )$ should not have substantial difference, otherwise full-width at half-maximum (FWHM) of two orthogonal direction at the focal plane will have a significant difference, which results in an irregular focal spot. Hence, Eq. 11 is a suitable choice that meets the above conditions although it is not the only one.

The incident field of Eq. 12 can be further optimized. We choose a three-belt binary optical phase plate to encode it to reduce the size of the focal spot and expand the depth of focus. The phase plate can enhance the longitudinal component of the focal field. Hence, the size of the focal spot can be reduced and the depth of focus can be expended [12]. The optical phase plate is set on the lens aperture as shown in Fig. 2. Accordingly, P(θ) in the equations above should be replaced by T(θ)P(θ), where T(θ) is expressed as:

Fig. 2

The three-belt binary optical phase plate. θ ₁ = 0.427 ≈ 24.47°, θ ₂ = 0.735 ≈ 42.11°, θ ₃ = θ _max = arcsin(NA) = arcsin(0.95) ≈ 71.81°

$$T(\theta ) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {for\;0 \le \theta {\text{ < }}\theta _{1} ,\theta _{2} \le \theta {\text{ < }}\theta _{3} } \hfill \\ { - 1,} \hfill & {for\;\theta _{1} \le \theta {\text{ < }}\theta _{2} } \hfill \\ \end{array} } \right.$$

(13)

The binary optical phase plate is employed to split the range of integration and recalculate the algebraic sum of every segmentation. It only changes the distribution of the energy density and the SAM density, while maintaining the same symmetry. Therefore, using annular 0/π phase plates still maintains purely transverse spin of the focal field. If the number of belts is increased, a better optimized result can be acquired at the expense of enhancing calculating complexity.

According to Eqs. 1, 6, 12 and 13, the result of numerical simulation is shown in Figs. 3, 4, 5. Figure 3a–f shows Cartesian components of the SAM density distribution at the focal region of z = 0 and z = λ. The density calculated by Eq. 6, as shown in Fig. 3, is proportional to the theoretical SAM density. It should be noted that Fig. 3c shows s _z is completely vanishing at the focal plane, since E _x and E _y have the same phase while E _z has a phase difference of π/2 at the focal plane. When leaving the focal plane, the polarization of electric field becomes very complex and s _z is no more a constant. From Fig. 3a–f, it is shown that s _x is symmetric with respect to y-axis [i.e., s _y (r, ϕ, z) = s _y (r, − ϕ, z)] while s _x and s _z are antisymmetric [i.e., s _x (r, ϕ, z) = − s _x (r, − ϕ, z), s _z (r, ϕ, z) = − s _z (r, − ϕ, z)], which implies that components in x and z directions of the SAM are zero at the focal region while that in y-direction is not. Therefore, it can be concluded that a focal field with purely transverse SAM is obtained.

Fig. 3

Cartesian components of the SAM density distribution at the focal region for z = 0 (a–c) and z = λ (d–f). They have the same symmetry as Eqs. A5, A6, A7

Fig. 4

Normalized energy density distribution at the focal plane

Fig. 5

Normalized energy density distribution along three orthogonal directions through the maximum energy density at the focal plane

Figure 4 shows normalized energy density at the focal plane and the obtained focal spot is approximately a circle near the maximum energy density. The shape of focal spot does not need to be considered when incident beam is cylindrical polarization, as it must be round. However, a focal field with transverse SAM loses circular symmetry and its shape usually becomes irregular [7], which is not suitable for realistic applications. Hence, it is worthwhile to obtain a proximate round spot with purely transverse SAM.

Figure 5 shows normalized energy density along three orthogonal directions through the maximum energy density at the focal plane. The maximum energy density has a shift of 0.164λ along the x-axis, which is a proof of transverse spin. The FWHM of the focal spot is 0.42λ along the x-axis and 0.46λ along the y-direction. A focal spot with a sub-half-wavelength lateral size is acquired. In terms of depth of focus (i.e., longitudinal FWHM), we achieve a depth of focus of 3.4λ. Specially, a “flattop” energy density distribution can be observed around the maximum. The length of the “flattop” is about 1.2λ. If the uniformity tolerance can be adjusted to 0.9, the corresponding length will become 2.4λ. Moreover, the three-belt binary optical plate can be adjust to fit different applications. For example, to realize 3-D tight focusing, it is better to set θ ₁ = 0.739 and θ ₂ = 0.927. As a result, the FWHM of the focal spot is 0.520λ along x-axis, 0.573λ along y-direction and 1.152λ along z-direction. The corresponding focal volume is estimated to be 0.180λ ³, which is smaller than 0.222λ ³ in the literature [7] with the same NA.

4 Conclusion

In this paper, we theoretically demonstrate that optical focus fields with purely transverse SAM can be obtained when a kind of special incident fields are focused by a high NA AL, and use of binary optical phase plates does not change the characteristics of purely transverse spin. Finally, a sub-half-wavelength focal spot with purely transverse SAM and 3.4λ-length depth of focus is obtained. The method to design special optical fields in our work may be applied in single molecular imaging, optical tweezers and particle manipulation.

Appendix

• 1. Detailed expression of det ($A|\overrightarrow {{E_{o} }} (\theta ,\varphi )$) = 0:

  $$\left\{ \begin{aligned} \varPhi_{1,2a} = \varPsi_{2,2b} = \varPhi_{3,2c + 1} (\forall a,b,c \in N) \hfill \\ \varPhi_{1,2a + 1} = \varPsi_{2,2b + 1} = \varPhi_{3,2c} (\forall a,b,c \in N) \hfill \\ \varPsi_{1,2a} = \varPhi_{2,2b} = \varPsi_{3,2c + 1} (\forall a,b,c \in N) \hfill \\ \varPsi_{1,2a + 1} = \varPhi_{2,2b + 1} = \varPsi_{3,2c} (\forall a,b,c \in N) \hfill \\ \sin \theta (f_{11} + g_{21} ) = 2\cos \theta f_{30} \hfill \\ \sin \theta (2f_{10} + f_{12} + g_{22} ) = 2\cos \theta f_{31} \hfill \\ \sin \theta (g_{12} + 2f_{20} - f_{22} ) = 2\cos \theta g_{31} \hfill \\ for\;n = 2,3,4 \cdots \hfill \\ \sin \theta (f_{1,n - 1} + f_{1,n + 1} - g_{2,n - 1} + g_{2,n + 1} ) = 2\cos \theta f_{3,n} \hfill \\ \sin \theta (g_{1,n - 1} + g_{1,n + 1} + f_{2,n - 1} - f_{2,n + 1} ) = 2\cos \theta g_{3,n} \hfill \\ \end{aligned} \right..$$

  (A1)

• 2. Electric field and SAM density corresponding to $\vec{E}_{i} (\theta ,\varphi )$ in Eq. (12):

$$\begin{aligned} E_{x} (r,\phi ,z) &= - ik\int_{0}^{{\theta_{\hbox{max} } }} {(\cos \phi J_{1} + \cos 2\phi J_{2} )} \hfill \\ &\quad \times\sin \theta \cos \theta \exp (ikz\cos \theta ){\text{d}}\theta , \hfill \\ \end{aligned}$$

(A2)

$$\begin{aligned} E_{y} (r,\phi ,z) &= - ik\int_{0}^{{\theta_{\hbox{max} } }} {(\sin \phi J_{1} + \sin 2\phi J_{2} )} \hfill \\ &\quad\times \sin \theta \cos \theta \exp (ikz\cos \theta ){\text{d}}\theta , \hfill \\ \end{aligned}$$

(A3)

$$\begin{aligned} E_{z} (r,\phi ,z) &= - k\int_{0}^{{\theta_{\hbox{max} } }} {(J_{0} + \cos \phi J_{1} )} \hfill \\ &\quad\times \sin^{2} \theta \exp (ikz\cos \theta ){\text{d}}\theta , \hfill \\ \end{aligned}$$

(A4)

$$\begin{aligned} &s_{x} \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\sin \theta \cos \theta \sin^{2} \theta^{'} (\sin \phi J_{1} + \sin 2\phi J_{2} )} } \hfill \\ &\quad \times (J_{0}^{'} + \cos \phi J_{1}^{'} )\cos [kz(\cos \theta^{'} - \cos \theta )]{\text{d}}\theta^{'} {\text{d}}\theta , \hfill \\ \end{aligned}$$

(A5)

$$\begin{aligned} s_{y} \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\sin^{2} \theta \sin \theta^{'} \cos \theta^{'} (J_{0} + \cos \phi J_{1} )} } \hfill \\ \times\;\;\;(\cos \phi J_{1}^{'} + \cos 2\phi J_{2}^{'} )\cos [kz(\cos \theta^{'} - \cos \theta )]{\text{d}}\theta^{'} {\text{d}}\theta , \hfill \\ \end{aligned}$$

(A6)

$$\begin{aligned} &s_{z} \propto \int_{0}^{{\theta_{\hbox{max} } }} {\int_{0}^{{\theta_{\hbox{max} } }} {\sin \theta \cos \theta \sin \theta^{'} \cos \theta^{'} (\cos \phi J_{1} + \cos 2\phi J_{2} )} } \hfill \\ &\times\, (\sin \phi J_{1}^{'} + \sin 2\phi J_{2}^{'} )\sin [kz(\cos \theta^{'} - \cos \theta )]{\text{d}}\theta^{'} {\text{d}}\theta . \hfill \\ \end{aligned}$$

(A7)