1 Introduction

Fiber Bragg gratings (FBGs) based devices are used in a wide range of applications in the areas of optical communications such as filters and dispersion compensators [1, 2], and sensors [3] for measuring strain [4, 5], stress [6] and vibrations [7, 8], acoustic pressure (hydrophone) [9, 10], temperature [11], gamma-radiation effects on temperature sensing FBG [12], static displacement [13], force [14], ambient refractive index [15], and simultaneous measurement of temperature and strain [16].

Long et al. reported a simultaneous measurement of temperature and stress using an embedded FBG sensor [17]. Lu et al. analyzed cross sensitivity of an FBG with different polymeric coatings [18]. Park et al. proposed a poly-FBG temperature sensor using dimethylsiloxane coated for enhancing temperature sensitivity [19]. Recently, an experimental investigations on hydrostatic pressure sensitivity of single-mode polymer fiber Bragg grating with different diameters are reported [20].

The transverse strains, produced by environmental factors such as temperature [21], can change the refractive index of fiber core, resulting in birefringence [22, 23], and thus varying the reflecting Bragg wavelength \(\lambda_{\text{B}}\) [5, 24]. Therefore, due to the birefringence, there will be two modes in the reflecting wavelengths. When the lateral pressure exerting on the FBG increases, the distance between two modal peaks widens more [25].

Jewart et al. presented simulation and experimental results of fiber Bragg grating responses to transverse stress in microstructure fibers. It was shown that the sensitivity of grating sensors to the transverse stress can be enhanced by a factor of eight in a two-hole fiber over that in a standard fiber [5].

In another report, Moccia et al. carried out a numerical analysis of the response of an underwater-acoustic wave sensor by using FBG coated by ring-shaped overlays. It was shown that the coating may significantly enhance the sensitivity over the whole investigated frequency range, by comparison with an uncoated FBG. The coating height and radius may be used to tune the resonant frequencies and improve the low-frequency background sensitivity. Further, it was indicated that the low values of the Young’s modulus, Poisson’s ratio are desirable to enhance the sensitivity [9]. Experimentally it was shown that by comparison with uncoated FBGs, responsivity was enhanced up to three orders of magnitude indicating the effects of polymeric coatings on the acoustic response of FBG-based hydrophones [10].

In our previous analysis of the effect of temperature rise and hydrostatic pressure on refractive index and stress components of a double-coated conventional single-mode optical fiber was reported by considering coating material parameters such as Young’s modulus and the Poisson ratio. It was shown that by rising temperature, the core refractive index would decrease with the increase of the thickness of primary coating layer and would increase after passing through a minima. Increase of thickness of secondary coating layer would cause the core refractive index to decrease. The increase of Young’s modulus and the Poisson ratio of primary coating would lower the core refractive index change whereas in the secondary coating layer, the condition reverses [26].

With reference to the importance of previous reports [5, 9, 10, 26], in this paper, by considering FBGs with double-coating of primary and secondary with soft and hard polymers, respectively, we have analyzed the effects of thermal loading and hydrostatic pressure on Bragg reflecting wavelengths of the double-coated FBGs by varying primary and secondary coating-layer thicknesses with a given elastic properties of the materials The core and cladding of the FBG are assumed to be doped by GeO2 and B2O3, respectively [27,28,29,30].

2 Fundamental formulations

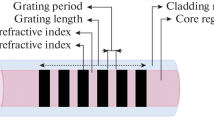
Due to periodic variations of the refractive index of FBG core, the forward propagating light reflects back with a Bragg grating wavelength \(\lambda_{\text{B}}\) given as:

$$\lambda_{\text{B}} = 2n_{\text{eff}} \varLambda ,$$
(1)

where \(n_{\text{eff}}\) is the effective refractive index of the fiber core, \(\varLambda\) is the grating pitch, as shown in Fig. 1 [7].

Fig. 1
figure 1

Schematic of a double-coated fiber Bragg grating

Full size image

When the FBG is affected by some external factors, due to changes in core effective index, there will be a change in the Bragg wavelength. In case of no axial strain applying on FBG and no shear stress, the wavelength variation along x and y axes are given, respectively, as [25]:

$$\Delta \lambda_{{{\text{B,}}x}} = - \frac{{n_{\text{eff}}^{3} \varLambda }}{E}\left\{ {\left. {\left( {p_{11} - 2\nu p_{12} } \right)\sigma_{x} + \left[ {\left( {1 - \nu } \right)p_{12} - \nu p_{11} } \right]\left[ {\sigma_{y} + \sigma_{z} } \right]} \right\}} \right.,$$
(2)
$$\Delta \lambda_{{{\text{B,}}y}} = - \frac{{n_{\text{eff}}^{3} \varLambda }}{E}\left\{ {\left. {\left( {p_{11} - 2\nu p_{12} } \right)\sigma_{y} + \left[ {\left( {1 - \nu } \right)p_{12} - \nu p_{11} } \right]\left[ {\sigma_{x} + \sigma_{z} } \right]} \right\}} \right.,$$
(3)

where \(p_{11}\) and \(p_{12}\) are elastooptic constants of the core, respectively, \(E\), \(v\) indicate Young’s modulus and Poisson ratio, and \(\sigma_{x}\), \(\sigma_{y}\), and \(\sigma_{z}\) are stresses along x, y, and z axes, respectively [25, 31].

Let us consider double-coated FBG as a cylindrical structure with an internal and external diameters of a and b, respectively, which is exposed to a thermal variation of \(\Delta T\) and respective internal and external pressure of \(P_{\text{i}}\) and \(P_{\text{e}}\), as shown in Fig. 2 [32].

Fig. 2
figure 2

FBG cylindrical structure with internal \(a\) and external \(b\) diameters under a thermal variation of \(\Delta T\), internal \(P_{\text{i}}\), and external \(P_{\text{e}}\) pressures

Full size image

By assuming an axial symmetry and a constant thermal variation across the structure, the \(\varepsilon_{\theta }\) tangential strain in the structure with zero axial strain is given as [33,34,35,36]:

$$\varepsilon_{\theta } \, = \frac{u}{r}\, = \, \pm \alpha \,\Delta T\,(1 + \nu ) + \frac{{(1 - \nu^{2} )}}{E}\,\left( {\sigma_{\theta } \, - \,\frac{\nu }{1 - \nu }\,\sigma_{r} } \right),$$
(4)

where \(u\) indicate the radial variation and \(r\) is the radius of the layer, \(\alpha\) is the thermal expansion coefficient. By applied pressure of \(P_{\text{e}}\) and \(P_{\text{i}}\), in Fig. 2, the respective tangential \(\sigma_{\theta }\), radial \(\sigma_{r}\), and axial \(\sigma_{z}\) stresses can be derived by Lamé formula [26, 36].

In all the above expressions, the plus and minus signs of \(\Delta T\) represent a decrease and an increase in temperature, respectively [26]. By inserting \(\sigma_{\theta }\) and \(\sigma_{r}\) in (4), we obtain:

$$\begin{aligned} u &= \, \pm \alpha \,\Delta T\,(1 + \,\nu )\,r\, + \,\frac{1 + \nu }{{E\,(1 - \xi^{2} )}}\,[\,(1 - 2\nu )\,(P_{\text{i}} \,\xi^{2} \, - \,P_{\text{e}} )\, \\ & \quad \times r\, - \,a^{2} \,(P_{\text{e}} \, - \,P_{\text{i}} \,)\,/\,r], \end{aligned}$$
(5)

where \(\xi = a/b\) is the radius ratio of the structure [26, 33].

The general expression for the displacement at the layers interfaces in case of additional coating layers applied on the structure can be shown as [26]:

$$\begin{aligned} u_{i,i + 1} &= \, \pm \,\alpha_{i} \,\Delta T\,(1 + \nu_{i} )\,r_{i} \, + \frac{{(1 + \nu_{i} )\,r_{i} }}{{E_{i} \,(1 - \xi_{i}^{2} )}}\,[(1 - 2\,\nu_{i} )\, \\ & \quad \times (P_{i} \,\xi_{i}^{2} \, - \,P_{i + 1} ) - \,\xi_{i}^{2} \,(P_{i + 1} \, - \,P_{i} )], \end{aligned}$$
(6)
$$\begin{aligned} u_{i + 1,i} & = \, \pm \alpha_{i + 1} \,\Delta T\,\left( {1 + \nu_{i + 1} } \right)\,r_{i} + \,\frac{{\left( {1 + \nu_{i + 1} } \right)\,r_{i} }}{{E_{i + 1} \,\left( {1 - \xi_{i + 1}^{2} } \right)}} \\ & \quad \times \left[ {\left( {1 - 2\,\nu_{i + 1} } \right)\,\left( {P_{i + 1} \,\xi_{i + 1}^{2} \, - P_{i + 2} } \right) - \,\left( {P_{i + 2} - P_{i + 1} } \right)} \right], \\ \end{aligned}$$
(7)

where \(u_{i + 1,\,i}\) represents the displacement of (i + 1)th layer at the interface of ith layer and \(u_{i,i + \,1}\) indicates the displacement of ith layer at the interface with (i + 1)th layer. The value of \(i\) varies from zero to maximum value of \(i_{\hbox{max} }\) (no. of layers − 1). \(P_{i}\) is the lateral pressure between the (i − 1)th and i layers, \(P_{i + 1}\) the lateral pressure between ith and (i + 1)th layers, \(P_{i + 2}\) the lateral pressure between (i + 1)th and (i + 2)th layers, and \(\xi_{i + 1} = r_{i} /r_{i + 1}\). Whenever \(i = i_{\hbox{max} }\), the pressure \(P_{i + 2}\) will be considered as the hydrostatic external pressure exerted on the structure.

In a general case, determination of \(u_{i + 1,\,i}\) and \(u_{i,\,i + 1}\) continues up to the desired layer. At the interfaces between the layers, the displacements of the layers are equal. Therefore, by equating \(u_{i + 1,\,i}\) and \(u_{i,\,i + 1}\) at the interface \(r = r_{i}\), the exerting pressures on different layers and the fiber itself in terms of thermal variation and hydrostatic pressure (HSP) is obtained as [26]:

$$P_{1} = (\lambda_{{i_{\text{max} } }} \,P \mp M_{{i_{\text{max} } }} \,\Delta T)/N_{{i_{\text{max} } }} ,$$
(8)
$$P_{i + 2} = (N_{i} P_{1} \pm M_{i} \Delta T)/\lambda_{i} ,\,\,\,\,\,i = \, 0,1,2, \ldots , \, i_{\text{max} } - 1,$$
(9)

where \(M_{i}\) and \(N_{i}\), and other parameters depending on the parameters defined in (6) and (7) (for details see [26]). The indices \(i = 0,\,1,\,2,\,3\) represent the core, the cladding, the primary, and the secondary coating layers, respectively. For \(i = 2\) and \(P_{i} = P_{1}\), the exerted lateral pressure on the core of a FBG coated with a soft and a hard layer is obtained by \(P_{1} = (\lambda_{2} P \mp M_{2} \Delta T)/N_{2} \,\) [26]. The radial, the tangential, and the axial stresses exerted on the FBG, with respect to internal pressure \(P_{\text{i}}\) and zero internal core radius, will be [26, 33]:

$$\sigma_{r} = \sigma_{\theta } = - P_{1} ,\,\,\,\,{\text{for}}\,\,r \le r_{0} ,$$
(10)
$$\sigma_{z} = \pm E_{0} \alpha_{0} \Delta T - 2\nu_{0} P_{1} ,\,\,\,\,\,{\text{for}}\,\,r \le r_{0} .$$
(11)

To determine the variations of reflected Bragg wavelength along \(x\) and \(y\) directions, we should calculate the stresses at the fiber surface expressed in (2) and (3).

By assuming that the exerted pressure and the thermal variations have axial symmetry, and the lateral pressure on FBG has a constant value for all values of \(\theta\), then we note that \(\sigma_{x}\) and \(\sigma_{y}\) will be equal to \(\sigma_{r}\) and hence equal to \(\sigma_{\theta }\). Moreover, since cylindrical coordinate is used, the component \(\sigma_{z}\) is the same in both cases. Therefore, we can write the reflected Bragg wavelength change from (2) and (3) as follows:

$$\begin{aligned} \Delta \lambda_{{{\text{B}},x}} & = \Delta \lambda_{{{\text{B}},y}} = - \frac{{n_{\text{eff}}^{3} \varLambda }}{{E_{0} }}\left\{ { - \left( {p_{11} - 2\nu_{0} p_{12} } \right)P_{1} + \left[ {\left( {1 - \nu } \right)p_{12} - \nu p_{11} } \right]} \right. \\ & \quad \left. {\, \times \,\left[ { \pm E_{0} \alpha_{0} \Delta T - \left( {1 + 2\nu_{0} } \right)P_{1} } \right]} \right\}. \\ \end{aligned}$$
(12)

With equal reflected Bragg wavelength changes, we can say that under the present condition, the refractive index change along \(x\) and \(y\) directions are the same, hence resulting in no birefringence, and only single peak-splitting will occur against HSP and thermal variation [25].

3 Numerical calculations and discussions

In our calculations and simulations, the effects of primary and secondary layer thicknesses, hydrostatic pressure, and thermal loadings on reflected Bragg wavelength of FBG with specifications given in Table 1 are considered [5, 25]. In the cases when the HSP and the thermal loadings (increasing/decreasing modes) are constants, the values of 0.5 MPa and 1 °C are used, respectively.

Table 1 Geometrical and physical parameters of double-coated FBG [5, 25]
Full size table

3.1 Decrease in temperature loading

The effects of thickness variations of primary coating layer and decreasing thermal variations on Bragg wavelength shift is shown in Fig. 3 for different temperature variations from \(\Delta T = 1\,{^\circ }{\text{C}}\) to \(\Delta T = 20\,{^\circ }{\text{C}}\).

Fig. 3
figure 3

The effects of thickness variations of primary coating layer and decreasing thermal variations on Bragg wavelength shift

Full size image

For any decrease in thickness of primary coating layer, the variation of Bragg wavelength shift \(\lambda_{\text{B}}\) along \(x\) and \(y\) directions would increase at a specified temperature loading. As it is observed in the lower range of thickness of primary coating layer less than \(r_{2} = 155\) μm, an increase in reduction of thermal variations would cause a decrease in \(\lambda_{\text{B}}\). But, from a given thickness more than \(r_{2} = 155\) μm as a turning point, changes the trend and an increase in temperature would reverse the effects on \(\lambda_{\text{B}}\), as illustrated in Fig. 3. After temperature reduction of more than 15 °C, from the thickness of about \(177\) μm onwards, the Bragg wavelength shift will set to negative values, indicating a up-shift in the Bragg wavelength.

The effects of variations of secondary coating layer thickness \(r_{3}\) and reduction in temperature variations \(\Delta T\) on \(\lambda_{\text{B}}\) are shown in Fig. 4. Here, the increase of temperature reduction and higher thickness values would cause decrease in \(\lambda_{\text{B}}\). Similar to the case of primary coating layer (see Fig. 3), the down-shifting of the Bragg wavelength will occur by increasing the temperature reduction and secondary coating layer, i.e., higher the temperature reduction, more will be the down-shift of Bragg wavelength. At about \(r_{3} = 224\) μm and \(\Delta T > 20\,{^\circ }{\text{C}}\), the Bragg wavelength shift changes sign, indicating an up-shift in the wavelength.

Fig. 4
figure 4

The effects of secondary coating layer thickness on Bragg wavelength shift at different temperatures reduction

Full size image

The effects of primary and secondary coating thicknesses, and HSP in presence of temperature reduction of 1 °C on Bragg wavelength shift are illustrated in Fig. 5. An increase in the primary and the secondary coating layers thicknesses and a decrease in HSP would cause a reduction in the Bragg wavelength. For constant primary/secondary coatings thicknesses, when the HSP on FBG increases, the shift in Bragg wavelength would increase. Recently, the same result is reported experimentally for a polymer optical fiber Bragg grating [20].

Fig. 5
figure 5

Bragg wavelength shifts versus HSP with a primary, and b secondary coating layers at temperature reduction with step of 1 °C

Full size image

3.2 Increase in temperature loadings

Similar to the previous discussions, in case of the rise of temperature loading and thickness variations of the primary coating layer, there will again be some effects on the Bragg wavelength shift. When temperature loading is at 1 °C, the Bragg wavelength shift \(\lambda_{\text{B}}\) decreases exponentially with the primary coating layer and at 2 °C, the exponential increase is mild. These two variation trends continues up to a turning point at \(r_{2} = 155\) μm, beyond which the \(\lambda_{\text{B}}\) variations will increase almost linearly, as depicted in Fig. 6.

Fig. 6
figure 6

The Bragg wavelength shifts as a function of primary coating layer thickness for different temperature increase

Full size image

Prior to this value of the layer thickness \(r_{2}\), the temperature increase has a steep decreasing effect on the wavelength shift and beyond that value, the effect of increasing temperature on \(\lambda_{\text{B}}\) will be with a milder slope.

As illustrated in Fig. 7, at lower temperature change, an increase in secondary layer thickness causes a reduction in Bragg wavelength shift, while at higher temperature variations, the wavelength shift will increase [20].

Fig. 7
figure 7

Bragg wavelengths shift as functions of secondary coating layer thickness and temperature

Full size image

At a constant temperature variation of 1 °C, when the HSP and secondary coating increase, Bragg wavelength shift increases for a constant value of primary coating layer thickness, as illustrated in Fig. 8. At lower hydrostatic pressures, the down-shift in Bragg wavelength occurs. At a given HSP and under the same temperature condition, an increase in primary coating thickness would cause a reduction in Bragg wavelength shift. The variation of Bragg wavelength shift as function of HSP and the thickness of secondary coating layer is similar to primary coating layer case, as shown in Fig. 8.

Fig. 8
figure 8

Bragg wavelength shifts versus HSP a primary, and b secondary coating layers at temperature increase with a step of 1 °C

Full size image

For every step increase of temperature by 1 °C, the trend of reduction in Bragg wavelength continues up to layer thickness of 180 μm. Beyond this thickness, the wavelength shift becomes negligible and from 2 °C onwards, the wavelength shift becomes more sensible.

4 Conclusion

This paper presented design criteria of double-coated fiber Bragg grating based on analysis on variations effects of coating-layer thickness and thermal loading (increase/decrease) on reflecting Bragg wavelength shifts.

The analysis has shown that when temperature decreases and the primary coating layer increases, the Bragg wavelength shift along radial and tangential directions reduces. In lower primary coating layer thickness, a reduction in temperature variation would cause an increase in Bragg wavelength shift in two directions. After a certain layer thickness of the primary coating, this trend changes, i.e., by decreasing the temperature variations, the Bragg wavelength shift would decrease.

In secondary coating layer, temperature reduction and layer thickness increase cause the Bragg wavelength shift to reduce. In primary coating layer, at temperature higher than 5 °C, when the layer thickness increases, the Bragg wavelength shift would increase. Moreover, prior to certain layer thickness, increase of temperature variation will limit the shift of Bragg wavelength and beyond this thickness value, an opposite case occurs. As the temperature variation goes higher, a down-shift is imposed on Bragg wavelength.

In secondary coating layer, increase in layer thickness would reduce the Bragg wavelength shift whereas increase in temperature variation and applied hydrostatic pressure on FBG would have increasing impact on Bragg wavelength shift.

The results obtained in our analyses may be utilized in the design of pressure sensors when using double-coated fiber Bragg grating.