1 Introduction

Laser diode (LD) pumped solid-state lasers have been widely studied for their high efficiency, small footprint, and high beam quality [1]. The high pump intensity and good overlap between the pump and the laser modes make LD end-pumped slab lasers attractive candidates that can realize high gain and good beam quality, simultaneously. Because of the small difference between the pump and laser photon energies, the fractional thermal load of Yb:YAG crystal (pump at 940 nm and lasing at 1030 nm) is more than three times smaller than that of Nd:YAG (pump at 808 nm and lasing at 1064 nm) counterparts. [2], thus resulting in less heat generation for high-power operation. In 1993, the first diode-pumped Q-switched Yb:YAG laser was reported by T.Y. Fan [3]. In 1998, Du demonstrated the principle of a partially end-pumped Yb:YAG laser [4], and good mode selection along the slab thickness direction was achieved. Subsequently, high-power and high-energy lasers were reported, based on using a partially end-pumped slab gain medium [5,6,7,8], which displayed great potential for pulse laser and amplification in the femto to nanosecond range. Robust Yb:YAG lasers, featuring high beam quality and high efficiency, operating at repetition rates below 1 kHz and pulse energies exceeding 10 mJ, have applications in airborne and space-borne communication systems.

The thermal issues currently limit the performance of high-power and high-energy lasers based on Yb as the active ion. The thermal effect in high-power laser has been well studied [9,10,11,12,13,14], but the thermal effect on low repetition rate and high-energy laser needs more investigation. The steady-state thermal distribution over the cross sections of various slab structures has been analytically and numerically analyzed for different gain media [9,10,11,12,13,14]. Typically, it takes a relatively long time for the thermal distribution in a laser gain medium to reach steady-state conditions [15]. The thermal distribution in pulsed lasers has occasionally been analyzed by assuming these lasers as continuous-wave lasers (i.e., a pulse pump laser is assumed to be equivalent to a continuous pump laser). For this approach, the thermal distribution in the pulsed laser medium is considered invariable, i.e., at steady state. However, a Q-switched pulsed laser or pulsed laser amplifier always generates an output signal after the application of the pump pulse. To attain high gain and high pump efficiency, the pump duration typically has to be equal to the lifetime of the upper-level of the Yb:YAG laser system [16]. The typical pumping duration for Yb:YAG is about 1 ms, which is too short for the slab gain medium to reach steady state [15]; thus, at the fall-edge of the pump pulse, the thermal distribution in a laser medium does not reach a steady state. Therefore, the transient thermal distribution and effect should be investigated.

Thermal distribution in the optical gain medium mostly affects the laser operation mode through three main phenomena [17], namely (1) refractive index variation due to temperature rise, (2) surface bulging due to thermal expansion, and (3) stress-induced birefringence due to the photo-elastic effect. For a slab laser structure employing conductive cooling through the two large faces of the slab medium, the thermal gradient over the slab’s cross section is typically high, with the highest temperature being in the center of the slab. The gradual thermal distribution along the fast axis results in thermal lensing effects. In laser oscillators, thermal lensing would change the laser mode in cavity and the overlap between the laser and pump [18], resulting in reduced efficiency and lower beam quality. In laser amplifiers, the thermal effect would also change the system parameters, posing the risk of formation of focal point on/in the optical components that might damage the optical components of the optical train. Therefore, thermal lensing effects must be thoroughly investigated, and adequate heat sink geometry and configuration must be designed in order to appropriately dissipate the heat load and reduce the temperature and the thermal gradient. The thermally induced optical path difference (OPD) is sometimes referred to as the thermal lensing effect. However, it is important to mention that the thermally induced OPD profile is not an ideal spherical or parabolic distribution, and this affects the laser beam quality and induces aberration in the laser wavefront. These thermal effects cannot be simply described through the thermal lensing effect, and, with a complex pumping scheme, these effects cannot be expressed using simple analytical expressions.

In this paper, the thermally induced beam quality degradation in end-pumped Yb:YAG slab amplifiers operated at low repetition rates and high pump power levels is investigated for single- and double-end pumping, and different slab thicknesses. This kind of Yb:YAG slab could be used in hundred-mJ-level laser amplifier. Transient temperature distribution in slab Yb:YAG gain media operating at a 10-Hz repetition rate and with up to 1 kW pulsed pump is evaluated, and the thermally induced refractive index distribution and thermal lensing effect are numerical simulated. The non-lensing effects in the slab are simulated for different pump power levels and beam widths. This beam quality degradation caused by the non-lensing effects is derived and simulated using Fast Fourier Transform (FFT) methods, which enable the beam quality to be predicted and improved through the use of compensating optical components, hence enabling high-performance laser amplifiers to be developed.

2 Distribution of temperature and optical path difference (OPD)

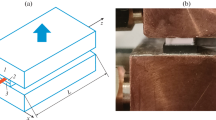
The generic structure of an end-pumped slab Yb:YAG amplifier is shown in Fig. 1. 10 mm × 10 mm Yb:YAG gain slabs of thicknesses 1,1.5, and 2 mm (fast-axis/x-axis direction) and 2.5 at % doping concentration were simulated. The upper and lower faces (10 mm × 10 mm) of the slabs were assumed tightly mounted and connected to water-cooled copper heat sinks with indium foil as thermal interface. The pump and laser wavelengths were assumed to be 940 and 1030 nm, respectively. The single-end pump power level was varied from 600 to 1 kW, making the maximum pump power 2 kW for double-end pump structures. The LD pump laser was uniformly distributed along the slow-axis direction (y-direction) and Gaussian distributed along the fast-axis (x-direction).

Fig. 1
figure 1

Generic structure of an end-pumped slab Yb:YAG amplifier

Full size image

The equation of heat conduction is shown in Eq. 1. In the equation, \(T\) is the temperature distribution in the gain medium. \(k\) is Yb:YAG conductivity, and \(\rho\) and \(c\) are the mess density and special heat of the Yb:YAG crystal, respectively. \(S_{\text{T}}\) is the heat generated in the unit volume.

$$\frac{\partial }{\partial t}\left( {\rho cT} \right) = \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {k\frac{\partial T}{\partial z}} \right) + S_{\text{T}}$$
(1)

The two big surfaces of the slab are tightly mounted to the indium foil and attached to the water-cooled heat sink. The other surfaces are treated as adiabatic boundaries. The equations of heat conduction on the cooling and adiabatic surface are shown as equations:

$$\begin{aligned} k \cdot \left. {\frac{{\partial T}}{{\partial z}}} \right|_{{{\text{cf}}}} \; &= \;\frac{{k_{{{\text{in}}}} }}{d}\left( {T_{{{\text{HS}}}} \; - \;T_{{{\text{cf}}}} } \right),{\text{cooling surfaces}} \hfill \\ k \cdot \left. {\frac{{\partial T}}{{\partial z}}} \right|_{{{\text{other}}}} & = 0,{\text{adiabatic surfaces}} \hfill \\ \end{aligned}$$
(2)

In Eq. 2, the subscript \({\text{cf}}\) indicates the cooling surfaces, and \({\text{HS}}\) indicates heat sink, \(k\) is the conductivity of crystal, \(k_{\text{in}}\) is the conductivity of indium foil, and \(d\) is the thickness of the indium foil.

The equations of heat conduction and boundary conditions are discretized [12]. In our simulation, to obtain the transient temperature distribution, the time in equations is also discretized, and the time-dependent temperature variation is considered. With the obtained temperature distribution, the thermal induced refraction index variation is computed [13]. With maximum slab thickness of 2 mm, the ratio of thickness to length is 1/5. The thermal stress could be computed with basic hypothesis of materials elasticity mechanics and thin plate theory.

Numerical simulation of the thermal distribution in the gain medium was performed using MATLAB software. The parameters used in the simulation are shown in Table 1 [9]. For both oscillator and amplifier pulsed operations, the Q-switched laser pulses were always generated and amplified after the end of the pump pulses. As mentioned above, the pump time duration is too short for the thermal distribution to reach steady state at the end of the pump pulse. Our simulation results show that there is a significant difference between the thermal distribution at steady state and at the end of the pump pulse. For illustration, Figs. 2a, b shows the maximum temperature versus time and distance along the x-axis, respectively, for the 1-mm-thick gain slab, and for pulsed pumping (single-end pump pulses of peak power 1 kW, duration 1000 µs, repetition rate of 10 Hz, and beam width along the x-axis direction 0.4 mm) and CW pumping at 10 W (blue line). The simulation results shown in Fig. 2a, b reveal that (1) the maximum temperature of the slab operating with a pulsed pump is around 2.4 K higher than that attained with a CW pumped slab, and (2) the thermal gradient, at the end of pump pulse is much higher than that for a CW pump slab, resulting in much more thermal stress and higher OPD.

Table 1 Slab amplifier parameters used for the simulation of thermal effects
Full size table
Fig. 2
figure 2

a Simulated maximum temperature versus a time and b distance along the x-axis, for the 1-mm-thick gain slab, for pulsed pumping and CW pumping at 10 W (blue line). c Maximum temperature in the gain slabs versus time for different slab thicknesses. To illustrate the difference between the responses for different slab thicknesses, a 15 ms time interval was introduced. d Maximum temperature that can be attained at the end of the pump pulsed for single-end-Gaussian pumping at 1 kW, for different slab thicknesses

Full size image

Figure 2c shows the maximum temperature in the gain slabs versus time, for different slab thicknesses. Note that, in order to better illustrate the difference between the responses for different slab thicknesses, a 15-ms time interval was introduced in Fig. 2c. Figure 2d shows the simulated maximum temperature attained at the end of the pump pulsed for single-end-Gaussian-pumping at 1 kW, for different slab thicknesses.

It is obvious from Fig. 2 that increasing the slab thickness increases the maximum temperature that can be attained at the end of the pump pulse, and that the time required to reach steady state increases with increasing the slab thickness.

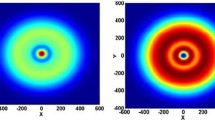
Figure 3 shows the OPD distribution in the x–y plane based on the simulated temperature distribution shown in Fig. 2, for a pump beam width (in the x-axis direction) of 0.4 mm. Figure 4 a shows the OPD versus distance along the x-axis for different slab thicknesses. Figure 4b is a zoom-in of Fig. 4a showing the OPD over the 0.12–0.2 mm range along x-axis. It is obvious from Fig. 3 and Fig. 4a that the maximum OPD is \(1.044\;\lambda\) (red color), which occurs at the center of the slab’s cross section, while Fig. 4b shows that, over the thickness of the slab, the OPD reduces as the slab thickness increases.

Fig. 3
figure 3

Simulated OPD distribution in the x–y plane with the application of a pump pulse. The OPD is simulated at the end of the pump pulse duration. The maximum OPD (red color) is 1.044 \(\lambda\)

Full size image
Fig. 4
figure 4

a Simulated OPD distribution along the x-axis direction for different slab thicknesses. The pump beam width was 0.4 mm. b zoom in image of a

Full size image

The thermal stress results under different pump conditions were computed. The thermal stress results under double-end pump (each end pump power was 1 kW) is shown in Fig. 5. With slab thickness of 2 mm, the maximum thermal stress in y-direction is about 14 Mpa, which is much smaller than the typical fracture limit of ~127Mpa. Also, with same pump width and different slab thickness, maximum stress difference of 2 MPa is observed. So, in our simulation, the changing of pump conditions would not induce the fracture of crystal.

Fig. 5
figure 5

The thermal stress in y-direction under double-end pump with each end pump power of 1 kW. With slab thickness of 2 mm, the maximum thermal stress in y-direction is about 14 Mpa. Thermal stress difference of 2 Mpa is observed with slab thickness of 1 and 2 mm

Full size image

3 Thermal lensing effect and wavefront distortion

The OPD ultimately affects the laser performance through two main phenomena, namely (1) the thermal lensing effect induced thermal focus, and (2) the induced wavefront distortion, which degrades the beam quality. To optimize the performance for high-power laser operation, it is necessary to take both of the above-mentioned phenomena into account. Perfect thermal lensing does not change the beam quality; however, since thermal lensing is typically imperfect, beam quality degradation is experienced.

The refractive index distribution in an LD end-pumped YAG gain medium is typically lens-like [19], which can be described as follows:

$$n(x,y) = n_{0} \left[ {1 - \frac{{k_{2} }}{{2k_{0} }}\left( {x^{2} + y^{2} } \right)} \right]$$
(3)

The OPD distribution over the cross section of the slab is similar to the lens-like distribution expressed in Eq. 3. However, the OPD distribution in the gain medium is typically imperfect (i.e., not lens-like). The one-dimensional thermally induced lensing effect can be expressed using the following approximation [20]:

$${\text{OPD}}\left( j \right) = p_{0} + p_{1} j + p_{2} j^{2} + \cdots + p_{n} j^{n} + \tau (n + 1).$$
(4)

where p 0 is the path length of the ray incident onto the center of the pump face, p 1 is the linear component of path length associated with the optical wedging of the beam (prismatic deviation), p 2 is the second-order coefficient associated with the thermal lensing, and the higher order coefficients, p k of Eq. 4 relate to effective aberration. The second-order term of Eq. 4 represents the dominant lensing effect. The power, D p, of a thermally induced lens of focal length ft is determined by the quadratic part of the OPD function, that is

$$D_{\text{p}} = \frac{1}{{f_{t} }} = - 2p_{2}$$
(5)

In single-end and double-end slab media pumped with Gaussian beams, the peak value of OPD always occurs at the center of the pump, which is also the center of the beam’s Gaussian distribution. The maximum thermal gradient is displayed at the edge of the pump, resulting in maximum thermal-stress-induced OPD. The simulated OPD fits very well with a lens-like profile at the center of the pump region with different pump beam widths along the x-axis direction. Two 1-mm-thick slab samples with 0.4 mm single- and double-end Gaussian pump beam widths were simulated, and their OPDs are shown in Figs. 6a, b, respectively. For the single-end pumping, the pump power was 1 kW, while for the double-end pumping, the pump power of each side was 1 kW. In Fig. 6, both the simulated overall OPD (black solid line) and second-order component of the polynomial fitting (blue dashed line) are shown. To investigate the effect of beam quality degradation, the OPD-induced lensing effect is ignored. The profiles for the OPD without the lensing effect, denoted ΔOPD, are shown as red solid curves in Fig. 6a, b for both the single-end- and double-end- pumped slabs. Near the origin of the x-axis, ΔOPD is almost constant. However, most of the distortion (high ΔOPD) is experienced near the boundaries of the slab (high x values). For the different thicknesses of the slabs, the shapes of the OPD curves look almost similar; but their peak values are different. According to Fig. 6, the OPD for a slab with double-end pumping is approximately twice that of a slab employing single-end pumping.

Fig. 6
figure 6

Simulated OPD distribution along the x-direction for a single-end- and b double-end-pumped slabs. The lensing effect caused by the OPD is represented by the blue dashed curve, and the difference between the actual OPD and the second-order component of the OPD, ΔOPD, is represented by the red curve. Most of the distortion (high ΔOPD) is experienced at the sides of the pump region

Full size image

Figure 7a, b shows the simulated ΔOPD along the x-axis for 1-mm-thick single-end- and double-end-pumped slabs, respectively, for different pump beam widths (namely, 0.1–0.9 mm).

Fig. 7
figure 7

ΔOPD distribution along the x-direction for a single-end- and b double-end-pumped slabs for different pump beam widths (0.1 to 0.9 mm). The maximum ΔOPD value decreases with increasing the pump beam width

Full size image

When considering the overlap between the laser and pump signals, wavefront distortion inside the pump region is the dominant factor that affects the performance of the slab. For example, according to Fig. 7, when the pump beam width is 0.1 mm, the maximum ΔOPD is around 23 lambdas and 45 lambdas for single-end and double-end pumping, respectively. However, inside the ±0.05 mm pump region, ΔOPD is negligible.

Figure 8a, b shows the simulated maximum ΔOPD over the pump region for single-end and double-end Gaussian-pumped slabs, respectively. According to Fig. 8, for a pump beam width less than half the slab thickness, the ΔOPD increases with the pump beam width, reaching a maximum before decreasing slowly with increasing the pump beam width. Also, note from Fig. 8 that the peak ΔOPD value in thick slabs is lower than that in thin slabs.

Fig. 8
figure 8

Simulated maximum ΔOPD over the pump region for a single-end and b double-end Gaussian-pumped slabs. The pump power level is 1 kW for the single-end-pumped slab and 2 kW (1 kW for each end) for the double-end-pumped slab

Full size image

4 The thermal effect induced beam quality degradation

In an end-pumped slab, the seed signal beam is typically focused and injected into the slab, leading to the formation of the far-field signal beam inside the slab. According to the Fourier Optics theory, the far-field beam profile is the Fourier transform of the near-field beam pattern. Therefore, using FFT enables the near-field pattern to be computed form the far-field beam pattern (normalized), and hence, the beam quality can be computed. Figure 9 illustrates the simulation of the beam quality using FFT, where a lens placed in the near-filed plane, P1, enables the simulation of the signal beam at the focal plane, P2.

Fig. 9
figure 9

Approach for the simulation of the beam quality using FFT. A lens is placed in the near-filed plane, P1, for the simulation of the signal beam at the focal plane, P2. The signal beam widths at P1 and P2 are 2w P1 and 2w P2 , respectively

Full size image

An incident signal beam, of beam width 2wP1, passing through a focusing element placed at plane P1 is converted at the focal plane P2, to a beam of width 2wP2, with a far-field divergence angle of approximately 2wP1/f. Based on the Gaussian Beam Optics theory, the widths of the near and far signal beams are given by the following equation [21]:

$$w^{2} = 2\frac{{\int {(x - \overline{x} )^{2} I(x){\text{d}}x{\text{d}}y} }}{{\int {I(x){\text{d}}x{\text{d}}y} }},$$
(6)

where I(x) is the Gaussian beam intensity, x is the distance from the center, \(\bar{x}\), of the Gaussian beam. Typically, an ideal TEM00 Gaussian beam gets distorted as it propagates through an optical medium that comprises non-ideal optical components. The beam quality, M 2, is typically defined as [21]

$$M^{ 2} = \frac{{\left[ {\theta w} \right]_{\text{dist}} }}{{\left[ {\theta w} \right]_{{{\text{TEM}}_{00} }} }} = \frac{{\left[ {(w_{P1} / {\text{f}}) *w_{P 2} } \right]_{\text{dist}} }}{{\left[ {(w_{P1} / {\text{f}}) *w_{P 2} } \right]_{{{\text{TEM}}_{00} }} }} = \frac{{\left[ {w_{P1} w_{P 2} } \right]_{\text{dist}} }}{{\left[ {w_{P1} w_{P 2} } \right]_{{{\text{TEM}}_{00} }} }},$$
(7)

where \(\left[ {\theta w} \right]_{\text{dist}}\) and \(\left[ {\theta w} \right]_{{{\text{TEM}}_{00} }}\)are the beam divergence angles, for the distorted and incident (ideal) Gaussian beams. Note that the final expression of M 2 is independent of the focal length, f. Since it is difficult to express the thermally induced OPD analytically, the beam quality, M 2, was evaluated numerically. The simulation configuration, shown in Fig. 10, was set in order to determine the beam quality after propagation through the gain medium. For an input laser beam of flat wavefront injected into the slab, the output wavefront typically gets affected by the thermal lensing effect and other thermally induced wavefront errors. At the output aperture, a diverging lens was used to compensate the thermal lensing effect. After the compensating diverging lens, the output wavefront, shown in Fig. 10, represents the non-lensing distortion induced by the thermal effects, which can be computed using Fast Fourier Transform, as discussed earlier. The electric field of the distorted signal beam is given by

$$E_{{{\text{TEM}}_{ 0 0} , {\text{distorted}}}} = e^{{ - {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } {w^{2} }}} \right. \kern-0pt} {w^{2} }}}} e^{{ - ik\left( {{{z + x^{2} } \mathord{\left/ {\vphantom {{z + x^{2} } {2R}}} \right. \kern-0pt} {2R}}} \right) - i*\arctan \left( {{z \mathord{\left/ {\vphantom {z f}} \right. \kern-0pt} f}} \right)}} e^{{ - i2\pi \Delta {\text{OPD}}}}$$
(8)
Fig. 10
figure 10

Proof-of-concept experimental model for evaluating the non-lensing distortion induced by the thermal effects and hence the beam quality of slab gain media

Full size image

Note that Fig. 7 shows the non-lensing component of the phase distortion \(e^{{ - i2\pi \Delta {\text{OPD}}}}\) induced into the TEM00-Gaussian-mode, which was calculated, for different pumping conditions, using Eq. 8 in conjunction with Fast Fourier transformation.

Note that the beam quality, M 2, was computed for different pumping conditions and slab thicknesses. The seed signal beam typically has uniform distribution along the slow-axis direction and Gaussian profile with a width smaller than the pump beam width along the x-axis direction.

To investigate the impact of the overlap between the seed and pump beams on the slab’s gain, the ratio of the Gaussian seed laser radius to the pump beam radius was set at 0.4, which is close to a practical value. Figure 11a–f shows the simulated beam quality factor, M 2, for different pump power levels and slab thicknesses. Comparing Figs. 11 and 8, it is obvious that the trend of the computed M 2 factor is similar to the trend of ΔOPD over the pump region; hence, the ΔOPD trend can be used for beam quality assessment. It is noted from Fig. 11 that increasing the pump power increases the M 2 factor, and increasing the slab thickness improves the beam quality. This is because when the pulse repetition rate is low and pump power is high, the temperature distribution is almost independent from pulse to pulse. Also, note from Fig. 11 that for thick slabs, the temperature distribution at the sides of the pump beam becomes smoother after several pulses in comparison with the temperature distribution in thin slabs, making the OPD effect similar to thermal lensing, resulting in less ΔOPD, and hence, an improved output beam quality.

Fig. 11
figure 11

Simulated beam quality as a function of the pump beam width for single-end and double-end pumping with different pump power levels, and for different slab thicknesses

Full size image

Note also that for a slab thickness of 1 mm, the maximum value of M 2 factor occurs for a pump beam width of 0.9 mm, which does not correspond to the 0.4-mm beam width at which ΔOPD is maximum. The reason is that although the peak ΔOPD value is almost the same for pump beam widths between 0.6 mm and 0.9 mm, the region affected by a large OPD is larger, making its overall effect for the pump beam width 0.9 mm more significant than that for the 0.6 mm pump beam width.

5 Conclusion

In this paper, the transient thermal distribution and thermally induced beam quality (M 2) degradation in low repetition (10 Hz) and hundred-mJ-level end-pumped Yb:YAG slab amplifiers with different thicknesses are numerically simulated and discussed. Both single- and double-end pumped amplifiers are considered. Simulation results have shown that under the same pump power and cooling condition, thicker slabs exhibit smaller OPD, and that the OPD curve shapes are almost independent of the slab thickness; however, for double-end-pumping, the OPD is approximately twice that the OPD of single-end-pumped slabs. Results have also shown that the thermally induced OPD affects the laser performance through two key phenomena, namely (1) the thermal lensing effect, and (2) the non-lensing-based wavefront distortion, which degrades the beam quality. Moreover, simulation results have revealed that most of the non-lensing-based wavefront distortion is concentrated near the boundaries of the slab, and that, for given pump power and slab thickness, the ΔOPD over the pump region increases first with increasing the pump beam width and reaches a maximum value beyond which the ΔOPD decreases at a lower rate. Furthermore, the impact of thermal lensing and other thermal effects on the output beam quality has been simulated using Fast Fourier Transformation (FFT), and the results reveal that the ΔOPD trend can be used for beam quality assessment.

Additionally, simulation results have shown that the thermally induced effects in single- and double-end pumped Yb:YAG slabs operating at low repetition rates and high power pump levels, could, in some cases, smooth the thermal distribution over the slab thickness, leading to less beam distortion, and hence, enabling thicker slabs to generate laser beams of high quality.