A methodology for identifying thermographic phosphors suitable for high-temperature gas thermometry: application to Ce³⁺ and Pr³⁺ doped oxide hosts

Abstract

A methodology is presented that utilizes configurational coordinate diagrams in combination with energy level diagrams to select new potential thermographic phosphors for high-temperature gas thermometry applications. Oxide hosts doped with trivalent ions were investigated, and based on the analysis Ce³⁺ doped ortho-phosphates (GdPO₄, LuPO₄, YPO₄) were selected for testing. All three phosphors had high measured quenching temperatures ($T_{50} > 800\, K$), partially validating the methodology used. Additionally, the quenching temperature for Ce:GdPO₄ of $T_{50} = 1000\, K$ was more than $150\, {\text{K}}$ larger than previously seen for trivalent ions doped in oxide hosts. The encouraging results demonstrate that this analysis may be applied to aid in finding thermographic phosphors for gas thermometry at combustion relevant temperatures.

1 Introduction

Thermographic phosphors are often composed of rare-earth elements doped into crystalline host structures. Gas and surface temperature measurements using these materials have been extensively reported in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] due to their many advantageous properties. For gas thermometry applications, they are ground or formed into small particles, with diameters usually in the range of 0.1–10 μm, making them minimally intrusive when using appropriate seeding concentrations. They are generally non-reactive and, with suitable host materials, can withstand temperatures in excess of 2000 K, making them suitable for combustion environments. In practice, the phosphor particles are seeded into the flow under investigation and upon excitation by a laser source they emit temperature-dependent radiation. This emission is typically insensitive to pressure and the chemical environment, making rare-earth thermographic phosphors a promising candidate to overcome many of the shortcomings of other laser-based and conventional thermometry methods.

This work focuses on a methodology for identifying phosphor compositions that have high quantum yields at elevated temperatures for use in aerosol phosphor thermometry (APT). Applications of APT to measure gas temperature have previously been limited to temperatures less than 800 K due to decreasing signal levels with increasing temperature. The decrease in signal is a result of increasing nonradiative decay rates with increasing temperature.

Assuming a simple single exponential time decay of the laser-excited luminescence, the total signal emitted from an excited state is

$$S_{1 = } N_{{1,{\text{i}}}} A_{\text{R}} \tau .$$

(1)

In Eq. (1), $N_{\text{1,i}}$ is the initial population in the excited electronic state and $A_{\text{R}}$ is the Einstein A coefficient for spontaneous radiative emission (radiative transition probability). The lifetime $\tau$ of the emission is given by

$$\tau = (A_{\text{R}} + W_{\text{NR}} )^{ - 1}$$

(2)

where $W_{\text{NR}}$ is the total nonradiative transition probability from the excited state. Generally, the radiative transition probability ($A_{\text{R}}$) is considered to be independent of temperature. In contrast, the nonradiative transition probability ($W_{\text{NR}}$) increases rapidly with temperature and can often be described by an exponential dependence on energy gap [18]

$$W_{\text{NR}} = N_{\text{uv}} { \exp }( - E_{\text{i}} /k_{\text{B}} T) ,$$

(3)

where $E_{\text{i}}$ is the characteristic energy gap associated with a nonradiative process. The nonradiative attempt rate $N_{\text{uv}}$ is of the same order of magnitude as the characteristic phonon frequency of the host material. Above a threshold temperature, the nonradiative transition probability becomes comparable to the radiative transition probability and the emission lifetime (and signal level) begins to decrease significantly with temperature. Although this sensitivity to temperature is one of the mechanisms that makes lifetime-based phosphor thermometry possible, it has the negative consequence of leading to decreased signal level at high temperatures. At high enough temperatures, the emission is dominated by nonradiative transition rates and the phosphor emission becomes completely thermally quenched.

Two types of radiative emission characterize rare-earth thermographic phosphors. The first type, intra-configurational $4f^{N} \to 4f^{N}$ emission, has sharp spectral lines. These transitions are not dipole-allowed transitions for the free ions, and only become partially allowed in the presence of the crystal field when doped into a host material [19, 20]. As a result, they have relatively long-lived emission lifetimes (on the order of 10 μs to a few ms), making it difficult to get sufficient signal levels in high-speed flow applications, while also preserving spatial resolution. The longer typical transition wavelengths in combination with slow emission rates also make these transitions susceptible to background interference from blackbody radiation at high temperatures.

More recently, research has focused on inter-configurational $4f^{N - 1} 5d \to 4f^{N}$ emission. These transitions offer some potential advantages over $4f^{N} \to 4f^{N}$ transitions. These are spin-allowed dipole transitions, leading to short radiative lifetimes (ranging from around 20 ns to 1 μs), and the emission often occurs at shorter wavelengths, in the blue or UV spectral regions, making background emission less of an issue at high temperatures. Short radiative lifetimes are advantageous for high-temperature thermometry in high-speed flow environments where short exposure times are required to freeze flow motion. Additionally, unlike the $4f^{N}$ energy states, the $4f^{N - 1} 5d$ energy level positions are highly influenced by the crystalline field such that selection of the crystalline host material plays a significant role in phosphor performance at high temperatures. With these considerations in mind, phosphors exhibiting $4f^{N - 1} 5d \to 4f^{N}$ emission were chosen as the focus for this work.

The scope of this investigation is limited to trivalent lanthanide ions doped in oxide hosts. Divalent lanthanide ions such as Eu²⁺ [16, 17, 21] have also been used in the literature for thermometry, and may be investigated in the future. The number of possible trivalent lanthanide ions that can be used for high-temperature gas thermometry can immediately be narrowed down by referring to each ion’s energy level diagram within the $4f^{N}$ configuration [22], as well as, looking at depression values $D(3 + ,A)$ for different host materials (see Table 4). The large number of high-lying $4f^{N}$ energy levels for any rare-earth ion with more than two electrons in their $f$ orbital (i.e., $N > 2$), as well as the desire to have phosphors with $4f^{N} \to 4f^{N - 1} 5d$ transitions that can be excited at convenient wavelengths ($\lambda_{\text{abs}} > 250 \;{\text{nm}}$), limits our investigation to Ce³⁺ and Pr³⁺. Oxide hosts were chosen because they generally have very high melting points, allowing them to survive the high temperatures present in combustion applications.

First, the methodology used to select potential high-temperature thermographic phosphors is introduced. It uses the concept of a configurational coordinate diagram in combination with energy diagrams. It is based on the work of Dorenbos [18, 23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] to locate the conduction band of the host material with respect to the energy levels of the rare-earth ion dopant, and the work of Struck and Fonger [38,39,40,41] to describe the potential well shapes of the $4f^{N - 1} 5d$ and $4f^{N}$ electronic levels. Previous work by the authors has shown that combining these two models allowed for successful predictions of the temperature dependence of both the emission spectra and signal level in garnet hosts doped with either Ce³⁺ or Pr³⁺ [42]. Based on this methodology, promising high-temperature phosphors are selected for testing utilizing databases presented in the literature previously by Dorenbos [24, 29, 32]. Experimental data on the selected phosphors are then presented. This includes spectral, time-resolved, and integrated signal level measurements at elevated temperatures in a tube furnace. Finally, there is a discussion of the results along with some concluding remarks.

2 Phosphor selection methodology

Many of the phenomena related to radiative emission and thermal quenching for $4f^{N - 1} 5d \to 4f^{N}$ transitions have been successfully described using configurational coordinate diagrams. Referring to Fig. 1, the probability of nonradiative transitions leading to temperature quenching can be understood considering two different pathways, and their respective energy barriers, in combination with Eq. (3). The first energy barrier, given as $E_{\text{dc}}$ in Fig. 1, represents the energy gap between the lowest $4f^{N - 1} 5d$ energy level and the conduction band. Use of this barrier assumes that fast equilibration exists among the different 5d states. This assumption is generally valid due to the high probability of an electron losing energy to lattice vibrations resulting in high equilibration rates [43]. The second energy barrier, $E_{\text{isc}}$, represents the energy gap between the bottom of the lowest $4f^{N - 1} 5d$ potential well and the intersection point between the $4f^{N - 1} 5d$ and its lower adjacent $4f^{N}$ potential wells. Determination of these characteristic energy gaps is the subject of the following sections, and the development of these relationships is discussed in detail in [42]. There exists another potential nonradiative pathway that can be characterized by an energy gap and takes place through the charge transfer state (CTS). The properties of the CTS for trivalent Europium (Eu³⁺) doped in different hosts have been investigated thoroughly in the literature [29]. For Ce³⁺ and Pr³⁺, the charge transfer (CT) energy gap is very large, often larger than the entire bandgap of the host material, making the transition probability of this mechanism negligibly small. As a result, quenching through the CTS is not considered in this analysis.

Fig. 1

Configurational coordinate energy diagram for a rare-earth ion impurity in a host material

An estimate of when the nonradiative transition rates become important can be made using the concept of the quenching temperature $T_{50}$, which is defined as the temperature at which 50% of the radiative signal has been quenched by nonradiative transitions, or equivalently when the nonradiative transition rate becomes equal to the radiative transition rate. Using Eqs. (1–3) and assuming $N_{{1,{\text{i}}}}$ is constant with temperature, the expression for $T_{50}$ is given by Eq. (4) below.

$$T_{50} = \frac{{E_{\text{i}} /k_{\text{B}} }}{{{ \ln }(N_{\text{uv}} /A_{\text{R}} )}}$$

(4)

In Eq. (4), $E_{\text{i}}$ would usually be the smallest value between $E_{\text{isc}}$ and $E_{\text{dc}}$. This expression shows that the quenching temperature should increase approximately linearly with $E_{\text{i}}$. Therefore, our task is to select a phosphor that maximizes these energy barriers to allow for luminescence emission at high temperatures.

2.1 Construction of energy diagrams to determine $E_{\text{dc}}$

The method for determining the energy gap $E_{\text{dc}}$ leverages the work of Dorenbos [18, 23,24,25,26,27,28,29,30,31,32,33,34,35,36]. We only briefly summarize the process here; full details of the method are given in [42]. First, the algebraic relationship between the band gap in host material $A$ ($E_{\text{vc}} \left( A \right)$) and the absolute energy level positions of a rare-earth ion can be derived from Fig. 1.

$$E_{\text{dc}} \left( {N,Q,A} \right) = E_{\text{vc}} \left( A \right) - E_{\text{vf}} \left( {N,Q,A} \right) - E_{{{\text{zp}},fd1}} \left( {N,Q,A} \right)$$

(5)

In Eq. (5), $E_{\text{vf}} \left( {N,Q,A} \right)$ is the energy gap between the valence band and the ground state $4f^{N}$ energy level of the rare-earth ion having $N$ $4f$ electrons and net charge $Q$ and $E_{{{\text{zp}},fd1}} \left( {N,Q,A} \right)$ is the zero-phonon energy between the $4f^{N}$ and $4f^{N - 1} 5d$ potential wells. In previous work [42], the following expression for $E_{\text{dc}} \left( {N,3 + ,A} \right)$ for trivalent ions was developed

$$\begin{aligned} E_{\text{dc}} \left( {N,3 + ,A} \right) = 1.08 \times E_{\text{ex}} \left( A \right) - E^{\text{CT}} \left( {6,3 + ,A} \right) - \Delta E_{\text{vf}} \left( {N,6,3 + } \right) + U(6,A) \hfill \\ - E_{fd1} \left( {N,3 + ,{\text{free}}} \right) + D\left( {3 + ,A} \right) + \frac{{S\left( {3 + ,A} \right)}}{{1 + k_{\text{r}} \left( {N,3 + ,A} \right)}} . \hfill \\ \end{aligned}$$

(6)

All the parameters on the right-hand side of Eq. (6) have been determined based on data tabulated for hundreds of different host materials [24, 29, 32]. The first term on the right-hand side is equal to the bandgap, i.e., $E_{\text{vc}} \left( A \right) = 1.08 \times E_{\text{ex}} (A)$. It has been previously correlated to the more easily measurable exciton energy $E_{\text{ex}} (A)$, which has been tabulated for many host materials in work performed by Dorenbos [29].

The next three terms equal $E_{\text{vf}} \left( {N,3 + ,A} \right)$. Dorenbos has shown that the energy gap between the valence band and ground state $4f^{N}$ level $E_{\text{vf}} \left( {N + 1,2 + ,A} \right)$ for a divalent rare-earth element is approximately equal to the charge transfer energy of the element’s trivalent counterpart $E^{\text{CT}} (N,3 + ,A)$ [28]. The charge transfer energy $E^{\text{CT}} (6,3 + ,A)$ for trivalent Eu³⁺ has been tabulated for many different hosts [29]. The analysis was extended to trivalent ions by introducing the coulomb correlation energy $U(6,A)$, defined as the binding energy difference between an electron in the Eu²⁺ $4f^{7}$ ground state and an electron in the Eu³⁺ $4f^{6}$ ground state [30,31,32,33, 35, 36]. Using these relationships, $E_{\text{vf}} \left( {N,3 + ,A} \right)$ is found using the relationship $E_{\text{vf}} \left( {N,3 + ,A} \right) \approx E^{\text{CT}} \left( {6,3 + ,A} \right) - U\left( {6,A} \right) + \Delta E_{\text{vf}} \left( {N,6,3 + } \right)$ [28, 30], where $\Delta E_{\text{vf}} \left( {N,6,3 + } \right)$ is defined as the energy difference between the lowest $4f^{N}$ level with respect to the valence band of any trivalent ion and that of Eu³⁺, which has been found previously for each trivalent rare-earth element [31].

The coulomb correlation energy $U(6,A)$ was shown empirically to be correlated well with the Ce³⁺ $5d$ centroid shift [35]. As a result, the Ce³⁺ $5d$ centroid shift and the coulomb correlation energy ($U\left( {6,A} \right)$) have been tabulated for 150 different compounds [32]. Another method to determine $U\left( {6,A} \right)$ involves using photoconductivity measurements of Ce³⁺ ($E_{\text{pc}} \left( {1,3 + ,A} \right)$) to locate the conduction band of the host material with respect to the ground $4f^{1}$ state. It was shown previously [42] that $E_{\text{pc}} \left( {1,3 + ,A} \right)$ can be related to $U\left( {6,A} \right)$ by

$$U\left( {6,A} \right) = E_{\text{pc}} \left( {1,3 + ,A} \right) + E^{\text{CT}} \left( {6,3 + ,A} \right) + \Delta E_{\text{vf}} \left( {1,6,3 + } \right) - 1.08 \times E_{\text{ex}} \left( A \right) .$$

(7)

In this paper, wherever data from photoconductivity measurements could be found, they were used to calculate $U(6,A)$, and Eq. (6) was used to estimate $E_{\text{dc}} \left( {N,3 + ,A} \right)$. If photoconductivity measurements were not available, the value of $U(6,A)$ used was taken from tabulated data [32].

The final three terms on the right side of Eq. (6) equal $E_{{{\text{zp}},fd1}} \left( {N,3 + ,A} \right)$, shown previously [42] to be related to the $4f^{N} \to 4f^{N - 1} 5d$ peak absorption energy $E_{fd1} \left( {N,3 + ,A} \right)$ through the relationship $E_{{{\text{zp}},fd1}} \left( {N,3 + ,A} \right) = E_{fd1} \left( {N,3 + ,A} \right) - S\left( {3 + ,A} \right)/(1 + k_{\text{r}} \left( {N,3 + ,A} \right)),$ where $k_{r} (N,3 + ,A) = k_{f} /k_{d}$ is the ratio between the parabola stiffness of the lower and upper electronic levels and $S\left( {3 + ,A} \right)$ is the Stokes shift, values for which have been found for hundreds of host materials [24]. The value of $E_{fd1} \left( {N,3 + ,A} \right)$ is able to be determined from the relationship $E_{fd1} \left( {N,3 + ,A} \right) = E_{fd1} \left( {N,3 + ,{\text{free}}} \right) - D(3 + ,A)$ [24], where $E_{fd1} \left( {N,3 + ,{\text{free}}} \right)$ is the energy for the first $4f^{N} \to 4f^{N - 1} 5d$ transition in a free ion, and is known for all of the divalent and trivalent lanthanide series [23, 28]. Values of the depression ($D(3 + ,A)$) have been compiled for several hundred host materials in the literature [24]. The value of $k_{\text{r}} (N,3 + ,A)$ is the only remaining unknown parameter. The method used to estimate this parameter will be discussed in Sect. 2.3.

2.2 Using the configurational coordinate diagram to estimate $E_{\text{isc}}$

The other thermal quenching mechanism considered originates in part due to the relative displacement $a$ between the equilibrium positions of the $4f^{N - 1} 5d$ and $4f^{N}$ configurations shown in Fig. 1. The shifted potential well leads to nonradiative transitions between the $4f^{N - 1} 5d$ and $4f^{N}$ states through a thermally activated intersystem crossing. An expression for the characteristic energy gap $E_{\text{isc}} (N,3 + ,A)$ (assuming $k_{\text{r}} \left( {N,3 + ,A} \right) > 1$) for this process was derived previously [42].

$$E_{\text{isc}} \left( {N,3 + ,A} \right) = \left[ {\frac{{k_{\text{r}} \left( {N,3 + ,A} \right)\sqrt {\frac{{S\left( {3 + ,A} \right)}}{{1 + k_{\text{r}} \left( {N,3 + ,A} \right)}}} - \sqrt {\frac{{S\left( {3 + ,A} \right)}}{{1 + k_{\text{r}} \left( {N,3 + ,A} \right)}} + \left( {k_{\text{r}} \left( {N,3 + ,A} \right) - 1} \right)E_{\text{gap}} \left( {N,3 + ,A} \right)} }}{{1 - k_{\text{r}} \left( {N,3 + ,A} \right)}}} \right]^{2}$$

(8)

Many of the uncertainties and simplifications leading to potential inaccuracies in Eq. (8) have been discussed [42]. The hope is for Eq. (8) to be a useful guide to understanding how the probability of this nonradiative mechanism roughly depends on specific parameters. It was shown previously that this expression explained temperature quenching data well for Pr³⁺ ions doped in garnet hosts [42].

As can be seen in Eq. (8), $E_{isc} (N,3 + ,A)$ for a given ion-host combination is a function of three parameters.

• 1. The Stokes shift $S(3 + ,A)$. This parameter has been tabulated for hundreds of host materials [24].

• 2. The energy gap between the $4f^{N - 1} 5d$ absorption energy and the highest energy level in the $4f^{N}$ configuration $E_{\text{gap}} \left( {N,3 + ,A} \right) = E_{fd1} \left( {N,3 + ,A} \right) - E_{4f} \left( {N,3 + } \right).$ Again, $E_{fd1} \left( {N,3 + ,A} \right)$ for many host materials is known from depression values tabulated by Dorenbos [24]. The term $E_{4f} \left( {N,3 + } \right)$ is the energy spacing between the ground state $4f^{N}$ level and the upper $4f^{N}$ level that lies directly below the lowest $4f^{N - 1} 5d$ state, as shown in Fig. 1. It is also known for all $4f^{N}$ ions, and is considered approximately invariant to the host material due to the shielding of the inner $4f^{N}$ orbitals [31]. For Ce³⁺ a value of $E_{4f} \left( {1,3 + } \right) = 2000\; {\text{cm}}^{ - 1}$ is used and for Pr³⁺, $E_{4f} \left( {2,3 + } \right) = 22268\; {\text{cm}}^{ - 1}$ was used based on measurements of the ${}_{{}}^{3} P_{2}$ energy in Pr:YAG [44].

• 3. The ratio of the stiffness of the $4f^{N}$ and $4f^{N - 1} 5d$ potential wells $k_{\text{r}} \left( {N,3 + ,A} \right) = k_{f} /k_{d}$ also appears in Eq. (6). This value is the only unknown parameter, and has been estimated previously for Pr:YAG, Ce:YAG, Pr:LuAG and Ce:LuAG using a quantum mechanical single configurational coordinate (QMSCC) model to describe each phosphors’ temperature-dependent emission spectrum. Its determination is discussed next.

2.3 Using the quantum mechanical single configurational coordinate (QMSCC) model to determine $k_{\text{r}} \left( {N,3 + ,A} \right)$

The QMSCC model was first developed by Struck and Fonger [40], and has been used in the literature to explain the temperature dependence of radiative and nonradiative transitions between an excited state and its lower states [39,40,41, 45, 46]. Referring to Fig. 1, a $4f^{N - 1} 5d$ energy level in parabola $d$ is defined by quantum number $m$, wave function $d_{m}$, phonon energy $\hbar \omega_{d}$ and parabola stiffness $k_{d}$. Analogously, a $4f^{N}$ energy level in parabola $f$ is defined by quantum number n, wave function $f_{n}$, phonon energy $\hbar \omega_{f}$ and parabola stiffness $k_{f}$. The total radiative transition $R_{\text{DF}}$ rate is given by Eq. (9).

$$R_{\text{DF}} = R_{\text{df}} \mathop \sum \limits_{{p_{U} = - \infty }}^{\infty } U_{{p_{U} }}$$

(9)

$$U_{{p_{U} }} = \mathop \sum \limits_{{m = m_{0} }}^{\infty } (1 - r_{d} )r_{d}^{m} \left[ {F_{m} \langle f_{{p_{U} + i_{m} - 1}} |d_{m}\rangle^{2} + (1 - F_{m} )\langle f_{{p_{U} + i_{m} }} |d_{m}\rangle^{2} } \right]$$

(10)

In Eq. (9), $R_{\text{df}}$ is a constant from the electronic portion of the overlap integral ($R_{\text{df}} \approx 10^{7} {\text{s}}^{ - 1}$ for allowed radiative transitions).

The distribution $U_{{p_{U} }}$ in Eq. (10) gives the normalized temperature-dependent shape of the emission spectrum. In this expression, the Boltzmann factor between initial vibrational states is $r_{d} = { \exp }( - \hbar \omega_{d} /k_{\text{B}} T)$ and the Franck–Condon (FC) factors are $\langle{f_{n} |d_{m}}\rangle^{2}$. The value $i_{m}$ is the smallest integer greater than $(\hbar \omega_{d} /\hbar \omega_{f} )m$ and $F_{m} = i_{m} - (\hbar \omega_{d} /\hbar \omega_{f} )m$. The summing of quantum number $m$ in Eq. (10) starts with $m_{0} = 0$ for $p_{U} \ge 0$. For $p_{U} < 0$, $m_{0}$ is the smallest index for $p_{U} + i_{m} = 0$. For further details on the summation rules in Eq. (10), refer to previous work by Struck and Fonger [40, 41]. As will be seen later in this paper, fitting this $U_{{p_{U} }}$ distribution to temperature-dependent emission spectra measurements allows the determination of key parameters, such as characteristic phonon energies and the parabola stiffness ratio $k_{\text{r}} \left( {N,3 + ,A} \right)$.

The quantum number $p_{U}$ is defined as $p_{U} = n - (\hbar \omega_{d} /\hbar \omega_{f} )m$. Referring again to Fig. 1, the radiative energy balance is

$$E_{{{\text{zp}},fd1}} - p_{U} \hbar \omega_{f} - h\nu_{{p_{U} }} = 0.$$

(11)

The photon energy from the radiative transition is $h\nu_{{p_{U} }}$. This photon can bridge any energy gap. As a result, all values of $p_{U} = 0, \pm 1, \pm 2, \ldots$ can be summed over and thus $\sum\nolimits_{{p_{U} = - \infty }}^{\infty } {U_{{p_{U} }} } = 1$. This leads to a total radiative transition rate that is constant with temperature, $R_{\text{DF}} = R_{\text{df}}$.

The overlap integrals $\langle{f_{n} |d_{m}}\rangle$ in Eq. (10) can be solved using the Manneback recursion formulas [40], given by Eq. (12).

$$A_{0,0} = (\sin 2\theta )^{1/2} { \exp }\left( - \frac{1}{8}\left( {\sin 2\theta } \right)^{2} a_{fd}^{2} \right)$$

(12)

$$(m + 1)^{1/2} A_{n,m + 1} = - \left( {\cos 2\theta } \right)m^{{\frac{1}{2}}} A_{n,m - 1} - \left( {\sin 2\theta } \right)2^{{ - \frac{1}{2}}} a_{fd} (\cos \theta )A_{n,m} + \left( {\sin 2\theta } \right)n^{{\frac{1}{2}}} A_{n - 1,m}$$

$$(n + 1)^{1/2} A_{n + 1,m} = \left( {\cos 2\theta } \right)n^{{\frac{1}{2}}} A_{n - 1,m} + \left( {\sin 2\theta } \right)2^{{ - \frac{1}{2}}} a_{fd} (\sin \theta )A_{n,m} + \left( {\sin 2\theta } \right)m^{{\frac{1}{2}}} A_{n,m - 1}$$

In Eq. (12), $A_{n,m}$ represents the overlap integral $\langle{f_{n} |d_{m}}\rangle$. These relations depend on two parameters. The first, referred to as the Manneback angle $\theta$, is a function of the ratio of the parabola force constants $k_{\text{r}} (N,3 + ,A)$ [38].

$$\tan \theta = \left(\frac{{k_{d} }}{{k_{f} }}\right)^{1/4} = (k_{\text{r}} (N,Q,A))^{ - 1/4} = \left(\frac{{\omega_{d} }}{{\omega_{f} }}\right)^{1/2}$$

(13)

The second parameter is a dimensionless FC offset parameter $a_{fd}$ [38]. An algebraic expression for $a_{fd}$ [42] showed that it explicitly depends only on the stiffness ratio $k_{\text{r}}$, the phonon energy $\hbar \omega_{f}$ and the Stokes shift $S(Q,A)$.

$$a_{fd} = \sqrt {\frac{2 \cdot S(Q,A)}{{\hbar \omega_{f} }}} \sqrt {\frac{{k_{\text{r}}^{ - 1/2} + 1}}{{k_{\text{r}}^{ - 1} + 1}}}$$

(14)

For a spectra consisting of multiple electronic transitions, the final step to constructing the emission spectrum involves knowledge of the relative transition intensities, or the branching ratios, between the upper electronic level being studied and all other lower electronic levels. The branching ratio $\beta_{\text{i}}$ is defined below.

$$\beta_{\text{i}} = A_{\text{i}} /A_{\text{R}}$$

(15)

In Eq. (15) $A_{\text{i}}$ is the transition probability between the upper $4f^{N - 1} 5d$ electronic level and a lower $4f^{N}$ electronic level with energy $E_{4f,i} (N,Q)$. Summing over all lower electronic levels gives the total radiative transition probability of that upper electronic level, such that $\sum\nolimits_{i} {A_{i} } = A_{\text{R}}$ and thus $\sum\nolimits_{i} {\beta_{i} } = 1$.

The modeling inputs controlling the shape and temperature-dependent broadening of an electronic transition in the emission spectrum are thus the stiffness ratio $k_{r} (N,3 + ,A)$, phonon energy $\hbar \omega_{f}$, and the Stokes shift $S\left( {Q,A} \right)$. The value of the absorption energy $E_{fd1} \left( {N,3 + ,A} \right)$ (or analogously the depression $D(3 + A)$) is varied to match the location of the first peak in the emission spectrum between the model and the experimental data. When multiple transitions are present in the emission spectrum, $E_{4f,i} \left( {N,Q} \right)$ is also varied to match the position of the other peaks. Finally, the branching ratios $\beta_{\text{i}}$ are varied to match the relative heights of the peaks in the emission spectrum.

Often, the values of $E_{4f,i} \left( {N,Q} \right)$, $E_{fd1} (N,Q,A)$ and $S\left( {Q,A} \right)$ can be found in the literature or obtained from low temperature spectral measurements, limiting the required number of freely varying parameters in the model. Previous modeling efforts [42] have held $E_{4f,i} \left( {N,Q} \right)$ and the Stokes shift $S\left( {Q,A} \right)$ constant, and allowed $E_{fd1} (N,Q,A)$ to vary to ensure that the modeled emission peaks matched the data. A previous paper [47] has shown that using the tabulated values of $E_{fd1} (N,Q,A)$ [24] can easily result in errors on the order of 0.1 eV, leading to a shift in the emission peak on the order of 10 nm. Therefore, in the absence of high-resolution spectral data on the absorption and emission spectrum of a phosphor, letting $E_{fd1} (N,Q,A)$ vary is likely a more suitable method to extract reliable values from the QMSCC fit. In contrast, due to the shielded nature of the inner $4f^{N}$ orbitals, the value of $E_{4f,i} \left( {N,Q} \right)$ is approximately invariant to the host material and can be safely approximated with its free ion values if chosen to do so. For example, QMSCC modeling of the emission spectra of a Ce:LuPO₄ phosphor is presented later in this paper. In this case, we allowed the value $E_{{4f,\varvec{i}}}$ of the ${}_{{}}^{2} F_{7/2}$ level to vary. The value extracted from the fit was 0.258 eV (see Table 5), corresponding to approximately a 0.01 eV difference between the usually assumed free ion value of 0.248 eV (i.e., 2000 cm⁻¹). The effect of using either value of $E_{{4f,\varvec{i}}}$ for the spectral modeling was found to be negligible in terms of the extracted parameters.

This analysis was previously shown to accurately capture both the spectral temperature-dependence and the thermal quenching behavior of Pr³⁺ and Ce³⁺ in yttrium aluminum garnet (YAG) and lutetium aluminum garnet (LuAG) host materials [42]. Table 1 shows the values of $k_{\text{r}} (N,3 + ,A)$ and $\hbar \omega_{f}$ extracted for each phosphor from that work. A more in-depth discussion of the results and experiments can be found in previous work [42]. Using the results of the QMSCC modeling from Table 1, we chose to use the values of $k_{\text{r}} \left( {Ce^{3 + } } \right) = 1.32$ and $k_{\text{r}} \left( {Pr^{3 + } } \right) = 1.57$ for the rest of this analysis. As more experimental data become available, it is hoped that more accurate and reliable predictions of these values as a function of host material and rare earth ion will become available.

Table 1 QMSCC parameters used for spectral data from [42]

2.4 Using databases from Dorenbos to select promising high-temperature phosphors

The oxide hosts considered for potential high-temperature thermographic phosphors are listed in Table 3. Overall, 58 ion-host combinations were evaluated. Table 2 shows the host-independent values for Ce³⁺ and Pr³⁺ that were used to calculate $E_{\text{dc}} (N,3 + ,A)$ and $E_{\text{isc}} (N,3 + ,A)$. All parameters were taken from Dorenbos [31] except for $k_{\text{r}} (N,3 + )$.

Table 2 Host-independent energy values in eV for Ce³⁺ and Pr³⁺

Table 3 gives the host-dependent values that were used to select promising high-temperature phosphors. All values for the depression $D(3 + A)$ and Stokes shift $S(3 + A)$ were found in the literature from [24] and values of the exciton energy $E_{\text{ex}} (A)$ and charge transfer energy $E^{\text{CT}} (6,3 + ,A)$ were taken from [29], except for the garnet family data, where depression and Stokes shift values were found in [48, 49] and exciton and charge transfer energies were taken from [33, 49]. For the coulomb correlation energy $U(6,A)$, all values in normal font were taken from [32]. The values in parenthesis were estimated based on data from [32] for host structures from the same family.

Table 3 Host-dependent parameters in eV for energy diagram and intersystem crossing calculations

Previous work from Dorenbos [30] has shown that the absolute $4f^{N}$ electron binding energy $E_{4f} (N,Q,A)$ is only a function of $U(6,A)$. Additional work then showed that $E_{4f} (N,Q,A)$ is approximately constant within a given family of host structures (i.e., REPO₄, REAlO₃, REBO₃, etc., RE = La, Gd, Y, Lu, Sc) within around $\pm 0.1 \;{\text{eV}}$ [33, 36]. As a result, we chose to assign $U\left( {6,{\text{REP}}_{3} {\text{O}}_{9} } \right) = 7.24\; {\text{eV}}$ based on data given for LaP₃O₉ in [32]. Similarly for GdPO₄, the value of $U\left( {6,{\text{GdPO}}_{4} } \right) = 7.14 \;{\text{eV}}$ was used as an estimate based on the average of LaPO₄ and YPO₄. The value of $U\left( {6,{\text{Lu}}_{2} {\text{Si}}_{2} {\text{O}}_{7} } \right) = 7.41\; {\text{eV}}$ was estimated based on emission data and energy diagrams for this host published previously [37]. This value is $0.41 \;{\text{eV}}$ larger than the tabulated value based on the 5d-centroid shift data [32]. For REAlO₃ (RE = Gd, Y), photoconductivity measurements of Ce:GdAlO₃ located the lowest $5d$ level $0.34\; {\text{eV}}$ below the conduction band [50]. This leads to a value, using Eq. (6) along with parameters from Tables 2 and 3, of $U\left( {6,{\text{REAlO}}_{3} } \right) = 6.24 \;{\text{eV}}$, which is approximately $0.5 \;{\text{eV}}$ smaller than the tabulated data [32]. Finally, photoconductivity measurements on Ce:YAG previously yielded a value of $E_{\text{pc}} \left( {1,3 + ,{\text{YAG}}} \right) = 3.8\; {\text{eV}}$ [51]. This leads to a value of $U\left( {6,{\text{RE}}_{3} {\text{Al}}_{5} {\text{O}}_{12} } \right) = 6.79\; {\text{eV}}$, which is in agreement with the tabulated value [32].

The values of the energy gaps $E_{\text{dc}} (N,3 + ,A)$ and $E_{\text{isc}} (N,3 + ,A)$ for Ce³⁺ and Pr³⁺ were estimated for these host materials, using Eqs. (6) and (8), respectively. Table 4 shows the results of the calculations. The excitation wavelength $\lambda_{\text{abs}}$ is also included in Table 4 for each phosphor. Whenever $\lambda_{\text{abs}} (Pr^{3 + } )$ was less than 215 nm, $E_{\text{isc}} \left( {Pr^{3 + } } \right)$ is not given in Table 4 because the ${}_{{}}^{1} S_{0}$ energy level is considered to lie below the $4f5d$ level, leading to an absence of $4f^{N - 1} 5d \to 4f^{N}$ emission in these phosphors.

Table 4 Calculated temperature quenching parameters for Ce³⁺ and Pr³⁺ in oxide hosts

Referring to Table 4, it is noted that the value of $E_{\text{dc}} \left( {Ce^{3 + } ,A} \right)$ is much smaller than that of $E_{\text{isc}} \left( {Ce^{3 + } ,A} \right)$ for every host considered. This is not a surprising result due to the large energy gap between the highest $4f^{1}$ level and the lowest $5d^{1}$ level in Ce³⁺. Thus, we can conclude that generally temperature quenching in hosts doped with Ce³⁺ will occur as a result of ionization to the conduction band. Conversely, the values of $E_{\text{dc}} \left( {Pr^{3 + } ,A} \right)$ and $E_{\text{isc}} \left( {Pr^{3 + } ,A} \right)$ are much more comparable due to the high-lying upper $4f^{2}$ ${}_{{}}^{3} P_{2}$ level (22,268 cm⁻¹). Therefore, either ionization to the conduction band or intersystem crossing may be responsible for temperature quenching in Pr³⁺ based phosphors, and intersystem crossing will be the dominant mechanism for hosts with large depressions. This was seen previously for the garnet family [42]. Finally, we are looking for a thermographic phosphor that can be excited at convenient wavelengths ($\lambda_{\text{abs}} > 250\; {\text{nm}}$). Too low of an excitation wavelength can lead to unwanted effects, such as signal interferences from excitation and fluorescence of different molecules, as well as, issues with laser absorption in optics at short wavelengths. Referring again to Table 4, this eliminates almost all Pr³⁺-based phosphors except for ones with large depressions, in which case the intersystem crossing energy gap becomes too small to be feasible for high-temperature applications. Based on these considerations, the ortho-phosphate group, GdPO₄, YPO₄, and LuPO₄, doped with Ce³⁺ were chosen for further investigation, since they had the largest $5d^{1}$ to conduction band energy gaps of all oxide hosts considered.

3 Experimental setup

Temperature-dependent emission measurements were performed for three different thermographic phosphor particles from the ortho-phosphate (REPO₄) family. All phosphors were purchased from Phosphor Technology Ltd:

• 1. Ce³⁺ doped into gadolinium phosphate (GdPO₄) at 0.5% (Ce:GdPO₄)

• 2. Ce³⁺ doped into yttrium phosphate (YPO₄) at 0.5% (Ce:YPO₄)

• 3. Ce³⁺ doped into lutetium phosphate (LuPO₄) at 0.5% and 0.05% (Ce:LuPO₄)

Each phosphor has their lowest $4f^{1} \to 5d^{1}$ transition centered around 300–320 nm, with their second excitation band centered around approximately 250 nm [32]. This second transition is accessible with the 266 nm 4th harmonic of an Nd:YAG laser. It has been discussed previously that the Ce:REPO₄ family is characterized by large gaps between their lowest $5d^{1}$ state and conduction band [36], but very few temperature-dependent measurements on the quenching behavior of these phosphors have been reported. One study on Ce:YPO₄ was conducted, with temperature data reported up to 700 K [52]. No thermal quenching was observed and the $T_{50}$ was estimated to be above 970 K.

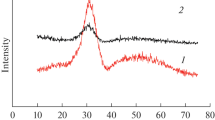
The relatively high doping concentration of 0.5% led to some interesting behavior in the phosphors’ emission spectrum. As a result, Ce:LuPO₄ was also tested at a lower doping concentration of 0.05% to investigate this effect. X-ray diffraction measurements for each phosphor are shown in Fig. 2. The diffraction patterns are in good agreement with a measurement database that includes these phosphors [53], although the higher doping concentrations in LuPO₄ and YPO₄ (Fig. 2a, d) had some additional diffraction lines compared to the database. Referring to Fig. 2a, b, the effect of a higher doping concentration on the phosphors can be observed. The 0.5% Ce³⁺ doping case shows several extra diffraction lines, likely due to additional crystalline phases or impurities, whereas the 0.05% Ce:LuPO₄ diffraction pattern is in precise agreement with the database [53]. This effect was not seen for 0.5% Ce:GdPO₄ (Fig. 2c). Its diffraction pattern is in very good agreement with the database [53], and no extra diffraction patterns were observed.

Fig. 2

X-ray diffraction measurements for: a Ce:LuPO₄ (0.5%), b Ce:LuPO₄ (0.05%), c Ce:GdPO₄ (0.5%), d Ce:YPO₄ (0.5%)

Each phosphor powder was placed in a small alumina (>99.6% purity) dish and angled upward so that the contents of it could be imaged. It was then heated in a tube furnace (CM Furnaces, Rapid Temp Model 1720-12) with a 0.305-m heated length centered in a 0.914-m long working tube used to improve temperature uniformity. The furnace is specified to have temperature uniformity of ±2 K for the central 100 mm of the hot zone. Laser excitation was provided by the 4th harmonic of a flashlamp-pumped Nd:YAG laser (Ekspla, NL 303D-10), operating at 10 Hz. The beam was approximately 4 mm in diameter and the laser energy was held at 500 µJ/pulse throughout the entire experiment.

The luminescence emission spectra were collected using a 300-mm focal length imaging spectrograph (Princeton Instruments, SP300i), outfitted with a 1024 × 1024 PI-MAX4 intensified charge couple device (ICCD) camera (gen. III HBf photocathode with P46 phosphor). Prior to each experiment, a calibration was performed with a mercury lamp to determine the spectrometer’s correct offset, linear adjustment, and dispersion parameter values. Details of the calibration procedure can be found in the software’s user manual (WinSpec/32 Manual, Version 2.5.K). A relative spectral response (RSR) correction was also applied to the data to account for the changing collection efficiency of the setup at different emission wavelengths. The RSR was performed using a quartz tungsten halogen (QTH) lamp. An integration duration of 160 ns was used for data collection, with the camera gate beginning 60 ns prior to the laser pulse. Phosphor emission was focused into a fused silica fiber bundle with a 100-mm focal length 50.8-mm diameter UV spherical lens. The 266 nm scattered laser light was rejected using two WG280 (Schott glass filter, 3 mm thickness) 280 nm longpass filters. Each measurement represents an average of 200 samples.

Time-resolved measurements of Ce:LuPO₄ (0.05%) were collected by a photodiode with a 1-ns rise time (DET 210, Thorlabs). The rise time limitation along with the laser pulse width prevented measurements at the highest temperatures, where emission lifetimes became less than 3–4 ns due to increasing nonradiative transition rates. The current capabilities were sufficient to capture the lifetime temperature sensitivity, which was the purpose of this work. The emission was focused on to the photodiode with a 100-mm focal length 50.8-mm diameter UV spherical lens. Two WG280 filters (Schott glass) and one WG295 filter (Schott glass) were used to reject 266-nm scattered laser light (<1E−6 transmission). Each measurement reported was averaged over 200 samples on an oscilloscope (Tektronix TDS 620).

4 Results and discussion

4.1 Temperature sensitivity of Ce:REPO₄ phosphors

Figure 3a, b shows the Ce:LuPO₄ spectral temperature sensitivity data for Ce³⁺ doping concentrations of 0.5% (A) and 0.05% (B). Both concentrations are characterized by broadband $4f^{N - 1} 5d \to 4f^{N}$ emission with peaks at 335 nm and 359 nm. The position of the emission peaks is in good agreement with the literature [54, 55]. Figure 3a demonstrates that the higher doping concentration leads to different temperature dependence than the 0.05% case in Fig. 3b. The most probable reasons for the discrepancy are reabsorption as well as emission from defects and other crystalline phases that are present in the higher doping concentration sample. In both Fig. 3a, b, it is seen that at 300 K there also seems to be some anomalous emission near 320 nm, but at higher temperatures it has been substantially quenched, and the temperature-dependent broadening becomes similar to what would be expected.

Fig. 3

Emission spectrum as a function of temperature for: a Ce:LuPO₄ (0.5%), b Ce:LuPO₄ (0.05%), c Ce:GdPO₄ (0.5%), d Ce:YPO₄ (0.5%)

Figure 3c, d displays the spectral temperature dependencies of Ce:GdPO₄ and Ce:YPO₄, respectively. The Ce:GdPO₄ (Fig. 3c) emission is characterized at room temperature by emission peaks at 321 and 340 nm, in good agreement with literature [53, 56]. As the temperature increases, the emission spectra broaden and the two peaks are no longer observable due to increasing population of higher vibrational levels.

The emission peaks at 335 nm and 355 nm in Ce:YPO₄ (Fig. 3d) are also in agreement with the literature [52, 53, 56,57,58], although the general shape of the emission spectrum looks different. Emission around 320 nm is seen, and seems to be decreasing relative to the rest of the spectrum as a function of temperature. This gives the appearance of a narrowing of the lower wavelength band as a function of temperature. Additionally, the two peaks are not as easily discernable as usually observed [52, 53, 56,57,58]. Similar to the 0.5% Ce:LuPO₄ case in Fig. 3a, probable reasons for this behavior include emission from defects as well as the presence of additional crystalline phases impacting the emission spectrum. The X-ray diffraction pattern in Fig. 2d provides some supporting evidence for this conclusion.

QMSCC modeling of Ce:LuPO₄ with 0.05% doping starting at 500 K performed to extract the required parameters to construct its configurational coordinate diagram. The Stokes shift $S(Q,A)$ used in the modeling was taken from Table 3 and held constant. The values of $k_{\text{r}} (n,Q,A)$, $\hbar \omega_{f}$, and the branching ratios $\beta_{i}$ were used as fitting parameters to fit the shape and temperature dependence of the modeled emission spectrum to the data. $E_{fd1}$ (i.e., $D(3 + )$) and $E_{4f}$ were adjusted to match the positions of the modeled emission peaks to the data. A multivariate fit was performed on the spectral temperature data using Igor Pro 7 (Wavemetrics). The parameters extracted from the fit are shown in Table 5, and the results are shown in Fig. 4a.

Table 5 QMSCC parameters used for Ce:LuPO₄

Fig. 4

Spectral data (solid lines) compared with QMSCC results (dotted lines) (a) and configuration coordinate diagram (b) for Ce:LuPO₄

Good agreement between the data and modeled spectral temperature dependence was able to be achieved. The value of $k_{\text{r}} = 1.12$ determined from the fitting is smaller than in previous modeling of Ce³⁺ in Garnet-based phosphors [42]. The phonon energy $\hbar \omega_{f}$ of 187 cm⁻¹ is in agreement with previously reported low temperature electronic and vibronic spectra measurements for Ce:LuPO₄ [59], where phonon energies between 120 and 227 cm⁻¹ were measured. Using the results of the QMSCC model, Fig. 4b shows the estimated configurational coordinate diagram for Ce:LuPO₄. The extremely large deduced value of $E_{\text{isc}} \left( {{\text{Ce}}^{3 + } ,{\text{LuPO}}_{4} } \right) = 12.7 {\text{eV}}$ shows pictorally how this transition is extremely unlikely. In addition, this transition would have to occur inside the conduction band, in which case the electron has already been delocalized due to ionization to the conduction band. It should be noted that the value of $E_{\text{isc}}$ determined from the QMSCC modeling is more than twice as large as predicted in Table 4 by assuming a value of $k_{\text{r}} = 1.32$. The large sensitivity of $E_{\text{isc}}$ to this parameter highlights the importance of accurate $k_{\text{r}}$ estimates. This is especially the case when intersystem crossing may be the dominant quenching mechanism, as it has been shown to be previously for Pr³⁺ based phosphors [42].

No QMSCC modeling of Ce:YPO₄ or Ce:GdPO₄ was attempted. For Ce:YPO₄, this was due to the high doping concentration affecting the phosphors’ structure and emission spectrum. For Ce:GdPO₄, there is still considerable uncertainty in both the values of the depression $D(3 + ,A)$ and Stokes shift $S(3 + ,A)$ of this phosphor [36, 53, 56]. The stiffness ratio $k_{\text{r}}$ that is extracted out of the QMSCC model is quite sensitive to the value of the Stokes shift used in the modeling. As a result, it was decided not to attempt any modeling of this phosphors’ emission spectrum until these values are more precisely known.

Figure 5a shows the dependence of the signal level on temperature for the Ce:REPO₄ phosphors. An initial temperature range where nonradiative transitions are unimportant characterizes each phosphor, and thus the signal level is relatively steady. Some changes in signal level as a function of temperature for all three phosphors in this range were observed, especially for Ce:LuPO₄ (0.05%), and this was interpreted as a changing initial population $N_{{ 1 , {\text{i}}}}$ in the excited state, from Eq. (1). To confirm this, lifetime measurements of Ce:LuPO₄ (0.05%) were conducted, and the results are shown in Fig. 5b. As can be seen, the lifetime is unchanged until 800 K, when it begins to decrease rapidly. The rapid decrease in Ce:LuPO₄ signal level at temperatures greater than 800 K is also seen, confirming that the initial changes in signal level are from changes in $N_{{ 1 , {\text{i}}}}$, due to changing absorption bands and/or energy transfer between the first two $5d^{1}$ bands with increasing temperature.

Fig. 5

Signal level temperature dependence data for Ce:REPO₄ phosphors (a) and lifetime measurements for Ce:LuPO₄ (b)

After a critical temperature the nonradiative transition rates start to dominate and the signal level for each phosphor begins to decrease rapidly. The measured quenching temperature ($T_{50}$), approximated as the temperature when the signal dropped to 50% of its maximum, was 800, 935, and 1000 K for YPO₄, LuPO₄, and GdPO₄, respectively. These values are quite high, and the quenching temperatures for LuPO₄ and GdPO₄ are higher than previously seen to our knowledge. The value of $T_{{50,{\text{YPO}}_{4} }} = 800\, {\text{K}}$ is slightly lower than previous work [52], which predicted a quenching temperature greater than 970 K based on measurements up to 700 K. This may be due to the high doping concentration affecting the crystal structure and emission properties of this phosphor.

4.2 Comparison with other data in literature

In addition to the data taken for this work, temperature quenching data were gathered from the literature on some of the phosphors that were examined in Sect. 2. The list of phosphors for which data were found is shown in Table 6, along with the reference for each result. The smallest energy gap between $E_{\text{isc}}$ and $E_{\text{dc}}$, provided in Table 4, is also given in Table 6. Based on Eq. (4), a linear relation should exist between the quenching temperature $T_{50}$ and the smallest energy gap $E_{\text{i}}$. The results of a linear regression fit are plotted in Fig. 6, with the dotted lines representing 2 standard deviation prediction bands.

Table 6 Temperature quenching data for different phosphors found in the literature

Fig. 6

Quenching temperature data for several oxide phosphors plotted against their smallest predicted energy gap ($E_{\text{dc}}$ or $E_{\text{isc}}$)

As can be seen, the relationship is indeed roughly linear, although there is a significant amount of scatter in the data. Quenching temperatures can easily deviate from that predicted by 200 K. This is to be expected due to the many simplifications and assumptions made in this analysis. It has been shown previously that systematic errors arising from each step in the construction of thermographic phosphor energy diagrams can culminate in an error in the predicted value of $E_{\text{dc}}$ on the order of 0.3–0.5 eV [47]. This fact alone is enough to explain much of the scatter seen in Fig. 6. Furthermore, the assumption of a linear relationship between quenching temperature and nonradiative energy gap implies that the ratio of the electronic portion of the nonradiative and radiative overlap integrals $N_{\text{uv}} /A_{\text{R}}$ is constant. This is obviously not necessarily the case, and as a result some of the scatter may also be attributed to this assumption.

Two phosphors from Table 6, ${ \Pr }:{\text{Y}}_{3} {\text{Al}}_{1} {\text{Ga}}_{4} {\text{O}}_{12}$ and ${ \Pr }:{\text{Y}}_{3} {\text{Al}}_{2} {\text{Ga}}_{3} {\text{O}}_{12}$ were predicted to undergo temperature quenching due to intersystem crossing, when previous work [49] convincingly showed experimentally that ionization to the conduction band was the true mechanism. The reason for this error may be due to an over predicted value of $E_{\text{dc}}$ in Table 4, possibly from changing values of $U\left( {6,A} \right)$ with increasing Ga content. These phosphors are shown in bold in Table 6 and circled in Fig. 6. This discrepancy could also be due to inaccuracy in the assumed value of $k_{\text{r}}$, which, as we showed earlier can significantly impact the predicted value of $E_{\text{isc}}$, especially as $k_{\text{r}}$ becomes close to 1. Considering that all predicted values of $E_{\text{isc}}$ in Table 6 where quenching through intersystem crossing was the actual mechanism (i.e., ${ \Pr }:{\text{Y}}_{3} {\text{Al}}_{5} {\text{O}}_{12}$, ${ \Pr }:{\text{Lu}}_{3} {\text{Al}}_{5} {\text{O}}_{12}$, ${ \Pr }:{\text{Y}}_{3} {\text{Al}}_{4} {\text{Ga}}_{1} {\text{O}}_{12}$, ${ \Pr }:{\text{Y}}_{3} {\text{Al}}_{3} {\text{Ga}}_{2} {\text{O}}_{12}$) agree well with the linear fit in Fig. 6, it is most likely that the error comes from an overestimate of $E_{\text{dc}}$. Additional Pr³⁺ based phosphors doped in hosts with large depressions should be tested to further test the accuracy and limitation of using the simple expression of Eq. (8).

Finally, using tabulated values of $U\left( {6,A} \right)$ in lieu of photoconductivity measurements can lead to potentially large differences in predicted values. For example, using the tabulated value of $U(6,{\text{REAlO}}_{3}$) [32] instead of photoconductivity measurements of GdAlO₃ [50] would have led to differences in predicted ${\text{Ce}}:{\text{REAlO}}_{3}$ quenching temperatures on the order of 300 K. Thus, when looking for high-temperature thermographic phosphors, it is important to confirm the results of the analysis when using the data tabulated by Dorenbos [24, 29, 32] by supplementing with as much additional data as possible to confirm the predictions.

5 Conclusions

A methodology was presented in this work using configurational coordinate diagrams in combination with energy diagrams to select potential thermographic phosphors for high-temperature gas thermometry applications. It is based on the work of Dorenbos [18, 23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] to locate the conduction band of the host material with respect to the electronic energy levels of the rare-earth ion dopants and the QMSCC model of Struck and Fonger [38,39,40,41] to describe the relative potential well shapes of the $4f^{N - 1} 5d$ and $4f^{N}$ electronic levels. This work investigated oxide hosts doped with trivalent ions. Overall, 58 ion-host combinations were investigated. It was found that Ce³⁺ based phosphors only underwent thermal quenching due to ionization to the conduction band, whereas thermal quenching for Pr³⁺ based phosphors can occur either through the conduction band or intersystem crossing, depending on the host structure. This is an advantageous result for Ce³⁺ phosphors because it is not as important to consider the relative lattice relaxation in each electronic configuration (i.e., $k_{\text{r}}$) when trying to predict thermal quenching.

Based on the analysis, Ce³⁺ doped ortho-phosphates (REPO₄) were chosen for further investigation. All three phosphors had high measured quenching temperatures ($T_{50} > 800 \,K$). Additionally, the quenching temperature for Ce:GdPO₄ of $T_{50} = 1000\, K$ was more than 150 K larger than previously seen for trivalent ions doped in oxide hosts to the best of our knowledge. Finally, temperature quenching data were gathered from this work and previous literature for 19 different phosphors. A linear relationship was found between the quenching temperature and each phosphors’ smallest characteristic energy gap ($E_{\text{dc}}$ or $E_{\text{isc}}$), providing additional confidence in the analysis. It should be noted that the uncertainties in this analysis can lead to errors in predicted quenching temperatures of up to 300 K. Thus, once a potentially promising phosphor is found, care must be taken to gather as much data on the electronic structure of the phosphor as possible. Still, the encouraging results provide hope that this analysis can be applied to find thermographic phosphor for gas thermometry at combustion temperatures.