1 Introduction

In recent years, non-diffracting optical beams have been gaining growing research interest. Longer depth of focus (DOF) and smaller focal spot are subjects of considerable interest from both theoretical and practical viewpoints. Such research interest arises from their practical applications in the fields of optical data storage [1,2,3], material processing [4], optical coherence tomography [5,6,7], lithography, and other uses. Several methods have been proposed to generate non-diffracting optical beams. However, it was not until recent decade that related methods became mature and available, which include, for example, an achromatic hybrid refractive-diffractive lens with an extended DOF that works in the entire visible light band was designed and fabricated [8]. In the work by Lin et al., a longitudinally polarized focused beam with a DOF as long as 9λ was numerically demonstrated using the amplitude filtering technique based on Euler transformation [9]. Xiang Hao et al. demonstrated that a sharper focal spot area can be generated (0.147λ 2) by using an azimuthally polarized beam propagating through a vortex 0–2π phase plate than for radial polarization (0.17λ 2) under the same condition [10]. Yuan et al. proposed an approach to the generation of non-diffracting quasi-circularly polarized beams by a highly focusing azimuthally polarized beam using an amplitude modulated spiral phase hologram, which can be non-diverging over a relatively long axial range of ∼7.23λ [11]. Suresh et al. present a theoretical approach to generate a non-diffracting beam propagating without divergence (DOF) for over 11.454λ with reduced focal spot size of 0.384λ [12]. And C. Mohana Sundaram et al. proposed multi belt spiral phase modulation scheme with high NA lens for the incident azimuthally polarized doughnut Gaussian beam to generate a needle of transversely polarized beam with super long focal depth (49λ) and sub wave length focusing (0.48λ) [13].

For many applications, obtaining a very narrow non-diffracting beam with a tunable axial extent is desirable. For instance, the focal point possessing a small transverse dimension but a long focal depth is useful in optical data storage [14]. In fact, the long DOF can be achieved using diffractive optical elements, and they are able to reduce the compromise between the NA and the DOF that determine the lateral and axial resolutions in a conventional optical imaging system, respectively [15]. In addition, it has been shown in both theoretically and experimentally that a parabolic mirror (PM) can focus a radially polarized laser beam to a considerably tighter focal spot than what can be achieved with an aplanatic lens (AL) [16,17,18]. The PM seems to be an especially useful alternative for high-NA focusing given its simplicity and high-intensity throughput [16]. The tight focusing of azimuthally polarized beams focused by a high-NA AL has been studied. However, to our knowledge, the DOF of the non-diffracting beam generated by focusing azimuthally polarized beams can only reach about 49λ. Honestly, 11λ is far from extending the DOF of the focal spot. 49λ is still not long enough. In the actual situation, we are interested in generating a very narrow non-diffracting beam with a longer DOF by focusing azimuthally polarized beams. In this sense, motivated by the tight focusing of a narrow annulus of radially polarized beam [19], we consider the more realistic case of an azimuthally polarized illumination having the shape of a Gaussian annulus.

2 Configuration and theory

In this paper, we theoretically demonstrate the method to generate a non-diffracting beam with a tunable DOF while achieving its size in horizontal plane on a small level by focusing azimuthally polarized beams.

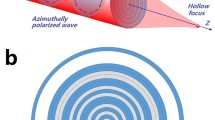
Schematic of the setup is shown in Fig. 1. A narrow annulus of azimuthally polarized beam illuminates on the phase mask and the generated beam is focused by the high-NA PM. The azimuthally polarized beam has the shape of a Gaussian annulus l 0(θ) = (π 1/2Δθ/2)−1exp[−(θ − θ 0)2/(Δθ/2)2], where ∆θ is the angular width of the incident annulus of azimuthally polarized beam. One should be pointed out is that the azimuthally polarized beam is a Gaussian distribution only for the incident angle θ and it makes the following calculations more concise and convenient. Such beam with azimuthally polarization would possess inspiring specialties if propagating through an ideal focusing system without aberrations. With the help of the vector diffraction theory [20, 21], we now analyze an azimuthally polarized annular beam focused by a PM. Under the phase mask, the electric field near the focus can be derived in the following form

$$ \vec{E}(r,\phi ,z) = \left[ {\begin{array}{*{20}c} {E_{r} } \\ {E_{\phi } } \\ {E_{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - Ae^{i\phi } (I_{0} + I_{2} )} \\ { - iAe^{i\phi } (I_{0} - I_{2} )} \\ 0 \\ \end{array} } \right], $$
(1)

where

$$ I_{n} = \int\limits_{{\theta_{{\rm min} } }}^{{\theta_{{\rm max} } }} {q(\theta )\sin \theta l_{0} (\theta )e^{ikz\cos \theta } J_{n} (kr\sin \theta ){\text{d}}\theta } . $$
(2)

Here, θ max represents maximum focal angle (θ max = arcsin(NA)) and θ min represents minimum focal angle. NA is the numerical aperture of the PM (NA = 1). K is the wavenumber in free space. J n (θ) denotes the nth-order Bessel function of the first kind. The apodization factor of the PM is q(θ) = 2/(1 + cosθ) [16].

Fig. 1
figure 1

The configuration of the proposed system for the formation of non-diffracting beams with a tunable longitudinal extent

Full size image

The goal of this paper is to propose a method for generating a narrow non-diffracting beam with a tunable axial extent by focusing azimuthally polarized beams. Based on numerical calculation, it is possible to analyze the effects of the focusing angle θ 0 and the angular thickness ∆θ of the annular illumination on the DOF. We perform the integration of Eq. (1) numerically by changing the parameter ∆θ. A focusing angle of 90° can be achieved with a PM focusing system and θ max = 90°. Considering θ 0 = (π − ∆θ)/2, it is obvious that only the parameter ∆θ has a significant impact on the relative amplitude of the electric field at focus. We consider the condition that ∆θ is much smaller than θ 0 for the range of angular thickness 0 ≤ ∆θ ≤ 0.2 rad. And we evaluate the length of the focal line in the longitudinal direction. Detailed analysis and comparison are made with past achievements by other works.

Figure 2 shows the normalized comparison plot of the total electric field along the axial direction (r = 0). It is shown that when ∆θ = 0.2 rad, the DOF of the non-diffracting beam is about 4.6λ. In the following steps, we continue to reduce the ∆θ. One can see that when ∆θ = 0.08 rad, the DOF is about 11.4λ which is very close to 11.454λ obtained by tight focusing of an azimuthally polarized beam with a circular symmetrical binary phase mask [12]. It should be pointed out that when ∆θ = 0.01 rad, the DOF is about 91.4λ which is 20 times that of ∆θ = 0.2 rad. If we pay close attention to the intensity distribution along the z axis, it is inspiring that a curve with a uniform axial flattop can be observed. This hints that in principle, the central part of the focal spot is “purely” uniform and possesses the highest intensity. Obviously, the smaller ∆θ, the longer DOF of the non-diffracting beam and a long DOF (91.4λ) can be achieved.

Fig. 2
figure 2

The normalized comparison plot of the total electric field along the axial direction

Full size image

3 Discussion

Based on an azimuthally polarized illumination having the shape of a Gaussian annulus (0 ≤ ∆θ ≤ 0.2 rad and ∆θ ≪ θ 0), it is possible to evaluate analytically the integrals in Eqs. (1). In this case, J 0(krsinθ) ≈ J 0(kr), J 2(krsinθ) ≈ J 2(kr) and the practical expressions for the components of the electric field in the focal region can be expressed as following

$$ \begin{aligned} E_{r} (r,\phi ,z) \approx - Ae^{i\phi } [J_{0} (kr) + J_{2} (kr)]\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - \Delta \theta }}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {q(\theta )l_{0} (\theta )\sin \theta e^{ikz\cos \theta } {\text{d}}\theta } \\ = - Ae^{i\phi } [J_{0} (kr) + J_{2} (kr)]q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - \Delta \theta }}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {\sin \theta e^{ikz\cos \theta } {\text{d}}\theta } \\ \approx \frac{{ - Ae^{i\phi } [J_{0} (kr) + J_{2} (kr)]q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )}}{ikz}(e^{ikz\Delta \theta } - 1) \\ E_{\phi } (r,\phi ,z) \approx - Ae^{i\phi } [J_{0} (kr) - J_{2} (kr)]\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - \Delta \theta }}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {q(\theta )l_{0} (\theta )\sin \theta e^{ikz\cos \theta } {\text{d}}\theta } \\ = - Ae^{i\phi } [J_{0} (kr) - J_{2} (kr)]q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - \Delta \theta }}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {\sin \theta e^{ikz\cos \theta } {\text{d}}\theta } \\ \approx \frac{{ - Ae^{i\phi } [J_{0} (kr) - J_{2} (kr)]q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )}}{ikz}(e^{ikz\Delta \theta } - 1), \\ \end{aligned} $$
(3)

where θ ε is a constant and π/2 − Δθ ≤ θ ε ≤ π/2 (integral mean value theorem).

The electric energy density in the focal region is proportional to the square modulus of the electric field of the beam

$$ \begin{aligned} \left| {E_{r} (r,z)} \right|^{2} \approx \frac{{[A(J_{0} (kr) + J_{2} (kr))q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )]^{2} }}{{(kz)^{2} }}2[1 - \cos (kz\Delta \theta )] \hfill \\ \left| {E_{\phi } (r,z)} \right|^{2} \approx \frac{{[A(J_{0} (kr) - J_{2} (kr))q(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )]^{2} }}{{(kz)^{2} }}2[1 - \cos (kz\Delta \theta )]. \hfill \\ \end{aligned} $$
(4)

The total electric energy density

$$ \begin{aligned} \left| {E(r,z)} \right|^{2} = \left| {E_{r} (r,z)} \right|^{2} + \left| {E_{\phi } (r,z)} \right|^{2} \\ \approx \frac{{[Aq(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )]^{2} 2[J_{0}^{2} (kr) + J_{2}^{2} (kr)]}}{{(kz)^{2} }}2[1 - \cos (kz\Delta \theta )]. \\ \end{aligned} $$
(5)

Especially on the focal plane (z = 0), the total electric energy density

$$ \left| {E(r,0)} \right|^{2} \approx [Aq(\theta_{\varepsilon } )l_{0} (\theta_{\varepsilon } )]^{2} 2[J_{0}^{2} (kr) + J_{2}^{2} (kr)](\Delta \theta )^{2} . $$
(6)

The length of the focal line is defined by the FWHM of its intensity profile in the longitudinal direction. From Eqs. (5), (6), we determined the longitudinal length (FWHM) of the non-diffracting beam

$$ \left| {E(r,z)} \right|^{2} = \frac{1}{2}\left| {E(r,0)} \right|^{2} . $$
(7)

By simplifying Eq. (7), an explicit but approximate result can be obtained

$$ \sin^{2} \left( {\frac{kz\Delta \theta }{2}} \right) = \frac{1}{2}\left( {\frac{kz\Delta \theta }{2}} \right)^{2} $$
(8)

It has to be noted that this approximation requires a relatively small value of ∆θ. Whereas for a very thin annulus (0 ≤ ∆θ ≤ 0.2 rad), the solution of Eq. (8) reveals the approximate relationship between ∆θ and DOF. By numerically solving the Eq. (8), kz∆θ ≈ 2.784 and we obtained the DOF = 2z ≈ 2.784λ/(π∆θ). We can see that the DOF of the non-diffracting beam in the z-direction is proportional to the wavelength λ and is inversely proportional to the angular width ∆θ of the annulus of incident azimuthally polarized beams. Therefore, the extent of the DOF can be tuned by changing the value of ∆θ. With this method, a non-diffracting focus line with a tunable longitudinal extent can be generated.

One should be pointed out is that the extending DOF generally follows with unwilling increase of the spot size in the transverse direction. Hence, there is a trade-off between them. Now we turn our attention to the width of the non-diffracting beam in the transverse direction. The width of the focal line is defined by the FWHM of its intensity profile in the transverse direction. It should be noted that the values of the transverse FWHM are approximately dependent on the choice of θ max, especially when the annulus of azimuthally polarized beam is very narrow. Harold Dehez etc. have proved that with a parabolic mirror and a focusing angle of 90°, the transverse FWHM is increased by less than 1% from the theoretical focusing limit of 0.36λ when ∆θ ≤ 0.2 rad and such a range of thickness is easily feasible experimentally [19]. In this paper, calculations show that the transverse FWHM is about 0.37λ and the variation in lateral confinement can be kept to negligible values for the range of angular thickness 0.01 ≤ ∆θ ≤ 0.2 rad. Hence, with this method, it is possible to tune the extent of the focal spot while keeping the transverse FWHM near the ideal value of 0.36λ.

The intensity profiles of the radial component, the azimuthal component, and the total field in the focal region are presented in Fig. 3a–c, respectively when ∆θ = 0.01 rad.

Fig. 3
figure 3

The normalized intensity profiles of the radial component (a), the azimuthal component (b), and the total field (c) in the focal region

Full size image

It is seen that the focal line are prominently elongated and the DOF is about 91.4λ. The intensity distribution of the non-diffracting beam exhibits an oscillatory behavior with side lobes in the transverse direction while it follows a Gaussian function in the longitudinal direction. It has been mentioned that the approximate relationship between ∆θ and DOF is valid for 0.01 ≤ ∆θ ≤ 0.2 rad with the PM (θ max = 90°). The approximate relationship shows that it is always possible to stretch the non-diffracting beam using smaller values of ∆θ. Actually, if the value of the angular thickness ∆θ is continuously decreasing, it is possible to further extend the DOF of the non-diffracting beam. However, anyone attempting to do so will face the risk of lack of adequate power for focusing because the annulus of azimuthally polarized beam is too narrow. In this paper, the method proposed here is based on the amplitude modulation, phase mask, azimuthally polarized beams and finally being focused by the high NA PM. Therefore, it is possible to achieve a long DOF (91.4λ) with reduced focal spot (0.37λ), high homogeneity and a relatively small beam area by focusing azimuthally polarized beams. And it is also not necessary to make the compromise between the DOF and focal size.

4 Conclusion

In summary, we theoretically proposed the generation of non-diffracting sub-half-wavelength focal spot with a tunable depth of focus by focusing a narrow annulus of azimuthally polarized beam with a high-NA PM system. Based on analytical expressions of the electric field in the focal region, we present the expression of the approximate relationship between the angular thickness ∆θ and DOF. The longitudinal extent of the focal line is then tunable by simply changing the thickness of the annular azimuthally polarized beams. The unique specialties such non-diffracting beam possesses implies that this method could be adopted in a wide range of practical domain, such as optical manipulation, optical micromachining, photolithography, especially two-photon polymerization technology to realize resolution beyond the diffraction limit [22].