1 Introduction

The precise measurement of angular velocity using gyroscopes is vitally important for inertial navigation systems (INSs). Optical gyroscopes exploit the Sagnac effect, which was discovered by Sagnac in 1936. The first demonstration of an optical gyroscope was in 1962, two years after the invention of the laser. Compared with other gyros, optical gyros are rapidly developed owing to their unique advantages of complete solid-state, high reliability, resistance to shock impact, long service life, wide dynamic range, rapid start-up, and low-angle random walk [1].

Scientists have reported that slow light has considerable potential for application in quantum information processing, information storage, and nonlinear optics [2,3,4,5,6,7,8,9,10,11]. In recent years, slow-light techniques have been used to enhance the sensitivity of measurements of angular velocity [11,12,13,16,12,13,14,15,].

In this paper, a high-sensitivity slow-light angular velocity sensor comprising a tunable asymmetrical double-ring structure (TADRS) coupled by a 3 × 3 coupler is presented. The phase difference caused by the TADRS between the counter-propagating waves is derived and simulated. The theoretical results show that the maximum phase shift difference of TADRS is two times larger than that of a single-ring system. The simulation results show that the maximum phase shift difference of TADRS occurs when the light power is amplified 1.85 times in one cavity while attenuated 79% in another. We designed and built an experimental system to verify the theoretical results. A section of erbium-doped fiber is added in the cavity with long fiber length and an attenuator is added in another ring. The one-way gain coefficient in each ring can be tuned to the value we want by adjusting the pump power and the attenuator. In order to suppress the spontaneous emission noise in erbium-doped fiber, we add two fiber Bragg gratings, which are connected to the optical path by two three-port optical circulators. Each fiber Bragg grating eliminates the optical noise returning back to the Y waveguide. The interference spectra of the two counter-propagating waves are used to calculate the phase shift differences at different angular velocities. The linear working region of the TADRS system is about ±5º/s. A square wave, whose half cycle equals to the group delay time of the system, is introduced to produce a bias phase in the optical path. The optimum sensitivity, which can be enhanced by more than three orders of magnitude theoretically, is enhanced no more than two orders of magnitude experimentally.

2 Sagnac effect of the TADRS

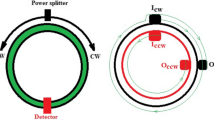
The TADRS is shown in Fig. 1. The structure consists of an input–output fiber and a tunable asymmetrical two-ring resonator, which is coupled by a 3 × 3 coupler. The transmission matrix of the 3 × 3 coupler can be written as [17]

$$\left[ {\begin{array}{*{20}c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} p & q & q \\ q & p & q \\ q & q & p \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {E_{10} } \\ {E_{20} } \\ {E_{30} } \\ \end{array} } \right] ,$$
(1)

where p = exp(j2kz), q = exp(−jkz), k is the coupling coefficient, and z is the coupling length of the coupler.

Fig. 1
figure 1

Schematic of tunable asymmetrical double-ring structure

Full size image

The relationship between the amplitudes of E 2 and E 20 (E 3 and E 30) can be expressed as

$$E_{20} = \alpha_{1} E_{2} e^{{i\phi {\kern 1pt}_{1} }} ,$$
(2)
$$E_{30} = \alpha_{2} E_{3} e^{{i\phi_{{{\kern 1pt} 2}} }} ,$$
(3)

where ϕ 1 = n e ωL 1/c; ϕ 2 = n e ωL 2/c; n e is the effective refractive index of the fiber core; ω is the angular frequency of the light; c is the speed of the light; L 1 and L 2 are the length of each ring; and α 1 = γ 1/2·α 1′(α 2 = γ 1/2·α 2′), where α 1′(α 2′) is the attenuation coefficient of the amplitude of the light after the light has traveled a distance L 1 (L 2), and γ is the attenuation coefficient of the light power after the light has traveled through the coupler.

The response of the TADRS between the input and output waveguides can be described as

$$T = \left| T \right|\exp (i\varPhi ) = \frac{{ - \alpha_{1} \alpha_{2} + \left( {t^{2} - r^{2} } \right)\left( {\alpha_{2} e^{{ - i\phi_{{{\kern 1pt} 1}} }} + \alpha_{1} e^{{ - i\phi_{{{\kern 1pt} 2}} }} } \right) - te^{{ - i\left( {\phi {\kern 1pt}_{1} + \phi_{{{\kern 1pt} 2}} } \right)}} }}{{\alpha_{1} \alpha_{2} (r^{2} - t^{2} ) + \alpha_{2} te^{{ - i\phi_{{{\kern 1pt} 1}} }} + \alpha_{1} te^{{ - i\phi_{{{\kern 1pt} 2}} }} - e^{{ - i\left( {\phi {\kern 1pt}_{1} + \phi_{{{\kern 1pt} 2}} } \right)}} }}{\kern 1pt} ,$$
(4)

where t = (p + 2q)/3; r = (p−q)/3; |t|2 denotes the fraction of the power output that is transmitted directly through each fiber; |r|2 denotes the fraction of power output coupled to the other fibers; Φ is the total phase introduced by the TADRS; and T is the transmission coefficient of the TADRS.

Figure 2 shows the relationship between the total phase shift difference and the attenuation coefficients in the two rings under the condition that the coupling ratio of the coupler is 1:1:1, the wavelength of the light is 1553 nm, and the lengths of the two rings are 2 m and 1 m. It can be seen from Fig. 2, most values of the phase shift difference of the system are small, when the attenuation coefficients of the two rings change from 0 to 2 in the process of system. The phase difference is maximum only when the coefficient of one ring is about 1.85, and another is about 0.2.

Fig. 2
figure 2

2D contour map of phase shift difference versus one-way total attenuation coefficients with k × z=2π/9, λ = 1553 nm, L 1 = 2 m, and L 2 = 1 m

Full size image

So if we add an optic amplifier in fiber ring 1 and an attenuator in fiber ring 2, adjust the amplifier and attenuator, the best sensitivity will be obtained.

When the system is under rotation conditions, the round-trip phase shifts between the counter-propagating waves can be expressed as

$$\phi_{i(\omega ,\varOmega )}^{ \pm } = n_{e} \omega L_{i} /c \pm N_{i} \frac{2\omega A}{{c^{2} }}\varOmega ,$$
(5)

where N i (i = 1, 2) is the number of loops in each ring, A is the area enclosed by the loops, and Ω is the angular velocity. The sign of the phase shift is positive (+) for the wave propagating clockwise and negative (−) for the wave propagating counterclockwise.

As the group delay can be written as τ g  = ∂Φ/∂ω, ∂Φ/∂ω = (∂Φ/∂ϕ 1)·(∂ϕ 1/∂ω) + (∂Φ/∂ϕ 2)·(∂ϕ 2/∂ω), and ϕ 2 = L 2 ϕ 1/L 1, so ∂Φ/∂ω = 2(∂Φ/∂ϕ 1)·(∂ϕ 1/∂ω). This means that the maximum group delay of the system will be achieved as long as one of the two rings is in the resonant state. It does not matter if the other ring is in the state of resonance. As is shown in Fig. 3, the maximum group delay of the double-ring system is twice larger than that of a single-ring system. The single-ring system can be achieved by breaking the fiber ring 2, and the loss (gain) of the fiber ring 1 is tuned until the group delay reaches the maximum.

Fig. 3
figure 3

Group delay time of the double-ring and single-ring resonant systems with the same full width at half maximum of spectrum

Full size image

When the structure is in the resonant state, the resonant frequency ω 0, at which the highest dispersion occurs, satisfies n e ω 0 L 1 /c = 2 mπ, where m is a positive integer. When ΩR ≪ c, we obtain.

$$\frac{{n_{g} }}{{n_{e} }} = 2\frac{\partial \varPhi }{{\partial \phi_{{{\kern 1pt} 1}} }} = 2\frac{{n_{{{\kern 1pt} 1g}} }}{{n_{e} }} ,$$
(6)
$${\text{d}}\varPhi = 2\frac{{{{\partial \varPhi } \mathord{\left/ {\vphantom {{\partial \varPhi } {\partial \omega }}} \right. \kern-0pt} {\partial \omega }}}}{{{{\partial \phi_{{{\kern 1pt} 1}} } \mathord{\left/ {\vphantom {{\partial \phi_{{{\kern 1pt} 1}} } {\partial \omega }}} \right. \kern-0pt} {\partial \omega }}}}{\text{d}}\phi_{{{\kern 1pt} 1}} .$$
(7)

The phase difference between the two counter propagating waves can thus be expressed as

$$\Delta \Phi (\omega ,\Omega ) = 4\int\limits_{{\phi \left( {\omega ,0} \right)}}^{{\phi \left( {\omega ,\Omega } \right)}} {\frac{{n_{{1g}} }}{{n_{e} }}} d\phi _{1}.$$
(8)

So in theory, the ultimate sensitivity of the double-ring system to detect angular velocity is twice as large as the single-ring system.

Figure 4 shows the phase differences introduced by the TADRS, for different rotation velocities, with α 1 = 1.85, α 2 = 0.21, and |t|2 = 0.33. Combining Eq. (8) and Fig. 4, we can see that the phase difference \(\Delta \varPhi_{(\omega ,\varOmega )} = \varPhi_{(\omega ,\varOmega )}^{ + } - \varPhi_{(\omega ,\varOmega )}^{ - }\) is maximized at ω 0, so in practice we measure \(\Delta \varPhi_{{\left( {\omega_{0} ,\varOmega } \right)}}\) for high sensitivity.

Fig. 4
figure 4

Phase differences introduced by the TADRS under different rotation velocities, with α 1 = 1.85, α 2 = 0.21

Full size image

In Fig. 4, we can see that the maximum phase difference of TADRS is about 2.7 rad, when Ω = 0.2π rad/s. However, for the same conditions of Ω and fiber length, the Sagnac phase difference is only about 0.0034 rad. Therefore, the sensitivity of the slow-light gyroscope in our case can be enhanced by more than 1000 times.

As we can see in Fig. 5, at the resonant frequency, ∆Φ changes linearly when ∆ϕ(Ω < 5°/s) is very small. Equation (8) can be approximately written as

$$\Delta \varPhi_{{\left( {\omega_{0} ,\varOmega } \right)}} \approx \frac{{n_{{1g\left( {\omega_{0} } \right)}} }}{{n_{e} }}\Delta \phi = \frac{{n_{{1g\left( {\omega_{0} } \right)}} }}{{n_{e} }}N\frac{{8\omega_{0} A}}{{c^{2} }}\varOmega ,$$
(9)
Fig. 5
figure 5

Phase shift difference and normalized intensity versus rotation rate

Full size image

According to the analysis above, in order to make the double-ring resonator system to achieve its best sensitivity, we use the structure shown in Fig. 1. A section of erbium-doped fiber is added in the ring with long fiber length; thus the one-way gain coefficient can be tuned to the value we want by adjusting the pump power. A power attenuator A 1, which is made by winding a section of fiber around a piezoelectric ceramic with small diameter, is added to the ring 2. The value of the optical power attenuation can be tuned by changing the number of turns of the optical fiber. Another effect of the piezoelectric ceramic is that the length of the fiber ring can be finely adjusted by changing the voltage applied to the piezoelectric ceramic so that this ring is also working in the resonant frequency.

3 Experiments

The experimental setup is shown schematically in Fig. 6. In our experiments, the key parameters of the double-ring slow-light structure were n e  = 1.5, L 1 = 2 m, L 2 = 1 m, |t|2 = 0.33, γ = 0.5 dB, α 1 = 1.85, and α 2 = 0.21. The center wavelength is 1553 nm. The function generator is used to linearly tune wavelength by sending a triangular voltage signal to the tunable laser; thus the interference spectra can be obtained. The light signal from the tunable laser enters a Y waveguide and is equally divided into two beams. The Y waveguide integrates a phase modulator and a polarizer. The two beams are launched into the TADRS and travel in opposite directions. In order to ensure the reciprocity of the system, bidirectional pumping mode is used in the erbium doped fiber amplifier.

Fig. 6
figure 6

Configuration of experimental setup of tunable asymmetrical double-ring structure rotation sensor

Full size image

In order to suppress the spontaneous emission noise in erbium doped fiber, we add two fiber Bragg gratings, which are connected to the optical path by two three-port optical circulators. Each fiber Bragg grating eliminates the optical noise returning back to the Y waveguide. The central wavelength of each fiber grating is equal to 1553 nm. The two counter-propagating waves meet at the Y waveguide again and interfere. The interference light travels through the 3-dB coupler again and reaches the detector, which converts it into an electrical signal that is analyzed by an oscilloscope.

The interference spectrum detected by the detector can be written as

$$I_{{D(\omega ,{\kern 1pt} \varOmega )}} = I_{{(\omega ,{\kern 1pt} \varOmega )}}^{ + } + I_{{(\omega ,{\kern 1pt} \varOmega )}}^{ - } + 2\sqrt {I_{{(\omega ,{\kern 1pt} \varOmega )}}^{ + } \cdot I_{{(\omega ,{\kern 1pt} \varOmega )}}^{ - } } \cos \left( {\Delta \varPhi_{{(\omega ,{\kern 1pt} \varOmega )}} } \right) ,$$
(10)

where I ±(ω,Ω ) are the two counter-propagating output light signals of the TADRS at the rotation speed Ω and the light frequency ω. Interference spectra measured with different values of α 1 and α 2 at different rotary velocities are shown in Fig. 7a, c. Compare Fig. 7a and c, and we can find that when α 1 ≈ 1.85 and α 2 ≈ 0.21, the changes of the normalized intensity are more obvious, and the sensitivity of the system reaches the highest.

Fig. 7
figure 7

Interference spectra of the TADRS with different vlues of α 1 and α 2 at different rotary velocities. a α 1 ≈ 1.85, α 2 ≈ 0.21, and phase bias is not included; b α 1 ≈ 1.85, α 2 ≈ 0.21 with phase bias ϕ b  = ±π/2; c α 1 ≈ 1.8, α 2 ≈ 0.21 without phase bias; d α 1 ≈ 1.8, α 2 ≈ 0.21 with phase bias ϕ b  = ±π/2

Full size image

Near the resonance frequency ω 0, \(I_{{(\omega_{0} ,\varOmega )}}^{ \pm }\) are symmetric about ω 0, and \(I_{{(\omega_{0} ,\varOmega )}}^{ \pm } = I_{{(\omega_{0} ,\varOmega )}}^{ - } = I_{{(\omega_{0} ,\varOmega )}}\). When at ω 0, the light intensity detected by the detector can be written as:

$$I_{{D(\omega_{0} ,\varOmega )}} = 2I_{{\left( {\omega_{0} ,{\kern 1pt} \varOmega } \right)}} \left( {1 + \cos \left( {\Delta \varPhi_{{\left( {\omega_{0} ,{\kern 1pt} \varOmega } \right)}} } \right)} \right)$$
(11)

In order to obtain \(\Delta \varPhi_{{(\omega_{0} )}}\), we require knowledge of \(I_{{{\text{D}}(\omega_{0} ,\varOmega )}}\) and \(I_{{(\omega_{0} ,\varOmega )}}\). When the input value is close to zero, the cosine function exhibits the lowest sensitivity. We must therefore consider how to achieve the highest sensitivity for small input rotation rates.

In order to let the system work in the linear region and obtain high sensitivity, a square wave is added to the Y waveguide phase modulator [18]. The square wave is expressed as \(\phi_{b} = \pm \pi /2\), having a frequency of \(1/2\tau_{g}\), where \(\tau_{g}\) is the group delay of the TADRS at the frequency ω 0.

The detector intensity difference between the π/2 state and the −π/2 state can be written as

$$\Delta I_{{D\left( {\omega_{0} ,\varOmega } \right)}} = I_{0} \cdot \sin \Delta \varPhi_{{\left( {\omega_{0} ,\varOmega } \right)}} ,$$
(12)

where \(I_{\text{D}} = 4I_{{(\omega_{0} ,\varOmega )}}\), which can be obtained by adding up the intensities in the two modulation states. Figure 7b and d shows the interference spectra measured with different values of α 1 and α 2 at different rotary velocities when the square wave is introduced. Compare Fig. 7b and d, and we can find that the result is the same after adding the bias modulation. The changes of the normalized light intensity after adding the bias modulation are greater than the changes of the normalized light intensity without modulation. The sensitivity of the system is further improved.

As discussed above, when the angular rate is small, ∆Φ is linear with Ω. Then we can demodulate the angular velocity signal, which can be written as

$$\varOmega = \frac{{n_{e} }}{{n_{{1g\left( {\omega_{0} } \right)}} }} \cdot \frac{{c^{2} }}{{8N\omega_{0} A}} \cdot \frac{{\Delta I_{\text{D}} }}{{I_{0} }} = k^{\prime}\frac{{\Delta I_{\text{D}} }}{{I_{0} }}$$
(13)

where scale factor k´ can be obtained by measuring ∆I D/I 0. Figure 8 gives the relation between the sensitivity enhancement factor ∆Φ/∆ϕ of the system and α 1, α 2. It can be seen from Fig. 8, when α 1 ≈ 1.85 and α 2 ≈ 0.21, the sensitivity enhancement factor reaches the maximum, the results are consistent with theoretical analysis.

Fig. 8
figure 8

Sensitivity enhancement scale factor versus different values of α 1 and α 2

Full size image

The minimum angular velocity that the TADRS can measure is limited by the shot noise of the detector. The light power standard deviation can be written as

$$\sigma_{P} /\sqrt {\Delta f_{bw} } = \sqrt {2 \cdot \left( {hc/\lambda } \right) \cdot P_{0} } .$$
(14)

According to formula (10), the standard deviation of the angular velocity can be written as

$$\sigma_{\varOmega } /\sqrt {\Delta f_{bw} } = \frac{{n_{e} c^{2} }}{{8N\omega_{0} An_{{1g\left( {\omega_{0} } \right)}} }} \cdot \frac{{\sqrt {2hc/\lambda_{0} } }}{{\left| {\sin \phi_{b} } \right| \cdot \sqrt {P_{0} } }} .$$
(15)

In our case, n 1g/n e ≈ 1000, P 0 = 1mw, ∆f bw  = 1 Hz, |sinϕ b| = 1, the standard deviation of the angular velocity is less than 0.001º/√h.

The measuring limitation of the resonant angular velocity sensor is determined by the following formula:

$$\sigma_{\varOmega } /\sqrt {\Delta f_{bw} } = \frac{{\lambda_{0} c}}{4NAF} \cdot \frac{{\sqrt {2hc/\lambda_{0} } }}{{\sqrt {P_{0} } }} ,$$
(16)

where F is the fineness of the resonator and \(F \approx \frac{c}{{nL(\Delta \omega )_{{{\text{FWHM}}}} }}\), (∆ω)FWHM is full width at half maximum of spectrum. According to the current level of technology, the fineness of cavity is difficult to reach 1000. If F = 1000 (the actual fineness is less than 100), the standard deviation of the angular velocity of resonant angular velocity sensor is 0.0011º/√h. Compared with RAVS, TADRS has the same theoretical sensitivity.

4 Conclusion

In this study, we designed a tunable asymmetrical double-ring slow-light angular velocity sensor based on a 3 × 3 directional coupler, whose coupling ratio is 1:1:1. The principle whereby slow light improves the detection sensitivity was analyzed theoretically. The maximum phase shift difference of TADRS is two times larger than that of a single-ring system. To the best of our knowledge, this is the first time it is reported that the theoretical sensitivity of an optical angular velocity sensor is higher than that of a resonant optic gyroscope. If the center wavelength is 1553 nm, only when α 1 = 1.85 and α 2 = 0.21, ∆Φ reaches max. We use erbium-doped fiber to amplify the power and wind a section of fiber around a piezoelectric ceramic with small diameter to attenuate the power. The working area of the TADRS sensor is about ±5º/s. A square wave, whose half cycle equals to the group delay time of the system, is introduced to produce a bias phase in the optical path. The optimum sensitivity can be enhanced by more than three orders of magnitude theoretically. The saturation absorption effect of erbium-doped fiber and the accuracy of the attenuation of the attenuator will greatly reduce the sensitivity of the system. The minimum angular velocity that the TADRS can measure is in the same order of the magnitude with the resonant angular velocity sensor.