Optical reconstruction of non-diffracting beams via photorefractive holography

Abstract

This work presents the optical reconstruction of non-diffracting beams via photorefractive holography. Optical generation of non-diffracting beams using conventional optical components is difficult and, in some circumstances, unfeasible, as it is the case of wave fields given by superposition of non-diffracting beams, which have been successfully generated through computer-generated holograms reproduced in spatial light modulators. With the photorefractive holography technique, the hologram of a non-diffracting beam is optically constructed (recorded) and reconstructed (read) in a nonlinear photorefractive medium. The experimental realizations of non-diffracting beams (Bessel, Mathieus and Parabolic), the Bessel beam arrays and superposition of co-propagating Bessel beams (Frozen waves) are made in a photorefractive holography setup using a photorefractive Bi₁₂SiO₂₀ (BSO) crystal as the holographic recording medium. The results are in agreement with the theoretical predictions and are presenting excellent prospects for the implementation of this technique in dynamical systems with applications in optics and photonics.

1 Introduction

Non-diffracting waves are beams and pulses that keep their intensity spatial shape during propagation [1]. Pure non-diffracting beams include Bessel beams, Mathieus beams and parabolic beams [2–5]; also the superposition of these waves can produce very special diffraction-resistant beams, such as the Frozen waves [5, 6]. These beams could be applied in many fields, such as optical metrology, optical alignment systems over long distances and mechanical arrangements, optical tweezers, optics atom guidance, nonlinear optics, optical coherence tomography, imaging systems, optical communications in free space, among others [7–11].

The experimental generation of non-diffracting beams using conventional diffractive optical components presents several difficulties, such as co-propagating beam superposition for instance, and in some cases is not feasible.

Holography has been presented as a powerful tool for generating special optical beams and in a wide range of other applications in the field of optics and photonics [12–23]. In fact, the computational holography technique [12–14] with the use of numerical holograms and spatial light modulators has efficiently reproduced the beams cited above [14–17]. In this case, the construction of the non-diffracting beam hologram is done numerically by a computer-generated hologram (CGH) and its reconstruction is performed optically with its implementation in a spatial light modulator (SLM).

On the other hand, photorefractive holography has been presented as a promising technique for dynamic holographic processes and holographic interferometry methods for analyzing surfaces and optical wavefronts [18–24]. This technique is based on the photorefractive effect, which consists of modulating the refractive index via photo induction of charge carriers and the linear electro-optic effect in some semiconductors crystals with special features, the so-called photorefractive crystals (LiNbO₃, SBN, KBT, BaTiO3, Bi₁₂SiO₂₀, among others) [18]. Since it is a process that occurs at electronic levels in semiconductor crystals with nonlinear optical properties, the holographic gratings feature high resolution and short response time, making it possible to act as holographic recording media. These do not require chemical or computational processing for reconstruction of the holographic image and present indefinite reusability [18–24].

In this work, used the photorefractive holography technique, where the non-diffracting beam holograms are optically constructed (recorded) and reconstructed (read) in a photorefractive nonlinear medium by means of the refractive index modulation generated via a second-order nonlinear effect (Pockels effect). The experimental realization of the beams is performed in a photorefractive holography setup, using a photorefractive sillenite crystal type Bi₁₂SiO₂₀ (BSO), as the holographic recording medium. Thus, Bessel, Mathieus and parabolic beams as well as the non-diffracting beams arrays and the superposition of co-propagating Bessel beams (Frozen waves) are successfully generated. The experiment begins in excellent agreement with the theoretical predictions and the results obtained via the computational holography technique. The results possess excellent potential for implementation in dynamical systems with scientific and technological applications.

2 Theoretical background

2.1 Non-diffracting beams

The Helmholtz equation $\left[ {\nabla^{2} + k_{0}^{2} } \right]\varPsi = 0 ,$ describes the propagation of light considering the effects of diffraction and scattering. Ideal non-diffracting waves are beams and pulses that keep unchanged their intensity pattern during propagation [1]. The ideal non-diffracting beams are characterized by a mathematical structure of the type $\varPsi = A\left( {x,y} \right) \times { \exp }\left( {ik_{z} z} \right) \times { \exp }( - i\omega t)$, where A(x, y) is the transversal function for a wave propagating along z-axis. In circular–cylindrical coordinate this function takes the form of a Bessel beam:

$$\varPsi (\rho ,\phi ,z,t) = J_{\nu } (k_{\rho } \rho )e^{{ik_{z} z}} e^{i\nu \phi } e^{( - i\omega t)}$$

(1)

where $J_{\nu } (.)$ is the Bessel function of the first kind of order $\nu$ and $k_{\rho }$ is the transverse wave number, which defines the transverse width of the beam. Taking the intensity, I(ρ), we see that the cross section is the square of a Bessel function of order $\nu$ independent of Z,

$$I(\rho ) = \left| {J_{\nu } \left( {k_{T} \rho } \right)} \right|^{2}$$

(2)

Other types of non-diffracting beam solutions can be obtained to the Helmholtz equation:

• in the elliptical–cylindrical coordinate system, there are the so-called Mathieus beams, for instance,

  $$\varPsi_{\text{e}} \left( {\eta ,\xi ,z,t;q} \right) = {\text{ce}}_{\text{m}} (\eta ,q){\text{Je}}_{\text{m}} \left( {\xi ,q} \right)e^{{ik_{z} z}} e^{ - i\omega t}$$

  (3)

  where ce and Je are the even angular and radial solution of the Helmholtz equation in elliptic coordinate, q = (f k ²_T )/4 and f is the semi focal ellipse distance; these beams are well described in Ref. [3] and

• in a parabolic–cylindrical coordinate system a non-diffracting beam with parabolic transversal shape was obtained, parabolic beams, for instance.

  $$\varPsi_{\text{e}} \left( {\mu ,\nu^{\prime},z,t;a} \right) = \frac{1}{\pi \sqrt 2 }\left| {\varGamma_{1} } \right|^{2} P_{\text{e}} (\sigma \nu^{\prime};a)P_{\text{e}} \left( {\sigma \mu^{\prime}; - a} \right)e^{{ik_{z} z}} e^{ - i\omega t}$$

  (4)

  where P _e is the even solution of Helmholtz equation in parabolic coordinates, $\left| {\varGamma_{1} } \right|$ is a constant given by gamma function, $\sigma = (2k_{\text{T}}^{2} )^{1/2}$ and a is a constant sometimes called beam order, and it defines the symmetry of the beam around the origin of the coordinate system. These beams are well described in Ref. [4].

In addition, with possible potential applications in optical tweezers, atom guidance and photonics in general, there are the non-diffracting beam arrays and the so-called frozen wave beams [5–7, 15–17]. The latter are made by a suitable superposition of co-propagating Bessel beams. Basically, the idea is to obtain diffraction-resistant beams whose desired longitudinal intensity pattern, |F(z)|², in the range 0 $\le$ z $\le$ L, can be chosen a priori. To obtain the desired beam, we consider the following solution given by a superposition of 2N + 1 co-propagating and equal frequency Bessel beams of order $\nu$:

$$\varPsi (\rho ,\phi ,z,t) = e^{ - i\omega t} \sum\limits_{n = - N}^{N} {A_{n} J_{\nu } (k_{\rho n} \rho )e^{{ik_{zn} z}} e^{i\nu \phi } }$$

(5)

where $k_{\rho n}^{2} = \omega^{2} /c^{2} - k_{zn}^{2}$ and with the choice $k_{zn}^{{}} = Q + 2\pi n/L$, where the parameter Q is a constant obeying $0 \le Q \pm (2\pi /L)N \le \omega /c$ and is related with the transverse dimensions of the resulting beam.

In solution of Eq. (5), the coefficients A _n are given by

$$A_{n} = \frac{1}{L}\int_{0}^{L} {F(z)e^{{ - i\frac{2\pi }{L}nz}} {\text{d}}z}$$

(6)

where |F (z)|² is the desired longitudinal intensity pattern in the 0 ≤ z ≤ L range. This longitudinal intensity pattern can be concentrated (as we wish); over the propagation axis (ρ = 0) by taking $\nu = 0$ in Eq. (5), i.e., we deal with zero-order Bessel beam superposition, or over a cylindrical surface. In this case, we deal with $\left| \nu \right| > 0$ values [7, 15–17].

2.2 Photorefractive holography

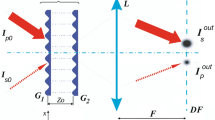
In photorefractive holography using photorefractive crystal (PRC) Bi₁₂SiO₂₀ as the recording medium [18–24], the holographic recording occurs by a refractive index modulation, via photorefractive effect in diffusive regimen. The refractive index modulation of the hologram is written as $\Delta n = n_{0}^{ 3} r_{ 4 1} E_{\text{sc}} / 2$, where n ₀ is the refractive index, r ₄₁ is the linear electro-optic coefficient of the sillenite crystal and E _sc is the electric field generated by the redistributed space charges in the crystal. The holographic reconstruction of the object wavefront occurs in quasi real time, where the optical reconstruction of the holographic image is a diffracted wave. If λ is the recording wavelength, $\alpha$ is the crystal rotator power, l is the crystal thickness, m is the modulation of the incident interference pattern and 2θ is the angle between the interfering beams, the diffraction efficiency of a hologram grating recorded in a PR crystal is given by [18–24],

$$\eta = \left( {\frac{\pi \Delta n}{\lambda \cos \theta }\frac{\sin \alpha l}{\alpha l}} \right)^{2} m^{2}$$

(7)

The intensity I ₀ at a point (x, y) resulting from the superposition of the diffracted (I _{0, D}) and the transmitted (I _{0, T}) intensities is given by

$$I_{0} (x,y) = I_{{0,{\text{T}}}} (x,y) + I_{{0,{\text{D}}}} (x,y)\left[ {1 - e^{( - t/\tau )} } \right]^{2}$$

(8)

where τ is the hologram response time (writing and erasure). The holographic reconstruction of the object wave, I _{0, D}(x, y), is written as

$$I_{{0,{\text{D}}}} (x,y) = I_{{0,{\text{O}}}} (x,y)\eta + I_{{0,{\text{R}}}} (x,y)\left[ {1 - \eta } \right] + 2gY\cos \Delta \varPhi$$

(9)

where I _{0, O}(x, y) and I _{0, R}(x, y) are the object and reference beam intensities, respectively, g is a parameter of the polarization coupling of the beams, $Y = [\eta (1 - \eta )I_{{0,{\text{O}}}} (x,y)I_{{ 0 , {\text{R}}}} (x,y)]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$is the interference term and $\Delta \varPhi$ is the phase shift on the object wave [18–24].

3 Experiments and results

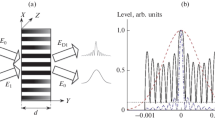
In this investigation, experimental setups for photorefractive holography were implemented as shown in Fig. 1, (a) without SLM and (b) with SLM for experimental generation of the non-diffracting beams.

Fig. 1

Photorefractive holographic setups for optical generation of non-diffracting beam: a without SLM, where Ms are mirrors, BSs are beam-splitters, FS is the spatial filter, Ls are lenses, Pols are polarizers, Mask is the concentric rings plate, BSO is the photorefractive crystal, Filter is the neutral density filter and CCD is camera for image acquisition; b with SLM, where SLM is a spatial light modulator, ID is the circular mask. H _CGH(x, y) is the computer-generated hologram of the non-diffracting beam and H _PRH(x, y) is the PR hologram of the non-diffracting beam. Ψ_teo(r, z = 0) is the theoretical function beam, Ψ_exp1(r, z = 0) is the SLM reconstruction of the experimental non-diffractive beam (transverse); Ψ_exp2(r, z = 0) is the PRH reconstruction of the experimental non-diffractive beam (transverse) and Ψ_exp2(r, z) is the orthogonal projection of PRH reconstruction of the experimental non-diffractive beam

In the setup without SLM (Fig. 1a), an Argon laser was used (λ = 514.5 nm and 1 W output power, at that wavelength the BSO crystal is more sensitive [18]), Ms are mirrors, BSs are beam-splitters, FS is a spatial filter, Ls are lenses, Pols are polarizers, Mask is a black plate with a ring transmittance, BSO is a sillenite Bi₁₂SiO₂₀ crystal is the holographic recording medium (with 10 × 10 × 3 mm³ dimensions and transverse electro-optical configuration), Filter is a neutral density filter and CCD camera for image acquisition (Imaging Source CCD Camera, 960 × 720 pixels and pixel size 4.65 μm). In this case, the Bessel beam (object beam) can be generated by Mask with a ring transmittance [2], Ψ_exp1(r, z = 0) is the experimental non-diffracting beam, and the PR hologram H _PRH(x, y) is optically recorded in the photorefractive crystal by interfering the object beam with the reference beam.

The reference and object beams are incident on the crystal surface at an angle of 45° between them, to optimize the diffraction efficiency [15–20]. Then, the optical reconstruction of this PR hologram (PRH) allows to obtain the non-diffracting beam, in this case by photorefractive holography, where Ψ_exp2(r, z = 0) is the PRH reconstruction of the experimental non-diffracting beam (transversal intensity pattern) and Ψ_exp2(r, z) is the orthogonal projection of PRH reconstruction of the experimental non-diffracting beam. Finally, the transversal intensity pattern of the reconstructed non-diffracting beam is recorded by a CCD camera “step by step” along the propagation axis defined by the distance of propagation invariant finite of the non-diffracting beam. The details of this method can be seen in references [19–24].

Consequently, a photorefractive holographic system that allows the experimental reconstruction of non-diffractive beams, particularly Bessel beams, was validated. Therefore, the photorefractive holographic system, with change in the parameters of Masks with concentric rings, a black plate with a ring transmittance, allows to record and to reconstruct Bessel beam arrays and make a co-propagating superposition of Bessel beams. This will be detailed in Sects. 3.1 and 3.2, respectively, using spatial light modulators.

As described previously, the photorefractive medium has a characteristic formation time of the spatial-charge field generated by an interference pattern (holographic recording). Thus, the intensity diffracted by the hologram increases exponentially with time until the holographic grating reaches its maximum diffraction efficiency under these conditions. The characteristic time is also related to the holographic grating erasure, in which the uniform intensity of the read beam erases the holographic grating, exponentially decreasing the intensity of the diffracted beam, in agreement with Eqs. (8) and (9). This has been taken into account when recording several beams, for example, beam arrays or co-propagating beams, as will be shown in the following sections.

On the other hand, the SLMs are known devices for experimental generation of non-diffractive beams via computational holography (computer-generated holograms, CGHs) [12–17], which allow greater flexibility in the generation of non-diffractive beams for validation of our system. Thus, the apparatus shown in Fig. 1b was proposed, where the SLM is used for generating special non-diffracting beams (Bessel, Mathieus, parabolic and Frozen waves); where, additionally, SLM is a spatial light modulator LC R1080 model (Holoeye Photonics, with a liquid crystal display of 1980 × 1200 pixels and pixel size 8.1 μm) and ID is the circular mask for frequency selection in the Fourier plane on a 4F-filter system [14–17]. In this case, the H_CGH(x, y) is the computer-generated hologram of the non-diffracting beam, Ψ_teo(r, z = 0) is generated by a computational calculation, and the Ψ_exp1(r, z = 0) is the experimental non-diffracting beam (transversal intensity pattern) obtained via SLM. Then, similar to the setup of Fig. 1a, the PR hologram H_PRH(x, y) is optically recorded in the photorefractive crystal by interference of the object beam with the reference beam. The optical reconstruction of this PRH allows to obtain the non-diffracting beam by photorefractive holography, where Ψ_exp2(r, z = 0) is the PRH reconstruction of the experimental non-diffracting beam (transversal intensity pattern) and Ψ_exp2(r, z) is the orthogonal projection of PRH reconstruction of the experimental non-diffracting beam.

3.1 Optical reconstruction of a single non-diffracting beam via photorefractive holography

Initially, the setup of Fig. 1, (a) without SLM and using the Mask with concentric ring [2] or (b) with SLM, was configured to optically generate a Bessel beam (object beam), and the setup of Fig. 1b with SLM, to optically generate any non-diffracting beam (object beam) [14–17]. Thus, the object and reference beams focus on the crystal (recording process of the photorefractive hologram), with a saturation time of the holographic grating of approximately 2.8 min, in agreement with photorefractive recording in this PR medium and conditions [18–22]. Then, the object beam is blocked and only the reference beam focuses on the crystal (reading process of the photorefractive hologram), which is diffracted by the holographic grating reconstructing the non-diffracting beam. The transverse patterns of the beam were captured by moving the CCD along the axis of propagation. The results agree with the theoretically predicted, as can be seen in each of the following cases.

3.1.1 First case

Using the setup of Fig. 1b, a zero-order Bessel beam with intensity $J_{0}^{ 2} (k_{\rho } \rho )$ was generated, where $k_{\rho } = 3. 8 \times 10^{ 4 } {\text{m}}^{ - 1}$ and the hologram aperture radius R = 1.1 mm [15–17], this has a maximum propagation of 40 cm. Figure 2 shows the intensity pattern in $\rho = 0$ (on-axis) over the propagation distance, predicted by the theoretical field encoded in numerical hologram (CGH), optical reconstruction by SLM and reconstruction of the hologram recorded in photorefractive medium. As seen in Fig. 2, the results agree with the theoretically expected, which was made by applying an apodization given by a Gaussian filter in the hologram (CGH) of the Bessel beam. Good results in the transverse intensity patterns of Bessel beams optically reconstructed via photorefractive holography are presented in Fig. 3. The images were captured at 2-s intervals from the beginning of the reading process, and spatially displaced by 2.5 cm.

Fig. 2

Comparison between the longitudinal intensity pattern in ρ = 0 for a Bessel beam predicted theoretically, generated by the SLM and reconstructed via photorefractive holography

Fig. 3

Longitudinal intensity pattern in ρ = 0 for a Bessel beam reconstructed via holography photorefractive with transverse pattern b 11 cm, c 21 cm, d 31 cm, and e 38.5 cm

3.1.2 Second case

Using the setup of Fig. 1b, the very interesting Mathieu beams were used for experimental validation of the technique. Using the numerical solution of Eq. (3), given by $\varPsi_{\text{e}} \left( {\eta ,\xi ,z} \right) = {\text{ce}}_{\text{m}} (\eta ,q){\text{Je}}_{\text{m}} \left( {\xi ,q} \right){\text{circ}}(\rho /R)$, for the fields to be implemented in numerical hologram and then reconstructed by the SLM, with parameters q = 22, k _T = 2.48 × 10⁴ m⁻¹, R = 1.2 mm and have maximum propagation of 60 cm [3]. The results of the reconstruction from photorefractive holograms are shown in Fig. 4, where the intensity patterns on the axis of propagation are in accordance with the expected theoretically.

Fig. 4

Longitudinal intensity pattern in ρ = 0 for a Mathieu beam reconstructed via holography photorefractive with transverse pattern b 10 cm, c 24 cm, d 39 cm, and e 51 cm

3.1.3 Third case

Similarly, to the previous case, Parabolic beams were reproduced using the numerical solution of Eq. (4), given by $\varPsi_{\text{e}} \left( {\mu ,\nu^{\prime},a} \right) = \frac{1}{\pi \sqrt 2 }\left| {\varGamma_{1} } \right|^{2} P_{\text{e}} (\sigma \nu^{\prime};a)P_{\text{e}} \left( {\sigma \mu^{\prime}; - a} \right){\text{circ}}(\rho /R)$, to the fields to be implemented in numerical hologram and then reconstructed by the SLM, with a = −5, k _T = 2.1 × 10⁴ m⁻¹, σ = (2k _T)^1/2, R = 0.6 mm and maximum propagation of 45 cm [4]. The results were in accordance with the expected theoretically and the photorefractive reconstruction of holograms is shown in Fig. 5.

Fig. 5

Longitudinal intensity pattern in a x = 0 and y = 0; 3 mm for a parabolic beam: reconstructed via holography photorefractive with transverse pattern b 11 cm, c 18 cm, d 29 cm, and e 40 cm

3.2 Optical reconstruction of non-diffracting beam arrays via photorefractive holography

The process for obtaining numerical fields and non-diffracting beam holograms allows to generate arrays or a certain transverse spatial distribution of N non-diffracting beams. Arrays of non-diffracting beams can be interesting for applications in optical tweezers, optical communications for a system with multiple channels and for generating solitons in a nonlinear crystal [24–26].

From the fields of these different non-diffracting beams $\psi \left( {x,y,z} \right)$, considering the origin of the displaced coordinate system on the plane transverse to the direction of propagation $\left( {x \pm \delta x;y \pm \delta y} \right)$, these displaced fields are summed up to form a total field $\varPsi_{\text{tot}} = \sum \psi \left( {x \pm \delta x;y \pm \delta y} \right)$, resulting in an interference pattern and from this generate a CGH for implementation and reconstruction using a SLM.

Consider a beam composition defined by four zero-order Bessel beams, such as

$$\begin{aligned} \psi_{1} \left( {x + \delta x,y + \delta y,z = 0} \right) = J_{0} \left( {k_{\rho } \sqrt {(x + \delta x)^{2} + (y + \delta y)^{2} } } \right) \hfill \\ \psi_{2} \left( {x - \delta x,y + \delta y,z = 0} \right) = J_{0} \left( {k_{\rho } \sqrt {(x - \delta x)^{2} + (y + \delta y)^{2} } } \right) \hfill \\ \psi_{3} \left( {x + \delta x,y - \delta y,z = 0} \right) = J_{0} \left( {k_{\rho } \sqrt {(x + \delta x)^{2} + (y - \delta y)^{2} } } \right) \hfill \\ \psi_{4} \left( {x - \delta x,y - \delta y,z = 0} \right) = J_{0} \left( {k_{\rho } \sqrt {(x - \delta x)^{2} + (y - \delta y)^{2} } } \right) \hfill \\ \end{aligned}$$

(10)

Using the setup of Fig. 1b and the same parameters as the first case (Fig. 3), but spatially displaced from the center of coordinates $\left( {\delta x;\delta y} \right)\delta x = \delta y = 1\; {\text{mm}}$, the non-diffracting beam array formed by four zero-order Bessel beams is obtained, Fig. 6.

Fig. 6

Optical reconstruction of a matrix with four zero-order Bessel beams using the SLM, with one hologram and four holograms using photorefractive holography in different positions along the propagation in z = 5, 20, 35, and 50 cm

Based on the record-reading process of photorefractive holograms, it is possible to register multiple holograms in the crystal over time, and reconstruct them in a single reading process. In this case, different holograms are recorded under the same conditions. However, an inherent effect with photorefractive materials such as BSO is the erasure of the recorded holograms while new holograms are recorded by varying the diffraction efficiency and consequently resulting in non-uniform intensity beams. One solution is to record holograms in short time intervals so that the diffraction efficiency of the new holograms accompanies the decay of the first holograms. This approach is called sequential generation and was proposed by Burke [27], who obtained a sequence of 18 holograms recorded with a constant diffraction efficiency.

In Fig. 6 are shown the transverse patterns of the beams along the propagation into the optical reconstruction of an array with four zero-order Bessel beams using the setup of Fig. 1b, where four beams spatially displaced are sequentially recorded in the crystal and each Bessel beam is with a given time interval t_i, with one hologram and four holograms using photorefractive holography in different positions along the propagation in z = 5 cm, 20 cm, 35 cm, 50 cm.

Parameters such as intensity of reference and object beams and polarizations identical to those cited above for photorefractive holography in real time were used. Figure 7 shows a graph with the evolution of the diffracted intensity by the holographic grating related to the recording of each hologram. In this case, each recorded beam process erased the previously written, due to the laser incidence on the refractive index grating; therefore, it was necessary that the decay time of the four beams was in synchrony with that in the matrix reconstruction process, then the intensity of the beam decays with the same rate.

Fig. 7

Sequential recording process of holograms for t ₁ = 19 s, t ₂ = 11.5 s, t ₃ = 9 s, and t ₄ = 6.5 s

3.3 Optical reconstruction of Frozen waves via photorefractive holography

The following is the most interesting case of this work, where the photorefractive holography was used to generate Frozen waves [10, 11, 15–17]. Considering the possibility of sequential generation of holograms using photorefractive holography, the superposition of zero-order Bessel beams co-propagating in photorefractive crystal was recorded to obtain a longitudinal pattern of specific intensity. Using the FWs given by Eqs. (5) and (6), and using

$$F(z) = \left\{ {\begin{array}{*{20}c} {1,\begin{array}{*{20}c} {} & {l_{1} \le z \le l_{2} } \\ \end{array} } \\ {0,\begin{array}{*{20}c} {} & {\text{elsewhere}} \\ \end{array} } \\ \end{array} } \right.$$

(11)

where l ₁ = 10 cm and l ₂ = 22 cm, and L = 40 cm.

For Q = 0.99999 $\omega /c$, we have N _max = 7; however, due to experimental limitations N = 2 was adopted, so that the beam spot is $\Delta \rho = 43 \mu {\text{m}}$. After determining the values of A _n , $k_{\rho n}$ and k _zn , the terms of the sum were separated (superposition) getting five fields $\varPsi_{\nu } \left( {\rho ,\phi ,\zeta } \right)$ with n = 0, 1,…, 5.

It was generated an individual CGH for each Bessel beam of the superposition, and then these were experimentally generated (object beam); next, using the sequential generation of holograms described above, the PRC crystal (holographic recording medium) was exposed to the pattern of each object beam and reference beam by a time interval given by the graph of Fig. 6. This time, the recorded beams were superimposed, resulting in sequential photorefractive holograms. The exposure times of each beam were t ₁ = 19 s, t ₂ = 11.5 s, t ₃ = 9 s, t ₄ = 6.5 s, and t ₅ = 4 s. After recording the five holograms, the object beam was blocked and only the reference beam was focused on the crystal making the simultaneous reading of the holograms; hence, the diffracted beam reconstructs the expected FW by the superposition of these Bessel beams. The results are shown in Fig. 8.

Fig. 8

a Longitudinal intensity pattern for the FW described by Eqs. (5) and (11), together with its corresponding orthogonal projections; compared to the reconstruction of FW using one and five holograms and transverse patterns in the maximum intensity position to b Eq. (5), c one hologram, and d five holograms

Similarly, another example of longitudinal shape is given by the function:

$$F(z) = \left\{ {\begin{array}{*{20}c} {1,\begin{array}{*{20}c} {} & {l_{1} \le z \le l_{2} } \\ \end{array} } \\ {1,\begin{array}{*{20}c} {} & {l_{3} \le z \le l_{4} } \\ \end{array} } \\ {0,\begin{array}{*{20}c} {} & {\text{elsewhere}} \\ \end{array} } \\ \end{array} } \right.$$

(12)

where l ₁ = 5 cm, l ₂ = 16 cm, l ₃ = 26 cm, l ₄ = 37 cm, and L = 40 cm and we obtain the experimental generation of the corresponding FW, as shown in Fig. 9, with an excellent result when compared to the theoretical solution.

Fig. 9

a Longitudinal intensity pattern for the FW described by Eqs. (5) and (12), together with its corresponding orthogonal projections; compared to the reconstruction of FW using one and five holograms and transverse patterns in the maximum intensity position to b, e, Eq. (5); c, f, one hologram; d, g, five holograms

4 Conclusions

The use of photorefractive holography to generate non-diffracting beams was effective, as presented in the results, and shows promise with generating arrays of non-diffracting beams and superposition of non-diffracting beams, where the recording and reconstruction of beams are exclusively optical. To our knowledge, it is the first time that non-diffracting beams are optically reconstructed via photorefractive holography. Therefore, the originality of this work is on recording and reconstruction of non-diffracting beams via photorefractive holography, using photorefractive holography in real time, with the record-reading process occurring almost simultaneously. This is due the high-resolution and high-speed record presented by this holographic recording medium, photorefractive BSO crystal.

Another advantage of generating non-diffracting beams using the photorefractive holography is the possibility of the direct generation of the beam without the need of the SLM and 4-f system. Besides having far superior resolution to any SLM display, its limitation is only the standard light resolution used to record the hologram, in this case, the diffraction limit of the light. Additionally, the photorefractive crystal can be used in environments that are dangerous (gas, water vapor, liquids and others) for electronic devices or for traditional holographic films.

More interestingly, the PRH resulted in beams having the same non-diffracting properties obtained with the computational holography and predicted theoretically. This means that photorefractive holography preserves the information of the non-diffracting beams and affords new possibilities of experimental generation of non-diffracting beams and/or non-diffracting beam arrays. The most interesting goals of this work were the use of photorefractive holography to generate Frozen waves. These open exciting possibilities for generating many further potentially interesting non-diffracting beams for scientific and technological applications, such as optical micromanipulation, plasma physics, optical microscopy and optics communications.