Investigation on third-order nonlinear optical properties of undoped LiNbO₃ by modified Z-scan technique

Abstract

A new method for measuring third-order nonlinear optical properties of photo refractive materials based on modified Z-scan technique in which employing focus-tunable lens was proposed. By this method, the nonlinear refractive index and the nonlinear absorption coefficient of an undoped ${\text{LiNb}}{{\text{O}}_{\text{3}}}$ crystal were investigated $\gamma = - 1.48 \times {10^{ - 12}}\;{{\text{m}}^{\text{2}}}{\text{/W}}$ and $\beta = 0.33\;{\text{mm/W}}$, respectively. The investigation suggests that the calculated results keep agreement with the traditional Z-scan technique in the order of magnitude.

1 Introduction

Nonlinear refractive index and nonlinear absorption coefficient are very important properties to research the nonlinear optical material [1–3]. Under the action of a high intensity laser, the refractive index of a nonlinear optical medium is associated with incident light intensity [4], and inside the material, the refractive index is no longer a constant. In addition, there are plentiful techniques for the measurement of nonlinear refraction in materials, for instance, degenerate four-wave mixing [5], nonlinear interferometry [6], beam distortion measurements [7], ellipse rotation [8], and nearly degenerate three-wave mixing [2]. However, the Z-scan technique [9, 10] is more general and has higher sensitivity. In addition, in recent years, a variety of improved Z-scan technologies have developed [11–17], and they also greatly improved the sensitivity of measurement. In the traditional Z-scan technique, the convergent lens is fixed, and the sample was moved along the z-axis by precision mechanical device. However, some of potential researches in the traditional Z-scan technique are limited partly, such as research of the present of the nonlinear optical parameters under different temperatures and voltages, because that the sample needs to be connected with the external specific devices which are un-moved. In views of this shortage, Radoslaw Kolkowski et al. [10] proposed a modified Z-scan technique using focus-tunable lens. Although the work is fairly perfect, they did not change the radius of the aperture accordingly which it may induce measuring errors. Because that in the traditional Z-scan technique, the beam radius in aperture plane is fixed, but in modified Z-scan technique by focus-tunable lens, it is the beam radius ${\omega _f}$ in aperture plane is variable with the change of the focal length, and the detector would accepted extra intensity when the focal length increases. In this paper, a modified Z-scan technique was proposed, in which the sample is fixed but the position of focus point is changed. In addition, we also realized that the radius of aperture should also be changed with different focal lengths.

2 Theory analysis

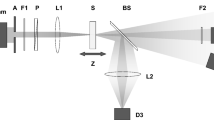
In this paper, a new method of measuring the nonlinear parameters combine with the traditional Z-scan technique is proposed in which accomplishing the measurement by employing a focus-tunable lens and adjusting the radius of apertures with the move of focus point, and the schematic diagram is shown in Fig. 1.

Fig. 1

Schematic illustration of the geometrical parameters in closed aperture Z-scan configuration. ${r_f}$ is the radius of the aperture. Detailed description is in the text

In the traditional Z-scan technique, the sample is moved along with z-axis, passing through the focus point at $z = 0$, which is located at fixed distance ƒ from the lens and at fixed distance $d$ from the aperture plane. In our research, the position of the sample is fixed, i.e., both the distance $m$ and $l$ are constants. As the focal length ƒ changes, the focus point moves along with z-axis. This leads to the variation $d$ and the variation of the relative position z of the sample with respect to the focus point which is equal to $z = m - f$. In addition, ${\omega _0}$ (beam waist) which is the beam radius at the focus point is also affected by the variation of ƒ. In the traditional Z-scan technique, ${\omega _0}$ is constant, but in our research, it changes as a linear function of ƒ:

$${\omega _0}( f) = \frac{{4f}}{{kD}}$$

(1)

where $k = 2\pi /\lambda$ is the wave vector, $\lambda$ is the laser wavelength, and $D$ is the diameter of incident beam in front of the focus-tunable lens. Note that in both Z-scan and our work, the relative position of the sample with respect to the focus point z is a variable. Therefore, the curves of both Z-scan and our research can be plotted versus z and directly compared.

For a cubic nonlinearity, the index of refraction is expressed in terms of nonlinear indices ${n_2}(esu)$ or $\gamma \;{\text{(}}{{\text{m}}^{\text{2}}}{\text{/W)}}$ through [18]:

$$n = {n_0} + \frac{{{n_2}}}{2}|E{|^2} = {n_0} + \Delta n{\text{ = }}{n_0} + \gamma I$$

(2)

where ${n_0}$ is the linear index of refraction, $E$ is the optical field, and $I$ is the radiation optical intensity. Assuming a Gaussian beam traveling in the +z direction, we can write the magnitude of $E$ as

$${E_{in}}{\text{(}}z,r,t{\text{) = }}{E_0}(t)\frac{{{\omega _0}}}{{\omega (z)}} \cdot \exp \left( - \frac{{{r^2}}}{{{\omega ^2}(z)}}\right) \cdot \exp [i\phi (z,t)]$$

(3)

However, in our research, $z = m - f$ (f is focal length of lens and it is a variation) which can be obtained from Fig. 1. Therefore, we can replace z by $m - f$ in Eq. (3) as follows:

$${E_{in}}{\text{(}}f,r,t{\text{) = }}{E_0}(t)\frac{{{\omega _0}(f)}}{{\omega (f)}} \cdot \exp \left( - \frac{{{r^2}}}{{{\omega ^2}(f)}}\right) \cdot \exp [i\phi [f,t]]$$

(4)

where ${E_0}$ indicates the radiation optical field at the focus. $\phi (f,t)$ is the wave phase factor, ${\omega ^2}(z) = {\omega _0}^2[1 + {(z/z0)]^2}$ is the beam radius at z, and it can also be written as

$${\omega ^2}(f) = {\omega _0}^2(f) \cdot [1 + {((m - f)/{f_0}_{(f = m)})]^2}$$

(5)

where ${f_0}(f = m) = k \cdot ({\omega _0}^2(m)/2)$ is the diffraction length when $f = m$. When the thickness of the sample $({l_s} \ll {f_0})({f_0}(f) = k \cdot ({\omega _0}^2(f)/2)$, and in this research, ${l_s}{\text{ = }}1\;{\text{mm}}$, and the minimum of ${f_0}(f)$ is $9.2\;{\text{mm}}$), we call it the thin sample approximation, the amplitude, and nonlinear phase change within the sample which are governed by

$$\frac{{{\text{d}}\Delta \phi }}{{{\text{d}}f}} = - \frac{{2\pi }}{\lambda }\Delta n\quad \frac{{{\text{d}}|E|}}{{{\text{d}}f}} = \frac{{{\alpha _0}}}{2}|E|$$

(6)

where ${\alpha _0}$ is linear absorption rate. The phase shift $\Delta \phi$ at the exit surface of the sample is given by Eq. (6), and it changes with the incident beam radius at the relative location of sample:

$$\Delta \phi (r,f,t) = \frac{{\Delta {\phi _0}(t)}}{{1 + ({{(m{\text{ - }}f)}^2}/{f_0}^2)}} \cdot \exp \left( - \frac{{2{r^2}}}{{{\omega ^2}(f)}}\right)$$

(7)

$$\Delta {\phi _0}(t) = \frac{{2\pi }}{\lambda } \cdot \Delta {n_0}(t) \cdot \frac{{1 - {e^{ - {\alpha _0}{l_s}}}}}{{{\alpha _0}}}$$

(8)

where $\Delta {n_0}(t)$ is the refractive index variation at focus ($f = m$). The electric field at the exit surface of the sample includes the nonlinear phase distortion:

$${E_e}(f,r,t) = E(f,r,t) \cdot \exp ( - {\alpha _0}{l_s}/2) \cdot \exp [i \cdot \Delta \phi (f,r,t)]$$

(9)

According to Huygens’s principle, the normalized instantaneous power transmittance at the aperture is

$$T(f,t) = \frac{{\int_0^{{r_f}} {|{E_a}(\Delta {\phi _0},r,f,t){|^2}r{\text{d}}r} }}{{s\int_0^\infty {|{E_a}(0,r,f,t){|^2}r{\text{d}}r} }}$$

(10)

where ${r_f} = {r_0}[1 + (m - f)/l$ is the radius of the aperture with different focal lengths, ${r_0}$ is the radius of the aperture when$f = m$,$s$ is the aperture transmittance in the linear regime. $s = 1 - \exp ( - 2{r_f}^2/{\omega _f}^2)$, $s \approx {r_f}^2/{\omega _f}^2$, where ${\omega _f}$ is beam radius in the aperture plane. The value of $\gamma$ would be get by the experimental data fitting with Eq. (10). However, the available research [18] suggested that $\gamma$ can be gained simply by numerical calculation without data fitting.

Defining that $\Delta {T_{P - V}} = {T_P} - {T_V}$ is the difference between the peak and valley of the normalized transmittance measured by Z-scan technique and it is almost relied on $\Delta {\phi _0}$ linearly, and when $s \approx 0$

$$\Delta {T_{P - V}} \approx 0.405|\Delta {\phi _0}|\quad {\text{for}}\quad |\Delta {\phi _0}| \leqslant \pi$$

(11)

From Eqs. (8) and (11), we can conclude that

$$\Delta {n_0}(t) = \frac{{\Delta {\phi _0}(t)\lambda {\alpha _0}}}{{2\pi (1 - {e^{ - {\alpha _0}{l_s}}})}} = \frac{{\Delta {T_{P - V}}\lambda {\alpha _0}}}{{0.81\pi (1 - {e^{ - {\alpha _0}{l_s}}})}}.$$

(12)

Therefore, as long as the value of $\Delta {T_{P - V}}$ would be measured by Z-scan technique, the quantity of $\gamma$ at focus would be obtained by Eqs. (2) and (12).

3 Experiment

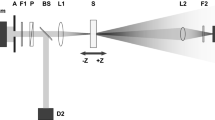
Figure 2 shows the schematic diagram of our experiment setup. A piece of poled sample of undoped pure LiNbO₃ (the biggest electro-optic coefficient ${\gamma _{33}} = 33\;{\text{pm/V}}$ and the refractive index ${n_0} = 2.323$, ${n_e} = 2.234$) was cut into a rectangle 11.5 × 13.5 × 1.0 (mm³) with the short dimension along the crystallographic c-axis (also the light path). A Gaussian beam from a semiconductor laser ($\lambda = 0.532\;\upmu{\text{m}},$ output power $\approx 10\;{\text{mW}}$) is divided by a beam splitter BS₁. Part of the beam is measured by detector D₁ as a reference in case of strong power fluctuations. The rest of the light beam incidents into the lens L (ƒ changing range from +100 to +70 mm). The focused beam is transmitted into the sample and then splitted into closed aperture and open aperture arms, where it is measured by detectors D₃ and D_2, respectively.

Fig. 2

Schematic of the modified Z-scan experimental setup: BS₁, BS₂ Beam splitter; L Focus-tunable lens; L₁ Common converging lens; D₁, D₂, D₃ Detector (an optical power and energy meter PM300E)

In the experiment, the diameter of the beam before the lens L is D = 0.6 mm, and the radius of the aperture is variable with different focal lengths of L according to ${r_f} = {r_0}[1 + (m - f)/l$ (shown in Fig. 3). Setting m = 85 mm and the ƒ changes from 100 to 70 mm, i.e., the according position of sample z changes from −15 to +15. Assuming that ${r_f}{\text{ = }}{r_0} = 1\;{\text{mm}}$ when ƒ = m = 85 mm, i.e., the focal length is equal to the distance between the coverage lens and the sample.

Fig. 3

Relation between ${r_f}$ (the radius of apertures) and ƒ (focal length of different lens), ${r_f} = {r_0}[1 + (m - f)/l]$

As the focal length changes from 100 to 70 mm, the radius of the aperture ${r_f}$ changes from 0.95 to 1.05 mm. So that the disparity result from the difference of ${\omega _f}$ (beam radius in aperture plane) can be modified.

The measuring method is modified partially by adjusting the radius of aperture. However, there is another factor that would influence the experimental outcome, i.e., the beam waist ${\omega _0}( f) = 4f/\kappa D$ (shown in Fig. 4). Therefore, the experimental data should also be multiplying by $\frac{{{\omega _0}( f\;{\text{ = }}\;{\text{m}}\;{\text{ = }}\;85)}}{{{\omega _0}( f)}}$ or $\frac{m}{f}$.

Fig. 4

Relation between ${\omega _0}( f)$ (beam waist) and ƒ

Figure 5 shows the Z-scan curves modified with ${r_f}$ and ${\omega _0}(f)$. Fig. 5a presents the open modified Z-scan curves (s = 1), and it is symmetrical relative to the focus (z = 0), and presents the maximum transmittance at z = 0. This is due to the existence of the two-photon absorption. For samples of saturated absorption, there is a maximum transmittance at z = 0. From Fig. 5a, the nonlinear absorption coefficient would be calculated $\beta = 0.33\;{\text{mm/W}}$. From Fig. 5b, the closed aperture curve, we can observe that it is no longer symmetrical about z = 0, but the modified Z-scan curve of pure refractive index change in Fig. 5c is balanced about z = 0, and the peak-to-valley configuration is indicative of a negative (self-defocusing) nonlinearity. The solid curve in Fig. 5c is the calculated result using $\Delta {\phi _0} = - 0.5,$ which gives an index change of $\gamma = - 1.48 \times {10^{ - 12}}\;{{\text{m}}^{\text{2}}}{\text{/W}}$.

Fig. 5

a Calculated open aperture curves. b Calculated closed aperture curves. c Measured Z-scan curve of a 1 mm-thick LiNbO₃ with λ = 532 nm. The solid curve is the calculated result with $\Delta {\phi _0} = - 0.5$

4 Summary

In summary, a new measurement method of third-order nonlinear parameters is proposed in which it adjust the radius of apertures according to different focal lengths. The advantages of this method are that the sample could be keep still, and the nonlinear refractive index and the nonlinear absorption coefficient of undoped LiNbO₃ are $\gamma = - 1.48 \times {10^{ - 12}}\;{{\text{m}}^{\text{2}}}{\text{/W}}$ and $\beta = 0.33\;{\text{mm/W}}$, respectively. The results obtained by this method are consistent with the traditional Z-scan technique.