1 Introduction

Microdisk and other thin semiconductor, dye-doped polymer, and erbium-doped crystalline microcavity lasers are now the objects of intensive research [1–12] as promising miniature sources of light for new generation of optical networks. As known, they can have very low lasing thresholds and their working modes (whispering-gallery modes, WGM) emit light mostly in the disk plane. Frequently the pumping is done using a wide optical beam that allows considering the cavity as fully active; however, a focused beam or the injection pumping from electrodes results in shaped active regions. Effects related to partial pumping have been studied experimentally in [13–17] where shaped electrodes and focused pump spots were used. Still such effects remain poorly studied from the side of the modeling, apparently because of the lack of adequate theoretical model. To bridge this gap, we use the lasing eigenvalue problem (LEP) [2, 18].

Determining the electromagnetic field in the presence of finite-thickness dielectric disk is a difficult 3-D problem. Still if the disk is optically thin, this problem can be reduced to 2-D analysis in the disk plane, at the expense of replacing its bulk refractive index with effective value [1–3]. Our preceding research into the modes of 2-D models of microdisks with ring-like active regions showed interesting effects related to the behavior of mode thresholds in dependence of the ring width [19, 20]. In this paper, we clarify the behavior of mode thresholds in dependence of the ring position in comparison to previously obtained solutions for fully active resonators [18] and use optical theorem [21] to explain the results.

2 Formulation and basic equations

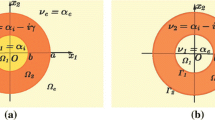
Following [13, 14] we consider the LEP formulation for a 2-D circular microcavity with a ring-like active region, which is concentric with the cavity (see Fig. 1 where active ring is highlighted with yellow filling).

Fig. 1
figure 1

Geometry of a circular microcavity with a ring-like active region

Full size image

To model the lasing, we assume that the active region material has negative imaginary part corresponding to gain and the electromagnetic field is time harmonic \(\sim\exp ( - ikct)\), \(k > 0\) and hence non-attenuating in time (c stands for the free-space velocity of light). Each point in the plane of cavity is specified by the radial and the azimuth coordinates: \(r\) and \(\phi\). In 2-D case, the field can be characterized by means of a scalar function \(u\), which is the  \(E_{z}\) or  \(H_{z}\) component depending on the polarization. This function must satisfy the Helmholtz equation

$$\Delta u + k_{j}^{2} u = 0,\quad x \in \varOmega_{j} ,\;j = 1,\,2,\,3,\,e,$$
(1)

off the boundaries, the transmission conditions

$$u^{ - } = u^{ + } ,\quad \eta_{j} \frac{{\partial u^{ - } }}{\partial n} = \eta_{j + 1} \frac{{\partial u^{ + } }}{\partial n},\quad x \in \varGamma_{j} ,\;j = 1,\,2,\,3,$$
(2)

at the boundaries, and Sommerfeld radiation condition at infinity. Here \(k_{j} = k\nu_{j}\), \(\eta_{j} = \nu_{j}^{ - 2}\) in the H-polarization case and \(\eta_{j} = 1\) in the E-polarization case, \(j = 1,\;2,\;3,\;e\), \(\nu_{1,3} = \alpha_{i}\), \(\nu_{2} = \alpha_{i} - i\gamma \;\;(\gamma > 0)\), \(\nu_{4} = \nu_{e} = \alpha_{e}\), and \(u^{ \pm } = u(r \pm 0,\phi )\), \(r = r_{1} ,\;r_{2} ,\;r_{3}\).

We look for the LEP eigenvalues as discrete pairs of the real-valued parameters \((\kappa_{N} ,\gamma_{N} )\). Here \(\kappa_{N} = k_{N} r_{3}\) is the normalized frequency of lasing, \(\gamma_{N} > 0\) is the threshold material gain, and N is the generalized mode index. Note that the threshold gain per unit length, common in the analysis of Fabry–Perot lasers, can be easily calculated as \(g = k\gamma\).

The LEP problem (1)–(2) is treated with the method of separation of variables. All modes split into independent families according to the azimuth index m. For every m, the eigenvalues \((\kappa ,\gamma )\) satisfy the following characteristic equation:

$$\left| {\begin{array}{*{20}c} {K_{1}^{(1,1)} } & {K_{1}^{(1,3)} } & {K_{1}^{(1,4)} } & 0 & 0 & 0 \\ {K_{1}^{(2,1)} } & {K_{1}^{(2,3)} } & {K_{1}^{(2,4)} } & 0 & 0 & 0 \\ 0 & {K_{2}^{(1,1)} } & {K_{2}^{(1,2)} } & {K_{2}^{(1,3)} } & {K_{2}^{(1,4)} } & 0 \\ 0 & {K_{2}^{(2,1)} } & {K_{2}^{(2,2)} } & {K_{2}^{(2,3)} } & {K_{2}^{(2,4)} } & 0 \\ 0 & 0 & 0 & {K_{3}^{(1,1)} } & {K_{3}^{(1,2)} } & {K_{3}^{(1,4)} } \\ 0 & 0 & 0 & {K_{3}^{(1,1)} } & {K_{3}^{(2,2)} } & {K_{3}^{(2,4)} } \\ \end{array} } \right| = 0.$$
(3)

Here we denote,

$$\begin{aligned} K_{j}^{(1,1)} = J_{m} (k_{j} r_{j} ),\quad K_{j}^{(1,2)} = H_{m}^{(1)} (k_{j} r_{j} ),\quad K_{j}^{(2,1)} = \eta_{j} k_{j} J^{\prime}_{m} (k_{j} r_{j} ),\quad K_{j}^{(2,2)} = \eta_{j} k_{j} H_{m}^{{(1)^{\prime}}} (k_{j} r_{j} ),\; \\ K_{j}^{(1,3)} = - J_{m} (k_{j + 1} r_{j} ),\quad K_{j}^{(1,4)} = - H_{m}^{(1)} (k_{j + 1} r_{j} ),\quad K_{j}^{(2,3)} = - \eta_{j + 1} k_{j + 1} J^{\prime}_{m} (k_{j + 1} r_{j} ),\quad K_{j}^{(2,4)} = - \eta_{j + 1} k_{j + 1} H_{m}^{{(1)^{\prime}}} (k_{j + 1} r_{j} ), \\ \end{aligned}$$
(4)

where \(J_{m} (z)\) is the Bessel function and \(H_{m}^{(1)} (z)\) is the Hankel function of the first kind and index \(m = 0,1,2, \ldots\).

We use another index, \(n = 0,1,2, \ldots\), to number the eigenvalues within each m-th family. The index \(n\) characterizes the modal field variations along the radius of the microcavity. Note that in the uniformly active (e.g., flood pumped) circular cavity [18] the eigenvalues with \(n = 1\) correspond to WGMs and show the lowest thresholds, which get exponentially lower with greater \(m > > 1\).

3 Results and discussion

In the numerical analysis, we looked for the roots of (3) on a selected part of the plane \((\kappa ,\gamma )\) with the aid of in-house iterative algorithm based on the two-parametric Newton technique. We studied the H-polarized modes because in this case the effective refractive index of a thinner-than-wavelength disk is much larger than in the E-polarization case (e.g., see Appendix in [18]). As it was demonstrated in [18], this entails correspondingly higher threshold values of material gain of the WGMs.

In Figs. 2 and 3, we present the dependences of the mode threshold gains and the lasing frequencies on the relative position of the middle radius \(\rho_{{\text{mid}}} = r_{{\text{mid}}} /r_{3}\) of the active ring (a model of a ring electrode) of the width \(d = r_{2} - r_{1} = 0.1r_{3}\). In computations, we assumed that the cavity material had refractive index \(\alpha_{i} = 2.63\) and the environment was air with \(\alpha_{e} = 1\). As one can see, the frequencies of WGMs are not sensitive to the ring placement.

Fig. 2
figure 2

Dependences of the threshold material gains for the circular microcavity with a ring-like active region on the middle radius of the ring \(\rho_{{\text{mid}}}\). The minimum values of threshold gains are marked with crosses. The threshold gains of the corresponding modes for the fully active circular microcavity are marked with dots

Full size image
Fig. 3
figure 3

Same as in Fig. 2 for the lasing frequencies. The values of \(\rho_{{\text{mid}}}\) corresponding to the minima of the threshold gains are marked with crosses. The normalized frequencies of lasing of the same modes of the fully active circular microcavity are marked with circles

Full size image

In contrast, the thresholds show that the electrode must be placed at a certain distance from the rim of the cavity and, if \(\rho_{{\text{mid}}}\) gets smaller, then the WGM thresholds grow up exponentially.

This behavior of mode thresholds can be understood using the optical theorem for lasers [21]. Here, the most important role is played by the overlap coefficient, \(\varGamma_{N}^{(a)} = \tilde{W}_{N}^{(a)} /\tilde{W}_{N}\), i.e., the fraction of the E-field power contained in the active region \(\varOmega_{2}\) relatively to the power in the whole cavity volume, \(\varOmega = \varOmega_{1} + \varOmega_{2} + \varOmega_{3}\). This is a discrete quantity linked to specific modes. According to the results of [21], if \(\gamma_{N} < < 1\) then \(\gamma_{N} = \alpha_{i} Q_{N} /\varGamma_{N}^{(a)} + O(\gamma_{N}^{2} )\), where \(Q_{N}\) is the quality factor of the N-th mode of passive cavity, i.e., the same cavity without pumping (note that \(Q_{N}\) does not depend, by definition, on the active region size and location). For the considered here circular microcavity with a ring-like active region, the values of \(\tilde{W}_{N}^{(a)}\) and \(\tilde{W}_{N}\) take the form as

$$\tilde{W}_{N}^{(a)} (k_{N} ,\gamma_{N} ) = (1/2Z_{0} )(\alpha_{i}^{2} - \gamma_{N}^{2} )\int_{{\varOmega_{2} }} {|u(r,\phi ;} \;k_{N} ,\gamma_{N} )|^{2} rdrd\phi ,$$
(5)
$$\tilde{W}_{N} (k_{N} ,\gamma_{N} ) = (1/2Z_{0} )\int_{\varOmega } {\text{Re} (\nu^{2} )|u(r,\phi ;} \;k_{N} ,\gamma_{N} )|^{2} rdrd\phi ,$$
(6)

where \(Z_{0} = (\mu_{0} /\varepsilon_{0} )^{1/2}\) is the free-space impedance.

Figure 4 shows the dependences of the threshold gains (top panels) and the overlap coefficients (middle panels) on \(\rho_{{\text{mid}}}\) for the H-polarized WGMs with m = 20 and n = 1,2,3, respectively, of the circular microcavity with a ring-like active region of the width \(d = 0.1r_{3}\). The minimum values of the threshold gains and the maximum values of the overlap coefficients are marked with crosses. The threshold gains of the same modes for the fully active circular microcavity are marked with the circles in the top panel. We see that the \(\rho_{{\text{mid}}}\) values providing the minima of the threshold material gains graphically coincide with those corresponding to the maxima of the overlap coefficients, as predicted by the optical theorem for LEP, since for these modes \(\gamma_{s} < 10^{ - 3}\).

Fig. 4
figure 4

Dependences of the threshold material gains (top panel) and the overlap coefficients (bottom panel) on \(\rho_{{\text{mid}}}\) for WGMs (20,1), (20,2) and (20,3) of the circular microcavity with the ring-like active region of the width \(d = 0.1r_{3}\). The maxima of the overlap coefficients and the minima of the threshold gain are marked with crosses. The threshold gains of the same modes for the fully active circular cavity are indicated with the dots in the top panel

Full size image

The gain profiles and the modal fields corresponding to the minima of threshold gains in Fig. 4 of the same three WGMs in the same circular microcavity are presented in Fig. 5. As one can see, the threshold minima and the overlap coefficients maxima are obtained when the maximal fractions of the E-field power are contained in the active region.

Fig. 5
figure 5

From top to bottom: the gain profiles (yellow boxes) and the modal field profiles (color curves) for WGMs (20,1), (20,2) and (20,3) of the microcavity with the same parameters as in Fig. 4, in the minima of threshold material gain dependences

Full size image

Here, we emphasize that new finding is that the optimal placement of the active ring (i.e., the electrode) is not along the rim but at a certain distance inward from it. This distance corresponds to the inward shift of the most intensive E-field maximum and hence is dictated by the type of the working mode.

Consider now the circular microcavity with the ring-like active region of the width \(d = 0.1r_{3}\) and the middle radius \(r_{mid} = 0.9r_{3}\) (hence, \(r_{1} = 0.85r_{3}\) and \(r_{2} = 0.95r_{3}\)). Figure 6 demonstrates, on the plane \((\kappa ,\gamma )\) where \(\gamma\) is presented in logarithmic scale, the normalized frequencies of lasing and the corresponding values of threshold material gain for all H-polarized WGMs with m from 1 to 30 and n = 1,2,3. They are shown, for comparison, together with the LEP eigenvalues of the same WGMs of the fully active circular microcavity.

Fig. 6
figure 6

Normalized frequencies of lasing and the threshold gains for the WGMs of the circular microcavity with a ring-like active region of the width \(d = 0.1r_{3}\) and the middle radius \(r_{{\text{mid}}} = 0.9r_{3}\) (×crosses) in comparison to the same values for a fully active circular cavity (∙ dots) and a cavity with losses introduced in the passive regions \(\varOmega_{1}\) and \(\varOmega_{3}\) as \(\nu_{1,3} = \alpha_{i} + i10^{ - 8}\) (+crosses)

Full size image

From Fig. 6, we see that, by using a ring-like active region to pump such a microcavity, one can considerably modify the localization of the LEP eigenvalues. For instance, in the interval of frequencies \(5.9 < \kappa = kr_{3} < 6.9\), the solutions with radial index n = 2 having the material thresholds \(\gamma < 0.01\) exist in the fully active circular microcavity and do not exist in the microcavity with the ring-like active region of \(d = 0.1r_{3}\) and \(r_{{\text{mid}}} = 0.9r_{3}\). Note that normally this has been achieved by replacing the solid circular microdisk with a microring [20]. However, from the presented above analysis it follows that the same effect can be obtained by manipulating the electrode width and radial location only.

For clarity, we show, also in Fig. 6, the effect of losses present in the passive parts of the microcavity. Such losses remain, for instance, due to the inter-band transitions in the material of un-pumped active region. As one can see, the presence of absorption in the passive regions characterized with \(\text{Im} \nu_{1,3} > 0\) spoils the thresholds of all WGMs, which had \(\gamma < \text{Im} \nu_{1,3}\) in the lossless cavities. This is understandable because in that case, to achieve the lasing, the total gain in the cavity must balance not only the radiation losses, decreasing with mode’s azimuth index m, but also the absorption losses, which have the order of \(\text{Im} \nu_{1,3}\) independently of the mode indices (see Eq. (36) in [21]).

For the sake of completeness, we would like to add that there are a few other LEP-like formulations extracting the thresholds of lasing—see [22–27]. Here, the authors of [27] followed the LEP as above, and works [22] and [23] used only a different (within a factor) definition of the material threshold. Still we would like to stress that the LEP is based entirely on Maxwell equations with exact boundary conditions and radiation condition at infinity. It is equally rigorous in the analysis of low-threshold and high-threshold lasing modes. We believe that the demonstrated power of LEP to predict the dynamics of mode thresholds based on the mode-active-region overlap coefficients and the optical theorem makes it an important instrument in electromagnetic analysis and computer-aided optimization of various lasers.

4 Conclusions

We have studied the behavior of spectra and thresholds of WGMs of circular microcavity lasers with ring-like active regions (e.g., ring electrodes) under variation of ring location and width, in 2-D formulation. We have demonstrated that the dynamics of the lasing mode thresholds in the cavities can be excellently explained with the aid of overlap coefficients between the modal E-field and the active region. Here, we have found that, for each mode, the optimal position of the active ring must be shifted inward from the rim to overlap with the strongest E-field maximum. Our analysis has also shown that a judicious choice of the combination of active ring width and location can efficiently remove the higher radial-index modes from the working interval of frequencies.