1 Introduction

Optical parametric amplifiers (OPAs) have been developing since the first solid laser was invented in the early 1960s. Until the 1980s, the development of novel efficient nonlinear crystals and improvement of pump lasers meant that OPA had been one effective way to achieve laser pulses with new wavelengths. This met the increasing demands for ultrashort laser pulses at new wavelengths and compensated for the lack of proper lasing media. As a result, extensive research was conducted into OPAs [1–3]. In addition, its advantages such as high-gain and high-contrast mean that OPA could serve as the seed source or preamplifier in high-power laser systems [4–6]. However, it is not sufficient to have only the aforementioned high-gain and high-contrast for the seed source or the preamplifier. The laser beam quality also plays an important role in the subsequent amplification processes and high-field physics experiments. We are often concerned with the far-field beam quality, because the laser pulse intensity and the spatial resolution can be dramatically improved by focusing [7, 8]. Achieving high intensity and resolution is important for the generation of high-energy electron beams and for microimaging [9, 10]. However, the focusing process often causes astigmatism [11, 12], which will deteriorate the beam quality, laser intensity, and spatial resolution. Moreover, in coherent combining and other similar processes, the existing astigmatism may destroy the spatial coherence, and this will lead to poor synthesis quality [13]. Therefore, reducing or eliminating astigmatism is essential for the application of OPA sources [14–16], and the factors that affect the astigmatism properties of the output pulses of OPA should be studied.

Many efforts have been made to research and improve the beam quality of OPAs. Guardalben et al. [17] investigated the influence of saturated gain on the beam quality in OPA; they also pointed out that spatial walk-off between the pump and signal beam can further reshape the latter beam in the OPA process. Wei et al. [18] theoretically analyzed the pump-to-signal phase transfer caused by walk-off effects. They found that modulation in the input pump beam could be transferred into the signal beam owing to the spatial walk-off in the OPA process. In 2010, Farsund pointed out that the spatial walk-off may lead to asymmetry of the output signal beam in the parametric amplification process [19], and we think this asymmetry may invoke astigmatism in OPA. These previous studies have investigated many characteristics of beam quality in OPA; however, as one of the most common aberrations in the focusing process, astigmatism in OPA has not yet been studied.

In this paper, we study the astigmatism characteristics in an OPA process. We numerically simulate the OPA process using the coupled second-order three-wave nonlinear equations. Taking into account the possible influence of spatial walk-off [17], we numerically compare three cases with different polarizations or pump pulse astigmatism. We find that the astigmatism is predominantly transferred from the pump to the idler beam. In addition, we analyze the influence of pump energy on the astigmatism transfer process.

We also experimentally researched this process to verify the simulations. This presents an obvious result that the astigmatism will be transferred from the pump into the idler beam, and this result is in good agreement with the analytical and numerical conclusions. According to these results, we suggest that pump pulse astigmatism should be eliminated to avoid astigmatism of the idler. As we know, both signal and idler are feasible candidates for subsequent application processes because they can both be tuned and have high temporal contrast. It is also noteworthy that the temporal contrast depends on the gain, so we often choose the idler beam to achieve a better temporal contrast. However, the astigmatism existing in the idler beam is a negative factor for applications. We believe this investigation on astigmatism phenomenon in OPA process can provide some clues for the design of ultrashort laser sources.

2 Theoretical analysis

To analyze the astigmatism transfer mechanism in optical parametric amplification, we start with the coupled differential equations. We adopt the equations in the Fourier space from [20]

$$\begin{aligned} \frac{{\partial E_{s} \left( {k_{x} ,k_{y} ,z} \right)}}{\partial z} = ik_{s,z} \left( {k_{x} ,k_{y} } \right)E_{s} \left( {k_{x} ,k_{y} ,z} \right) + \frac{{i\mu_{0} \omega_{s} c}}{{2n_{s} }}F\left( {P_{s} \left( {x,y} \right)} \right) \hfill \\ \frac{{\partial E_{i} \left( {k_{x} ,k_{y} ,z} \right)}}{\partial z} = ik_{i,z} \left( {k_{x} ,k_{y} } \right)E_{i} \left( {k_{x} ,k_{y} ,z} \right) + \frac{{i\mu_{0} \omega_{i} c}}{{2n_{i} }}F\left( {P_{i} \left( {x,y} \right)} \right) \hfill \\ \frac{{\partial E_{p} \left( {k_{x} ,k_{y} ,z} \right)}}{\partial z} = ik_{p,z} \left( {k_{x} ,k_{y} } \right)E_{p} \left( {k_{x} ,k_{y} ,z} \right) + \frac{{i\mu_{0} \omega_{p} c}}{{2n_{p} }}F\left( {P_{p} \left( {x,y} \right)} \right). \hfill \\ \end{aligned}$$
(1)

Here, F is the Fourier transform, that is,

$${\text{F}}\left( {P\left( {x,y} \right)} \right) = \frac{1}{{\left( {2\pi } \right)^{2} }}\iint {{\text{d}}x{\text{d}}y\text{exp}\left[ { - i\left( {k_{x} x + k_{y} y} \right)} \right]} P\left( {x,y} \right).$$
(2)

P j is the second-order polarization at ω j caused by other beams. It is given by

$$\begin{aligned} P_{s} \left( {x,y} \right) = 2\varepsilon_{0} \chi_{{e{\text{ff}}}} E_{i} \left( {x,y} \right)^{*} E_{p} \left( {x,y} \right) \hfill \\ P_{i} \left( {x,y} \right) = 2\varepsilon_{0} \chi_{\text{eff}} E_{s} \left( {x,y} \right)^{*} E_{p} \left( {x,y} \right) \hfill \\ P_{p} \left( {x,y} \right) = 2\varepsilon_{0} \chi_{\text{eff}} E_{s} \left( {x,y} \right) E_{i} \left( {x,y} \right). \hfill \\ \end{aligned}$$
(3)

We take into account dispersion, diffraction, birefringence, and spatial and temporal walk-off effects in the calculation of \(k_{z} \left( {k_{x} ,k_{y} } \right)\) [21]. Here, \(k_{z} \left( {k_{x} ,k_{y} } \right)\) is the projection of the wavenumber in propagation direction z for a single spatial frequency. The dispersion, phase-match, and temporal (longitudinal) walk-off effects are contained in the calculation of wavenumber by \(k=n\frac{2\pi }{\lambda }\), where λ is the wavelength in a vacuum. On the other hand, the diffraction, birefringence, and spatial (transverse) walk-off effects are taken into account in the calculation of the projection of wavenumber by \(k_{\text{z}}= k\cos (\theta )\), where θ is the angle between the direction of the corresponding angular frequency and z. In addition, we ignore the absorption in Eq. (1).

In order to simplify the mathematical expression, we ignore some spatial effects, such as diffraction and spatial walk-off, and assume a constant pump field. The signal and idler evolution is given by:

$$\begin{aligned} \frac{{\partial E_{s} \left( {x,y} \right)}}{\partial z} = \frac{{2i\mu_{0} \omega_{s} c\varepsilon_{0} \chi_{{e{\text{ff}}}} }}{{2n_{s} }}E_{i} \left( {x,y} \right)^{*} E_{p} \left( {x,y} \right) \hfill \\ \frac{{\partial E_{i} \left( {x,y} \right)}}{\partial z} = \frac{{2i\mu_{0} \omega_{i} c\varepsilon_{0} \chi_{{e{\text{ff}}}} }}{{2n_{i} }}E_{s} \left( {x,y} \right)^{*} E_{p} \left( {x,y} \right). \hfill \\ \end{aligned}$$
(4)

We express the waveform as

$$E_{j} \left( {x,y} \right) = A_{j} \left( {x,y} \right){\text{e}}^{{i\phi_{j} \left( {x,y} \right)}} .$$
(5)

Here, j represents s, i, and p, standing for the signal, idler, and pump, respectively.

Then, we have

$$\begin{aligned} {\text{d}}A_{s} \left( {x,y} \right)e^{{i\phi_{s} \left( {x,y} \right)}} = - \frac{{2\mu_{0} \omega_{s} c\varepsilon_{0} \chi_{{e{\text{ff}}}} }}{{2n_{s} }}{\text{e}}^{{ - i\frac{\pi }{2}}} A_{i} \left( {x,y} \right)^{ *} {\text{e}}^{{ - i\phi_{i} \left( {x,y} \right)}} A_{p} \left( {x,y} \right){\text{e}}^{{i\phi_{p} \left( {x,y} \right)}} {\text{d}}z \hfill \\ {\text{d}}A_{i} \left( {x,y} \right)e^{{i\phi_{i} \left( {x,y} \right)}} = - \frac{{2\mu_{0} \omega_{i} c\varepsilon_{0} \chi_{\text{eff}} }}{{2n_{i} }}{\text{e}}^{{ - i\frac{\pi }{2}}} A_{s} \left( {x,y} \right)^{ *} {\text{e}}^{{ - i\phi_{s} \left( {x,y} \right)}} A_{p} \left( {x,y} \right){\text{e}}^{{i\phi_{p} \left( {x,y} \right)}} {\text{d}}z. \hfill \\ \end{aligned}$$
(6)

According to Eq. (6), the relationships of the phases are

$$\phi_{i} \left( {x,y} \right) = - \frac{\pi }{2}+\phi_{p} \left( {x,y} \right){ - }\phi_{s} \left( {x,y} \right),$$
(7)
$$\phi_{s} \left( {x,y} \right) =- \frac{\pi }{2}+\phi_{p} \left( {x,y} \right){ - }\phi_{i} \left( {x,y} \right).$$
(8)

Because the initial idler wave is zero, the phase of the generated idler is

$$\phi_{i} \left( {x,y} \right) = { - }\frac{\pi }{2}+\phi_{p0} \left( {x,y} \right){ - }\phi_{s0} \left( {x,y} \right).$$
(9)

Here, the \(\phi_{p0} \left( {x,y} \right)\) and \(\phi_{s0} \left( {x,y} \right)\) are the initial phase of pump and signal beams, respectively, and then the phase of generated signal is

$$\phi_{s} \left( {x,y} \right) = \phi_{s0} \left( {x,y} \right),$$
(10)

Equation 10 indicates that the signal beam can preserve the spatial phase in the OPA process, so that the astigmatism of the pump will not affect the signal beam. In contrast, Eq. (9) indicates that the pump spatial phase can influence astigmatism of the idler beam. In order to verify these conclusions and explicitly study the astigmatism transfer mechanism, we numerically simulated the astigmatism transfer process.

3 Simulations

In the previous section, we analytically investigated the astigmatism based on the spatial phase relationships in a relatively simple setting. When other factors, such as pump depletion, dispersion, diffraction, and spatial walk-off, are taken into consideration, the analytical results given in the previous section may be no longer valid. Hence, in this section, we use numerical simulation to investigate the details of astigmatism transfer process in OPA. The simulation model is built on Eqs. (1, 2, 3), which consider the diffraction, walk-off, and dispersion effects. We should take note that we adopted the split-step Fourier method to solve Eq. (1) in our simulations. The essential approximation for this theoretical model is that the spectral amplitudes vary slowly compared to the optical wavelength. The validity of this approximation has been proved in [22]. In this paper, we limit our theoretical study to a 2-mm-long BBO crystal and a peak pump intensity of 60 GW/cm2. The temporal resolution is 2 fs and the spatial resolution is 39 µm in the critical direction (horizontal direction, x), and the same as the noncritical (vertical direction, y) direction. After comparing to simulations with higher temporal or spatial resolution, we verify that these resolutions are sufficient to guarantee the validity of the simulations.

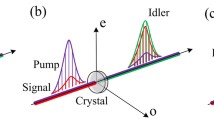
We first investigated a configuration similar to a realistic experiment (shown in Fig. 5). The seed pulse has a duration of 75 fs (FWHM), shown by the red line in Fig. 1a. It is chirped with a GDD of 700 fs2, corresponding to a stretched-pulse spectrum ranging from 1500 to 1700 nm (red line in Fig. 1b). The pump pulse has a duration of 100 fs (FWHM), shown by the blue line in Fig. 1a). It is chirped with a GDD of −1100 fs2, corresponding to a stretched-pulse spectrum ranging from 760 to 840 nm (blue line in Fig. 1b). Both the signal and pump pulses have spatial Gaussian distributions and radii (1/e2) of 5.5 and 6 mm, respectively, as shown in Fig. 1d. The energies of the input pump and signal are 4.06 mJ and 3 μJ, respectively. The BBO crystal is cut at 29° in the x–z plane for type II phase match. In the theoretical analysis, we assume that the two transverse dimensions (x and y) have the same intensity distribution and that the initial spatial phase of the signal is flat. However, the pump has different spatial phase distributions in the two transverse dimensions, as described in Fig. 1c. These phases could be caused by the telescope or other imaging system in a realistic OPA.

Fig. 1
figure 1

Initial simulation conditions. a Input temporal distribution of pump and signal pulses. b Input spectrum of pump and signal pulses. c Input spatial distribution of the phase of pump and signal beams. d Input spatial distribution of intensity of pump and signal beams

Full size image

Under the above assumptions, we simulate the evolution of three waves in the optical parametric amplification process. It should be pointed out that the input spatial phase of the pump beam is obtained by ray-tracing using the Zemax program, of a telescope similar to that in the realistic experimental setup. Based on the aforementioned conditions, we could simulate the astigmatism characteristics of the beams. We calculated beam profiles in the far-field to illustrate astigmatism. The simulation results of the input pump are shown in Fig. 2b1–b3, the beam profiles in far-field of the input signal pulse are shown in Fig. 2a1–a3, and the related output beam profiles are shown in Fig. 2c1–c3. From Fig. 2d1–d3, we find that the output idler pulse has astigmatism, but the amplified signal pulse has no astigmatism, as shown in Fig. 2c1–c3.

Fig. 2
figure 2

Simulated beam profiles. P −1 corresponds to a location 200 mm before the focal point, P 0 corresponds to the focal point, and P 1 corresponds to a location 200 mm after the focal point. Here, \(f = \frac{(a - b)}{a}\) is ellipticity, where a is the larger semi-major axis and b is the smaller semi-major axis

Full size image

We also calculated the spatial phase distributions in the horizontal and vertical directions, as shown in Fig. 3a and d. The phase distributions of the idler pulse are curved differently in the x and y directions, but the phase of the signal pulse is flat in both directions. These spatial phase distributions of the idler demonstrate that the astigmatism has appeared. For convenience, we use the spatial phase in two directions to represent astigmatism in the following simulations.

Fig. 3
figure 3

Spatial distribution of the phase of signal and idler pulses with different phase-match types or input pump spatial phase

Full size image

The spatial walk-off effect (and other spatial effects, such as birefringence and diffraction) that exists in the amplification process may also cause the astigmatism [17]. In order to clearly investigate the influences of spatial walk-off on the astigmatism, simulations are carried out in three cases with the results shown in Fig. 3. In the first case, as shown in Fig. 3a and d, the laser conditions for the simulation are the same as in Fig. 2. Considering that the birefringence may invoke the spatial walk-off, in the second case we exchange the polarization between the signal and idler beams, with the results shown in Fig. 3b and e. In comparison, we also use a pump pulse with no astigmatism in the third case and the same other parameters as in the first case, with the results shown in Fig. 3c and f.

The spatial walk-off effect can possibly cause the spherical spatial asymmetry, which causes the astigmatism. However, in the final stage of an OPA, the beam size is large enough to ignore the spatial walk-off. In the case of our simulation and following experiment, the transverse walk-off angle is about 63.89 mrad, which corresponds to 0.13-mm transverse walk-off length for a 2-mm-long crystal, and the diameter of the input signal pulse is about 11 mm, and thus, we could ignore the impact of the spatial walk-off effect. Hence, when we compare Fig. 3a and d with Fig. 3b and e, we find that type of phase match will not affect the astigmatism transfer process, and this result confirms that the astigmatism originated from walk-off is small enough. On the other hand, as shown in Fig. 3f, if the pump has no astigmatism, the output idler pulse astigmatism disappears comparing to that in Fig. 3d and e. This means that the net idler pulse astigmatism that originated from the spatial walk-off is negligible. By removing the influence of spatial walk-off, we can conclude that the astigmatism that exists in the idler beam pulse is mainly transferred from the pump beam pulse.

Because astigmatism in the idler beam is completely inherited from the pump beam, the pump intensity may influence the astigmatism transfer process. For this reason, we also change the input pump energy to observe the influence on this astigmatism transfer process. The result is shown in Fig. 4. The output pulses maintain the same astigmatism with increasing pump energy, which suggests that the change in pump energy hardly affects the astigmatism of output beams in the amplification process. In Fig. 4, we also notice that the signal has obvious quadratic phases and weak astigmatism at a pump energy of 4 mJ. After some further comparative simulations, we find that these phase profiles are similar to the distribution of output pump intensity. In our simulations, we limit the nonlinear effects to second order; therefore, we guess that the mechanism generating this strange phase is the Pockels effect. Meanwhile, in order to test and verify the simulation results, we performed a related experiment based on our lab-built OPA device.

Fig. 4
figure 4

Output spatial distribution of the phase of signal (a) and idler (b) beams with different input pump energies

Full size image

4 Experimental

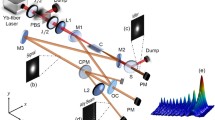
The experiment was performed with an OPA device. The astigmatism phenomena were investigated in the final amplification stage. A schematic diagram of the experimental setup is illustrated in Fig. 5. Our lab-built laser system produced the signal pulse, and the initial seed was produced by white light generation similar to that in Ref. [23]. The seed pulse had a pulse duration of ~75 fs and energy of ~3 μJ and was centered at 1600 nm. It was pumped with 1 kHz/4 mJ/100 fs laser pulses from a Ti:sapphire laser system (Astrella, Coherent). The pump beam was re-imaged by a reflective telescopic system to match the signal spot. The seed pulse and pump pulse were combined on a dichroic mirror and then transmitted to the nonlinear crystal to achieve amplification. The phase distributions of the initial input pump and signal pulses were flat, but after passing through the telescope with spherical mirrors (~7.5°) the phase distribution curve changed owing to the introduced astigmatism. The simulated phase distribution is shown in the lower portion of Fig. 5.

Fig. 5
figure 5

Diagram of the experimental setup. The NLC (nonlinear crystal). Measurement system is shown in the inset figure. The corresponding simulated phase distributions at points a, b, and c are shown in the bottom half of the figure

Full size image

To detect this astigmatism, we measured the beam profiles at three locations near the focus of a lens with a beam analyzer (SP620U, Ophir Photonics); the focal length of the lens was 1000 mm. The profiles of the input pump, output signal, and output idler pulses were measured. We separated the signal and idler beam with a small divergent angle in the noncritical direction (vertical direction). To clearly describe the effect, we chose three locations (described in Fig. 5), which were ~200 mm before the focal point (marked as point P−1), the focal point (marked as point P0), and ~200 mm after the focal point (marked as point P1).

As shown in the figure, the beam profile of the input signal has no astigmatism (Fig. 6a1–a3), and the input pump beam has obvious astigmatism (Fig. 6b1–b3) introduced by the telescope system (shown in Fig. 5). After the amplification, the measured results illustrate that the beam profile of the idler is broadened in the vertical direction at P-1 (Fig. 6d1) but broadened in the horizontal direction at P1 (Fig. 6d3). This phenomenon indicates that astigmatism exists in the generated idler beam. In contrast, there is no astigmatism in the amplified signal (Fig. 6c1–c3). These experimental results are in good agreement with the above theoretical analyses and simulations. The experimental results further confirm that the pump pulse astigmatism can be transferred into the idler beam but not into the signal beam.

Fig. 6
figure 6

Measured beam profiles of the pump, signal, and idler beam pulses; P −1/P 0/P 1 represent the detected positions as shown in Fig. 5. f is the ellipticity

Full size image

5 Conclusions

In this study, the astigmatism transfer process in OPA has been investigated both numerically and experimentally. Based on the coupled second-order three-wave nonlinear propagation equations, we have analytically and numerically verified that the astigmatism of the pump can be transferred into the idler beam but not into the signal beam. The numerical simulations also illustrate that the astigmatism transfer process is not affected by the phase-match type, spatial walk-off, or input pump energy. Meanwhile, the astigmatism transfer process is further confirmed in the experiment. As mentioned, OPA can provide laser sources with excellent performance, but the internal optics, such as the reflective telescope system, may cause astigmatism. Based on the achieved results, we propose that astigmatism can be eliminated by canceling the pump astigmatism or by adopting the signal beam for the subsequent application and that this is an effective approach to improving the beam quality of ultrafast parametric optical sources.