Frequency-comb referenced collinear laser spectroscopy of Be⁺ for nuclear structure investigations and many-body QED tests

Abstract

Transition frequencies of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2 {\text{P}}_{1/2,\,3/2}$ transitions in Be$^+$ were measured in stable and short-lived isotopes at ISOLDE (CERN) using collinear laser spectroscopy and frequency-comb-referenced dye lasers. Quasi-simultaneous measurements in copropagating and counterpropagating geometry were performed to become independent from acceleration voltage determinations for Doppler-shift corrections of the fast ion beam. Isotope shifts and fine-structure splittings were obtained from the transition frequencies measured with a frequency comb with accuracies better than 1 MHz and led to a precise determination of the nuclear charge radii of $^{7,10-12}$Be relative to the stable isotope ⁹Be. Moreover, an accurate determination of the 2p fine-structure splitting allowed a test of high-precision bound-state QED calculations in the three-electron system. Here, we describe the laser spectroscopic method in detail, including several tests that were carried out to determine or estimate systematic uncertainties. Final values from two experimental runs at ISOLDE are presented, and the results are discussed.

1 Introduction

Laser spectroscopy provides a detailed insight into atomic structure including all subtle effects that contribute to the exact energy and the splittings of individual energy levels. Many of these effects are of great relevance in fundamental physics problems, as, for example, quantum electrodynamics, nuclear structure and weak interaction. Nowadays, laser spectroscopy combined with theoretical calculations is an indispensable tool to explore many-body QED in weak and strong fields and the search for a time or spatial dependence of fundamental constants like the fine-structure constant. It provides important information for the analysis of spectra from stars and quasars, for studies of the nuclear structure and for determining the weak charge of a nucleus.

The technique we present here has provided new data in two of the mentioned fields, namely the determination of nuclear charge radii and moments of beryllium isotopes [1, 2] and the test of many-body bound-state QED calculations in three-electron systems [3]. It is based on collinear laser spectroscopy, a technique that has been contributing to these fields considerably and is one of the workhorses for investigations of nuclear spins and moments, which is witnessed by a long series of review papers [4–11] over the last decades. In parallel, it has also been used to investigate the fine-structure splittings in helium-like ions as a test of bound-state QED. Such tests were carried out using boron B$^{3+}$ [12], nitrogen N$^{5+}$ [13] and fluorine F$^{7+}$ [14]. In these experiments counter- and copropagating beams have been used to determine transition frequencies, while for the spectroscopy of short-lived neon isotopes a similar approach was used to calibrate the acceleration voltage of the ions [15, 16].

For the measurements on beryllium isotopes we have further developed this technique and combined it with a frequency comb to provide high-precision measurements of the transition frequencies. A photon–ion coincidence detection provided the sensitivity required for the detection of the 20-ms isotope $^{12}$Be. These investigations were motivated twofold, by the nuclear structure aspect and the possibility to provide an important benchmark for bound-state QED calculations in three-electron systems.

Observables of the nuclear ground state that can be measured with high accuracies like masses, charge radii, magnetic dipole and electric quadrupole moments are extremely valuable for nuclear structure physics. The change of the nuclear charge radius along a chain of isotopes is extracted with high precision from optical isotope shifts. This provides insight into differences of the radial distribution of protons and the underlying collective effects of soft or rigid deformation or cluster structures, which are often observed for the few-nucleon systems of light nuclei. Only during the last decade new experimental techniques and precise atomic structure calculations for few-electron systems gave access to the determination of charge radii of low-Z nuclei ($Z < 10$) with unprecedented precision. In 2000, first calculations of the mass shift in three-electron systems [17] provided sufficient accuracy to extract the very small finite nuclear size effect from high-precision isotope shift measurements. Since then, calculational precision for three-electron systems has been improved by two orders of magnitude [18–22]. Pachucki et al. [23, 24] published first results for four-electron systems and recently even showed results that pave the way toward boron-like five-electron systems [25].

Laser spectroscopy experiments on helium and lithium isotopes were strongly motivated by the existence of the so-called halo nuclei. These are nuclear systems with the last neutron(s) being bound by only a few 100 keV, compared to typical nuclear binding energies of the order of 5–7 MeV/nucleon. Due to this weak binding, the neutrons are allowed to tunnel far away from the central core, having a large part of their wavefunctions beyond the classical interaction length of the strong force. These nuclei have been a hot topic in nuclear structure research since their discovery in 1983 [26]. Isotope shifts for such systems were measured previously in helium and lithium isotopes. Single atoms of the short-lived two-neutron and four-neutron halo nuclei $^{6,8}$He were confined in a magneto-optical trap and probed by laser light [27, 28]. The lithium isotopes including the two-neutron halo nucleus $^{11}$Li were investigated by applying two-photon resonance ionization spectroscopy [22, 29, 30]. The beryllium isotope chain contains the one-neutron halo nucleus $^{11}$Be and the isotope $^{12}$Be which in the traditional shell model should have a closed neutron shell. First on-line measurements of transition frequencies and isotope shifts based on laser-cooled $^{7,10}$Be$^+$ ions in a Paul trap were reported in 2006 from the SLOWRI facility at RIKEN, but were limited to accuracies on the order of a few 10 MHz [31]. Further enhancements of this technique were discussed in [32], but improved values of transition frequencies or isotope shifts are not reported so far.

With regard to atomic structure, the vast progress in nonrelativistic few-electron bound-state QED has opened the possibility of additional tests of many-body QED in these light systems. The helium fine structure was recently calculated up to the order $m\alpha ^7$ and is now one of the most precise QED tests in two-electron systems [33]. The application of such calculations to three-electron systems proved to be much harder since the extension of the respective computational methods with explicitly correlated functions turned out to be considerably more difficult. Only recently it became possible to perform a complete calculation of $m \alpha ^6$ and $m \alpha ^7 \ln \alpha$ contributions to the fine structure [34] of a three-electron atom. On the experimental side, measurements of the 2p fine-structure splitting in light three-electron systems are limited in accuracy for isotopes with nonzero nuclear spin due to the unresolved hyperfine structure (hfs) in the $2p\,^2\text{P}_{3/2}$ level. This has been the reason for the fluctuating results on the fine-structure splittings in lithium [22, 35] being reported for a long time. These turned out to be caused by quantum interference effects in the observation of the unresolved resonance lines [36]. Once this issue had been resolved experimentally, good agreement with ab initio calculations was obtained [37]. Since relativistic and QED contributions grow in size with increasing Z, it became important to study the fine-structure splitting also in Be$^+$ to further test bound-state QED.

Both aspects have been addressed with the technique described in this paper. Besides giving a detailed description of the experiment implemented at ISOLDE (CERN), we will present an overview of the spectroscopic results obtained in two beam times (called Run I and Run II). Compared with the techniques used to study helium and lithium isotopes, the collinear approach has the advantage of being more generally applicable and providing high-precision isotope shift data for short-lived isotopes of elements in the so far inaccessible region $4<Z<10$.

Table 1 Theoretical mass shifts $\delta \nu _{\text{MS}}^{9,A}$ and field shift factors $F^{9,A}$ for the D1 and D2 transitions $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2,\,3/2}$ in Be$^+$ with respect to ⁹Be$^+$ obtained in two independent calculations [20, 21, 38, 41] with updated values presented in [2] based on [40, 42]

2 Theory

It is well known that the isotope shift $\delta \nu ^{A,A^{\prime }}$ between two isotopes A and $A^{\prime }$ can be separated into the mass shift $\delta \nu _{\text{MS}}^{A,A^{\prime }}$ and the field shift $\delta \nu _{\text{FS}}^{A,A^{\prime }}$ according to

$$\delta \nu _{\text{IS}}^{A,A^{\prime }}= \nu ^{A^{\prime }}-\nu ^{A}$$

(1)

$$= \underbrace{K_{\text{MS}}\frac{M_{A^{\prime }}-M_{A}}{M_AM_{A^{\prime }}}}_{\delta \nu _{\text{MS}}^{A,A^{\prime }}} + \underbrace{F^{A,A^{\prime }} \delta \left\langle r_{\text{c}}^2\right\rangle ^{A,A^{\prime }}}_{\delta \nu _{\text{FS}}^{A,A^{\prime }}}.$$

(2)

The mass shift contribution (MS) is related to the center-of-mass motion of the atomic nucleus. For light elements this is the major part of the isotope shift, while the small nuclear volume shift $\delta \nu _{\text{FS}}^{A,A^{\prime }}$, being typically at the $10^{-5}$ level of the mass shift, contains the information about the change $\delta \left\langle r_{\text{c}}^2\right\rangle$ in the mean-square nuclear charge radius. Extraction of nuclear charge radii from experimental isotope shifts in the lightest elements requires accurate mass shift calculations. Semi-empirical techniques that have often been applied for heavier elements to evaluate the atomic parameters $K_{\text{MS}}$ and F are not sufficiently accurate. Only state-of-the-art ab initio calculations can provide the accurate mass shift and field shift coefficients. Detailed descriptions of these calculations can be found, e.g.. in [17, 19, 22, 39]. Briefly, the starting point is the nonrelativistic Schrödinger equation which is solved with high numerical accuracy in the basis of Hylleraas coordinates that explicitly take electron–electron correlations into account. The wavefunctions obtained are then used to calculate relativistic and QED corrections perturbatively as a power series in terms of the fine-structure constant $\alpha$. The results for the Be$^+$ isotopes as taken from [20, 21, 40, 41] are listed in Table 1. It is worthwhile to note that the calculations performed by two independent groups agree within uncertainties for all isotopes. The only significant difference concerns the case of $^{11}$Be, where the nuclear polarizability correction of 211 kHz has been calculated and included in [41] but not in [40]. The field shift factor $F^{9,A}$ has been calculated for each isotope individually and is almost constant along the isotopic chain, besides a small difference in the relativistic correction. Using the mass shift values from the table and the measured isotope shifts, the change in the mean-square nuclear charge radius can be determined using

$$\delta \langle r_{\text{c}}^2 \rangle ^{9,A} = \frac{\delta \nu _{\text{IS}}^{9,A}-\delta \nu _{\text{MS}}^{9,A}}{F^{9,A}}.$$

(3)

The total charge radius $R_{\text{c}}(A) = \sqrt{\langle r_{\text{c}}^2 \rangle ^A}$ of at least one (or more) stable isotope(s) determined by other methods is required to obtain total charge radii of the radioactive isotopes. In the case of beryllium the nuclear charge radius of the stable ⁹Be nucleus was determined from elastic electron scattering [43] and thus

$$R_{\text{c}}(^{A}{\text{Be}}) = \sqrt{R_{\text{c}}^2(^9{\text{Be}}) + \delta \langle r_{\text{c}}^2 \rangle ^{9,A}}.$$

(4)

Fig. 1

Experimental setup for the beryllium measurements at ISOLDE. Two dye laser systems were used to excite the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2,\, 3/2}$ transitions in Be$^+$. The dye laser for collinear excitation (left) was operated at a fundamental wavelength of 624 nm and stabilized to a hyperfine transition of molecular iodine. The output beam is frequency doubled to 312 nm and guided into the beam line. The other laser (right) is locked to a frequency comb. After frequency-doubling to 314 nm the UV laser beam is anticollinearly superposed with the ion beam. The resonance fluorescence is detected by a pair of photomultipliers. A photon–ion coincidence detection unit increases the detection efficiency if the ion beam rate is low (not shown, see Fig. 3)

The many-electron Dirac equation poses some difficulties for the inclusion of relativistic effects and correlations between electrons in atomic systems. According to QED the equation has to include multiple electron–positron pairs, which leads to numerical instabilities. This problem limited the relativistic calculation of the lithium $2p\,^2{\text{P}}_{1/2}$ – $2p\,^2{\text{P}}_{3/2}$ splitting to one significant digit [44]. Forty years after first numerical calculations using explicitly correlated basis sets with Hylleraas and Gaussian functions for two electrons [45], Puchalski and Pachucki extended such calculations to three-electron systems [34]. Nonrelativistic QED can perturbatively account for relativistic, retardation, electron self-interaction, and vacuum polarization contributions by an expansion of the level energy in powers of the fine-structure constant $\alpha$

$$E = m\alpha ^2 E^{(2)} + m\alpha ^4 E^{(4)} + m\alpha ^5 E^{(5)} + m\alpha ^6 E^{(6)} +\cdots ,$$

(5)

where the expansion coefficients $E^{(i)}$ may include powers of $\ln \alpha$. In this expansion, the fine structure arises at the order of $m\alpha ^4$, together with the nuclear recoil term, which in this order is comparable in size to $m\alpha ^6$ contributions, but of opposite sign. For all details of the calculations and the individual contributions we refer to [46]. In the splitting isotope shift (SIS), i.e., the difference in fine-structure splitting between isotopes, all mass-independent terms cancel and only the mass-dependent terms remain, which can be calculated with very high accuracy.

The SIS therefore provides a valuable consistency check of the experimental results [47]. For isotopes with nuclear spin, hyperfine-induced fine-structure mixing can lead to an additional level shift that also contributes to the SIS. This in combination with the unresolved hyperfine splittings in the $2p\,^2{\text{P}}_{3/2}$ level in light three-electron systems makes even–even isotopes with nuclear spin $I=0$ an exceptionally suitable case to perform tests of the calculations. While there is no such isotope for lithium, the beryllium chain with $^{10}$Be and $^{12}$Be includes two spinless isotopes that are accessible to the measurement.

3 Experimental setup

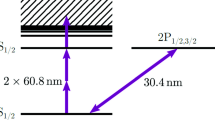
A schematic overview of the experimental setup applied for collinear laser spectroscopy on Be$^+$ ions in the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ (D1) and $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{3/2}$ (D2) transitions is shown in Fig. 1. A mass-separated ion beam of a stable or a radioactive beryllium isotope at an energy up to 60 keV was transported to the laser beam line. Two frequency-stabilized dye laser systems delivered UV beams that superposed the beryllium ion beam in opposite directions. The resonance fluorescence photons were detected via photomultipliers. The resonance condition was established by tuning the Doppler-shifted frequency with an electrical potential applied to the fluorescence detection chamber. The individual parts of the experimental setup as well as the scanning procedure are described in detail in the following subsections.

3.1 Production of radioactive beryllium isotopes

The stable and radioactive beryllium isotopes were produced at the on-line isotope separator facility ISOLDE at CERN. High-energy (1.4 GeV) protons from the PS Booster synchrotron impinge on a uranium carbide target. The atoms are photo-ionized using the resonance ionization laser-ion source RILIS [49]. Resonant excitation at 234.9 nm from the atomic ground state in the $2s^2$ $^{1}{\text{S}}_0 \rightarrow 2s 2p\,^1\text{P}_{1}$ transition, followed by excitation at 297.3 nm to the auto-ionizing $2p^2$ $^{1}{\text{S}}_0$ level was employed to ionize the Be atoms which have the rather large ionization potential of 9.4 eV.

Table 2 lists the ion beam intensities decreasing from $^{7}\text{Be}$ to $^{12}$Be by seven orders of magnitude [48]. In the final stage of our experiment an upgraded solid-state pump laser system [49] was used. This gave a $^{11}$Be yield of up to $2.7 \cdot 10^7$ ions/s, about 4 times larger than reported previously.

The yields are sufficient to perform collinear laser spectroscopy on $^{7-11}$Be solely based on a standard fluorescence detection system. However, for a beam intensity of ${<}10^4$ ions/s, i.e., for measurements on $^{12}$Be, the sensitivity had to be enhanced. This was achieved by detecting ion–photon coincidences and thus rejecting the stray light background which usually determines the sensitivity limit. Coincidence detection requires an isobarically clean ion beam. For that reason the pulse structure and possible contamination of the beam was investigated and optimized for $^{12}$Be.

Table 2 Nuclear properties and production rates of the beryllium isotopes at the ISOLDE facility at CERN

3.2 Beryllium ion beam structure

During our experiment at ISOLDE, pulses of $3 \cdot 10^{13}$ protons impinged on a UC$_x$ target typically every 4 s. The release of resonantly ionized $^{12}$Be was tracked using a secondary electron multiplier installed at the end of the laser spectroscopy beam line. The proton pulses triggered a multichannel analyzer that recorded the ion events as a function of time. Figure 2 shows such a release curve summed over 100 proton pulses with a resolution of 0.2 ms/channel. The integral corresponds to a release of 12 000 ions per proton pulse. This is almost a factor of 10 more than listed in the yield table (Table 2). During the measurements on $^{12}$Be the typical ion yield was about 8000 ions/pulse.

The release curve of Fig. 2 demonstrates a characteristic feature of the ISOLDE HV supply: First ions are detected about 2–3 ms after the proton pulse hit the target. This delay is determined by the recovery time of the high voltage, which is pulsed down right before a proton pulse hits the target, in order to reduce the current load from ionized air [51]. After an initial steep rise the release curve follows essentially the exponential decay of $^{12}$Be. The extracted half-life of $T_{1/2} \approx 21.9 (8)$ ms agrees well with the literature value of 21.50 (4) ms [50]. The single exponential does not exhibit any significant offset. This demonstrates that practically no beam contamination from the isobar $^{12}$C$^+$ is present and $^{12}$B$^+$ (having a similar lifetime as $^{12}$Be) is also not expected due to the relatively high ionization potential. This situation is prerequisite for the application of a photon–ion coincidence technique, which otherwise would suffer from random coincidences between scattered laser light and isobaric ions. With the rapid decay of $^{12}$Be the fluorescence detection can be limited to about 100 ms after the proton pulses.

Fig. 2

Release of beryllium ions (solid blue line) from ISOLDE as a function of time after the proton pulse hit the target container, measured with a secondary electron multiplier at the end of the COLLAPS beam line. The release curve, integrated over 100 proton pulses with a resolution of 0.2 ms/channel, is modeled with an exponential decay curve (dash-dotted red line)

3.3 Experimental beam line

The COLLAPS collinear spectroscopy beam line at the ISOLDE facility was commissioned in the early eighties [52–54] and has been improved continuously [8, 15, 55–58] with the objective of widening the range of accessible elements and isotopes. An important aspect was the development of highly sensitive alternatives to the traditional fluorescence photon detection technique. For conventional collinear spectroscopy the ions are accelerated to a beam energy of typically 50 keV, with the corresponding positive potential applied to the ion source, while the mass separator and the experimental beam line are on ground potential. The ion beam is merged with a laser beam by a pair of deflector plates as shown in Figs. 1 and 3.

Fig. 3

Schematic view of the COLLAPS beam line at ISOLDE/CERN and corresponding high-voltage circuits: A mass-separated ion beam is directed along the axis of the vacuum beam line with the help of an electrostatic deflector. An electric dipole and quadrupole collimate and steer the beam through the apparatus. The fluorescence detection region is a cage floated on a variable potential against ground to enable Doppler-tuning. At the end of the beam line a photon–ion coincidence detection chamber is installed, whereby a secondary electron multiplier is used to count the ions. The generation and measurement of the high-voltage potential is explained in the text

A quadrupole triplet collimates the ion beam, matching it to the laser beam profile, and a second set of deflector plates aligns it with the laser beam axis which is defined by two apertures at a distance of about 2 m. Two UV-sensitive photomultiplier tubes with 45 mm active aperture and 15% quantum efficiency at 313 nm are used for fluorescence detection. The light collection system consists of two fused-silica lenses of 75 mm diameter and a cylindrical mirror opposite to them. Stray laser light is suppressed by sets of apertures with diameters decreasing with distance from the optical detection region and Brewster-angle quartz windows at both ends.

Collinear laser spectroscopy is usually performed with the laser running at a fixed frequency, while the absorption frequency of the ions is tuned by changing their velocity (Doppler-tuning). This means that a variable electrical potential has to be applied to the interaction region. For applying post-acceleration/deceleration voltages up to 10 kV a set of four electrodes provides a smoothly variable potential along the beam axis. In order to avoid optical pumping into dark states, the final ion velocity is reached just in front of the detection region by applying a small fixed offset voltage between the last electrode and the detection chamber. The lower part of Fig. 3 illustrates the generation of the voltage between the detection region and ground as a combination of a static high voltage in the range of ${\pm }10$ kV and a scanning voltage of ${\pm }500$ V. The latter is created by amplification (${\times }50$) of the ±10 V dc output of an 18-bit DAC controlled by the measuring computer. This voltage defines the floating offset potential of a stabilized ${\pm }10$ kV power supply. The combination of power supplies makes it possible to perform measurements on a series of isotopes with different Doppler-shifts and for each of them scan small frequency ranges covering the hyperfine structure with high resolution.

Both the static high voltage and the scanning voltage are measured with a high-precision 1:1000 voltage divider and a digital voltmeter. A comparison of the measured voltages with those obtained using a precision voltage divider calibrated at PTB (Braunschweig, Germany) [59] has demonstrated an uncertainty of $\Delta U/U < 3 \cdot 10^{-5}$ which corresponds to about 0.3 V at a maximum voltage of 10 kV applied to the excitation region [60]. Still, the knowledge of the ion beam velocity is limited by the uncertainty of the ion source potential which is determined by the main acceleration voltage power supply. Also, the specified accuracy $\Delta U/U < 1 \cdot 10^{-4}$ of the voltage measurement on the operational voltage of 60 kV was verified by calibration with the precision voltage divider. It translates to <6 eV uncertainty in the ion beam energy.

As in the laboratory frame the transition frequency of the ions in collinear geometry scales as

$$\nu _{c} = \nu _0 \, \gamma \, \left( 1 + \beta \right)$$

(6)

where the dimensionless ion velocity is $\beta = v/c$, the relativistic factor $\gamma = \sqrt{1/(1-\beta ^2)}$ and the transition frequency $\nu _0$. Any uncertainty in $\beta$ arising from the ion source potential results in an uncertainty of measured transition frequencies or isotope shifts, especially for light ions. In the particular case of beryllium a deviation of 6 V from the measured voltage result in an artificial isotope shift of $\delta \nu ^{9,11} \left( ^{9} \text {Be},^{11}\text {Be} \right) = 18$ MHz. To overcome these limitations, we have introduced the (quasi-)simultaneous excitation by a collinear and an anticollinear laser beam. The method is based on the fact that in this geometry the measured resonance frequencies, $\nu _{c} = \nu _0 \gamma (1+\beta )$ for collinear and $\nu _a = \nu _0 \gamma (1-\beta )$ for anticollinear excitation are simply related to the rest-frame frequency $\nu _0$ by

$$\nu _{c} \cdot \nu _{a} = \nu ^2_0 \gamma ^2 \cdot \left( 1 + \beta \right) \left( 1 - \beta \right) = \nu ^2_0.$$

(7)

This provides a method to determine the transition frequency independently of the knowledge of the ion beam energy which depends on assumptions about the ion source potential and on measured voltages. However, in contrast to conventional collinear laser spectroscopy, this approach requires two laser systems instead of one and, additionally, the capability to determine the laser frequencies with an accuracy better than $10^{-9}$. Similar approaches were proposed and demonstrated for the measurement of transition frequencies [61] and used for, e.g., precision spectroscopy in the fine structure of helium-like Li$^+$, yielding an accurate value of the Lamb shift [62]. Here we have developed a procedure which is widely applicable in cases where high precision is required for the spectroscopy of unstable isotopes.

3.4 Setup and specification of the frequency-comb-referenced laser system

The transition wavelength of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2,\, 3/2}$ transitions in Be$^+$ is about 313 nm corresponding to an energy splitting of $\approx 4$ eV. The laser system installed at COLLAPS is schematically shown in Fig. 1. For anticollinear excitation a frequency doubled Nd : YVO$_4$ laser (Verdi V18) was operated at 9 W to pump a Coherent 699-21 dye laser. Using a dye solution of Sulforhodamine B in ethylene glycol, a typical output power of 700 mW was achieved at the wavelength of 628 nm. Another dye laser, Sirah MATISSE DS, was installed for collinear excitation and operated with a dye solution of DCM in 2-phenoxy-ethanol. With the 8-W pump beam from a Verdi V8, about 1.2 W were achieved at the fundamental wavelength of 624 nm. Each laser beam was then coupled into a 25-m long photonic crystal fiber (LMA-20) to transport the laser light to one of the second harmonic generators installed in the ISOLDE hall. A two-mirror delta cavity (Spectra Physics Wavetrain) and a four-mirror bow-tie cavity (Tekhnoscan FD-SF-07) were located nearby the COLLAPS beam line. A Brewster-cut and an antireflection coated BBO crystal, respectively, converted the laser beams of 628 and 624 nm into their second harmonics at 314 and 312 nm, in both cases with an output of more than 10 mW. The elliptical UV beams were reshaped to circular beams with diameters of 3–4 mm to match the transversal profile of the ion beam and finally attenuated to powers below 5 mW. Two remote-controlled fast beam shutters blocked alternatively the collinear or the anticollinear laser beam. This enabled us to perform scans of 3–30 s duration in collinear or anticollinear configuration in a fast sequence.

Fig. 4

Beat frequency histograms of the frequency-stabilized dye lasers. The beat was averaged for 1 s, and the distribution of the beat frequencies over a period of 2 h is shown in the histogram. Graph (a) shows the histogram of the MATISSE DS laser stabilized to a hyperfine transition of molecular iodine. The corresponding uncertainty was estimated as the FWHM of a Gaussian fit (red) of about 75 kHz. The results of the frequency-comb stabilized Coherent 699-21 dye laser are depicted in Graph (b). In this case the FWHM is approximately 400 Hz

The backbone of the laser system was the precise frequency stabilization and frequency measurement required for the application of Eq. (7). In practice, the transition rest-frame frequency $\nu _0$ depends on the frequencies of both dye lasers in the laboratory frame which have to be known with a relative accuracy better than $\Delta \nu /\nu \le 10^{-9}$ to yield the isotope shifts with an accuracy better than $10^{-5}$. Therefore, a Menlo Systems frequency comb (FC 1500) with a repetition frequency of 100 MHz was employed. A Stanford Research rubidium clock (PRS10) provided the 10-MHz reference for the stabilization of the carrier-envelope-offset (CEO) and the repetition frequency. This clock was long-term stabilized using a GPS receiver tracking the 1-pps signal.

The MATISSE dye laser for collinear excitation was stabilized to its internal reference cavity for short-term stability. In this case frequency drifts were further reduced by locking the laser to a hyperfine transition in molecular iodine using frequency-modulated saturation spectroscopy. In total 12 hyperfine transitions of $^{127}$I$_2$ match the desired Doppler-shifted frequencies for a wide range of acceleration voltages between 30 and 60 kV. The demodulated dispersion signal from the phase-sensitive detection was fed into a 16-bit National Instruments DAQ card (NI-DAQ 6221) and further processed with the MATISSE control software to provide a counter-drift for the MATISSE reference cavity. In regular time intervals the laser frequency was measured with the frequency comb and recorded for a few 100 s to ensure the stability of the locking point and to provide the laboratory-frame frequency for the application of Eq. (7). A histogram of 1-s averaged beat signals measured over 2 h is depicted in Fig. 4a. It exhibits a Gaussian distribution with standard deviation of about 75 kHz. The frequency of the Matisse laser stabilized to the various iodine lines was repeatedly measured during the beam times. The averaged results are listed in Table 3 and compared with the calculated frequencies from [63]. Reasonable agreement is obtained in all cases.

Table 3 Frequencies of the $a_1$ hyperfine component in various transitions of iodine $^{127}$I$_2$ utilized and determined during the experiment

The Coherent 699 dye laser for anticollinear excitation was internally stabilized to its own reference cavity of Fabry-Perot type; long-term frequency drifts were corrected by an additional stabilization to the frequency comb. Therefore, the beat signal between the dye laser and the nearest frequency comb mode was detected on a fast photo diode and fed into the Menlo Systems phase comparator DXD 100. A low-noise PI regulator (PIC 210) processed the signal from the phase comparator and provided a servo-voltage to counteract all frequency excursions of the dye laser by correcting the length of the reference cavity. As a measure of the long-term stability a beat signal with the frequency comb was detected. The result is shown in Fig. 4b. The standard deviation over 2 h measuring time and 1-s averaging time is about 400 Hz.

4 Measurement procedure

The ion beam acceleration voltage at the ISOLDE front end was fixed to 40 kV. A suitable iodine line is chosen such that the isotope under investigation can be recorded by applying an offset voltage in the available range of $U_{\text{{Offset}}}=\pm 10$ kV at the fluorescence detection region. For example, when choosing the $a_1$ hyperfine component in the transition R(56)(8-3) as a reference, the isotopes $^{9-12}$Be can be addressed. The scan voltage range $U_{\text{scan}}$ of up to ${\pm }500$ V is then adjusted to cover the full hyperfine structure in the collinear direction, and the expected position of the center of gravity is calculated. The required offset voltage as well as the scan voltage range was estimated based on previous measurements of the ⁹Be transition frequency [66] and nuclear moments [15] in combination with the precisely calculated mass shift [40, 41]. Once the resonance position of ⁹Be was found, the laser frequencies $\nu _c$ and $\nu _a$ could be predicted for all radioactive beryllium isotopes with an accuracy of a few MHz, which is the size of the expected field shift contribution. This knowledge allowed us to calculate the required frequency of the second dye laser to simultaneously cover the full hyperfine structure in anticollinear geometry within the same Doppler-tuning voltage range and even to ensure that the centers of gravity of both hyperfine spectra practically coincide within a few 100 mV, corresponding to the size of the field shift contribution. This is only possible because this dye laser is locked to the frequency comb and thus can be stabilized at any arbitrarily chosen frequency.

Fast laser beam shutters placed in front of the Brewster windows of the apparatus were controlled by the data acquisition software in order to allow only one of the two laser beams to enter. For the isotopes with half-lives longer than the typical 4-s repetition time of proton pulses, fast scans of the Doppler-tuning voltage $U_{\text{{scan}}}$ were performed with alternating laser beams. The scanning range was chosen depending on the hyperfine splitting of the respective isotope, and spectra were taken in 200 channels for $^{10}$Be and up to 800 channels for the odd-A isotopes $^{7,9,11}$Be. The common dwell time was 22 ms per voltage step. Depending on the ion beam intensity, a single spectrum is the sum of 50–800 individual scans for each direction. This procedure was applied using about 3–4 different iodine lines for each isotope.

Because of the short 21.5-ms half-life of $^{12}$Be, photon counts had to be accumulated for typically 60 ms after each proton pulse. The laser shutters for collinear and anticollinear beams were switched between consecutive pulses, and the voltage steps were triggered by every second pulse. Given the extremely low ion beam intensity, the single-line spectrum of $^{12}$Be was taken in only 20 channels with a total measuring time of about 8 hours, corresponding to 200 scans.

Fig. 5

Comparison between conventional optical fluorescence detection (upper trace, right y axis) and photon–ion coincidence detection (lower trace, left y axis) at an ion beam rate of 30,000 $^{10}$Be$^+$ ions/s. The optical spectrum (black circles) in the conventional detection is covered by stray light of the laser beam. In the photon–ion coincidence spectrum a clear resonance (blue circles) is observed, fitted with a Voigt profile

Detection of the weak $^{12}$Be signals required the additional rejection of background from scattered laser light reaching the photomultiplier tubes. This was achieved by implementing a photon–ion coincidence: Photomultiplier signals were accepted only if an ion was simultaneously traversing the detection unit. Downstream of the photon detection chamber the ions were deflected onto the cathode of a secondary electron multiplier (SEM) installed off-axis. Discriminated pulses from the photomultipliers were delayed by the appropriate time of flight (TOF) (3–4 $\mu$s) of the ion to the SEM. To avoid electronic dead times, the delay was realized logically in a first-in first-out (FIFO) queue structure on a field-programmable gate array (FPGA) with a resolution of 10 ns, based on the FPGA’s internal clock. Signals leaving the queue were transformed back into a TTL pulse and fed together with the SEM pulses into a standard coincidence unit. The photon–ion coincidence detection was optimized using a $^{10}$Be$^+$ ion beam, attenuated to about 30,000 ions/s by detuning the RILIS laser. The time of flight for ⁹Be was determined with a multichannel analyzer, and the respective TOF for $^{10}$Be was calculated. Figure 5 shows a comparison between the conventional ungated spectrum (gray circles) and the optical spectrum detected in delayed coincidence (blue circles). The resonance peak is only visible in the gated spectrum. The background induced by laser stray light was reduced by a factor of 35. However, it must be noted that this reduction factor strongly increases with a reduction of the ion beam rate.

5 Analysis and results

Two beam times were performed to investigate first the isotopes $^{7-11}$Be (Run I) [1] and then concentrate on $^{12}$Be (Run II) [2] after installing the ion–photon coincidence setup. The stable isotope ⁹Be and the even–even isotope $^{10}$Be were used as reference isotopes, respectively. We concentrate here on results and procedures from Run II and provide differences to Run I only when it is of importance.

5.1 Line shape studies on ⁹Be and ¹⁰Be

Resonance spectra of ⁹Be in the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition are shown in the upper trace of Fig. 6 taken in collinear (left) and anticollinear geometry (right) as a function of the Doppler-tuned laser frequency. Each spectrum is the sum of 20 individual scans. To avoid saturation broadening, the laser beam was attenuated to 3 mW and collimated to a beam diameter of about 3–4 mm to match approximately the size of the ion beam. Similar spectra for $^{10}$Be are shown in the lower traces. These are the integral of 50 single scans at an ion beam current of 10 pA. A best fit of the resonance was obtained for a double Voigt profile with a full width half maximum (FWHM) of 40 MHz. It becomes apparent that each peak in the hyperfine structure is actually a composition of two components: A satellite peak, with a typical intensity of <5% of the corresponding main peak, appears on the low-energy tail in each spectrum independent of the direction of excitation. It is induced by a class of ions which have lost some of their kinetic energy. The loss is almost exactly 4 eV and can be explained by inelastic collisions with residual gas atoms that lead to excitations into the 2p states. The energy required for this excitation is taken from the kinetic energy of the ion and is lost when the excited ion decays to the ground state by emitting a photon. The overall line shape is reasonably well fitted using a Voigt doublet and only small structures remain in the residua, depicted below each spectrum. The remaining small asymmetry seen in this structure is similar for the different peaks. It is an asset of the technique that asymmetries in the collinear and the anticollinear spectra shift the peak center to slightly lower and slightly larger frequencies, respectively. Hence, these shifts largely cancel when calculating the rest-frame frequency.

5.2 Hyperfine fitting procedure

Fitting was performed as follows: Each voltage information was converted into the corresponding Doppler-shifted laser frequency to account for the small nonlinearities in the voltage–frequency relation. Hyperfine peak positions relative to the center of gravity $\nu _{\text{cg}}$ were calculated based on the Casimir formula.

Fig. 6

Top optical hyperfine spectrum of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition in $^{9}$Be$^+$ for collinear (left) and anticollinear excitation (right). Spectra were taken at 35-kV ISOLDE voltage and are the sum of 20 individual scans with a resolution of 400 channels. Hyperfine spectra are fitted using a multiple Voigt profile for each component (red line, for further details see text). Striking is the appearance of a small satellite peak on the left of each component which is ascribed to energy loss of the ions in inelastic collisions in flight. The differential Doppler-tuning parameter is about 39 MHz/V. Bottom resonance spectra of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition in $^{10}$Be$^+$ again in collinear and anticollinear geometry also fitted with a Voigt doublet. A small structure in the residua (shown on the bottom of each graph) remains in all cases, which is discussed in the text

The position of each hfs sublevel with total angular momentum $\mathbf {F}=\mathbf {I}+\mathbf {J}$, composed of electronic angular momentum J and nuclear spin I, and $C=F(F+1)-I(I+1)-J(J+1)$ is given to first order by the hyperfine energy

$$\Delta E_{\text{hfs}}=\frac{A}{2}C+B\cdot \frac{\frac{3}{4}C(C+1)-I(I+1)J(J+1)}{2I(2I-1)J(2J-1)} \ .$$

(8)

In the fit function, these shifts determine the spectral line positions relative to the center of gravity. The factors A and B (only for $2p\,^2{\text{P}}_{ 3/2}$) of the upper and the lower fine-structure state of the transition and the center of gravity $\nu _{\text{cg}}$ are the free-fitting parameters for the peak positions. The line shape of each component was modeled by two Voigt resonance terms representing the main peak and the satellite peak as discussed above. The distance between the two peaks was fixed to 4 V on the voltage axis. The Gaussian (Doppler) line width parameter and the intensity ratio between the main peak and the satellite were free parameters but constrained to be identical for all hyperfine components, while the total intensity of each component was also a free parameter. The Lorentzian line width was kept fixed at the natural line width of 19.64 MHz since significant saturation broadening was not observed. Nonlinear least-square minimization of $\chi ^2$ was performed using a Levenberg–Marquardt algorithm.

Fitting the collinear and the anticollinear spectra independently, we obtain in both cases the centroid frequency $\nu _{\text{cg}}$ of the hyperfine structure. However, for calculating the transition rest-frame frequency $\nu _0$ we must take into account that Eq. (7) requires $\nu _c$ and $\nu _a$ to be measured at the same ion velocity. This is only the case if the center of gravity appears in both spectra at the same voltage. This was accomplished approximately by changing the frequency of the laser used for anticollinear excitation until the deviation between the corresponding centers of gravity was typically smaller than 3 V, facilitated by the fact that the comb-stabilized laser can be locked at any arbitrary frequency. The remaining small shift $\delta U$ was considered in the analysis by correcting the collinear frequency using the linear approximation $\delta \nu = \frac {\partial \nu }{\partial U} \cdot \delta U$, where U is the total acceleration voltage of the ions which have entered the optical detection region. Hence, the transition rest-frame frequency was calculated according to

$$\nu _0 = \sqrt{\left( \nu _c - \frac{\partial \nu _{\text{D}}}{\partial U} \cdot \delta U \right) \cdot \nu _{a}} - \delta \nu _{\text{rec}}.$$

(9)

with the differential Doppler-shift

$$\frac{\partial \nu _{\text{D}}}{\partial U} = \frac{\nu _0}{mc^2}\left( e+\frac{e(mc^2+eU)}{\sqrt{eU(2mc^2+eU)}} \right)$$

(10)

and the recoil correction term

$$\delta \nu _{\text{rec}} = \frac{h \nu ^2_{\text{photon}}}{m_0c^2}.$$

(11)

The latter takes energy and momentum conservation during the absorption/emission process into account. It contributes with about 200 kHz to the transition frequency and is slightly isotope dependent. Each measurement of $\nu _0$ was repeated at least five times for each isotope. Statistical fitting uncertainty of the center of gravity was usually <100 kHz. For each pair of collinear/anticollinear spectra the rest-frame transition frequency was calculated, and the final statistical uncertainty was then derived as the standard error of the mean of all measurements being usually of the order of 100–500 kHz.

5.3 Investigations of systematic uncertainties

Sources of systematic errors were investigated on-line in Run I and Run II as well as in an additional test run, when only a previously irradiated target was used to extract the long-lived isotope $^{10}$Be. For each isotope about 3–4 different iodine hyperfine transitions were used as reference points for the collinear laser frequency, which implies different locking frequencies of the comb-locked anticollinear laser as well as different offset voltages at the fluorescence detection region. It should be noted that the actual locking frequency of the iodine-locked laser was regularly checked with the frequency comb during each block of measurements.

In Run I, the Rb reference clock for the frequency comb was not long-term stabilized on the 1-pps signal and contributed with about 350 kHz to the systematic uncertainty of the transition frequency [1].

Additional uncertainties related to the applied acceleration voltages could only arise from the center-of-gravity correction according to Eq. (9), which was typically <3 V. The HV-amplification factor, calibrated regularly to better than $3 \cdot 10^{-4}$, leads to uncertainties clearly below the 3-mV level corresponding to approximately 100 kHz in transition frequency. This contribution can be safely neglected compared to other systematic uncertainties discussed below.

Additionally, ion and laser beam properties were modified on purpose for investigating a possible influence on the measured transition frequencies and isotope shifts. In deviation from a parallel collimation the ion beam was focused close to the fluorescence detection region with the available electrostatic quadrupole lenses. Similarly, additional convex lenses were added into the light path to focus the laser beams inside the beam line. It was found that these modifications merely changed the signal-to-noise ratio but had no significant influence on the determined resonance frequencies.

5.3.1 Laser-ion-beam alignment

The parallel and antiparallel alignment of the respective laser beams with the ion beam was ensured using two apertures inside the beam line. Hence, the range of a possible angle misalignment between laser and ion beam was estimated taking the full aperture of 5 mm and their distance to each other of 2 m into account. A conservative estimate with beam diameters of about 4 mm results in an angle of $\alpha = \arctan \left( \Delta z / \Delta x\right) \approx 1$ mrad. However, during the preparation of the experiment, both laser beams were superimposed 2 m after the collinear and anticollinear exit windows, respectively. Two extreme cases are to be discussed: The Doppler-shifted frequencies $\nu _{c,a}$ get angle dependent if both laser beams are well superposed, but are misaligned relative to the ion beam

$$\nu _{c,a} = \nu _0 \gamma ( 1 \pm \beta \cdot \cos \alpha ).$$

(12)

Then the transition rest-frame frequency $\nu _{0}$ becomes angle dependent as well

$$\nu _{0}= \frac{1}{\gamma } \sqrt{\frac{\nu _c \cdot \nu _{ac}}{1 - \beta ^2 \cdot \cos ^2\alpha }}$$

(13)

$$= \sqrt{\frac{1 - \beta ^2}{1 - \beta ^2 \cos ^2 \alpha }} \sqrt{\nu _c \cdot \nu _{ac}}.$$

(14)

Even though the Doppler-shift is reduced for both beams, the collinear–anticollinear geometry almost leads to a cancellation of the effect; the anticollinear resonance is less blue shifted while the collinear resonance is less red shifted. For an angle misalignment of 1 mrad, $\nu _a$ and $\nu _c$ will each be shifted by as much as 1.4 MHz, whereas the effect on $\nu _0$ is only of the order of about 1 kHz.

The other extreme is a misalignment of one laser relative to a well superposed laser-ion–beam pair. Then the transition frequency $\nu _0$ becomes

$$\nu _{0}= \frac{1}{\gamma } \sqrt{\frac{\nu _c \cdot \nu _{ac}}{(1 - \beta \cdot \cos \alpha ) ( 1+\beta )}}$$

(15)

$$= \sqrt{\frac{ 1 - \beta }{(1 - \beta \cos \alpha })}\sqrt{\nu _c \cdot \nu _{ac}}$$

(16)

$$\approx \left( 1 - \beta \alpha ^2 \right) \sqrt{\nu _c \cdot \nu _{ac}}.$$

(17)

In contrast to Eq. (13) this angle-dependence can lead under unfavorable conditions to an appreciable shift. The influence of the laser-ion-beam alignment was extensively studied using a stable ⁹Be ion beam by misaligning one of the laser beams so that a deviation was clearly visible in the horizontal or vertical direction. With the typical beam diameter a deviation of about 2 mm across a distance of $\approx 8$ m ($\alpha =0.25$ mrad) was detectable, corresponding to a total effect of about 600 kHz. Misalignment and realignments were repeated several times but the results of the measurements with misalignment scattered similarly as the measurements with optimized alignment, and in both cases the scatter was in accordance with the standard deviation of all regular ⁹Be measurements. During the experiment, the counterpropagating alignment of the laser beams was inspected visually several times per day. A systematic uncertainty of 300 kHz, corresponding to half the full scattering amplitude was conservatively estimated.

Fig. 7

Power dependence of the extracted frequency of $^{10}$Be$^+$ in the D1 (left) and the D2 transition (right). Plotted are the differences to the total mean frequency as a function of laser power. Copropagating and counterpropagating laser beams were adjusted to approximately equal power. Measurements were performed in three series varying the power from the highest to the lowest values. Uncertainties of the individual data points were estimated as the standard deviation for each individual set of three measurements at approximately the same power from this series

5.3.2 Photon recoil shift

Repeated interaction with a laser beam can influence the external degrees of motion of an ion or atom as it is well known from laser cooling and laser deceleration in a Zeeman slower. In collinear laser spectroscopy the repeated directed absorption and isotropic reemission of photons will have the consequence that the ions are either accelerated (collinear excitation) or decelerated (anticollinear excitation). With every absorbed photon, the Doppler-shifted resonance frequency is shifted toward higher frequencies ($\nu _{c}$ and $\nu _{a}$) for both directions and this systematic shift results in a transition frequency $\nu _0$ that is too large. The combination of light ions and ultraviolet photons leads to an exceptionally large photon recoil, and the possible influence of this effect must be studied. Due to the absence of hyperfine splitting the $2s \rightarrow 2p$ transitions in the even isotopes $^{10,12}$Be$^+$ are closed two-level systems. Hence, the possibility of repeated photon scattering is enhanced compared to the odd-mass isotopes which are pumped into a dark hyperfine state after a few absorption–emission cycles. To investigate whether the photon recoil has a measurable effect, the power dependence of the transition frequency of $^{10}$Be was determined as a function of the laser power. The laser power in both beams was increased stepwise and simultaneously from below 1 mW up to 6 mW. The deviation of the extracted transition frequencies from the mean frequency determined for the D1- and D2-transition is plotted in Fig. 7 as a function of laser power. Each data point is associated with an uncertainty estimated as the standard deviation of a block of three measurements at similar power. In both transitions the peak positions scatter but do not show a common trend upwards or downwards. It appears, however, that we observe at photomultiplier tube 2 (PMT2), located about 15 cm downstream from PMT1, resonances that are systematically higher in frequency than at PMT1.

As a consequence of this observation we have included only data from PMT1 in the analysis and have estimated an additional uncertainty for the remaining effect. The average difference between PMT1 and PMT2 is about 300 and 450 kHz in the D1 and D2 transition, respectively. Since the distance between the two PMTs is slightly larger than the path of the ions before reaching PMT1, we estimate conservatively a maximal shift of about 400 kHz for the systematic uncertainty $\Delta \nu _{\text{{Ph}}}$ caused by photon recoil.

5.4 Spectra of the short-lived isotopes $^{7,11,12}$Be

A typical spectrum of $^{7}$Be is depicted in Fig. 8. It is the sum of 50 individual scans, taken in the first beam time in 2008. Here, line shapes are slightly broader than observed in the second beam time [65]. Since the measurements on $^{7}$Be were not repeated in 2010, the uncertainties of the fitted line positions are larger than for the other isotopes. The reduced line width in the second beam time is clearly visible in the spectrum of $^{11}$Be depicted in Fig. 9. This is the sum of 400 individual scans. Spectra of the unresolved hyperfine structure in the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{3/2}$ transitions of both these isotopes can be found in [65].

Fig. 8

Spectra obtained in the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition in $^{7}$Be$^+$ for copropagating (left) and counterpropagating laser excitation (right) as a sum of 50 individual scans. The data points are fitted with a multiple Voigt profile as discussed in the text. In the lower trace the residua of the fit are displayed. For more details see [65]

Fig. 9

Resonance spectra of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition in $^{11}$Be$^+$ in collinear (left) and anticollinear direction (right). The production rate was about $10^6$ ions / pulse, and thus 400 individual scans were accumulated. The data points are fitted with a multiple Voigt profile as discussed in the text. Fitting residua are displayed in the lower trace

For the investigation of $^{12}$Be$^+$, proton pulses impinged on the target every 3–5 s. In this case, spectra in co- and counterpropagating geometry were taken by switching the laser beams after each proton pulse and photon detection was limited to 60 ms ($\approx 3\,T_{1/2}(^{12}{\text{Be}})$) after the pulse to reduce the number of random coincidence events. Figure 10 shows a typical spectrum which is accumulated over 180 individual scans. Here a detection efficiency of about 1 photon per 800 ions was obtained. The Doppler-tuning voltage range was restricted to 6 V corresponding to about 200 MHz frequency span around the main peak, to limit the time required to record a single resonance to a few hours. Reference measurements of $^{10}$Be$^+$ were interspersed after every 40 single scans to ensure stability of all conditions. Due to the limited statistics not allowing the observation of the small satellite peak, only a single Voigt profile was used for fitting the resonances. Statistical uncertainty obtained from the fit was usually <100 kHz.

Fig. 10

Resonance spectra of the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ transition in $^{12}$Be$^+$ for collinear (left) and anticollinear excitation (right) plotted as a function of the Doppler-tuning frequency. In total 180 single scans were summed up for 8 h. The symmetric spectra were fitted with a single Voigt profile (red line). Residua are displayed in the lower trace

Table 4 Transition frequencies $\nu _0$ for the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{1/2}$ (D1) and the $2s\,^2{\text{S}}_{1/2} \rightarrow 2p\,^2{\text{P}}_{3/2}$ (D2) transition in beryllium isotopes obtained in Run I (Beam time 2008) and Run II (Beam time 2010)

5.5 Transition frequencies

Each pair of spectra was fitted as discussed in Sec. 5.2 to determine the centers of gravity and to extract the respective rest-frame transition frequency $\nu _0$ according to Eq. (9). For each isotope and beam time the weighted mean of all measurements was calculated, and results are listed in Table 4. All transition frequencies from both beam times agree within their $\text{1-}\sigma$ error bars confirming the reproducibility of the measurement. There is a small change compared to Table I of [3], namely a slightly larger uncertainty for $^{10}$Be from Run II in the D2 line due to a transfer error in the statistical uncertainty. Statistical uncertainties in Run II are based on the standard error of the mean for typically 4–5 measurements for $^{11,12}$Be and 20–30 measurements for the less exotic isotopes $^{9,10}$Be. Where available, values from both runs are combined weighted with the respective uncertainty. Systematic uncertainties from the second run cannot be further reduced. While our $^7$Be D2 transition frequency is in very good agreement with the value reported in [31], the frequencies of $^{9}$Be and $^{10}$Be differ by approximately $7\sigma$ and $3\sigma$, respectively, from our results, which are 1–2 orders of magnitude more precise. In particular, the large discrepancy of the ⁹Be value is surprising since this has been obtained in [31] from laser-cooled ions in the Paul trap, whereas the other two isotopes were measured with buffer-gas cooled ions exhibiting line widths of approximately 2 GHz. It seems that the systematic uncertainties of the trap measurements were underestimated in both cases. The transition frequencies can now be used to evaluate differential observables, like the isotope shift, the fine-structure splitting and the splitting isotope shift.

Table 5 Compilation of experimental isotope shifts $\delta \nu _{IS}^{9,A}$ obtained from the transition frequencies $\nu _0$ in Table 4, field shift $\delta \nu _{\text{FS}}$ extracted as the difference to the theoretical mass shifts listed in Table 1 [41] and the corresponding change in the mean-square nuclear charge radius $\delta \left\langle r^2 \right\rangle$ according to Eq. (3)

5.6 Isotope shifts and nuclear charge radii

Isotope shifts are easily obtained as difference of the transition frequency of the isotope of interest and the reference isotope, which in our case is the stable isotope ⁹Be. The field shift $\delta \nu _{\text{FS}}$, also known as the finite nuclear size or nuclear volume effect, can then be extracted according to Eq. (1). The corresponding mass shifts $\delta \nu _{\text{MS}}^{9,A}$ as well as the field shift constant $F^{9,A}$ were theoretically evaluated to an accuracy that exceeds the experimental uncertainty by about an order of magnitude and are compiled in Table 1. We have been using the results from [41, 67] to calculate $\delta \nu _{\text{FS}}$, which is then combined with the reference radius $R_{\text{c}} = 2.519(12)$ fm [43] of ⁹Be to provide total charge radii along the chain using Eq. (4). It should be noted that the uncertainty of $R_{\text{c}}(^9{\text{Be}})$ is probably underestimated since C2 scattering from the quadrupole distribution has been omitted, which might change the radius by about 3% [72].

The results are listed in Table 5. Changes in the mean-square charge radii deduced from the isotope shifts in the D1- and D2-transition are of similar accuracy in case of even isotopes, while for odd-mass isotopes the unresolved hyperfine splitting in the D2 lines leads to larger uncertainties. Figure 11 depicts the development of the rms charge radius along the isotopic chain as extracted from the experiment ($\bullet$) by combining all available data. We have also included results from Fermionic Molecular Dynamics (FMD) calculations [2] that follow the observed trend quite closely, but the charge radii are generally somewhat too small. The two triangles shown for $^{12}$Be are results of two additional calculations performed under the assumption that the two outermost neutrons occupy either a pure $p^2$ state ($\bigtriangledown$), as expected in the traditional shell model or a pure $(sd)^2$ state ($\bigtriangleup$). The latter is expected to contribute to the ground state only if the $N=8$ shell gap between the p shell and the sd shell is significantly reduced. This prediction shows that the charge radius of $^{12}$Be is extremely sensitive to the admixture of sd shell states to the ground state, which was a strong motivation for the measurement of the $^{12}$Be isotope shift.

Fig. 11

Nuclear charge radii along the beryllium isotopic chain. The reference radius of $^{9}$Be was determined from electron scattering experiments [43]. The red bullets ($\bullet$) represent the experimental results with uncertainties dominated by the uncertainty of the reference charge radius of $^{9}$Be. Therefore, all uncertainties are similar in size. Additionally shown are results of Fermionic Molecular Dynamic (FMD) calculations [2]. For $^{10}$Be, calculations were also performed forcing the neutrons into a $p^2$ and an $(sd)^2$ orbit. The bottom row shows the structure of the isotopes interpreted in a cluster picture. For details see text

The trend of the charge radii along the isotopic chain can be understood in a simplified picture based on the cluster structure of light nuclei [64]. This is visualized in the small panels below the graph in Fig. 11. $^7$Be can be thought of as a two-body cluster consisting of an $\alpha$ particle and a helion (pnp = $^3$He) nucleus that are bound together and exhibit a considerable center-of-mass motion. This motion blurs the proton distribution and leads to an increased charge radius. $^8$Be is missing since the two $\alpha$ particles constituting this nucleus are not bound and the nucleus only exists as a resonance. The stable isotope ⁹Be, which has a $\alpha +\alpha +n$ structure, is more compact than $^7$Be because the $\alpha$ particles themselves are very compact and well bound by the additional neutron. This effect is even enhanced with the second neutron added in $^{10}$Be. The sudden upward trend to $^{11}$Be is attributed to the one-neutron halo character of $^{11}$Be which can be disentangled into a $^{10}$Be core and a loosely bound neutron. This halo character not only increases the matter radius, but also affects the charge radius due to the center-of-mass motion of the core caused by the halo neutron. The fact that the charge radius of $^{12}$Be is even larger has been related to the fact that the two outermost neutrons exhibit a strongly mixed sd character rather than belonging to the p shell as expected in the simplified shell-model picture. This mixture leads to an increased probability density outside the $^{10}$Be core, pulling the $\alpha$ particle apart due to the attractive $n-\alpha$ interaction. Theory predicts an $(sd)^2$ admixture of about 70% for this nucleus, being a clear indication for the disappearance of the classical $N=8$ shell closure. For a more detailed discussion of the nuclear charge radii, the comparison with ab initio microscopic nuclear structure calculations and the conclusions about the shell closure see Refs. [1, 2, 65].

Table 6 Fine-structure splittings $\Delta \nu _{\text{fs}}$, the experimental and theoretical [67] splitting isotope shifts $\delta \nu _{\text{sis}}$, and the transferred fine-structure splittings $\Delta \nu _{\text{fs},^A{\text{Be}}\rightarrow \,^9{\text{Be}}}$ for ⁹Be based on the measured splittings in the radioactive isotopes according to Eq. (18) are listed

5.7 Fine-structure splitting and splitting isotope shifts

From the information provided in Table 4 we can furthermore extract the fine-structure splitting as a function of the atomic number. The splitting has previously been measured for ⁹Be with a relative uncertainty of about $3 \cdot 10^{-4}$ [66]. The present value obtained simply from the difference in $\nu _{\text{D1}}$ and $\nu _{\text{D2}}$ of this isotope is already 40 times more accurate although its accuracy is limited by the unresolved hyperfine structure in the D2 transition. Only recently the fine-structure splitting in three-electron atoms became calculable with high precision as demonstrated for the case of lithium [34]. Our result confirmed first calculations for the $Z=4$ three-electron system of Be$^+$ [3]. Moreover, the change in the fine-structure splitting along the chain of isotopes provides a useful check of the so-called splitting isotope shift which can be calculated theoretically to very high accuracy, because the value is nearly independent of both QED and nuclear volume effects. This mass dependence is shown in Fig. 12: The blue data points represent the experimental fine-structure splittings and the red line with red crosses the theoretically expected mass dependence based on the calculated splitting isotope shift and the measured splitting of ⁹Be. The excellent agreement between the theoretical curve and the experimental data can be interpreted as a reliable check of the consistency of the mass shift calculations. On the other hand, it proves the consistency of the experimental data, because the fine-structure splittings are based on the combination of transition frequencies obtained independently in two beam times, even with independent optimization of the experimental conditions. The observation that the data points scatter much less than expected from their error bars can be ascribed to the fact that our systematic uncertainties largely cancel out in considering differential effects.

Fig. 12

Left: Mass dependence of the fine-structure splitting along the beryllium isotopic chain. The red curve with crosses shows the theoretically expected mass dependence—the splitting isotope shift (sis)—with respect to ⁹Be. The experimental values (blue circles) and the sis-corrected values according to Eq. (18) (magenta dots) are included. The solid and dotted lines represent the mean and standard deviation of the corrected values, respectively. Right: Fine-structure splitting in ⁹Be from experiment (line) and theory (data point)

The fine-structure splitting can most reliably be determined for the even–even isotopes $^{10}$Be and $^{12}$Be since there is no hyperfine structure which in the D2 transition obscures the determination of the center of gravity. This is clearly visible in Fig. 12 where the error bars are smallest for these two cases. For these isotopes, the fine-structure splitting was determined sequentially in a short-time interval and therefore the best cancellation of all systematic uncertainties should occur. Indeed, the splitting isotope shift between the two isotopes $\delta \nu _{\text{sis}}^{10,12}=3.43(78)$ MHz agrees very well with the theoretical value of 3.203 MHz. Here the uncertainty of the experimental value is purely statistical assuming that all dominant systematic contributions are cancelled out.

With the confidence gained about the reliability of the theoretical estimates, we can combine the calculated splitting isotope shifts of all isotopes to extract an improved value for the fine-structure splitting of ⁹Be. To this aim, we correct all measured fine-structure splittings by subtracting the theoretical splitting isotope shift

$$\Delta \nu _{\text{fs},{^A\text{Be}}\rightarrow \,^9{\text{Be}}} = \Delta \nu _{\text{fs}}(^A{\text{Be}}) - \delta \nu ^{A,9}_{\text{sis, Theory}}.$$

(18)

The results are included in Table 6 and plotted in Fig. 12 as magenta bullets. The weighted mean for the “isotope-projected” fine-structure splitting of ⁹Be represented by the horizontal line is 197 063.47 (53) MHz. The uncertainty is shown by the dashed lines. We believe that a small remaining systematic uncertainty of the fine-structure splitting is still covered by the size of this uncertainty. In the right hand part of the figure, the theoretical prediction represented by the filled red triangle is compared with experiment. The calculated splitting in ⁹Be amounts to 197 068.0 (25) MHz, which is about 4.5 MHz larger than the experimental value. This difference corresponds to about $1.5\,\sigma$ of the combined uncertainties. The theoretical uncertainty is based on an estimation of the size of the uncalculated nonlogarithmic terms in $m\alpha ^7$. These terms are expected to be <50% of the calculated leading logarithmic terms. To further test the QED calculations in lithium-like light systems, similar measurements on ions with higher Z, e.g., in boron B$^{2+}$ or carbon C$^{3+}$ are of great interest. At least for B$^{2+}$ the wavelength of about 206 nm is still achievable, and measurements with the collinear laser spectroscopy technique presented here are planned.

6 Summary

We have demonstrated that quasi-simultaneous collinear–anticollinear laser spectroscopy on stable and radioactive isotopes can be used to perform precision measurements from which nuclear charge radii even of light and very short-lived species can be extracted. At the same time the data can be used to perform high-precision tests of fundamental atomic structure calculations and bound-state QED. The experimental technique relies on the accurate determination of the laser frequency, which has become possible with the invention and availability of frequency combs. We will apply the technique for further studies: An important case is the determination of the charge radius of the proton-halo candidate $^8$B for which an experiment is currently under preparation at the ATLAS facility at the Argonne National Laboratory.