Bose–Einstein condensates in an optical cavity with sub-recoil bandwidth

Abstract

This article provides a brief synopsis of our recent work on the interaction of Bose–Einstein condensates with the light field inside an optical cavity exhibiting a bandwidth on the order of the recoil frequency. Three different coupling scenarios are discussed giving rise to different physical phenomena at the borderline between the fields of quantum optics and many-body physics. This includes sub-recoil opto-mechanical cooling, cavity-controlled matter wave superradiance and the emergence of a superradiant superfluid or a superradiant Mott insulating many-body phase in a self-organized intra-cavity optical lattice with retarded infinite range interactions.

1 Introduction

Experimental progress in coupling single atoms to single-mode electromagnetic radiation in a cavity has prepared the ground for the field of cavity quantum electrodynamics during the 1980s and 1990s [1, 2]. The focus has since changed toward macroscopic objects, e.g., submicron mechanical oscillators like cantilevers or membranes [3, 4], superconducting qubits [5], quantum dots [6], or droplets of quantum degenerate atomic gases [7], as in the work described in this article. The fragile nature of ultracold quantum ensembles limits one to dispersive light–matter interactions excluding near-resonant excitations followed by spontaneous emission. Hence, the cavity should be pumped by radiation, which is far detuned from any atomic resonance, such that Rayleigh scattering prevails. The first experiments, exploring this regime with optical cavities and laser-cooled thermal atomic samples [8–12] or Bose–Einstein condensates (BECs) [13], have used ring geometries. The use of extreme values of the cavity finesse exceeding several $10^5$ constrains scattering of photons to the modes resonant with the cavity, owing to the Purcell effect [14, 15]. At the same time, this allows one to access the most interesting regime of strong cooperative coupling, when the atom sample acts to shift the cavity transmission resonance by more than its linewidth, and hence, the back-action of the atoms on the intra-cavity light field is significant [10, 12, 16–20].

In addition, an important aspect of the work discussed here is the combination of a high finesse with a large cavity length, yielding the regime of sub-recoil resolution, for which the cavity linewidth is comparable to or smaller than the single-photon recoil frequency, which corresponds to the kinetic energy transferred to a resting atom by backscattering of a single photon. This circumstance has two important consequences. On a single atom level, a photon scattering blockade scenario arises: A first single-photon scattering process drives an atom out of resonance for a subsequent second cavity-assisted scattering process. On a many-body level, the time scale for the evolution of the matter degrees of freedom, i.e., the recoil time, is comparable to the time scale for the evolution of the cavity field, i.e., the photon life time in the cavity. For short cavities with MHz bandwidth (for example, as in Refs. [17–20]), the cavity light field can be adiabatically eliminated such that its net effect on the atoms is described in terms of an instantaneous long-range interaction, while for long cavities, as considered here, the induced long-range interaction has a finite propagation time.

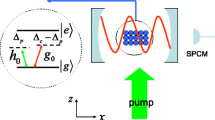
The perhaps most elementary atom–cavity configuration is a BEC interacting with a single longitudinal mode of a standing wave resonator, which is coupled by an external pump field using one of the three elementary coupling geometries depicted in Fig. 1: (a) The pump field arises from a laser beam axially coupled to the cavity through one of its mirrors; (b) the pump field is due to a laser beam irradiating the BEC perpendicularly with respect to the cavity axis, and (c) the pump field has a standing wave geometry resulting from a retro-reflected laser beam intersecting the BEC perpendicularly with respect to the cavity axis. These coupling geometries give rise to surprisingly different physics. Case (a) is characterized by optical bistability, persistent oscillations and superradiant backscattering instabilities, case (b) leads to matter wave superradiance, and case (c) opens a new arena to investigate physics related to the Dicke model [21, 22] and the famous Dicke–Hepp–Lieb superradiant phase transition [23, 24]. In this brief review, a number of characteristic examples of the physics emerging for the three couplings schemes are revisited. Our synopsis of several studies that spread over a number of original articles is complemented by various unpublished results.

Fig. 1

Alternative coupling geometries for the pump light at frequency $\omega _p$. The BEC and the cavity mode are not drawn to scale. a Axial coupling, b transverse traveling wave coupling, c transverse standing wave coupling

2 BEC preparation and cavity setup

A cigar-shaped BEC with Thomas–Fermi radii (3.1, 3.3, 26.8) μm and $N \approx 10^5$ ${^{87}\mathrm{Rb}}$-atoms, prepared in the upper hyperfine component of the ground state $|{F=2,m_F=2}\rangle$, is confined by 3-cm-sized solenoids arranged to provide a magnetic trap with a nonzero bias field with trap frequencies $\omega { /} 2\pi = (215.6 \times 202.2 \times 25.2)$ Hz [25, 26]. Two oppositely mounted mirrors form a standing wave high finesse cavity integrated into the coil setup with the cavity axis along the direction of gravity. For the best possible mode match between the atomic ensemble and the cavity mode, the weekly confining z-axis of the magnetic trap is aligned with the cavity axis. The cavity has a free spectral range $\Delta \nu _{\mathrm{FSR}} = 3$ GHz, a finesse $\mathcal{F} = 3.44 \times 10^5$, a Purcell factor $\eta _\mathrm{c} = 44$ [14] and a field decay rate $\kappa = 2\pi \times 4.45$ kHz. The BEC is exposed to pump fields arranged as shown in Fig. 1) operating at the wavelength $\lambda = 803$ nm, i.e., at large detuning to the negative side of the principle fluorescence lines of rubidium at 780 and 795 nm. For a uniform atomic sample and left circularly polarized light at 803 nm, the cavity resonance frequency is dispersively shifted with respect to the case of an empty cavity by an amount $\delta _{-} = \frac{1}{2} N_a \, \Delta _{-}$ with an experimentally determined light shift per photon $\Delta _{-} \approx -2\pi \times 0.36$ Hz. With $N_a = 5 \times 10^4$ atoms $\delta _{-} = -2\pi \times 9$ kHz, which amounts to $-2\,\kappa$, i.e., the cavity operates in the regime of strong cooperative coupling. For $\sigma _{+}$-light $\Delta _{+} \approx \,-2\pi \times 0.16$ Hz.

Fig. 2

Basic backscattering processes. The momentum states accessible by backscattering (at multiples of $2\hbar k$) are indicated by disks (orange if initially populated, white if initially unpopulated). a Heating process: The blue detuned ($\omega _{\mathrm{p}} > \omega _{\mathrm{c}}$) pump photons (solid blue arrows) are resonantly backscattered into the empty cavity (dashed gray arrows). The light blue horizontal bar represents the cavity linewidth. b Cooling process: Red detuned ($\omega _{\mathrm{p}} < \omega _{\mathrm{c}}$) pump photons (solid red arrows) are resonantly backscattered into the cavity mode by atoms initially prepared at $\pm 2\hbar k$. c Succession of cooling pulses with decreasing negative detuning $\omega _{\mathrm{p}} - \omega _{\mathrm{c}}$

3 Axial coupling

The unique feature of the cavity in the present work is its field decay rate $\kappa$ on the order of the recoil frequency $\omega _{\mathrm{rec}} \equiv \hbar k^2/2 m$ (where $k \equiv 2\pi /\lambda$ and $m =$ atomic mass). As a consequence, cavity-assisted backscattering can only occur in a narrow resonance window such that only very few motional states are dynamically coupled. This is sketched in Fig. 2 for the simplified case when the possible formation of an intra-cavity optical lattice is neglected, and hence, the atoms are considered as freely moving rather than populating Bloch states. For an atom in the zero-momentum state $|{0}\rangle$ [see (a)], backscattering of a photon requires that the atom receives $2\,\hbar k$ momentum and hence a kinetic energy of $4\,\hbar \omega _{\mathrm{rec}}$. Because of the narrow cavity linewidth [indicated by the blue bar in (a)], this process only becomes possible, if the frequency of the pump photon $\omega _{\mathrm{p}}$ is detuned to the blue side of the cavity resonance $\omega _{\mathrm{c}}$ by $4\omega _{\mathrm{rec}}$. After the photon emitted into the cavity has left, a second backscattering process involving the same atom is not supported by the cavity. Hence, backscattering irreversibly populates the momentum states $|{\pm 2\,\hbar k}\rangle$. Similarly, if initially atoms in the $|{\pm 2\,\hbar k}\rangle$ states are prepared, upon offering photons detuned to the red side of the cavity resonance by $4\,\hbar \omega _{\mathrm{rec}}$ these atoms are transferred back to the zero-momentum state [see (b)]. In (c) it is indicated how by applying a suitable sequence of light pulses, with frequencies approaching the cavity resonance from the red side, it should be possible to cool thermal atoms to less than the recoil temperature, in analogy to conventional Raman cooling, albeit at largely increased atomic densities and without the need of spontaneous photons, such that even quantum degeneracy could be reached [27].

Fig. 3

Resonant momentum transfer. a Intra-cavity power for a 200-μs-long heating pulse with positive detuning $\delta _{\mathrm{eff}}/\kappa = 4$. b Population of momentum classes produced by the pulse in a. c, d correspond to a, b, however, after an additional 200-μs-long cooling pulse with negative detuning $\delta _{\mathrm{eff}}{/}\kappa = -3.1$. The light blue bar indicates a 40-μs-long period with the pump beam blocked

3.1 Recoil selective cavity-assisted scattering

In Ref. [28], the elementary processes, sketched in Fig. 2a, b, are experimentally studied. Examples are shown in Fig. 3. In (a) and (b), after preparation of the BEC in the zero-momentum state $|{0}\rangle$, a (heating) pump pulse of 200-μs duration is applied with positive effective detuning $\delta _{\mathrm{eff}}/\kappa = 4$ (with $\delta _{\mathrm{eff}} \equiv \omega _{\mathrm{p}}-\omega _{\mathrm{c}} - \delta _{-}$). The power transmitted through the cavity (blue trace) recorded in (a), which monitors the intra-cavity lattice depth, shows oscillatory dynamics. Via backscattering by the atoms, pump photons at frequency $\omega _{\mathrm{p}}$ are converted into photons resonant with the cavity, which yields a beat in the transmitted light at the difference frequency. After few cycles, most of the atoms are transferred to an excited motional state composed of the momentum states $|{\pm 2\,\hbar k}\rangle$, which can be seen in (b), where the momentum distribution at the end of the pulse is recorded. This is accomplished by mapping the population of the nth band onto the nth Brillouin zone. In the experiment, the lattice is switched off with moderate speed determined by $\kappa$ and, after a 25-ms ballistic flight, the atomic density distribution is recorded. The plot in (b) shows that after the excitation pulse, both momenta ${\pm } 2\,\hbar k$ are equally populated, while the zero-momentum class is entirely depleted. The grayish background arises because atoms in the different momentum states ($0, {\pm } 2\,\hbar k$) elastically scatter into a continuum of scattering states. While these atoms (up to 60%) remain in the cavity and contribute to the atom–cavity coupling, their dynamics is not captured by a dual-mode description. Note that no atoms with momenta ${\pm }2 n\,\hbar k$ with $n>1$ are observed, which shows that excitations into higher bands by multiple backscattering are in fact suppressed due to the sub-recoil energy resolution of the cavity. In (c) and (d) about 40 μs after termination of the blue detuned excitation pulse discussed in (a) and (b), a red detuned (cooling) pulse of the same duration is applied ($\delta _{\mathrm{eff}}/\kappa = -3.1$), which transfers the atoms back to zero momentum. A detailed study of the axial coupling scenario in Ref. [29] further investigates the superradiant dissipative character of the processes shown in Fig. 3 and discusses the occurrence of limit cycle dynamics and the observation of dispersive optical bistability in cavity transmission spectra.

Fig. 4

a Sketch (not drawn to scale) of a BEC placed inside a standing wave cavity, which is axially pumped at frequency $\omega _p$. A magnetic force is applied along the cavity axis. b Typical data set: The blue thick line shows the intra-cavity intensity [parameterized in terms of the associated (negative) intra-cavity light shift], observed during ca. 600 μs by the photodetector in a for the same BEC in a single experimental run. The red disks (connected by solid red straight line segments for eye guiding) show the positions of the density maxima of the atomic cloud versus the holding time in the lattices. The green triangles show the corresponding center of mass of the atomic cloud. The green solid lines show a calculation for $\delta _{c} = -5.8 \, \kappa$. Each data point requires preparation of a new BEC. For the section of the time axis highlighted by a reddish background, images of the BECs after ballistic expansion are shown associated with the data points

3.2 Opto-mechanical Bloch oscillations

A useful application of the axial coupling scenario is the in-situ monitoring of Bloch oscillations [30, 31]. In optical lattices with their perfect periodic structure, Bloch oscillations can be used as a quantum mechanical force sensor, for example, for precise measurements of the gravitational acceleration. However, the destructive character of the measurement process in previous experimental implementations typically poses notable limitations for the precision of such measurements [32–34]. In Ref. [35], we have explored a nonlinear opto-mechanical scenario consisting of a Bose–Einstein condensate (BEC) performing Bloch oscillations in the intra-cavity lattice formed in an optical cavity strongly coupled to the atoms. We show that back-action of the oscillating atoms on the cavity mode leads to a concomitant oscillation of the intra-cavity lattice depth, which can be non-destructively monitored in the light leaking out of the cavity. Hence, with a single atomic sample, the Bloch oscillation dynamics can be mapped out, while in the case of Bloch oscillations in a conventional optical lattice, each data point requires the preparation of a new atomic cloud. According to theoretical works [36–40], the frequency of our coupled system agrees with the Bloch frequency in a conventional lattice with the same lattice constant. Hence, the use of a cavity-based monitor should help to improve the precision of Bloch oscillation measurements for metrological purposes.

The mechanism leading to an oscillation at the Bloch frequency in the cavity transmission is as follows: In a simplified picture of Bloch oscillation dynamics, the atomic wave packet may be approximated by a Bloch function with a quasi-momentum $q(t) = q_0 + d^{-1} \Omega _B \,t$ linearly increasing in time, which therefore periodically crosses through the first Brillouin zone (FBZ). Here, $\Omega _B \equiv F d / \hbar$ is the Bloch frequency exclusively depending on the size of the force F and the lattice constant d. The associated atomic density oscillates between a nearly constant shape for q values near to the center of the FBZ and a grating commensurate with the intra-cavity light intensity for q values near the edge of the FBZ. As a consequence, the resulting atom–cavity coupling strength oscillates with the frequency $\Omega _B$. This leads to an oscillating shift of the cavity resonance frequency and hence to a periodic change of the in-coupled light intensity, which gives rise to a phase and amplitude modulation of the transmitted light intensity at the frequency $\Omega _B$.

An example of a typical data set, taken from Ref. [35], is shown in Fig. 4 with the details deferred to the figure caption. In this implementation, the number of observable Bloch cycles is limited by an extensive binary collision rate that leads to decoherence and heating. This can be avoided in experiments optimized for a precise determination of the Bloch frequency by adjusting zero scattering length exploiting a Feshbach resonance [37, 41] or by using atoms with a naturally small scattering length like strontium [32].

4 Transverse traveling wave coupling

4.1 Matter wave superradiance

In this section, we discuss a study of the collective nature of Rayleigh scattering by a BEC, when the scattered photons are guided by a high finesse cavity combining a Purcell factor far above unity with extreme energy resolution beyond the single-photon recoil energy [42]. A schematic of the setup is sketched in Fig. 5a. This scenario extends a previous experimental study at MIT of Rayleigh scattering from a BEC in free space [43]. In the MIT work, an elongated BEC was irradiated by a monochromatic off-resonant pump laser beam perpendicularly with respect to its long axis. Above a critical pump intensity, the emission of superradiant light pulses along the long axis of the BEC was observed, while the atoms were collectively scattered into a fan of discrete free-space momentum states. If the BEC is enclosed by a recoil-resolving cavity as in our recent study in Ref. [42], the scattering of atoms into higher momentum states can be precisely controlled via adjustment of the cavity resonance frequency. Via control of the available scattering channels, complex spatially periodic matter states can be synthesized, which preserve the full coherence of the initial condensate. With appropriate pulse sequences, the entire atomic sample can be collectively accelerated or decelerated by multiples of two recoil momenta.

Fig. 5

a Sketch of the scattering geometry. The pump is linearly polarized along the x-axis. b Relevant momentum states coupled to the BEC via scattering of pump photons. The tuples (n, m) below the filled gray disks denote the momenta along the y and z directions in units of $\hbar k$. The numbers above the disks indicate the kinetic energy in units of the recoil energy. The colored numbers on the arrows indicate the kinetic energy transfer associated with the respective scattering process. c The intra-cavity photon number $N_p$ is recorded for variable fixed values of $\delta _{\mathrm{eff}}$, while $\varepsilon _p$ is linearly increased from 0 to 3 in 2 ms. d Mean field calculation of the intra-cavity photon number for the pump strength ramp applied in c. e The blue solid trace shows the intensity leaking out of the cavity, while the pump strength is ramped from zero to $3\,E_{\mathrm{rec}}$ in 2 ms (as indicated by the red dashed trace) with negative detuning $\delta _{\mathrm{eff}}/2\pi = -12$ kHz. The insets numbered 1–6 show (single shot) momentum spectra taken at times marked by the black arrows. The green dashed-dotted line indicates the noise floor of the light detection

As a consequence of the sub-recoil bandwidth, similarly as in the case of axial coupling, only a few selected motional states are coupled. This is sketched in Fig. 5b for the simplified case when the transient formation of an intra-cavity optical lattice and the external trap are neglected, and hence, the atoms are considered as freely moving. Scattering of a pump photon by a BEC atom into the cavity corresponds to a transition from the $(0,0)\,\hbar k$ to the $(1, {\pm }1)\,\hbar k$-momentum states. Energy conservation requires $\omega _p - \omega _{\mathrm{scat}} = 2\,\omega _{\mathrm{rec}}$ with $\omega _p$ and $\omega _{\mathrm{scat}}$ denoting the pump frequency and the frequency of the scattered photon, respectively. The scattering process is best supported by the cavity, if $\omega _{\mathrm{scat}}$ coincides with the effective cavity resonance frequency $\omega _{c,\mathrm{eff}} \equiv \omega _c - \delta _{-}$ with $\delta _{-}$ according to Sec. 2 and $\omega _c$ denoting the resonance frequency of the empty cavity, i.e., the effective detuning $\delta _{\mathrm{eff}} \equiv \omega _p - \omega _{\mathrm{c,eff}}$ should satisfy $\delta _{\mathrm{eff}} = 2\,\omega _{\mathrm{rec}}$. The same detuning allows to resonantly scatter a second photon bringing the atom to the $(2,0)\,\hbar k$ state. Further scattering, which would transfer the entire atomic sample via the $(3, {\pm }1)\,\hbar k$ states to the $(4,0)\,\hbar k$ state, is not supported by the cavity unless $\delta _{\mathrm{eff}}$ is modified to account for the significantly larger energy costs of 6 recoil energies per atom. Due to the back-action of the scattered photons on the atomic sample, the scattering mechanism is expected to acquire collective character leading to the emission of a superradiant light pulse along the cavity axis: If the initial sample, a BEC in the $(0,0)\,\hbar k$ state, was perfectly homogeneous, scattering would be prevented by destructive interference from contributions from different locations within the BEC. Hence, quantum or thermal fluctuations are required to start the scattering process. Once a few photons are scattered into the cavity, the light field building up inside the cavity oscillating at frequency $\omega _p - 2 \omega _{\mathrm{rec}}$ interferes with the pump wave with frequency $\omega _p$. The result is a moving optical potential and a commensurate moving density grating formed by the atoms transferred into the $(1, {\pm }1) \hbar k$-momentum states. This grating acts as a Bragg grating, which enhances the scattering efficiency such that the optical standing wave and the corresponding matter grating grow in an exponential process reaching maximal values, when most atoms populate $(1, {\pm }1) \hbar k$. Their further transfer to $(2,0) \hbar k$ suppresses superradiance again, since in this state, no density grating along the cavity axis can be formed. Hence, scattering terminates and the atoms remain in the state $(2,0) \hbar k$ with no photons in the cavity.

Fig. 6

a The white and gray disks symbolize different momentum states with momenta $(n,m)\,\hbar k$ specified below the gray disks. The colored arrows symbolize different scattering processes in momentum space. The numbers on top of the arrows specify the associated number of recoil energies transferred. b The green solid line shows the detuning of the pump beam. The solid blue line shows the observed intra-cavity intensity. c Momentum spectra recorded at the instances of time indicated by numbers and arrows in b

Figure 5c, d shows a measurement (c) and a calculation (d) of the instability boundary in the plane spanned by the effective pump detuning $\delta _{\mathrm{eff}}$ and the pump strength $\varepsilon _{p}$. In both plots, the pump strength is ramped up from zero to $3\,\omega _{\mathrm{rec}}$ in 2 ms for different settings of $\delta _{\mathrm{eff}}$, and the intra-cavity intensity, is plotted according to the specified color code. The observed and calculated instability boundaries depend on the duration of the $\varepsilon _{p}$-ramp, since the system is unstable in the entire ($\varepsilon _{p}$, $\delta _{\mathrm{eff}}$)-plane, as a linearization of the dynamical equations around the solution of zero intra-cavity intensity and no condensate depletion shows [42]. As expected from Fig. 5b, the most efficient scattering (i.e., scattering for minimal pump strength) arises at about 7 kHz corresponding to $\delta _{\mathrm{eff}} \approx 2\,\omega _{\mathrm{rec}}$, when the $2\,\omega _{\mathrm{rec}}$-process is resonant. In (e) a horizontal section through (c) is analyzed in more detail with momentum spectra recorded at several instances of time. It is seen that a rapid sudden transfer of the BEC to the $(2,0) \hbar k$ momentum state is observed with a superradiant light pulse emitted into the cavity.

4.2 Superradiant atom accelerator

The cavity-assisted steering of the scattering channels may be used for controlled acceleration of a BEC. In order to successively transfer the BEC through the momentum states $(2 n,0)\,\hbar k$ from $n=0$ to $n=5$ (see Fig. 6a), a series of five pump pulses were applied with frequencies adjusted to successively tune the scattering by atoms populating the $(2 n,0)\,\hbar k$ momentum state to resonance. The variation of the pump detuning is recorded as the green solid line in Fig. 6b. The blue solid line shows the superradiant pulses emitted into the cavity enabling the momentum transfer. In Fig. 6c, a series of momentum spectra demonstrate that the entire BEC is in fact accelerated. The total momentum after five scattering pulses, each transferring $2\,\hbar k$ momentum, turns out to be less that $10\,\hbar k$, because the atoms are also decelerated by climbing up the harmonic trap potential.

Fig. 7

a Momentum (upper detail) and energy budget (lower detail). b Subradiant superfluid phase (SubSF): The BEC is trapped in the ground state of the quasi 1D pump lattice, and no light is scattered into the cavity. c Superradiant superfluid phase (SupSF): A 2D optical lattice is formed; the atoms are spatially structured to form a Bragg grating, which optimizes scattering into the cavity. The lower details in b and c show schematics of the expected atomic momentum distributions

5 Transverse standing wave coupling

If the traveling pump wave in Fig. 5a is replaced by a standing wave, surprisingly different physics is encountered. At negative pump detuning $\delta _{\mathrm{eff}}$, beyond a critical pump strength, a stationary self-organized intra-cavity optical lattice can build up. The momentum and energy budget for this process is illustrated in Fig. 7a. Since we operate at negative detuning with respect to the relevant atomic resonances (the case of normal dispersion), the intra-cavity lattice comes with a negative light shift, such that scattering of a pump photon negatively detuned (red arrow in Fig. 7a) with respect to the cavity resonance allows one to reach a bound state in the intra-cavity lattice (indicated by a green bar in the lower detail). The associated self-organization phase transition has been predicted and experimentally demonstrated for thermal atomic samples in Refs. [44, 45], respectively. Later, a similar transition was demonstrated using a BEC [46] and it was emphasized that close to the transition boundary, the system can be approximated by the driven open Dicke model [46–49]. For positive pump detuning (blue arrow in Fig. 7a), bound states in an intra-cavity lattice cannot be reached and hence a stationary intra-cavity lattice is not formed in this regime. Rather, for arbitrarily small pump strength, the system is excited to free-space momentum states in a cascade of pulsed superradiant scattering events, similarly as for any value of $\delta _{\mathrm{eff}}$ in the case of a traveling wave pump, considered in the previous section.

Fig. 8

a Instability exponent plotted versus the effective detuning $\delta _{\mathrm{eff}}$ and the depth of the pump lattice $\varepsilon _p$. b, c show sections through a for $\delta _{\mathrm{eff}}/2\pi = \pm 20$ kHZ. In addition to the instability exponent (red traces), also the excitation energies are plotted (blue traces)

5.1 Superradiant self-organization transition

The self-organization transition at negative $\delta _{\mathrm{eff}}$ may be understood according to Fig. 7b, c. For small pump intensity (b), the atoms are merely trapped in the pancake-like high-intensity regions of the quasi 1D pump lattice along the y-axis, which should lead to a momentum spectrum showing, aside from the dominating zero-momentum condensate peak, further higher-order contributions at multiples of $p_y = \pm 2\,\hbar k$ [as sketched in the lower detail of (b)]. Along the cavity axis (z-axis), a nearly homogeneous density distribution prevails such that, for every atom ready to scatter a photon into the cavity, a second atom can be found, which would scatter with opposite phase, such that destructive interference prevents scattering altogether. As a consequence, no intra-cavity light field arises. This phase is henceforth addressed as subradiant, superfluid (SubSF). Above a critical strength of the pump field, initiated by quantum or thermal fluctuations, an exponential instability occurs and a 2D light field is formed by interference of the pump field and the intra-cavity field, which are both linearly polarized along the x-axis. This is illustrated in Fig. 7c. In the relevant case of normal dispersion, if $|\delta _{\mathrm{eff}}| \gg \kappa$, the intra-cavity field is created in phase with the pump field at the positions of all contributing scatterers. Two distinct position offsets of the resulting optical potential and the associated density grating are possible (separated by $\lambda /2$ along the z-axis). Which of them is actually realized depends on the geometry of the initial density fluctuation. The density grating acts as a Bragg grating, thus giving rise to superradiant scattering and hence a rapid increase of the optical potential, which in turn yields increasing contrast of the density grating. The emergence of this self-organized lattice is indicated by additional Bragg resonances in the momentum spectrum at multiples of $(p_x,p_y) = ({\pm }\hbar k, {\pm }\hbar k)$. Once the optical lattice is formed, the atomic density grating is commensurate with the optical trapping potential, i.e., every available lattice site carries the same average population. For this reason, it appears misleading to call this phase a supersolid or a density wave although its position offset arises via spontaneous breaking of an initial $Z_2$ symmetry. Henceforth, it is denoted as superradiant, superfluid phase (SupSF).

Fig. 9

The stability diagram of Fig. 8 is repeated in a and compared to an observation of the intra-cavity lattice depth in b. Insets show momentum spectra recorded at the positions indicated by a white and a black cross, respectively

5.2 Validity of Dicke model and cavity bandwidth

Close to the critical pump strength, the self-organization phase transition simulates the second-order phase transition expected to occur in the driven open Dicke model [46–49]. This applies in the regime where it is justified to assume a two-mode scenario for the motional states of the atomic matter, i.e., the BEC mode $|0,0\rangle$ and the superposition $\frac{1}{4} \sum _{\nu ,\mu \in \{-1,1\}} |\nu \hbar k,\mu \hbar k\rangle$. In atom–cavity systems with a large cavity bandwidth, the momentum states $|\pm \hbar k,\pm \hbar k\rangle$ are coupled to a multitude of higher-order motional states such that a description in terms of the Dicke Hamiltonian is only justified in the limit of vanishing condensate depletion, i.e., very close to the self-organization phase transition boundary. In case of a narrow cavity bandwidth, due to the scattering blockade effect, the coupling to higher-order momentum states is significantly decreased (but not completely eliminated), and hence, the regime of validity of the Dicke picture is extended. Furthermore, due to the comparable time scales for the evolution of the matter and light degrees of freedom, the system is easily driven away from equilibrium. Hence, the observation of the equilibrium phase transition requires an extremely slow tuning of the pump strength across the critical value in order to remain adiabatic.

5.3 Stability analysis and phase diagram

As is discussed in more detail in Ref. [50], a stability analysis for the SubSF phase, characterized by zero BEC depletion and vanishing intra-cavity field, reveals the different nature of the physical scenarios arising for positive and negative $\delta _{\mathrm{eff}}$. Linearization of the mean field equations of the system in the SubSF phase and analysis of the eigenvalues of the stability matrix lets one determine the rate for an exponential instability of this phase. The instability exponent, which is the rate for exponential departure from the SubSF phase is plotted in Fig. 8a versus the effective detuning $\delta _{\mathrm{eff}}$ and the depth of the pump lattice $\varepsilon _p$. For negative $\delta _{\mathrm{eff}}$, below the critical threshold indicated by the dashed red line, the SubSF phase is a stable solution. Beyond the threshold, this solution is exponentially unstable with an exponent parameterized by a color code in units of $\kappa$. Note the interesting fact that when $\delta _{\mathrm{eff}}$ approaches zero, the SubSF phase remains stable for arbitrarily strong pumping. The reason is as follows: When $|\delta _{\mathrm{eff}}|$ becomes smaller than $\kappa$, the relative phase between the intra-cavity field and the pump field approaches $\pi /2$ as $|\delta _{\mathrm{eff}}| \rightarrow 0$. This suppresses the interference between both fields, i.e., their intensities simply add. As a result, the unit cell develops a second minimum, which approaches equal depth for $\delta _{\mathrm{eff}}\rightarrow 0$. The associated density grating, now composed of atoms trapped in both classes of minima, no longer supports Bragg scattering of pump photons into the cavity, and hence, the intra-cavity field and the density grating collapse. In Fig. 8b, a vertical section through (a) at $\delta _{\mathrm{eff}}/2\pi = -20$ kHz is shown. In addition to the instability exponent (red traces), also the excitation energies are plotted (blue traces). The plot shows that the lowest excitation (of the $2\,E_{\mathrm{rec}}$-mode) undergoes softening when the critical pump strength is approached. An expansion of the vicinity of the critical pump strength shows that there is a small interval of $\varepsilon _p$, where this mode has acquired zero frequency, while the SubSF phase yet remains stable. In contrast, in the case of positive $\delta _{\mathrm{eff}}$, the SubSF phase is everywhere unstable. This is emphasized by the positive red trace in Fig. 8c showing a vertical section through (a) for $\delta _{\mathrm{eff}}/2\pi = 20$ kHz.

In Fig. 9 the stability diagram of Fig. 8, repeated in (a), is compared to observations for the same section of the $(\delta _{\mathrm{eff}},\varepsilon _p$)-plane in (b). In (b) the intra-cavity lattice depth (parameterized by the indicated color scheme) is recorded while ramping up $\varepsilon _p$ in 10 ms from zero to $26\,E_{\mathrm{rec}}$ for different settings of $\delta _{\mathrm{eff}}$. In the half-plane of negative $\delta _{\mathrm{eff}}$ a stationary intra-cavity lattice is observed above a critical value of $\varepsilon _p$, slightly larger than the predicted second-order equilibrium phase boundary indicated by the dashed red line in (a). A momentum spectrum recorded at the position indicated by the white cross shows distinct Bragg peaks as expected for a coherent stationary 2D optical square lattice. In the positive $\delta _{\mathrm{eff}}$ half-plane, no stationary lattice arises. Rather, when the contour of the instability exponent indicated by the red dashed line in (a) is crossed, a short intense spike of light is emitted into the cavity, and the system becomes irreversibly excited. This is exemplified by the momentum spectrum recorded at the position indicated by the black cross, which shows a nearly complete depletion of the condensate peak. The emission of superradiant light pulses observed for positive $\delta _{\mathrm{eff}}$ reflects the same physics of matter wave superradiance found to occur at any value of $\delta _{\mathrm{eff}}$ in the case of traveling wave coupling, discussed in Sec. 4.

Fig. 10

a For fixed $\delta _{\mathrm{eff}} = - 2 \pi \times 17.5$ kHz the intra-cavity intensity is plotted with the pump strength ramped from 0 to $4\,E_{\mathrm{rec}}$ in 1.5 ms (blue line) and back (red line). Below a, a series of consecutively numbered momentum spectra are shown (1–5), recorded at increasing times during the $\varepsilon _p$-ramp, indicated by the correspondingly numbered arrows in a. b A mean field calculation according to a for a homogeneous, infinite system without collisional interaction. In c mean field calculations of $\varepsilon _{p,1}$ (lower graph, red dots) and $\varepsilon _{p,2}$ (upper graph, blue dots) are shown. The solid lines show power laws with exponents $n_1=-0.57$ and $n_2=-0.85$ in the lower and upper graph, respectively. The measured dependence of the critical values $\varepsilon _{p,\mu }, \mu \in \{1,2\}$ upon the quench time $\tau _Q$ is shown for $\mu =2$ in d and for $\mu =1$ in e. The solid lines repeat the power laws found in the mean field calculations in c. The error bars reflect the standard deviations for 10 measurements

5.4 Quench across phase boundary, hysteresis

A more complete picture of the physics encountered for negative $\delta _{\mathrm{eff}}$ is provided in Fig. 10, where the transition through the phase boundary is studied for $\delta _{\mathrm{eff}} = - 2 \pi \times 17.5$ kHz in more detail. In (a) $\varepsilon _p$ is ramped up from 0 to 4 in 1.5 ms and back to 0 again in 1.5 ms. The solid blue and red lines show the observed intra-cavity intensity for the increasing and decreasing sections of the ramp, respectively. Note that this quantity measures the depth of the intra-cavity lattice emerging in the SupSF phase and hence corresponds to the square of the order parameter for the Dicke phase transition. A significant hysteresis is observed. For increasing $\varepsilon _p$, a sudden jump of the intra-cavity intensity arises on a time scale corresponding to the cavity decay rate. On the way back, the intra-cavity intensity is smoothly tuned to zero. In the center row of the figure [below (a) and (b)], a series of consecutively numbered momentum spectra are shown, recorded at different instances of time during the $\varepsilon _p$-ramp, indicated by the correspondingly numbered arrows in (a). As the intra-cavity intensity assumes finite values, a coherent optical lattice is formed (arrow 2), as is seen from the occurrence of higher-order Bragg peaks. As the lattice depth grows (arrows 3 and 4), tunneling amplitudes decrease, and the relatively increased collisional interaction acts to reduce particle number fluctuations resulting in a partial loss of coherence. When ramping back to small values of $\varepsilon _p$, the BEC is recovered with no notable atom loss and only few low-energy Bogoliubov excitations (arrow 5).

In Fig. 10b a mean field calculation is shown for a homogeneous, infinite system without collisional interaction, which shows the same signatures as observed in (a) including dynamical details as the oscillation of the red trace around $\varepsilon _p \approx 2.5$ and the overshooting of the blue trace around $\varepsilon _p \approx 3.5$. The observed hysteresis appears fundamentally different from that known to occur in conventional bistable systems, where discontinuities arise for both critical values, where the system becomes unstable. We do not find a discontinuity at the lower critical value $\varepsilon _{p,1}$ in Fig. 10a, b; however, the system always follows the blue curve, when this point is passed with increasing $\varepsilon _p$, irrespective of the duration $\tau _Q$ of the applied $\varepsilon _p$-ramp. For increasing cavity bandwidths, our mean field calculations predict that the area enclosed by the hysteresis decreases and finally is obscured by increasing opto-mechanical oscillations at the phase boundary.

Fig. 11

Kibble–Zurek scenario: $t(\varepsilon _{p})$ denotes the time elapsed during ramping from $\varepsilon _{p,c}$ to $\varepsilon _{p}$ and $\tau _{\mu }(\varepsilon _{p}), \mu \in \{1,2\}$ denote the relaxation times of the system

5.5 Power law behavior

The dependence of the threshold values $\varepsilon _{p,1}$ and $\varepsilon _{p,2}$ for the dynamical transitions in Fig. 10a, b upon the quench time $\tau _Q$ is studied in (c)–(e). These quantities are determined as those values of $\varepsilon _p$, where the intra-cavity intensity assumes 5% of its maximal value reached for $\varepsilon _p = 4$. In (c) the values of $\Delta \varepsilon _{p,\mu }(\tau _Q)\equiv \varepsilon _{p,\mu }(\tau _Q) - \varepsilon _{p,\mu }(\tau _Q=\infty )$ ($\mu \in \{1,2\}$), calculated from curves as that shown in (b), are plotted versus $\tau _Q$. As shown by the solid lines, the $\tau _Q$-dependences follow power laws $\Delta \varepsilon _{p,{\mu }}(\tau _Q) \propto {\tau _Q}^{n_{\mu }}$ with $n_1=-0.57$ and $n_2=-0.85$. The phase offset of the sharp resonances occurring periodically at a frequency $\Omega = 0.682\, \omega _{\mathrm{rec}}$ in the upper graph depends on the specific choice of a small initial excitation, necessary to drive the system out of the SubSF phase, which is provided by quantum and thermal fluctuations in the experiment. The exponents $n_1, n_2$ turn out independent of the exact initial conditions (for details see Ref. [50]). In (d) and (e) we plot the experimentally observed values of $\Delta \varepsilon _{p,\mu }(\tau _Q)$ with $\mu =2$ and $\mu =1$, respectively. The solid lines repeat the power laws found in the calculations in (c) with $n_2=-0.85$ in (d) and $n_1=-0.57$ in (e). While in (d) the data nicely agree with the power law behavior, in (e) this is only the case for the first half of the plot. At later times, the data points assume an exponential rather than a power law decay, which is in accordance with the observation that for long ramp times at the end of the descending ramp, notable particle loss sets in.

5.6 Kibble–Zurek picture

The fact that the observed intra-cavity intensity is a direct measure of the order parameter together with the observations of power law behavior of $\Delta \varepsilon _{p,\mu }(\tau _Q)$ suggests an interpretation within the universal model introduced by Kibble and Zurek [51–53], which applies for second-order phase transitions in isolated many-body systems. According to this model, a quench between two phases is approximated by a succession of an adiabatic approach toward and a departure from the equilibrium critical point $\varepsilon _{p,c}$ conjoined by a diabatic passage through the critical point, where the dynamics is completely frozen (c.f. Fig. 11). The time $t(\varepsilon _{p})$ elapsing during the $\varepsilon _{p}$ ramp after passing $\varepsilon _{p,c}$ may be parameterized as $t(\varepsilon _{p}) = \frac{\varepsilon _{p} - \varepsilon _{p,c}}{\varepsilon _{p,2} - \varepsilon _{p,1}}\,\tau _Q$ with the quench time $\tau _Q$. Furthermore, a power law dependence for the relaxation time is assumed, i.e., $\tau _{\mu }(\varepsilon _{p}) \propto |\varepsilon _{p}-\varepsilon _{p,c}|^{-z_{\mu } \nu _{\mu }}$ with $\mu \in \{1,2\}$ if $\varepsilon _{p}<\varepsilon _{p,c}$ and $\varepsilon _{p}>\varepsilon _{p,c}$, respectively. The identification of $\Delta \varepsilon _{p,\mu }$ with the lower and upper bounds of the diabatic region around $\varepsilon _{p,c}$ (i.e., $|t(\varepsilon _{p,\mu })| = \tau _{\mu }(\varepsilon _{p,\mu })$) then leads to the prediction that $z_{\mu } \nu _{\mu }= -(1 + \frac{1}{n_{\mu }})$, i.e., in our system: $z_{1} \nu _{1} = 0.75$, $z_{2} \nu _{2} = 0.18$ (for details, see the supplement of Ref. [50]). A physical understanding of these values would require a comprehensive extension of the concept of universality to the case of driven open systems [54], which is a topic of intensive ongoing research.

Fig. 12

Plots analogous to Fig. 9b, however, with the intensity of the retro-reflected pump wave (cf. Fig. 1c) reduced to a fraction $\zeta$. The vertical dashed red lines emphasize $\delta _{\mathrm{eff}} = 0$. The curved dashed red lines emphasize the instability boundary for matter wave superradiance

5.7 Crossover between standing wave and traveling wave coupling

The striking difference of the physics observed for transverse traveling wave and transverse standing wave coupling gives rise to the question, how these two regimes are connected. Experimentally, it is easy to gradually decrease the intensity in the retro-reflected pump wave in Fig. 1c, such that the two coupling scenarios are smoothly transferred into one another. In Fig. 12, this crossover is illustrated by showing the phase diagram, recorded similarly as in Fig. 9b, for different fractions of the retro-reflected intensity $\zeta = 1, 0.25, 0.15, 0$. The plots clearly show how the SupSF phase pulls back toward larger values of $\varepsilon _{p}$ and increasingly negative values of $\delta _{\mathrm{eff}}$ as $\zeta$ approaches zero, while the regime of matter wave superradiance progressively extends into the half-lane of negative detuning.

Fig. 13

a The intra-cavity photon number is plotted versus $\delta _{\mathrm{eff}}$ and $\varepsilon _p$. The SubSF–SupSF phase boundary is highlighted by a thick dashed–dotted black line. Six locations in the phase diagram are highlighted by capital letters A–F. Three trajectories $\overline{\mathrm{ABCD}}$, $\overline{\mathrm{DCD}}$ and $\overline{\mathrm{EFE}}$ are indicated along which the degree of coherence of the atomic sample is observed. The black squares labeled by Greek letters $\alpha , \beta , \gamma$ show the observed boundary between the SupSF and the SupMI phase. b The upper panel quantifies the tuning of $\delta _{\mathrm{eff}}$ (black squares) and $\varepsilon _p$ (green disks) along the path $\overline{\mathrm{ABCD}}$ in a. In the lower panel, the intra-cavity photon number $N_p$ (red disks) and the width (FWHM) $\mathcal{W}$ of the observed zero-momentum Bragg resonance (blue diamonds) with regard to the z-direction are plotted. The red and blue solid lines are linear fits including the data points highlighted by black margins. The red dashed line corresponds to the white delimited data points. The SubSF–SupSF and the SupSF–SupMI phase boundaries are defined by the intersections of the red and blue lines with the $(N_p = 0)$- and $(\mathcal{W} = 1)$-lines, respectively. In c momentum spectra (in the ($k_y, k_z$)-plane) are shown recorded at the locations on the path $\overline{\mathrm{ABCD}}$ indicated by the black arrows in b

5.8 Superradiant Mott insulator

Theoretical work [55, 56] has suggested that the SupSF phase discussed above should have a Mott insulating counterpart, if contact interaction dominates tunneling, similarly as found in conventional optical lattices simulating the bosonic Hubbard model [57]. To enter this regime, tight confinement is required along all spatial directions. In this subsection, we consider the setup of Fig. 1c extended by an additional standing wave oriented perpendicularly with respect to the drawing plan in Fig. 1c (i.e., parallel to the x-axis), which has been studied in Ref. [58]. An even further extended scenario with a second external lattice along the cavity axis (z-axis in Fig. 1c) has been reported in Ref. [59]. The polarization of the additional light field applied in Ref. [58] points along the cavity axis (z-axis) such that it cannot give rise to light scattering into the cavity and hence its only effect is to provide an additional periodic potential. The depth of the resulting lattice is adjusted to $14\, E_{\mathrm{rec}}$ such that tunneling is suppressed along the x-axis. As a consequence, in addition to the SupSF phase entered upon tuning the pump strength above a critical value, a further increase of the pump strength above a second critical value leads to a sudden complete loss of coherence in time-of-flight spectra, indicating the emergence of a self-organized superradiant Mott insulating phase (SupMI). By successively traversing the phase boundary in both directions, it is found that coherence is restored as the SupSF phase is reentered. This shows that the loss of coherence observed in the SupMI region cannot be attributed to irreversible heating.

By tuning $\delta _{\mathrm{eff}}$ and $\varepsilon _p$ we drive the system along the three trajectories $\overline{\mathrm{ABCD}}$, $\overline{\mathrm{DCD}}$ and $\overline{\mathrm{EFE}}$ that intersect the SubSF, SupSF and SubMI phases in different regions of the ($\delta _{\mathrm{eff}}$, $\varepsilon _p$)-plane, connecting locations labeled by the capital letters A–F in Fig. 13a. Along these trajectories, in addition to the intra-cavity photon number, momentum spectra are recorded. Evaluating the widths of the Bragg resonances in these spectra, we obtain information on the degree of phase coherence of the sample along the trajectory. The exemplary case of the path $\overline{\mathrm{ABCD}}$, which is traversed in 12 ms, is detailed in Fig. 13b. The upper panel shows how $\delta _{\mathrm{eff}}$ and $\varepsilon _p$ are changed versus time, thus successively passing the points “A–D.” In the lower panel, the intra-cavity photon number $N_p$ (red disks) and the width (FWHM) $\mathcal{W}$ of the observed zero-momentum Bragg resonance (blue diamonds) with regard to the z-direction are plotted. A reference momentum spectrum for $\varepsilon _p=0$ is shown in Fig. 13c, labeled “1.” Due to technical reasons detailed in Ref. [58], as the pump strength is raised to $5\,E_{\mathrm{rec}}$ without a notable intra-cavity photon number yet arising, $\mathcal{W}$ slightly decreases. We thus have chosen “B” as the reference point for $\mathcal{W}$, setting $\mathcal{W}(B)=1$. Shortly past point “B,” the transition into the SupSF phase is observed indicated by the sudden increase of the intra-cavity photon number. The width of the zero-momentum Bragg peak practically maintains its reference value of unity, which indicates complete coherence, until point “$\beta$” is reached. This is supported by the two exemplary momentum spectra shown for this section in Fig. 13c, labeled “2” and “3.” These spectra show increasing population of higher-order Bragg peaks. In “2” the $({\pm }2, 0)\, \hbar k$ Bragg peaks become visible, which result from the $5\,E_{\mathrm{rec}}$ deep pump lattice. The intra-cavity contribution to the overall lattice potential is yet negligible. In “3” the visibility of the $(\pm 1, \pm 1)\, \hbar k$ peaks results from the presence of a notable intra-cavity photon number of $5.6\times 10^3$, which yields an overall lattice potential with a well depth of 5.8 $E_{\mathrm{rec}}$ with respect to the plane spanned by the cavity and the pump wave. Only when the point “$\beta$” is passed, which corresponds to an intra-cavity photon number $8.2\times 10^3$ and 8.0 $E_{\mathrm{rec}}$ well depth, a sudden more than tenfold increase of $\mathcal{W}$ is encountered. At this point, a kink in the dependence of $N_p$ upon $\delta _{\mathrm{eff}}$ appears, indicating an increase of the superradiant scattering efficiency due to reduced particle number fluctuations [60]. At point “C” coherence is completely lost as is also directly seen in the momentum spectrum “4” in Fig. 13c. In the subsequent section $\overline{\mathrm{CD}}$ the pump strength is reduced again to zero and $\mathcal{W}$ is observed to decrease again, finally reaching nearly the value initially prepared at point “A.” The significant recovery of coherence indicates that its loss at large lattice depths is not a consequence of excessive heating, but rather indicates the emergence of the SupMI state. The particle number $N_a$ at point “D” is reduced to 60% of the initial number at point “A.” As is detailed in Ref. [58] we attribute this to three-body loss associated with the large peak density in the initial BEC. Without the additional external lattice, the observed particle loss is only on the 1% level [58].

6 Conclusion

Quantum gases subjected to high finesse optical cavities provide a rich experimental platform to explore phenomena at the boundary between many-body physics and quantum optics. Atom–cavity setups are particularly suited to study driven open systems far from equilibrium. Here, we have discussed examples such as recoil-resolved cavity-assisted scattering, opto-mechanical Bloch oscillations, cavity-controlled matter wave superradiance, the emergence of a superradiant superfluid and a superradiant Mott insulating many-body phase in a self-organized intra-cavity optical lattice with retarded infinite range interactions. The present article takes a very limited perspective, exclusively focussing on recent studies in Hamburg. Readers with an interest in a broader viewpoint may wish to consider a more extended review article, e.g., Ref. [7]. However, the field of atom–cavity physics is still rapidly growing such that a complete overview of the present state of the art requires to consult the original literature.